滑块碰撞次数与圆周率π的联系

李开玮

(广东理工学院,广东 肇庆 526100)

图1 问题示意图

1 问题提出

如图1所示,水平光滑的地面上放置小木块m,大木块M,左端是固定的墙壁,初始时刻m静止,M以初速度v0向左运动,将与m发生碰撞,之后m获得速度向左运动,将与墙壁发生碰撞反弹,设所有碰撞均没有动能损失,求碰撞次数．

解析:首先分析最简单情况,若两滑块质量相等m=M,则M向左运动第1次与m碰撞,根据动量守恒和能量守恒,大木块将把速度传递给小木块,而自身静止,m将以v0向左运动,直至与墙壁第2次碰撞,速度反向向右,大小不变,之后向右运动,与M第3次碰撞,同样的道理,碰撞后,m停止,M以v0向右运动．碰撞次数一共为3.

若M≠m呢,总碰撞次数将是多少?接下来利用速度相空间法跟踪两滑块碰撞过程,求解出碰撞次数．

2 速度相空间法

当两滑块质量不相等时,设M/m=k,以水平向右为正方向,设第n次碰撞后,m与M速度分别为un和vn,初始速度即为0和v0,当m与M速度向右,且m速率小于等于M速率时,碰撞结束,若第n次碰撞为两滑块间碰撞,则根据动量守恒、能量守恒有

mun+Mvn=mun-1+Mvn-1，

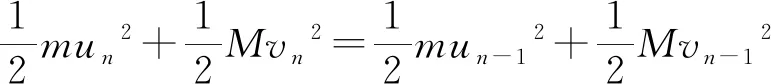
将两滑块碰撞前后速度用矩阵运算表示可得

(1)

若第n次碰撞为小滑块与墙壁间碰撞,则小木块速度反向,大木块速度不变,表示成矩阵运算为

(2)

利用(1)、(2)迭代运算及碰撞结束时的限制条件,可以编写计算程序,统计出碰撞次数,作者也编写了一个MATLAB程序用于计算碰撞次数,代码如图2所示．计算结果如表1所示,通过计算数据可以发现碰撞次数与π的联系．

图2 MATLAB代码

表1 碰撞次数随着k的变化

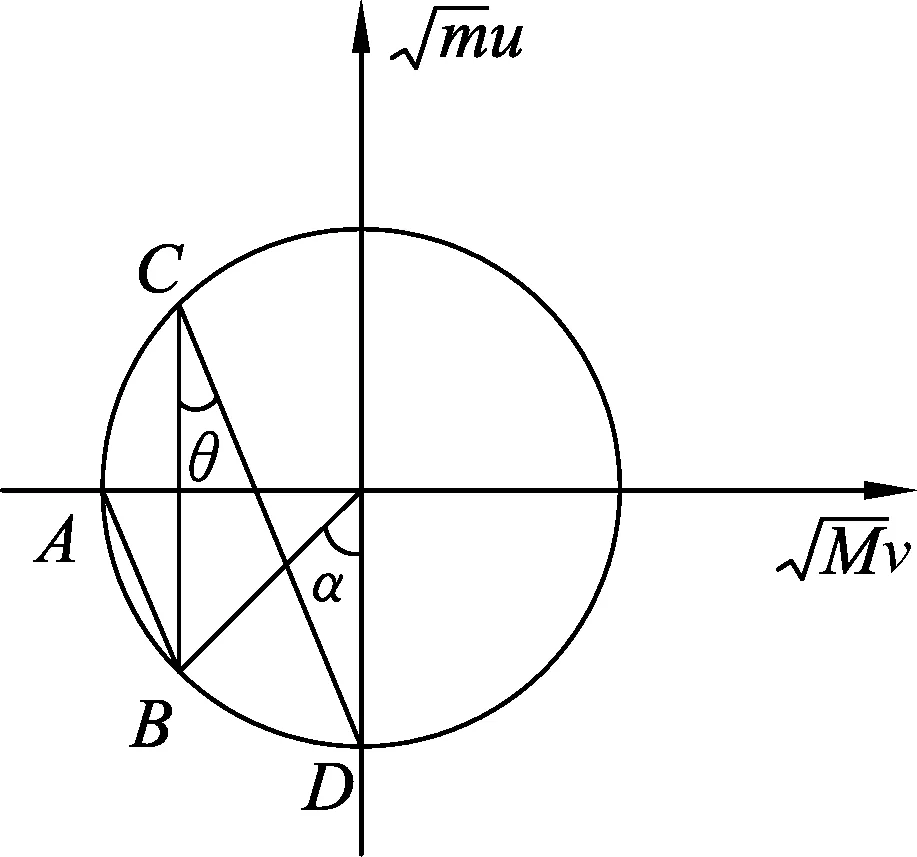
图3 速度相空间轨迹示意图

mu1+Mv1=Mv0=C.

(4)

坐标移动到B点,根据(4)式有AB斜率为

(5)

第1次碰撞后,m将向左并与墙壁发生碰撞,速度反向,而M速度不变,因此第2次碰撞后速度坐标与B点关于水平轴对称,位于圆上C点,之后发生第3次碰撞为两滑块间碰撞,同样根据动量守恒得到类似(4)的等式

mu3+Mv3=mu2+Mv2=C.

(6)

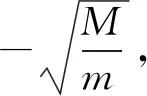
(7)

由圆的几何知识:一段圆弧对应的圆心角是圆周角的2倍,可知

(8)

(9)

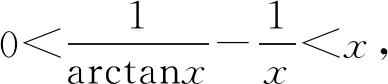
(10)

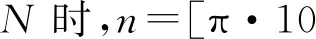
3 总结

本文通过速度相空间的方法巧妙的求解了碰撞次数,将力学过程几何化,直观清晰,这也反映了物理与数学的内在关联之美．