适用汽车散热器试验的小型风洞收缩段设计及结构改进分析*

张 威

(武汉交通职业学院，湖北 武汉 430065)

冷却系统是汽车发动机的重要组成部分，散热器又是其核心部件[1]。散热器的散热性能对冷却系统至关重要，同时也影响整车的经济性和工作效率。散热器的设计通常先用数值模拟的方法进行模型设计、仿真验算等，再通过风洞试验进行实证[2]。

散热器位于发动机前部，为发动机提供散热，保证发动机的良好运行。目前，散热器的数值模拟已经有了很多研究：韩占钟等[3]阐述了如何利用Fluent软件对散热器进行优化设计；张行周等[4]建立了基于散热器微元结构的动态传热模型，并利用MATLAB/SIMULINK对其仿真模型进行了分析；袁兆成等[5]利用CFD对结构复杂的管带式散热器进行了仿真研究。还有些学者对风洞的结构进行了研究：王帅等[6]使用CFD软件对两种风洞的收缩段壁型进行了全面的仿真分析，通过比较、探讨两种收缩曲线对收缩段内流场的影响，提出了风洞收缩段参数化设计的想法。张连河等[7]采用CFD软件对比分析不同速度条件下维辛斯基收缩段的流场品质，得出能提高收缩段加速性的结论。

前期研究大多侧重于理论部分，对风洞结构的研究也大多关注收缩段的曲线，但是对收缩段的维氏曲线和双三次曲线对风洞性能的影响缺少研究，本文将对此问题展开研究。

1 风洞试验小型化设计

国内风洞结构设计一般以国防科研试验工程技术系列教材之《高低速风洞气动与结构设计》[8]《风洞设计原理》[9]为理论指导，本设计也将参考以上两本教材并结合国内同类型风洞的设计经验对各结构、尺寸进行确定。

1.1 小型风洞试验台设计

根据散热器工作的实际情况，散热器的风洞试验台属于低速风洞(风速≤0.4马赫[10])，因大型风洞试验台占地面积大且造价高昂。为了降低试验成本同时满足试验精度，对低速风洞进行小型化研究具有非常重要的意义。

如图1所示为常见低速直流式风洞的气动结构布置图，主要由试验段、稳定段、收缩段、尾部扩散段、圆方过渡段、动力段等部分组成。

1-动力段；2-整流头罩；3-预旋片(前导叶)；4-风扇；5-止旋片(后导叶)；6-整流尾罩；7-圆方过渡段；8-蜂窝器；9-稳定段；10-收缩段；11-试件；12-试验段；13-尾部扩散段图1 直流式风洞的气动结构布置图

图1中编号11为试件，从图中可以看出试件的大小决定了风洞的大小，为了将风洞小型化，就需要进一步将试件小型化。散热器的截取部分包含若干散热带和散热扁管，如图2所示。散热带呈周期性排布，并由翅片组成，散热扁管紧贴散热带排布[11]。

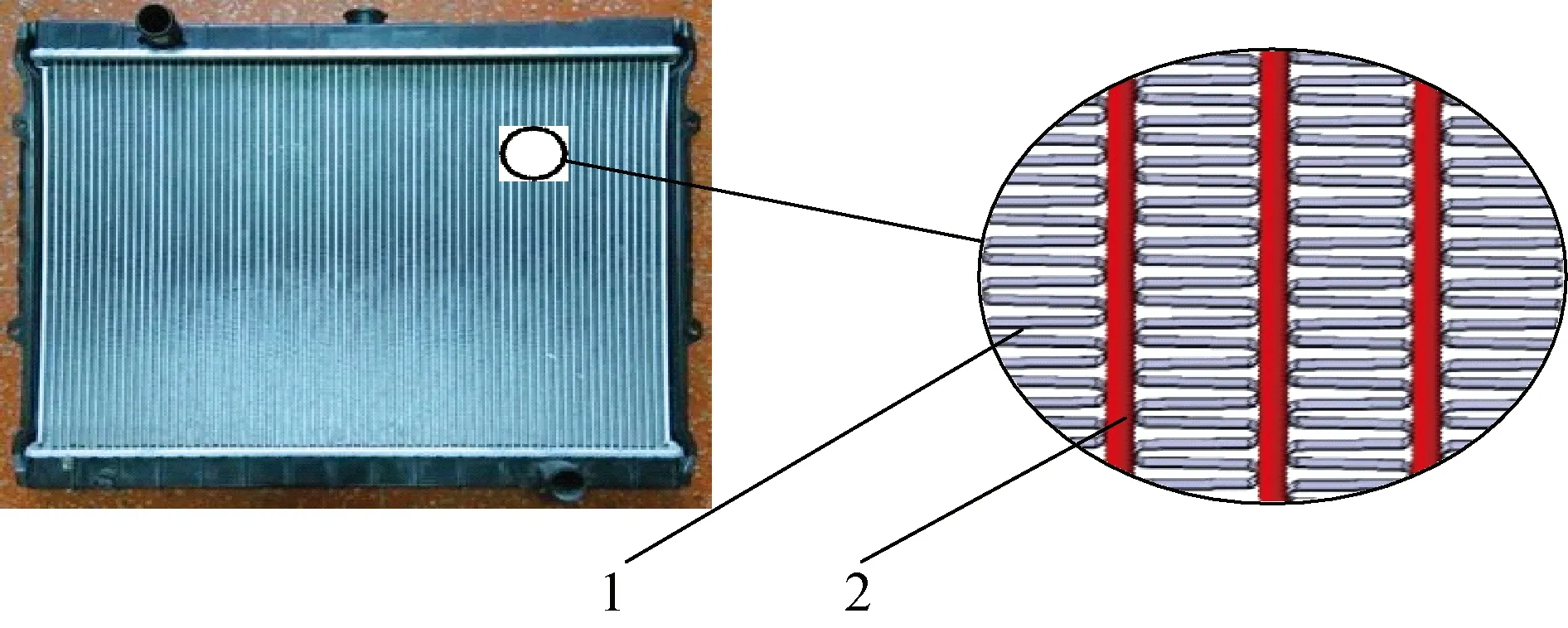
1-散热扁管； 2-散热带图2 散热器及局部放大模型

在进行风洞试验时，需要给散热器接入热水，模拟散热器正常工作时的状态，测试散热器的工作参数。热水进入散热器和排出散热器需要额外的管路，为了小型化的需要，省略散热器的热水管，给散热器贴硅胶发热片加热，模拟散热器的工作状态。同时，将测试件等比例缩小，以满足小型化的需要。例如，某车型散热器芯的尺寸为381.25 mm(宽)×590 mm(高)，对其小型化后将芯体尺寸缩小一半左右，即测试件尺寸为190 mm×280 mm。

1.2 小型风洞收缩段设计

收缩段是非常重要的一部分，它能使来自稳定段的气流均匀地加速到设计风速，并改善试验段入口的流场品质。收缩比为收缩段前、后截面积的面积比，提高这个数值有利于降低湍流度及风机效率，即提高风洞流场品质和经济性，Fang F M等[12]提出收缩比为2.8，本小型化风洞也选择此收缩比。已知进出口截面比为2.8，出口处截面即为试验段入口截面190 mm×280 mm，很容易计算出收缩段入口截面Wcon1=330 mm，Hcon2=450 mm。

收缩段曲线的形状在很大程度上影响着试验段入口气流的速度均匀性，该曲线应尽量使沿壁面的气流流速稳步递增，并保证不产生附面层剥离现象，同时也能保证该段入口与出口的气流流速平行于轴向。常见的收缩曲线有维辛斯基(Witozinsky)曲线、双三次曲线和五次方曲线。默认设计将采用国内研究最为常见的维氏曲线与双三次曲线进行对比分析。

2 收缩曲线

收缩段能均匀加速气流，并使气流进入试验段时达到设计速度。良好的收缩段设计应避免气流在洞壁出现分离，同时保证出口气流的均匀与平稳。为了设计出流场品质较好的收缩段，本文首先建立收缩曲线和公式[6]，然后采用Fluent软件对维氏曲线和双三次曲线收缩段结构进行对比分析。

2.1 维氏曲线模型

文中所采用风洞模型的收缩曲线均轴向对称，收缩曲线可用图3来表示。

维氏曲线的尺寸公式为

(1)

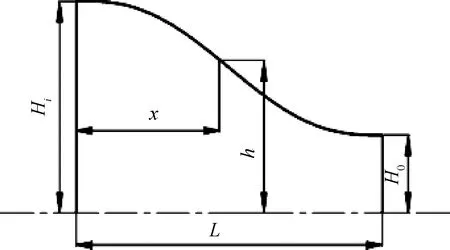
图3 收缩曲线

根据维氏曲线尺寸公式分别建立若干点组，每种曲线各有两组，分别对应高和宽所连接的收缩曲线，如表1所示。

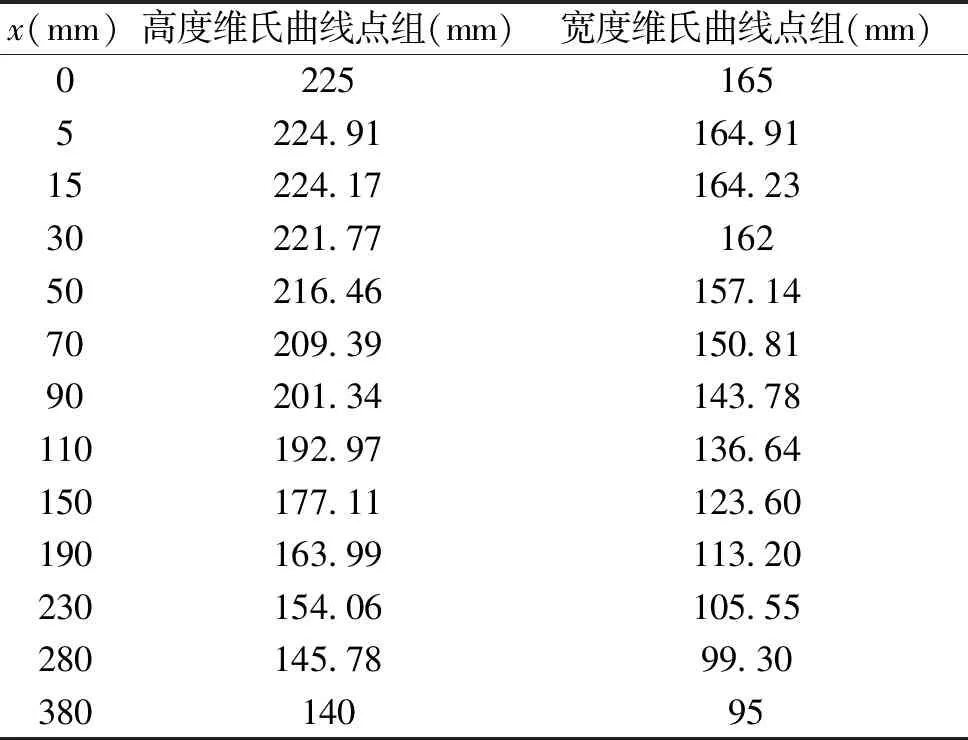
表1 维氏曲线点组

2.2 双三次曲线模型

双三次曲线的尺寸公式为

(2)

其中：xm为横坐标x与收缩段长度L的比值，取值为0.55。根据双三次曲线尺寸公式分别建立若干点组，每种曲线各有两组，分别对应高和宽所连接的收缩曲线，如表2所示。

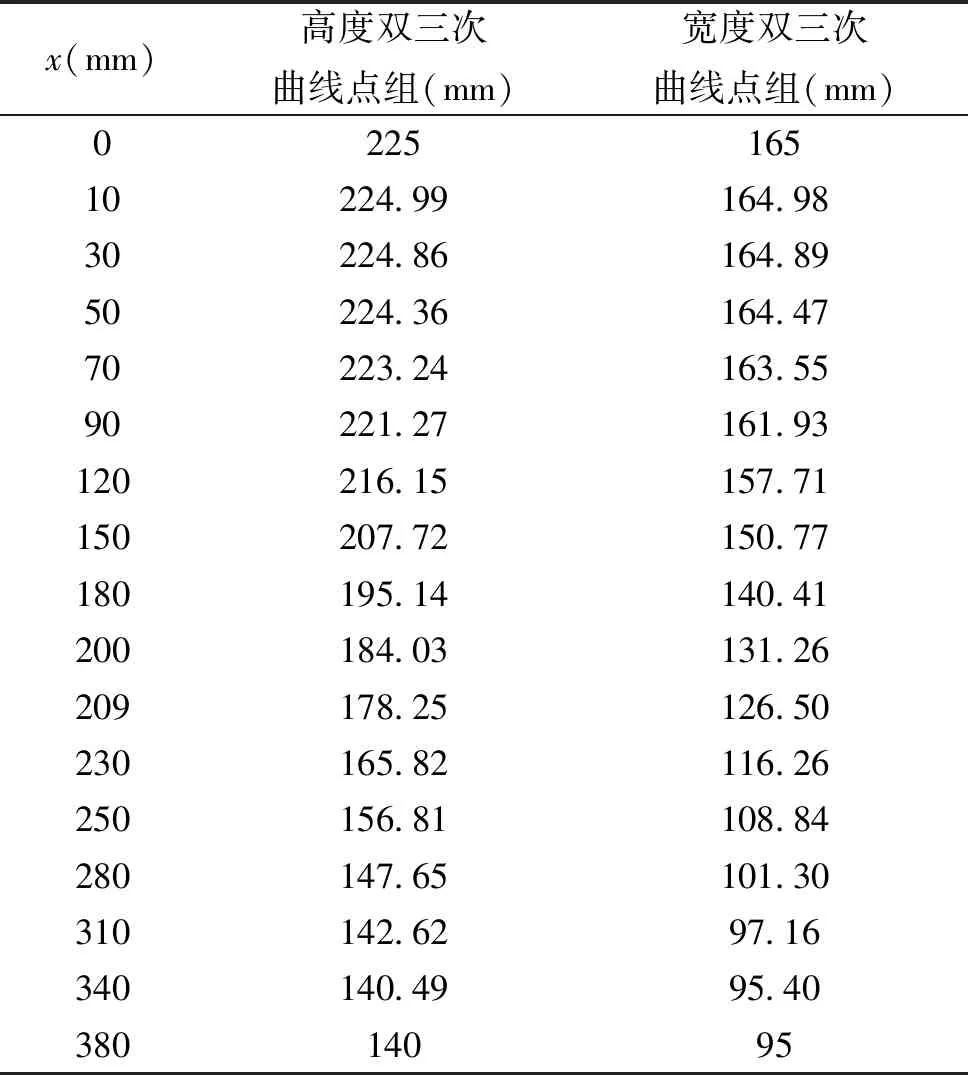
表2 双三次曲线点组

2.3 点组建模

根据以上点组在CATIA曲面设计中完成两种收缩段结构的建模，并将模型导入ICEM中进行网格划分，考虑到边界层效应，壁面附近的网格密度应大于核心区域的网格密度。如图4所示。

图4 收缩段模型网格划分图

3 计算与仿真分析

从速度迹线图5(a)和5(b)可以看出，两种收缩段出口最大速度约为8 m/s，而入口速度设置为2.87 m/s，与面积比2.8的结构属性吻合，同时能简单计算出两种结构的动压增量约为33.46 Pa。而从静压云图 5(c)和 5(d)可以看出，两种结构的前后静压差约为35 Pa，与动压增量相匹配，符合一般规律。

图5 收缩段速度迹线图与静压云图对比

观察静压云图与速度迹线图的入口处发现，维氏曲线与双三次曲线相比，静压降低更快，速度增加更快。因此，相较于双三次曲线收缩段，维氏曲线收缩段在入口处更容易出现逆压梯度及壁面气流速度分离的现象。同时可以明显地看出，双三次曲线收缩段入口处静压分布均匀，最大相对静压37.22 Pa；而维氏曲线收缩段入口处静压分布不太均匀，最大相对静压为出现在边角处的37.87 Pa，使得速度容易向核心区集中，造成流场速度不均，并增大壁面气流分离的可能性。通过对两种曲线收缩段结构入口处的分析可知，维氏曲线入口处气流更容易出现壁面分离，速度向核心区集中，影响入口流场均匀性；而双三次曲线入口处气流则显得更加稳定、均匀。

观察静压云图与速度迹线图的出口处发现，双三次曲线降压与增速相对较快，出口处压力分布较为均匀，速度迹线平稳；而维氏曲线则在边角处出现相对的负压，这容易造成角落处的速度集中，影响试验段入口处的流场均匀性。根据以上分析，维氏曲线在入口处收缩较快，增速与降压过冲，因此更容易产生气流分离现象；同时维氏曲线的最大与最小相对静压分别出现在入口与出口的边角处，造成了速度集中，这对改善流场的速度均匀性是不利的。

通过两类云图对两种收缩段结构进行了定性分析，为了更加准确地分析流场，下面将对沿轴向分布的压力及速度数据进行提取分析，得出相对静压分布图和轴向速度分布图，如图6和图7所示。

图6 相对静压分布图

图7 轴向速度分布图

由图6可知，两曲线入口静压分别为34.6 Pa和34.44 Pa，出口处则均为0 Pa。两条曲线随轴向距离增加非单调递减。两曲线进口处的压力变化均较为平缓，维氏曲线相较于双三次曲线静压总体偏小，从距离入口20 mm处开始，维氏曲线静压值迅速降低；而双三次曲线则平稳下降，至距离入口180 mm处，维氏曲线相对静压19.92 Pa，双三次曲线相对静压28.94 Pa，两者静压值相差 9.02 Pa。气流在经过收缩段中部之后，两曲线的降压趋势才基本一致。

由图7可知，两曲线入口速度均为2.87 m/s，出口速度均为8.02 m/s。两条曲线随轴向距离增加均非单调递增。从收缩段入口处来看，双三次曲线速度增长缓慢，直到60 mm处仍保持平稳，增速不到0.04 m/s；维氏曲线在入口处则增长更快，在180 mm处达到了5.65 m/s，而双三次曲线则仅为4.14 m/s，相差1.51 m/s；在气流达到收缩段尾部时，两者的速度才趋于一致，达到8 m/s。

综上，双三次曲线的特点是在入口处静压的降低及速度的增长都非常缓慢，在中后部的时候静压与速度都分别有显著的降低和增长，气流达到尾部时两种变化都趋于平缓；维氏曲线的特点则是降压与增速在入口处变化剧烈，而在出口处则较为平缓。因此，维氏曲线收缩段在入口处容易产生洞壁的气流分离并出现逆压梯度，而双三次曲线则较好地克服了以上弊端。所以，收缩段选择双三次曲线构型并用于后文整体风洞模型的搭建。

4 散热器风洞试验验证

如图8所示，本散热器风洞试验台属于某车用发动机有限公司，该试验台可对散热器进行散热性能试验、水力阻力试验(简称水阻试验)、空气阻力试验(简称风阻试验)。本文仅对风阻试验进行介绍，测量值为试件入口风速及试件前后压力降。

1-散热试件进口；2-散热试件；3-散热试件出口；4-风机；5-供水管路；6-回水管路图8 散热器风洞试验台

4.1 相关技术指标

芯体试件尺寸规格：300 mm×300 mm～1000 mm×1000 mm；试件入口流速：0.3～15 m/s;风扇转速：300～4000 r/min(精度≤±5 r/min)；散热器进、出风压力：-10～10 kPa(精度: ±0.3%)；系统测试误差≤±3.0% FS。

4.2 试验设备

试验设备包括风洞水循环系统、水循环加热设备、水泵、风机、测试仪器及控制系统等。因为测量项目仅为风阻试验，因此只介绍与此相关的风机、测试仪器及测控系统。

(1)风机：采用45 kW，高转速0～3000 r/min的变频电机，变频器选用富士FRNP11/G11，能在各种运行条件下实现对电动机的最佳控制，并能无冲击瞬停再起动运行。

(2)测试仪器：因要求试件入口风速达到8 m/s，故选用毕托管配合压差变送器对入口风速进行测量，在试件前后距离为D(散热芯体水力直径)的位置各布置一个总压探针并配合压差变送器对压降进行测量。

(3)控制系统：包括微机系统、PLC系统等。控制系统采用Mod Bus总线，并用工控机作为主机对系统进行控制。微机系统由工控机与打印机组成，它与下位机PLC通过Mod Bus总线相连，并将测量仪器上传的数据信号存储于数据库中，形成测试报告。下位机采用PLC系统，便于对风机、加热设备、水循环等系统的控制并进行数据采集。

4.3 试验条件

目标试件为型号J42-1301110的管带式芯体，管子数49根，散热带数50条，散热带波距2.5 mm，散热带波高7.5 mm；室温31.3 ℃，湿度8%，气压98.9 kPa。从风洞进风口处3D(D为动力段内径)距离内不得有遮挡物，进风口边下部距地面距离应大于D。

4.4 试验方案及测量结果

先对速度场系数进行测量(表征均匀性与稳定性)，在速度场系数符合要求后便对截面中心的风速进行测量。保证入口风速为2 m/s、4 m/s、6 m/s、8 m/s时，每种流量工况测量四次，四组测量结果如表3所示。

表3 风阻试验结果

4.5 对比验证

对应试件入口的四种风速，根据截面比将整体风洞数值模型的入口速度分别设定为1.5 m/s、3 m/s、4.5 m/s和6 m/s。分别计算出试件前后截面(N-O)的总压值，并换算成对应的总压差。将试验与仿真所得的压差值进行比较，如表4和图9所示。

表4 试验与仿真的压差值比较

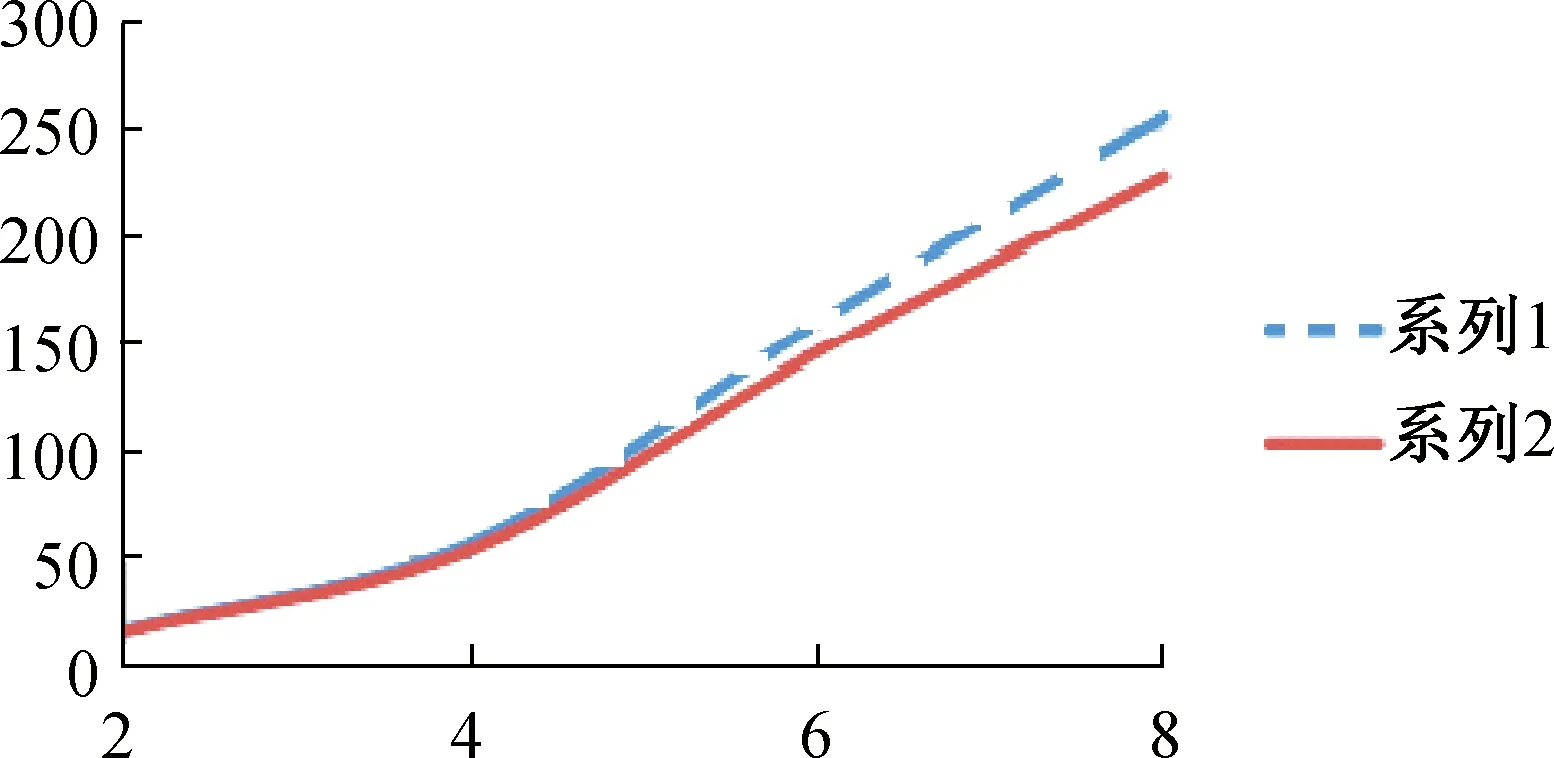
1—压差试验值； 2—压差仿真值图9 试验压差与仿真压差比较

表4和图9分别将试件前后压差的试验值与仿真值进行了比较，可以看出其变化规律基本一致，压差值都是随着速度的增加而非线性递增，变化规律与速度比的平方相关。通过对比发现，试验值与仿真值的最大偏差出现在最大速度入口，偏差值为10.92%；最小偏差出现在最小速度入口，偏差值为4%，因此验证了本文设计的气动结构较为合理。

5 小结

本文首先根据实际需求，提出风洞小型化设计，并根据教材与同类型风洞设计经验建立了小型化风洞试验台，对风洞收缩段进行设计，采用Fluent软件对维氏曲线和双三次曲线收缩段结构进行对比分析。

然后通过计算与仿真，对压力云图及速度迹线图的定性分析以及对沿轴向速度分布与压力分布曲线的定量分析，发现维氏曲线收缩段在入口处容易产生洞壁的气流分离并出现逆压梯度，而双三次曲线则较好地克服了以上弊端，显得更加稳定，进而确定收缩段选择双三次曲线构型。

最后进行散热器风洞试验验证，通过将真实风阻试验测量值与模拟仿真试验计算值对比验证，发现最大误差为10.92%，验证了所设计气动结构的合理性。为适用汽车散热器试验的小型风洞收缩段的设计提供了切实可行的方案，具有一定的指导意义和参考价值。