基于概率线路图的仓库移动机器人避障路径跟踪研究*
2021-03-29罗国荣
罗国荣
(广州科技职业技术大学,广东 广州 510550)
随着电子商务的发展和成熟,以及新冠病毒疫情的影响,对仓储物流的需求非常大,传统仓储物流的效率也跟不上现代物流的快速发展,因此,发展基于智能移动机器人的智能仓储物流技术是解决快速物流的重要技术之一。移动机器人要在仓库中实现自动拣卸货,需要求解移动机器人路径规划的问题,以实现高效、无碰撞地在仓库中移动。唐淑华等利用JAVA语言提取仓库地图的信息,并结合最邻近算法和迪杰斯特拉算法进行避障的计算,实现最短路径规划。但其存在计算量和存储空间占用大以及容易陷入局部最优的缺点[1]。夏铜辛等提出一款智能的仓库巡逻机器人,能通过OpenMV摄像头对仓库进行实时巡逻,但机器人移动路线是事先定义的,当仓库地图更新后,需要重新自定义移动路径,才能实现智能的路径规划跟踪[2]。林显其提出一种基于图像识别AGV仓库搬运机器人,通过视觉处理和Dijkstra算法实现运动轨迹的规划和自动避障,但其Dijkstra算法不能有负权边的局限制约着仓库路径的规划[3]。孙海提出一种动态加权A*算法,并结合二次路径规划方法,有效减小规划后的路径距离[4]。丁艳等提出基于蚁群算法的多移动机器人避障路径规划方法[5]。陈玉龙等提出一种基于障碍物STL模型的移动机器人避障方法[6],实现机器人避障路径规划,提高了移动机器人路径规划的整体性能,但没能与路径轨迹跟踪有机地结合起来控制移动机器人的避障运动。韩军政等提出一种BP神经网络PID控制方法,利用BP神经网络学习算法实现了PID三个参数的在线自整定[7],能满足机器人避障运动的控制要求,但没有给出有效的路径规划。为实现移动机器人在仓库中实时快速自动拣卸货,本文提出了一种基于概率线路图(PRM)优化的纯追踪路径跟踪算法,该算法能解决移动机器人在不稳定仓库环境中的实时无碰撞运动规划跟踪问题。通过matlab仿真软件设计仓库场景并对算法进行仿真,仿真结果证明了该方法的有效性和安全性。
1 PRM算法思想
概率线路图(PRM)算法是基于离散采样的路径规划算法,其思想是先把移动机器人所处的工作环境转换为一幅二值灰度网格图,并在这一幅网格图中进行随机采样,把采样点组织起来构成一个节点集合Q,再进行碰撞检测以去除位于障碍物内的点,得到一个无碰撞的节点集V,然后将节点集V中的各点进行连线得到连线集合E,利用这个节点集V与连线集合E构建一个无向网络图G(V,E),再通过A*算法搜索一条可行的路径。该PRM算法分预处理和路径搜索两个阶段。
预处理阶段的步骤如下:
(1) 将工作环境地图转换为二值灰度网络图,随机采样n个采样节点并构成点集合Q。
(2) 把无向网络图G(V,E)初始化为空,在点集合Q中均匀随机抽取一节点nj,并判断节点nj是否位于障碍物内,若位于障碍物内则丢弃该点,否则将该点加入到无碰撞点集合V中。
(3) 建立启发评估函数以判断无碰撞点集合V中任一节点ni与节点nj的距离是否小于阀值距离p,若小于阀值距离则称节点ni为节点nj的邻域点,并将这两个节点连接生成连接线li,j。启发评估函数采用殴几里德距离计算公式
(1)
式(1)中,d为一对节点(ni,nj)殴几里德距离,N为无碰撞点集合V的最大个数。
(4) 检测连接线li,j是否与障碍物发生碰撞,如果无碰撞,则将其加入到连线集E中。
(5) 重新执行上述(2)至(4)的操作,直到点集合Q中的采样点抽取完毕。最后输出一个无向网络图G(V,E)。
路径搜索阶段是采用A*算法进行求解最优路径,A*算法是一种求解最短路径最有效的启发式算法,其原理是在节点集合V中利用代价估计函数对每一个节点的位置进行评估,获得最好的节点位置,再从这个节点位置进行搜索直到到达目标。代价估计函数为
F(n)=G(n)+H(n)
(2)
式(2)中,F(n)为代价估计函数,表示从初始节点通过节点n到达目标节点的最小代价路径的估计值;G(n)表示从初始节点到n节点的已完成的实际代价;H(n)表示从n节点到目标节点的最优路径的预计代价,其公式为
(3)
式(3)中,cx为当前节点的x轴数值,gx为目标节点的x轴数值,cy为当前节点的y轴数值,gy为目标节点的y轴数值,D(i,j)表示节点i与节点j之间的殴几里何距离,其公式为
(4)
式(4)中,xi为节点i的x轴数值,xj为节点j的x轴数值,yi为节点i的y轴数值,yj为节点j的y轴数值。
A*算法的步骤如下。
(1) 设置超始节点s和目标节点g。为了表示所有已生成而未考察的节点,将上述求得的无碰撞点集合V转换为open列表;为了表示获得最佳路径点,创建close列表。初始化close列表为空。即是open={V},close={ }。
(2) 判断open是否为空,若为空,即表示没有路径节点,也就没有最优路径,因此,这种情况下退出计算,结束搜索。
(3) 在open列表中利用公式(2)取出F(n)值最小的节点n,并把节点n加入到close列表。
(4) 判断节点n是否为目标节点g,若是则表示成功搜索到目标节点,结束搜索,并把close列表中的所有节点连接起来即为寻找的最优路径。
(5) 若节点n不是目标节点,扩展节点n的所有后继子节点,并把这些后继子节点组合起来构成节点集合M。
(6) 对节点集合M的节点元素p,并计算F(pold)值,然后分别作两类进行处理:
①若节点元素p都不属于open列表和close列表,将其加入open列表,并为节点元素p分配一个pold→n的指针。
②若节点元素p属于open列表,计算F(pnew)值,并与F(pold)值比较,若小于F(pold)值,表明找到了一条更好的路径,并更改指针,即pnew→n;若等于或大于F(pold)值,表明没有找到一条更好的路径,则保留原来的指针,即pold→n。
(7)转到步骤(2)继续运行。
整个步骤流程如图1所示。
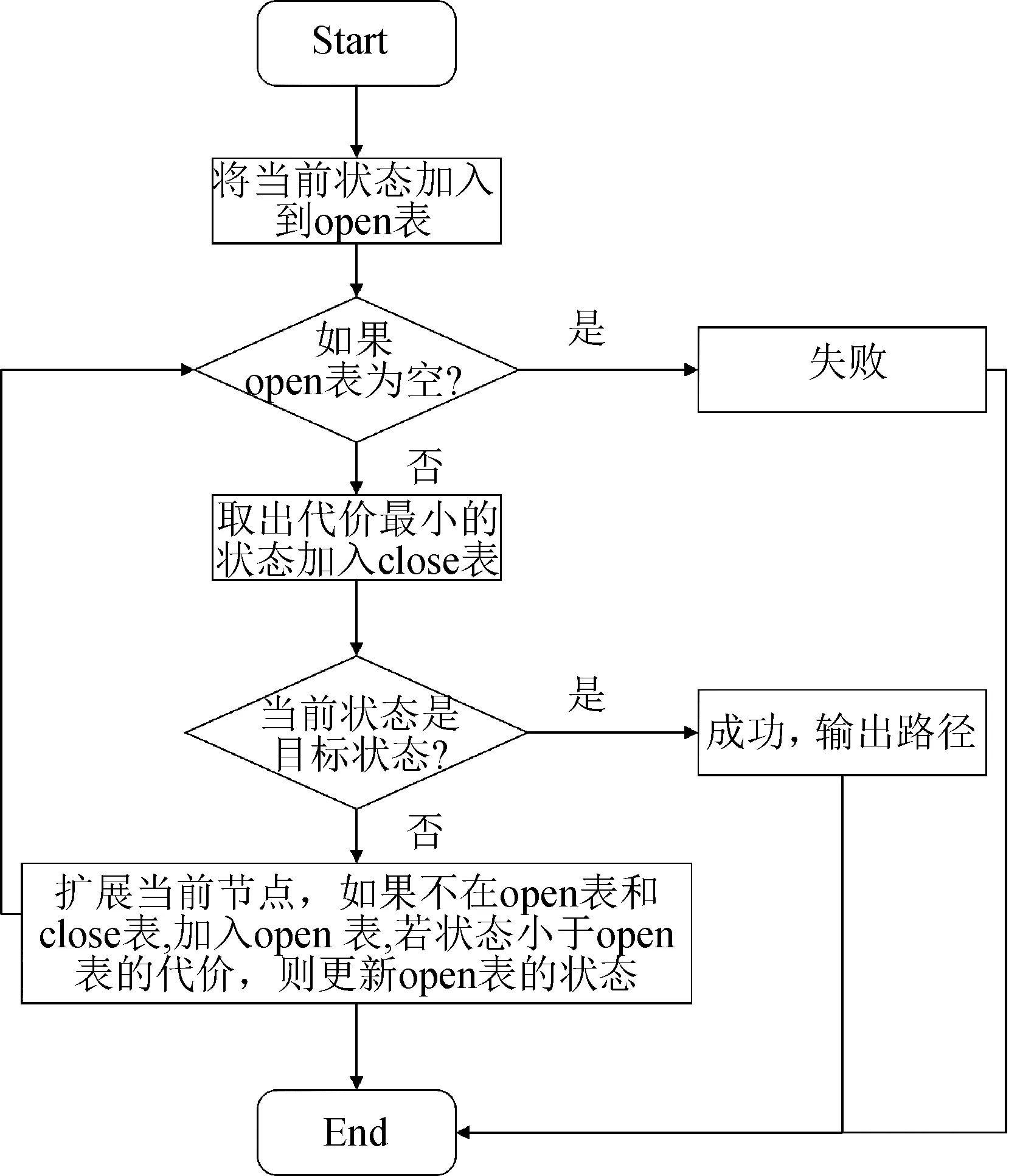
图1 A*算法流程图
2 PRM算法优化
由于PRM算法在地图中采样是随机抽取的,可能导致采样点分布不均,增加求解最优路径失败的概率,所以需要适当增加该算法的采样点数目,尽量使随机采样的点能均匀地分布在地图中的每个角落,从而增加搜索最优路径成功的概率。但过多地增加采样点数目会增加计算量,导致PRM算法整体求解最优路径的效率下降,因此,可通过改变连接点的连接阀值距离来提高运算效率。
连接阀值距离是地图中连接点的距离上限。在此距离内,每个节点连接其周围的所有节点,它们之间没有障碍。通过降低连接距离,可以限制连接数量,以减少计算时间和简化地图。但是,较低的距离限制了寻找完整无障碍路径的可用路径的数量。所以,需要根据地图的复杂程度来调节阀值连接距离,当地图简单时,可用少量节点和更大连接阀值距离来提高效率。当存在大量障碍物的复杂地图时,可用较多的节点和更大连接阀值距离来提高算法效率。
3 纯追踪算法轨迹跟踪模型
纯追踪算法是基于几何追踪的方法,该算法是在平面、无侧滑、低速度行驶的前提下将四轮移动机器人简化为两轮自行车模型,特别适合仓库的应用环境,如图2所示。
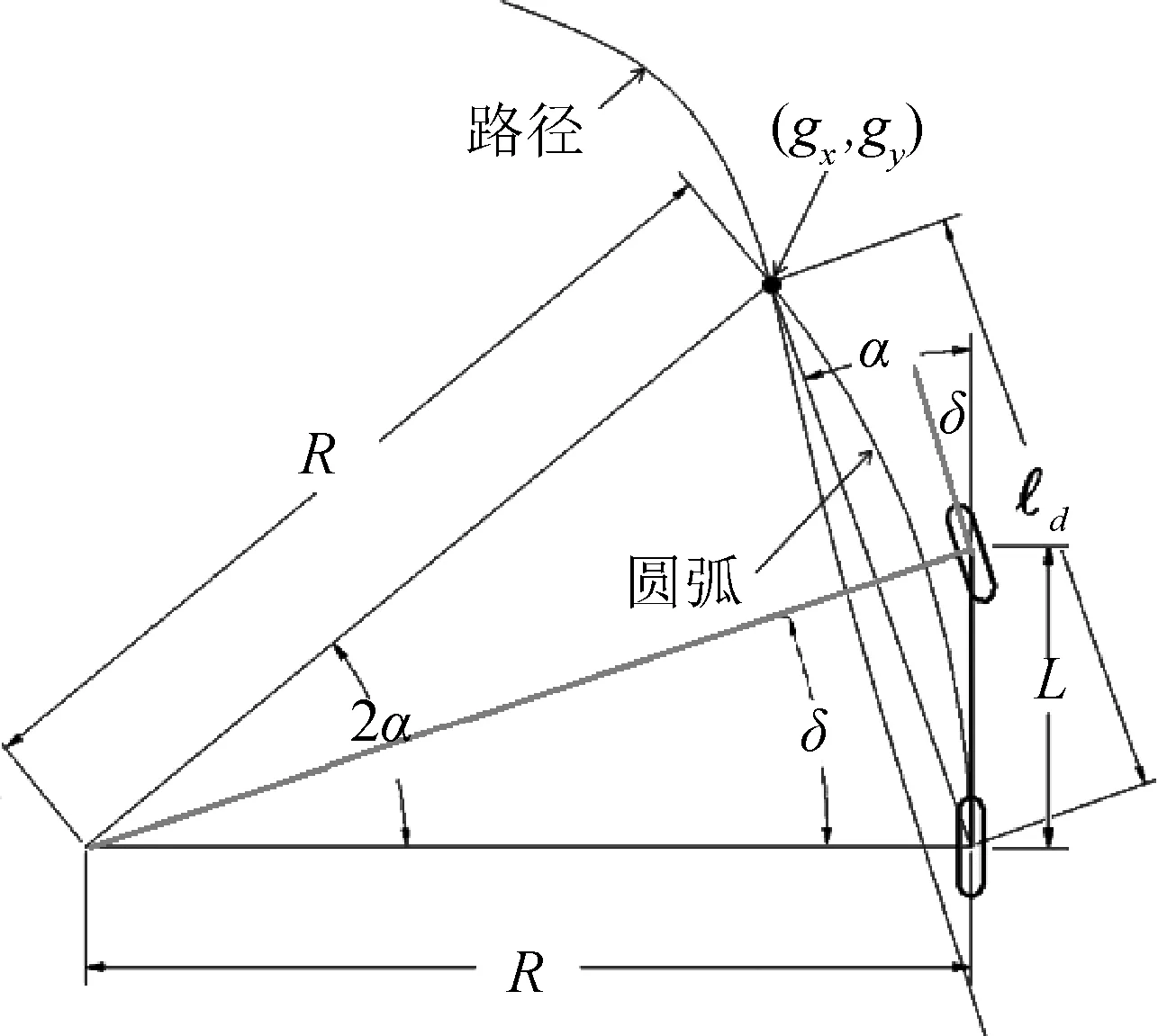
图2 两轮自行车模型
纯跟踪算法以汽车的纵向车身为切线,后轮为切点,通过调整前轮转向角,使汽车可以沿着一条包含目标路点(gx,gy)的圆弧行驶。设δ为车身和目标路点(gx,gy)的夹角,L为移动机器人轴距,R为在给定的转向角下后轴遵循着的圆的半径,由三角函数和正弦定理可知
(5)
(6)
由于道路的曲率为
(7)
可将式(6)化简为
(8)
根据式(5)、式(7)和式(8)可得:
(9)
将时间变量t引入,则前轮转角控制公式为
(10)
d=Κvy
(11)
式(11)中,Κ为调节系数,vy移动机器人纵向速度,将式(11)代入式(10)可得:
(12)
4 算法仿真及结果分析
本文的仓库模拟场景如图3所示,移动机器人的任务是从充电站出发,达到分拣站装载包装好包裹,通过概率线路图路径规划算法规划出一条可行的避障路径,并应用纯追踪路径跟踪算法控制移动机器人移动,将包裹运送到货架储存,之后返回充电站。
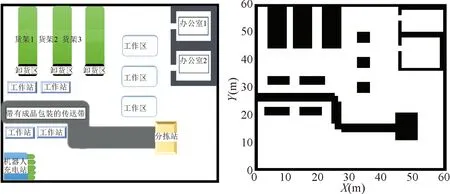
图3 仓库场景及二值网格图
试验是在Matlab2020a软件环境下完成的。硬件环境中的CPU采用主频为2.4 GHz的英特尔酷睿四核i7-10750H处理器,显卡采用显存为4 GB的GTX1650Ti显卡,内存16 GB。构建的试验仿真模型如图4所示。试验仿真模型是由移动机器人调度器、PRM算法规划器、纯追踪轨迹跟踪器、移动机器人运动学模型和结果可视化模型组成。
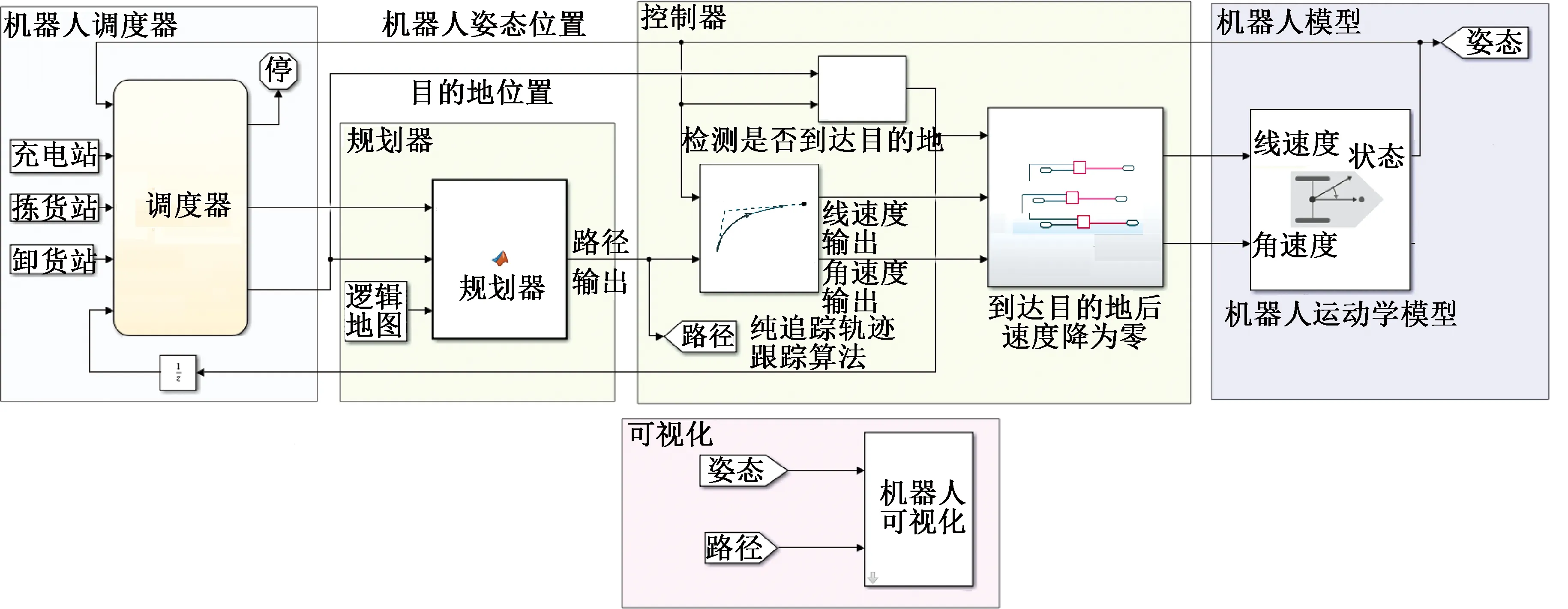
图4 试验仿真模型
为了验证采样点数目的适当增加能加大搜索最优路径成功的概率,在设定连接阀值距离为10 m的情况下,采样点数量分别设置15、50、150,进行了100次重复性试验,对比这3种情况下算法的仿真结果,如表1所示。

表1 增加采样点数量的100次重复性试验结果
从表中的数据可以看出,随着采样点数据的增加,其路径规划的成功率也增加。当采样点数量为15个时,规划路径的成功率只有35%,如图5所示,由于随机分布的采样点数量少,而且分布不均,仓库阻碍物的阻挡,导致路径规划容易失败。
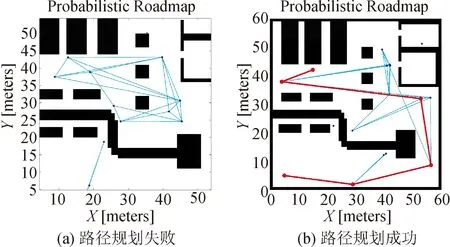
图5 采样点数量为15个时的路径规划效果
当采样点数量为50个时,规划路径的成功率提升到93%,如图6所示,由于采样点数量的增加,其采样点分布较均匀,导致路径规划的成功率大为提升。当采样点数量为100个时,规划路径的成功率提升到100%,但其消耗的计算时间也相应地增加,如果无限地增加采样点数量,会使算法的实时性下降,因此,需要根据项目的实时性要求适当地增加采样点,从而达到提高规划路径成功率的作用。

图6 采样点数量为50个时的路径规划效果
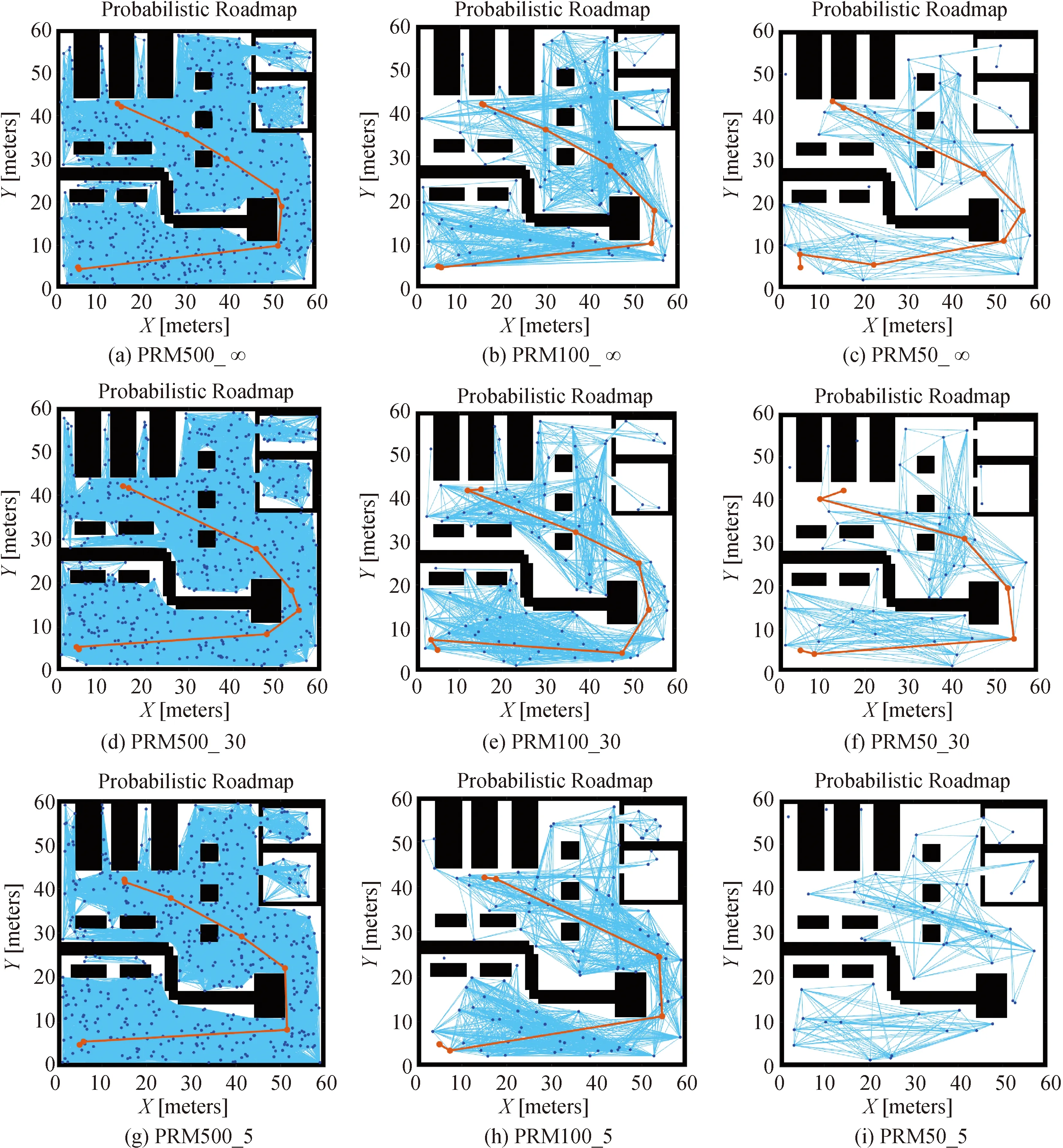
图7 9种情况下算法的仿真结果
为了验证采样点数量与连接阀值距离之间的匹配关系,采样点数量分别设置500、100、50,连接阀值距离分别设置为5 m、30 m、∞m,上述设置组合出9种情况,对比这9种情况下算法的仿真结果如图7所示。
图7(a)(b)(c)中显示当连接阀值距离为∞m时,3种采样点数量的仿真结果。当采样点数量为500个时,随机采样点相对较多,能均匀地分布在地图中,规划出的连接线数量也较多,其计算机运算耗时最长。当显示采样点数量为100个时,随机采样点明显减少,其采样点已不能有效地均匀分布在地图中,规划出的连接线数量是也明显减少的,其计算机运算耗时较短。
当显示采样点数量为50个时,随机采样点不能均匀地分布在地图中,规划出的连接线数量最少,但其计算机运算耗时最短。如图7(i)所示,当采样点数量为50个、连接阀值距离为5 m时,虽然计算机运算耗时较短,但A*算法无解,找不到可行的最优路径。
上述9种情况下的计算机耗时如表2所示。可以看出随着采样点增多,成功规划出路线的概率越大,相应的计算机耗时也增加,因此,可通过减少采样点数目来优化PRM算法,但过量地减少采样点数目,会使算法不完备,求解不出最优路径。本试验中,当采样点数目为50个时,进行了100次重复性试验,失败次数达20次,成功率为80%,而当采样点为100个和500个时,同样进行了100次重复性试验,成功率为100%。当采样点数目固定时,适当增大连接阀值距离可有效减少计算耗时,提高运算效率。上述充分证明了通过调整采样点数目和连接阀值距离能优化PRM算法,提高路径搜索效率。
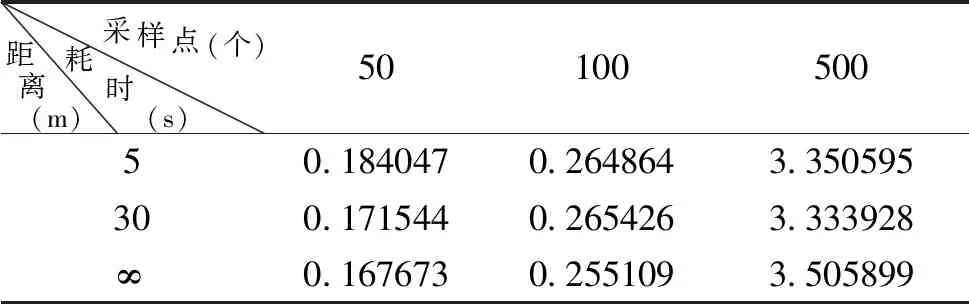
表2 9种情况下算法的运算耗时
在电脑配置、仓库地图、连接阀值距离相同的情况下,采用快速扩展随机树(RRT)算法规划的路径如图8(a)所示,其规划路径运算耗时为1.056279 s,虽然其能有效规划出路径,但并不是最优最短的路径。采用PRM优化算法规划的路径如图8(b)所示,其规划路径运算耗时为0.516794 s,时间比前者快一倍,其规划出的路径也明显优于前者,可以看出,PRM优化算法的规划效率和效果得到进一步提高。
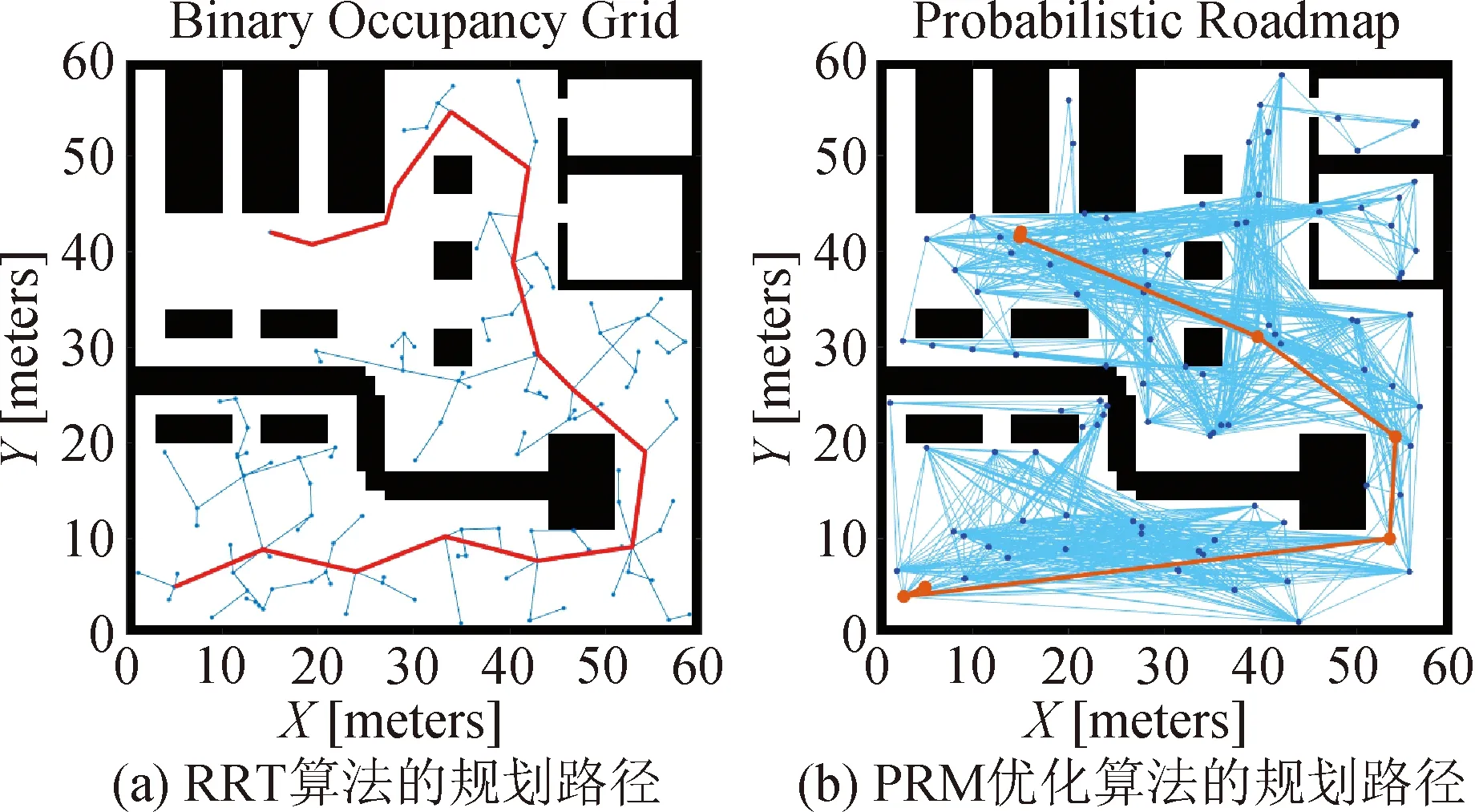
图8 RRT算法与PRM优化算法的对比仿真结果
从上述PRM优化算法求解出来的最优路径可以看出,路径虽然没有经过障碍物,但非常接近分拣站,由于算法没考虑到移动机器人的尺寸,可能会引发障碍物与移动机器人发生碰撞,为此需要将仓库地图进行尺寸扩展,如图9所示,图9(b)为障碍物尺寸扩展后的PRM优化算法规划出的最优路径,扩展的尺寸是根据移动机器人轴距的0.5倍进行,这样即可避免发生碰撞。
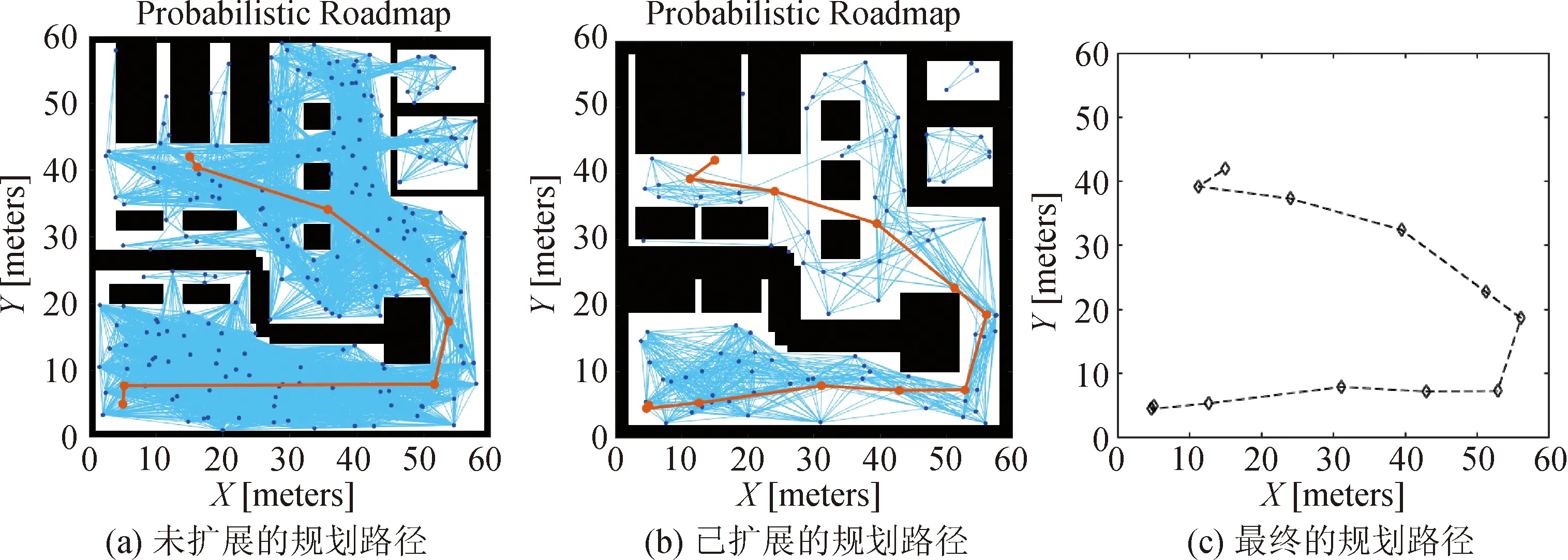
图9 地图扩展后的规划路径
把已扩展的最终规划路径与仓库原始二值地图组合起来,即可求解出无碰撞的最优路径,并将该路径输入到纯追踪算法轨迹跟踪模型,设置该模型的跟踪速度为0.6 m/s,最大角速度为2 r/s,前向距离为0.6 m,运行的结果如图10所示。可以看出,移动机器人能按照纯追踪算法的规则沿着给定的路径行驶,期间也没有与仓库中的任何障碍物发生碰撞。从仿真结果可以看出,上述设计的概率线路图(PRM)算法和纯追踪路径轨迹跟踪算法能有效地使移动机器人在仓库中进行避障行驶,表明所设计的算法具有安全性、有效性和可靠性。
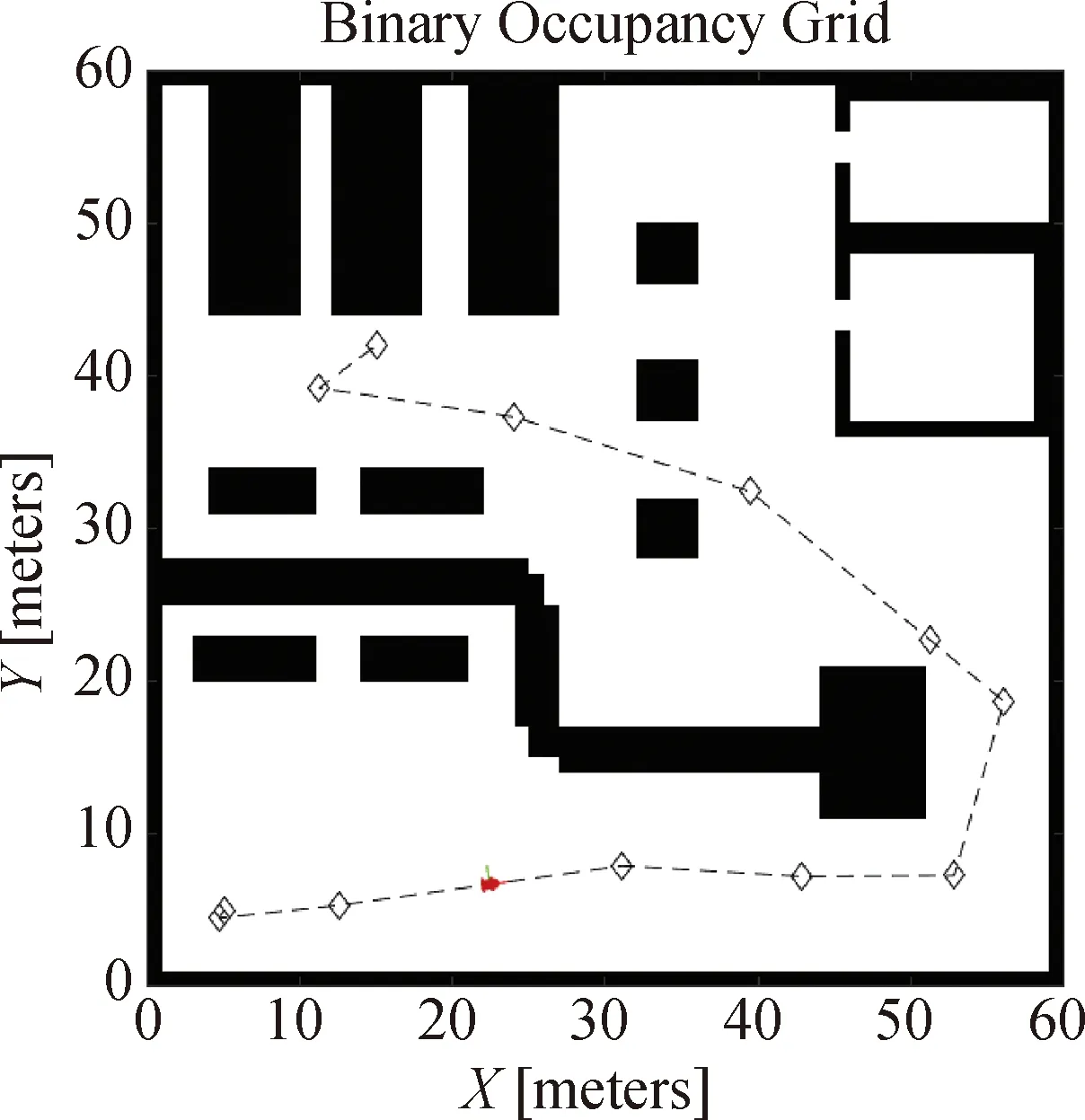
图10 移动机器人在仓库的行驶仿真结果
5 结语
本文分析研究了概率线路图(PRM)的原理和过程,针对PRM算法规划时间过慢和路径安全性不高的问题,对PRM算法进行优化。提出通过调节采样点数量及连接阀值距离、扩展仓库地图障碍物尺寸的改进方法,提高了路径规划的效率和安全性。为使移动机器人能在仓库环境下有效地跟踪路径轨迹,分析研究了基于几何追踪的纯追踪轨迹算法的原理和过程,并利用matlab软件进行仿真分析,结果表明,该PRM优化算法能使仓库路径规划效率和效果得到进一步的提升,纯追踪轨迹算法能够稳定地跟踪规划出来的参考路径,两种算法的融合能有效地提高移动机器人在仓库行驶的实时性和安全性。
