三元乙丙橡胶热氧老化试验与密封条寿命预测*
2021-03-29王安迎王林林
王安迎,王林林,王 伟
(青岛科技大学 橡塑材料与工程教育部重点实验室,山东 青岛 266042)
塑钢窗橡胶密封条是塑钢窗的重要部件,主要起密封和隔音作用。在贮存和使用中,受热、氧等外界环境不利因素的影响,其使用性能会降低,甚至因失效而报废。橡胶制品老化寿命的预测是橡胶制品使用的重要问题和研究热点。经过几十年深入的研究,各种橡胶的老化机理已经日趋完善,橡胶老化寿命的预测方法也多种多样,主要有电气工程领域采用的Dakin公式寿命推算法[1]、时温等效推算法(变量折合法)[2]和动力学曲线模型法[3]。为了保障橡胶制品能有效发挥其使用性能,提高其可靠性,需要对橡胶的贮存和使用寿命进行合理的评估。
本文主要对塑钢窗密封条所用的三元乙丙橡胶(EPDM)进行老化试验和寿命预测,验证老化寿命预测的可行性。
1 橡胶加速老化试验
橡胶材料的老化试验通常包括自然老化和人工加速老化等研究方法。科研人员最先利用自然老化方法[4]来评价橡胶材料的使用和贮存寿命,该方法是评定材料失效性的最好方法,但是由于环境测试条件难以控制、试验周期长,且材料应用的地域环境各不相同,难以在各种环境下进行不同的老化试验,所以该方法的应用比较困难。加速老化试验是根据时温等效原理来进行试验的一种方法,早期的加速老化试验主要是通过计算橡胶吸氧量来表征其老化程度。随着人们对橡胶老化机理的不断探索和深入研究,认识到了橡胶材料物理性能的变化规律,19世纪20年代研究人员运用烘箱加速老化试验的方法[5],随后出现空气弹加速老化、氧弹加速老化和人工气候加速老化的试验方法。目前,橡胶制品老化寿命的预测,通常采用与橡胶制品配方相同的橡胶试样,进行高温加速老化试验,然后通过研究橡胶试样在不同老化温度下的拉断伸长率、拉断强度、压缩永久变形等物理机械性能参数与老化时间、老化温度的变化规律,来建立老化预测模型,推算出材料在正常使用温度、某个老化程度下的使用时间,以此来表征橡胶制品的老化寿命。本研究选用拉断伸长率变化特性对橡胶的老化寿命进行预测。
1.1 试验条件
按照GB/T 3512—2001[6]1-2,将EPDM硫化胶呈自由状态悬挂于老化试验箱内,采用393 K(120 ℃)、403 K(130 ℃)、413 K (140 ℃)和423 K(150 ℃)四个老化温度,393 K和403 K的老化时间间隔为1 d、2 d、3 d、6 d、9 d、13 d、20 d和30 d,413 K和423 K的老化时间间隔为1 d、2 d、4 d、6 d、8 d、12 d、20 d和27 d,每个老化时间点取5个试样,按照GB/T 528—2009[7]进行拉伸测试。
1.2 拉伸测试
老化前橡胶试样的初始拉断伸长率测10次取平均值,老化后每个测试点的拉断伸长率测量5次取平均值。
每个橡胶试样取出后,需要在标准实验室环境中停放1 d,消除温差变化给橡胶带来的残余应力,然后再进行拉伸试验。
2 橡胶密封条老化寿命预测模型的建立
2.1 老化程度与老化时间的关系
橡胶密封条的老化性能降低率又被称为老化程度(y),在本研究中采用老化前后橡胶的拉断伸长率的比值表示。热空气老化试验获得的不同温度下老化程度随老化时间的变化曲线如图1所示。
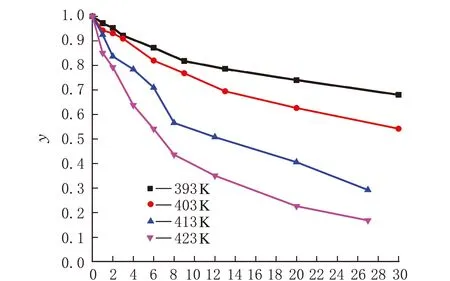
老化时间/d图1 不同温度下老化程度随老化时间的变化曲线
2.2 老化预测模型
本文采用如式(1)所示的经验公式[8]:
y=Be-kτα
(1)
式中:y为橡胶标准试样的老化程度;k为速率常数,d-1;τ为老化时间,d;B为试验常数;α为经验常数。
速率常数k与老化温度T之间的关系服从Arrhenius公式,如式(2)所示:
(2)
式中:A为频率因子,d-1;E为表观活化能,J/mol;R为气体常数,J/(K·mol);T为老化温度,K。
2.3 动力学公式经验常数α的估计
经验常数α值为0~1之间的数,为了找到合理且精确的数值,本文采用逐次逼近法来求解,利用准则I求解α值,如式(3)所示:
(3)

对式(1)进行对数变换,将动力学方程经验公式变换成式(4)所示的线性变化形式:
Y=a+bX
(4)
式中:Y=lgy,a=lgB,b=-k/2.303,X=τα。
运用最小二乘法[9]46-47计算线性方程的回归系数a和b,求得q个不同老化试验温度下速率常数ki=-2.303bi和试验常数Bi=10ai。
对q个老化试验温度下的Bi取平均值,计算如式(5)所示:
(5)
对式(2)进行对数变换,将速率常数公式变换为式(6)所示的直线关系式:
W=C+DZ
(6)
式中:W=lgk,C=lgA,D=-E/(2.303R),
Z=T-1。

2.4 统计分析及模型相关性检验
经验常数α确定以后,需要对方程Y=a+bX和W=C+DZ进行线性相关性检验,检验方法采用r检验[6]5[9]48并对W的预测区间进行估计,得到W的标准偏差SW。
2.5 老化寿命预测方程的确定
(7)
式中:t为单侧界限。
由式(1)、式(5)和式(7),可得到某一温度下,橡胶密封条的老化程度预测方程,如式(8)所示:
(8)
在某个温度下,橡胶密封条老化程度的极限临界值为y0,可将式(8)转化为橡胶密封条老化寿命预测模型,如式(9)所示:
(9)
3 老化试验数据处理及线性相关性验证
3.1 参数计算
通过尝试法在计算机上对准则I进行计算,经过多次尝试计算,得到I值最小时的经验常数α为0.74。
运用最小二乘法计算得到393 K、403 K、413 K和423 K四个老化试验温度下的速率常数k和试验常数B,结果见表1。
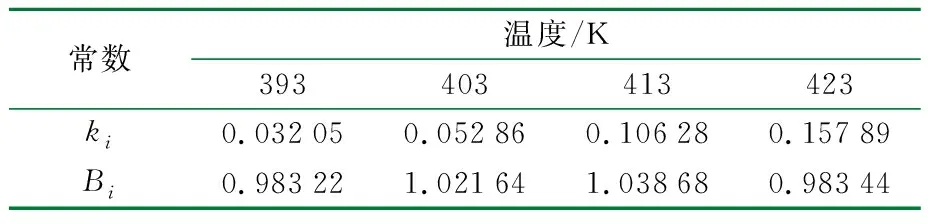
表1 不同温度下的反应速率常数k和试验常数B
从表1可以看出,试验常数Bi与实验温度T无明显的线性关系,且各老化温度下的经验常数值接近,则对四个老化试验温度下的试验常数Bi按照式(5)取平均值,得到B的估计值为1.006 75。
3.2 lg y与τ0.74的关系
将lgy与τ0.74作图,得到不同老化试验温度下lgy与τ0.74的线性关系,如图2所示。

τ0.74图2 lg y与τ0.74的关系
利用r检验计算得到图2中四条直线分别对应的线性相关系数r,计算结果见表2。

表2 不同老化温度下的线性相关系数
自由度df=q-2=2,查相关系数表可知,显著性水准为0.01时的相关性系数为0.99,从表2可知393 K、403 K、413 K和423 K计算得到的相关系数r的绝对值都大于0.99,说明图2中的lgy与τ0.74相关性显著,预测值可信。
3.3 lg k与T-1的关系
将计算值k取对数,lgk和T-1进行线性拟合,其关系如图3所示。
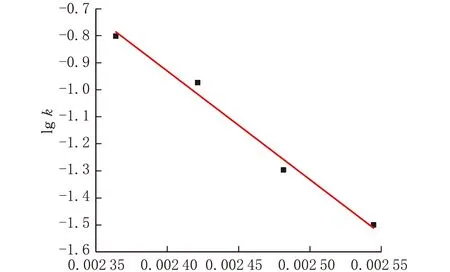
T-1图3 lg k与T-1的关系
利用最小二乘法计算式(6)中系数C和D,进行线性相关性r检验,然后对W进行偏差计算,其结果见表3。由表3可知,图3中相关系数r的绝对值大于0.99,因此可以说明W(lgk)与Z(T-1)相关性显著,预测值可信。

表3 模型参数估计值
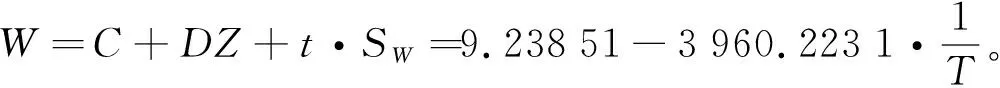
(10)
4 老化寿命预测模型验证与修正
橡胶密封条老化寿命预测模型建立之后,为了验证预测模型的准确性,需要对老化寿命模型预测值和试验值进行比较[9]52[10-11],并进行适当修正使其更准确地预测老化寿命。
选择403K、413K和423K三个温度下的试验值和预测值进行验证,其对比结果如图4所示。

老化时间/d(a)403 K
预测值曲线的老化程度y随老化时间的变化趋势与试验值各监测点的变化趋势一致,但是预测值和试验值存在一定偏差,计算出偏差Δy。将预测曲线分别向上移动Δy,则预测值经过修正后的结果如图4所示,图中经过修正的预测值拟合曲线与试验值各监测点所构成的曲线吻合很好,预测曲线得以修正。


表4 老化程度试验值与预测值的偏差
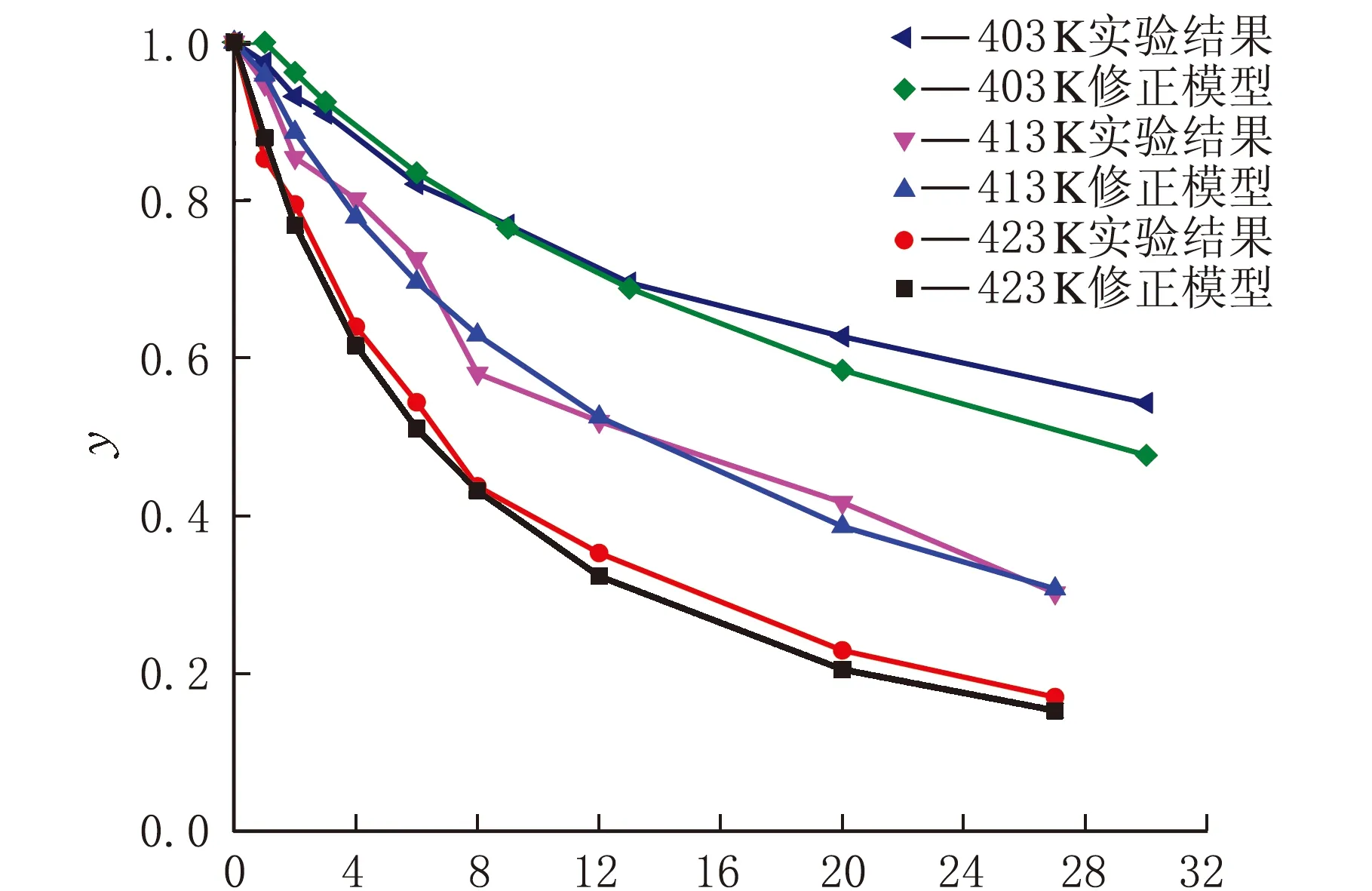
老化时间/d图5 模型修正后预测老化程度与老化时间的关系曲线
从图5可以看出,修正后的预测拟合曲线与试验监测点的曲线吻合程度较好,则预测模型修正如式(11)和式(12)所示:
(11)
(12)
根据塑料门窗用密封条国家标准GB12002—89[12]规定,在老化温度为100 ℃、老化时间为72h条件下,密封条用橡胶热空气老化性能的拉断伸长率保持率应在70%以上。塑钢窗密封条主要应用在房屋建筑上,假设在环境温度30 ℃(303K)条件下,上述橡胶的拉断伸长率保持率在70%时,根据式(12)预测的橡胶密封条的使用寿命为68.73年。本研究中老化试验仅考虑老化温度、氧气对老化性能的影响,但是塑钢窗密封条在实际应用中还要受到紫外线、臭氧以及机械力的影响,这些因素都会加速其老化,所以该模型预测的使用寿命会比实际使用寿命长。
5 结 论
(1)建立了塑钢窗用橡胶密封条使用寿命的预测模型,并对模型进行了验证和修正。
(2)模型修正后,在使用温度为30 ℃、拉断伸长率保持率为70%时,塑钢窗用橡胶密封条的使用寿命为68.73年。
