基于最优加权组合模型的煤炭消费结构预测

门东坡，王金力，何超平，张 凯

(1.国家能源投资集团有限责任公司，北京 100011；2.中国矿业大学(北京)，北京 100083)

煤炭是我国的主体能源，虽然能源结构调整的实施限制了煤炭消费的增长，但其占全国能源消费量的比重仍保持在60%左右[1-3]。随着“煤改电”“煤改气”政策的实施和散煤燃烧治理工作推进，未来煤炭消费结构将进一步向火电、冶金、建材和化工等主要耗煤行业集中。因此，客观准确地预测我国主要耗煤行业煤炭消费量，有助于促进煤炭消费结构优化和煤炭产业健康发展，对我国能源战略稳步调整和社会经济稳定运行具有重要的意义[4]。

国内外煤炭消费预测方法较多，按建模原理和建模基础，可分为单项预测模型法和组合预测模型法[5]。单项预测模型法一是根据煤炭消费量随时间变化规律建模的数学模型法，如移动平均法、回归分析法、神经网络法和灰色模型法等；二是根据煤炭消费量与经济指标之间的关系建模的经济模型法，如投入产出法、消费系数法和系统动力学法等。单项预测模型在煤炭消费量预测中的应用，王立杰[6]、谢和平[7]、Wang[8]、Zhu[9]等研究成果具有代表性，但单项预测模型往往存在一定缺陷，对复杂变动趋势的拟合结果较差。组合模型法是由两个或多个单项模型按照一定权重构建预测模型的方法。Bates[10]首次提出了以均方根预测误差值的加权平均组合预测模型。张友兰[11]和耿奎[12]认为组合预测法以最小均方误差为原则，可以充分发挥各模型优势，最大程度利用有用信息，提高预测水平。组合模型在煤炭消费预测应用方面，张金锁[5]构建的趋势外推组合模型、杨英明[13]构建的ARIMA-GM-ANN组合模型、颜筱红[14]构建的时间序列和IOWGA算子的组合模型、吕占海[15]构建的多元回归和GM(1，1)的组合模型等均能够较准确的拟合和预测全国煤炭消费量。综上，组合预测模型在全国煤炭消费量预测应用较多，但对于不同耗煤行业煤炭消费的预测研究较少，已有组合预测模型在各分行业的适用性有待深入研究。

为此，本文以灰色(GM)、差分自回归移动平均(ARIMA)、逻辑斯蒂(LOGISTIC)和人工神经网络(ANN)模型为基础构建最优加权组合模型，通过模型检验和精度分析，筛选不同行业煤炭消费量预测的最优预测模型，在此基础上对我国煤炭消费总量以及火电、冶金、建材和化工行业煤炭消费量进行预测，并分析未来煤炭消费结构的变化趋势。

1 预测模型

1.1 灰色预测模型

1.2 ARIMA模型

ARIMA(p，d，q)模型是时间序列的预测分析方法，其原理是利用差分思想对非平稳时间序列进行平稳化处理，将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型，其中p是自回归项，q是移动平均项数；d是差分次数[16]。模型数学表达式为：

Φ(B)dxt=Θ(B)εt

式中，xt(t=1，2，…，n)是数据时间序列；εt(t=1，2，…，n)是残差；B是延迟算子，Bnxt=xt-n；Φ(B)为自回归系数多项式；d为差分运算，d=(1-B)d；Θ(B)为移动平均系数多项式。

1.3 逻辑斯蒂模型

逻辑斯蒂模型(Logistic)是主要的S形函数，适合解决研究变量在开始阶段大致成指数增，后期变量增速逐渐放缓，并逐渐逼近一个极限值的问题。模型数学表达式为：

式中，t是时间变量；r是增长率；K是环境容量；yt0是原始数据序列初始值。

带入原始数据，求得逻辑斯蒂方程的解：

式(1)中K和r是影响逻辑斯蒂曲线拟合效果的关键参数，通过Marquardt非线性函数确定最优匹配的K、r值。

1.4 人工神经网络模型

神经网络由输入层、输出层和隐含层构成，输入层和输出层与外界相连，隐含层承担计算功能，其本质是通过信号向前传播和误差翻转调整学习机制，沿梯度最速下降方向训练和调整不同层神经元之间的权重和阈值，使实际输出值和期望输出值的误差均方差为最小。

1.5 组合预测模型

对式(2)用拉格朗日乘子法求解：

最优加权组合模型误差平方和为：

1.6 模型检验指标

为对比各单项模型和组合模型的拟合效果，选择相关系数(R2)进行模型的相关性检验；选择平均绝对误差(MAE)、平均相对误差(MAPE)和均方根误差(RMSE)进行模型的误差检验。

2 煤炭消费预测实证分析

2.1 数据来源

选用2005—2018全国煤炭消费总量及火电、冶金、建材和化工行业煤炭消费量为研究对象，全国煤炭消费总量数据采用《中国统计年鉴》，四大行业煤炭消费数据由各行业产品产量核算获得，如图1所示。

图1 我国历年全国及主要行业煤炭消费量(2005—2018)

根据2005—2018年全国和四大行业煤炭消费数据，各消费量ARIMA模型参数均为p=1，q=2，d=1；各消费量神经网络结构均为1×12×1；逻辑斯蒂函数K总量=40.73，r总量=-0.38；K电力=20.14，r电力=-0.34；K钢铁=6.39，r钢铁=-0.37；K建材=5.38，r建材=-0.37；K化工=6.93，r化工=-0.10。

2.2 模型验证

根据组合预测法，利用ARIMA、GM、ANN和LOGISTIC 4个单项模型组合构建全国和四大行业煤炭消费量预测模型时，理论上各消费量均可构建11个组合模型，包括6个2维组合模型、4个3维组合模型和1个4维组合模型。基于最优加权组合原理，首先利用MATLAB对各类煤炭消费量的11个组合模型进行最优权重规划求解；然后用检验指标R2、MAE、MAPE和RMSE对各组合模型预测精度进行检验，筛选获得最适合各类煤炭消费预测的最优组合模型。

2.2.1 全国煤炭消费量

对全国煤炭消费量的11个组合模型进行规划求解，组合模型最优权重系数存在单项模型系数为0的现象，致使11个组合模型中存在重复。排除重复模型后共构建GM-ANN、GM-ARIMA、GM-LOGISTIC、ANN-LOGISTIC、LOGISTIC-ARIMA 5种组合模型。

单项模型、组合模型与原始数据拟合效果如图2所示，模型检验结果见表1。单项模型中ARIMA模型R2值最高，达到0.97，同时MEA、MAPE和RMSE值最低，图2(a)中ARIMA模型变化趋势与实测值最接近，说明ARIMA模型用于预测全国煤炭消费变化趋势的单项模型最为合理。由图2(b)可知，5种组合模型拟合效果差异明显，包含ARIMA模型的组合模型拟合效果明显优于其他组合模型，说明单项模型的选取对于组合模型的影响显著；表1数据显示组合模型与实测值相关性均较好，GM-ARIMA、ANN-ARIMA和LOGISTIC-ARIMA模型R2值达到0.97，与ARIMA模型相同，但MEA、MAPE和RMSE值均小于ARIMA模型，说明组合模型拟合效果显著优于单项模型。GM-ARIMA模型较其他模型误差评价指标最低，因此选择GM-ARIMA为全国煤炭消费量最优加权组合模型。与杨英明等[13]得出最优组合模型相比拟合R2由0.90增加到0.97，MAE由3.6降低到1.2，RMSE由4.1降低到1.5，而MAPE由1.8%增加到3.1%，对于煤炭消费总量来说，MAPE为3.1%是合理的，因此综合判断得出本文所建立的组合模型具有先进性。

图2 全国煤炭消费单项模型和最优加权模型拟合效果

表1 煤炭消费单项预测模型与组合预测模型精度比较

2.2.2 火电行业煤炭消费量

对火电行业煤炭消费量的11个组合模型进行规划求解，共构建2维组合模型5个，三维组合模型2个。

单项模型、组合模型与原始数据拟合效果如图3所示，模型检验结果见表2。单项模型中ARIMA模型R2值最高，达到0.96，同时MEA、MAPE和RMSE值最低，说明ARIMA模型作为拟合火电行业煤炭消费变化趋势的单项模型最为合理。由图3(b)和表2可知，7种组合模型大致分为两类，GM-LOGISTIC和ANN-LOGISTIC的相关性和误差指标略差于ARIMA模型，剩余组合模型均优于ARIMA模型。综合来看，GM-LOGISTIC-ARIMA的R2值最高，达到0.97，MEA、MAPE和RMSE值均最小，分别为0.56、3.00%和0.82，因此选择该模型为火电行业煤炭消费量最优加权组合模型。

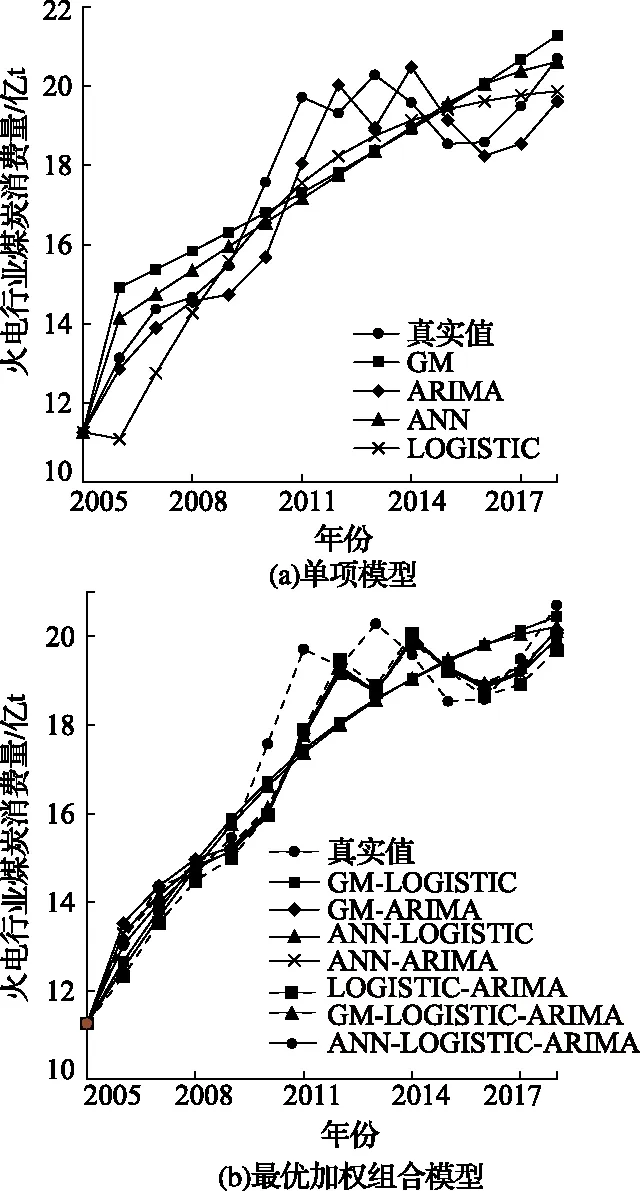
图3 火电行业煤炭消费单项模型和最优加权模型拟合效果

表2 火电行业煤炭消费单项模型与组合模型拟合精度比较

2.2.3 冶金行业煤炭消费量

对冶金行业煤炭消费量的11个组合模型进行规划求解，共构建GM-LOGISTIC、GM-ARIMA、ANN-LOGISTIC和ANN-ARIMA4种组合模型。

单项模型、组合模型与原始数据拟合效果如图4所示，模型检验结果见表3。单项模型中LOGISTIC模型R2值最高，达到0.95，同时MEA、MAPE和RMSE值最低，说明LOGISTIC模型作为拟合冶金用煤变化趋势的单项模型最为合理。由图4(a)和表3可知，4种组合模型中GM-LOGISTIC和ANN-LOGISTIC的相关性和误差指标均优于ARIMA模型，对比来看，GM-LOGISTIC的R2值最高，达到0.96，MEA、MAPE和RMSE值均最小，分别为0.23、4.01%和0.28，因此选择该模型为冶金行业煤炭消费量最优加权组合模型。

图4 冶金行业煤炭消费单项模型和最优加权模型拟合效果

表3 冶金行业煤炭消费单项模型与组合模型精度比较

2.2.4 建材行业煤炭消费量

对建材行业煤炭消费量的11个组合模型进行规划求解，共构建GM-LOGISTIC、GM-ARIMA、ANN-LOGISTIC和ANN-ARIMA 4种组合模型。

单项模型、组合模型与原始数据拟合效果如图5所示，模型检验结果见表4。单项模型中ARIMA模型R2值最高，达到0.93，同时MEA、MAPE和RMSE值最低，说明ARIMA模型作为拟合建材用煤变化趋势的单项模型最为合理。由图5(b)和表4可知，4种组合模型中GM-ARIMA和ANN-ARIMA的相关性和误差指标均优于ARIMA模型，其中ANN-ARIMA的R2值最高，达到0.96，MEA、MAPE和RMSE值均最小，分别为0.19、3.68%和0.23，因此选择该模型为建材行业煤炭消费量最优加权组合模型。

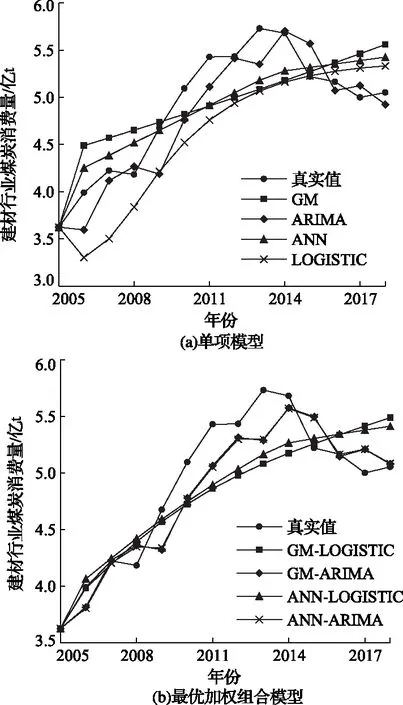
图5 建材行业煤炭消费单项模型和最优加权模型拟合效果

表4 建材行业煤炭消费单项模型与组合模型拟合精度比较

2.2.5 化工行业煤炭消费量

对化工行业煤炭消费量的11个组合模型进行规划求解，共构建GM-LOGISTIC、GM-ARIMA、ANN-ARIMA、LOGISTIC-ARIMA和GM-LOGISTIC-ARIMA 5种组合模型。

单项模型、组合模型与原始数据拟合效果如图6所示，模型检验结果见表5。

表5 化工行业煤炭消费单项模型与组合模型拟合精度比较

4种单项模型R2值均达到0.99，说明各单项模型均具有较好的拟合效果，这可能与化工用煤变化趋势波动较弱有关；对比来看ANN模型误差值最低，因此ANN模型作为拟合化工用煤变化趋势的单项模型最为合理。由图6(b)和表5可知，受单项模型拟合程度较高影响，5种组合模型R2值均达到0.99，对比误差评价指标分析，ANN-ARIMA模型MEA、MAPE和RMSE值均最小，分别为0.03、1.67%和0.04，因此选择该模型为化工行业煤炭消费量最优加权组合模型。

图6 化工行业煤炭消费单项模型和最优加权模型拟合效果

3 煤炭消费量预测

利用各类煤炭消费最优加权组合模型预测煤炭消费量见表6，各类煤炭消费变化趋势如图7所示。可以看出，2020—2030年我国煤炭消费总量和四大行业煤炭消费量变化趋势差异明显。其中，全国煤炭消费总量总体呈增长趋势，但受国家能源战略规划影响，加之环境污染和碳减排等条件制约，未来全国煤炭消费总量增幅有限，预计2020年为40.51亿t，2030年达到41.67亿t；火电耗煤总量总体呈增长趋势，但因光伏、风能等新能源对传统火电替代效应逐渐凸显，限制了火电煤耗的增长，预计2020年为21.06亿t，2030年达到22.10亿t；冶金和建材耗煤总量总体呈稳定趋势，2020年分别为6.5亿t和5.11亿t，2030年分别达到6.60和5.04；化工行业煤炭消费呈较快增长趋势，受煤炭清洁转化技术日益成熟和地方煤炭就地转化政策的影响，未来10年化工行业煤炭消耗将保持较高速增长，预计2020年为3.06亿t，2030年达到3.78亿t。

图7 煤炭消费预测变化趋势图

表6 2019—2030年全国和四大行业煤炭消费预测亿t

3 结 论

1)最优加权组合模型充分利用单项模型所反映的有效信息，弥补单项模型的缺陷，相关系数、平均绝对误差、平均相对误差和均方根误差等检验指标均优于单项模型，适合我国煤炭消费总量和主要行业煤炭消费量的预测分析。

2)根据2005—2018年煤炭消费数据，分别构建了权重为(0.32，0.68)的我国煤炭消费总量预测模型GM-ARIMA；权重为(0.28，0.14，0.58)的火电行业预测模型GM-LOGISTIC-ARIMA；权重为(0.40，0.60)的冶金行业预测模型GM-LOGISTIC；权重为(0.32，0.68)的建材行业预测模型ANN-ARIMA；权重为(0.79，0.21)的化工行业预测模型ANN-ARIMA。

3)基于最优加权组合模型，预测未来我国煤炭消费总量和火电行业消费量呈小幅增长趋势，2030年分别达到41.67亿t和22.10亿t；冶金和建材行业消费量呈稳定趋势，2030年分别达到6.60亿t和5.04亿t；化工行业消费量呈快速增长趋势，2030年达到3.78亿t。