一类广义三阶KdV方程的动力学分析和精确解

李雪霞，刘汉泽

(聊城大学 数学科学学院，山东 聊城 252059)

0 引 言

本文研究一类广义三阶KdV方程

(1)

其中u=u(x,t),ai(i=1,2,3)是任意常数，方程(1)既可以表示在重力作用下的浅水中的长波运动，同时也是研究量子力学和非线性光学的一个重要模型[11-13]。2020年，李奇芳将方程(1)转化为了多个简单的常系数高阶微分方程，然后通过求解转化后简单的微分方程进而得到了方程(1)的精确解。本文中，作者将利用动力学系统方法得到方程(1)的分岔和相位图，并对在不同区域下时方程的分岔和相图进行探讨，最后给出了系统孤立波解、周期波解的显式参数表示。

1 行波变换与首次积分

在本节中，通过将方程(1)转换为平面动力系统得到方程的首次积分，然后利用首次积分方法研究了参数空间中矢量场的所有的分岔和相位图。

为了求方程(1)的行波解，我们设

u(x,t)=u(ξ),ξ=x-ct，

(2)

其中c为传播波速，我们将式(2)代入方程(1)中，得到

(3)

对(3)进行积分得

(4)

且(4)式等价于下列二维系统[14-15]

(5)

则(5)式有首次积分

(6)

其中h是任意常数。

在下文中，我们将研究行波解的分岔和相位图，并给出有界行波解的所有可能的精确显式参数表示。

2 方程分岔与相位图

(7)

(8)

2.1 情形1：当a2>0 时

2.2 情形2：当a2<0时

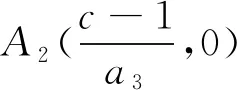
图1 当a2>0 时的相图

3 广义三阶KdV方程的精确解

在本节中，利用平面动力系统(5)和第一积分H(u,y)进行计算，给出在图1和图2中给定的参数条件下方程(1)的显示行波解。

3.1 当a2>0 时

(i) 设a1>1,c>1,且a3<0时，我们考虑如图1(a)所示的情况,令H(u,y)=h,则式(6)可以写为

(9)

图2 当a2<0 时的相图

利用上述公式(9)可以得到系统(5)的第一个方程即

(10)

求解(10)式可得方程(1)的行波解如下

(11)

(ii) 设01,且a3>0时,我们考虑如图1(f)所示的情况,令H(u,y)=h,则式(6)可以写为

(12)

利用上述公式(12)可以得到系统(5)的第一个方程即

(13)

求解(13)式可得方程(1)的行波解如下

(14)

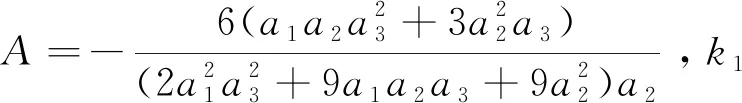
3.2 当a2<0时

(iii) 设a1=1,c>1,且a3<0时,我们考虑如图2(m)所示的情况,令H(u,y)=h,则式(6)可以写为

(15)

利用上述公式(15)可以得到系统(5)的第一个方程即

(16)

求解(16)式可得方程的如下孤立波解

(17)

其中k2是任意常数，其中u1为图2(m)中选取的研究轨线与x轴的交点，且满足u1<0。

(iv) 当a1=1,c>1,且a3>0时，我们考虑如图2(o)所示的情况,令H(u,y)=h，则式(6)可以写为

(18)

利用上述公式(18)可以得到系统(5)的第一个方程即

(19)

求解(19)式可得方程的如下光滑周期波解

(20)

4 结语

本文利用动力系统方法研究了一类三阶KdV方程在不同区域下的所有分岔和相位图，然后给出了该方程的光滑孤立波解、光滑周期波解等4个精确解，并给出了它们的精确表达式，这些精确解是新的，可能有助于解释一些实际的物理问题。