轮腿式火星探测机器人的多目标协同控制
2021-03-28孙筵龙何俊邢琰
孙筵龙,何俊,* , 邢琰
1.上海交通大学 机械与动力工程学院, 上海 200240 2.北京控制工程研究所, 北京 100190
火星环境对人们来说复杂而又未知,火星表面存在大量土壤松软区域、陡坡及各种未知障碍物[1]。这些恶劣的环境对火星车的机械结构和控制系统都提出了新的挑战和要求,众多学者提出了多种火星车方案。美国先后开展了4次火星探测任务,发射的火星车均采用摇臂转向架式悬架结构[2],该类型的火星车对地形具有良好的通过性;哈尔滨工业大学有关学者提出了一种轮步复合式移动系统构型,提高了火星车对复杂地形的通过性[3]。随着火星探测任务的深入,为了进一步提升火星车对火星各种地形的适应性,众多学者深入研究了火星车的主动调节能力,提出了多种轮腿主动悬架式机器人。加拿大研究人员研发了一种四轮腿机器人MHT[4],能够实现对机器人车体姿态的主动调节;德国研究者设计了一种新一代的火星车SherpaTT,具有轮腿主动悬架结构,能够主动适应复杂地形[5];中国的有关研究人员基于Stewart平台开发了一款四轮腿机器人BITNAZA[6]。轮腿式机器人综合了腿式机器人和轮式机器人的优点,该类机器人具有高机动性、适应环境强等特点,能够实现对地外行星的大范围巡视,具有跨越大障碍物的能力。轮腿式机器人除了具有轮式行进和腿式行进的步态外,还具有其独特的多种步态形式,以此来适应复杂多变的环境,如:文献[7]中基于腿部主动悬架的轮式行进步态,这种步态形式发挥了轮式行进的高机动性和腿部对环境的主动适应性;文献[8]中的“狗刨”式步态,该步态在车轮陷入软土时,能够摆脱困境,避免下陷。具有轮腿式主动悬架结构的火星车,成为未来火星探测研究发展的趋势。
探测机器人引入轮腿式主动悬架,提高了机器人对不规则地形的自适应能力和运动的稳定性,但同时也给控制带来了新的挑战。面对未知的地外天体环境,轮腿式机器人在行进中的稳定性难以保障,车体姿态、足端接触力、车轮的驱动力都将影响其行进的稳定性,车体姿态、足端接触力控制是保障轮腿机器人稳定行进的前提,可以避免车体不确定的振动,足端悬空、滑移及驱动力不足等问题。轮足车轮驱动力控制即过驱动问题也是轮足机器人稳定行进的研究重点。要实现轮腿机器人在不规则地形的稳定行进,多个控制的协同控制必不可少,这也带来了新的控制问题和挑战。本文主要研究轮腿机器人车体姿态、足端接触力和车体重心高度的协调控制问题。德国研究者提出了利用车体姿态和足端力实现对车体姿态和足端力调整的控制方案,并在SherpaTT机器人上实施了控制方案,提高了SherpaTT机器人对地形的通过性及驱动力的稳定性[9];日本有关学者基于ZMP(Zero Morment Point)点对六轮腿机器人提出了一种车体姿态调整的控制方案,提高了六轮腿机器人运动的稳定性[10];日本研究者在Hydrover-II机器人上实施了车体重心加速度和车体姿态协同控制的控制方案[11]。
轮腿式机器人的多目标协同控制包括身体姿态、足端接触力及稳定性控制3个方面。姿态对无固定基座机器人的运动能力有较大影响,姿态的不确定变化严重限制其运动能力。文献[12]针对卫星的姿态控制问题,提出了基于机器学习的姿态控制算法;文献[13]提出了基于PID和逻辑模糊的姿态控制策略;在文献[14]中提出了基于卡尔曼滤波的自适应姿态控制算法;文献[15]针对小型无人直升机姿态控制提出了基于增强学习的飞行控制算法。由于在深空探测任务中可以使用的CPU资源非常有限,一些在地面上实验效果很好的智能控制算法并不能应用于火星车控制。因此,研究基于少量数据处理和简单计算的姿态控制算法,是实现有限资源下火星车姿态跟随控制的关键。
在执行火星探测任务时,火星车经常会在不规则的复杂路面上行走,火星车的足端接触力会随着地形随机变化,这会使火星车足端受力不均,甚至会有车轮悬空的情况。火星车将会产生动力不足、侧滑、轮子受损等问题。阻抗控制被广泛应用于解决恒力跟踪问题,能够有效提高机器人在复杂环境运动中的鲁棒性。文献[16]提出了2种基于阻抗控制的自适应力跟踪控制框架,并在一个七自由度机械臂上实现了力的跟踪控制;文献[17]采用基于模糊自适应阻抗控制,实现了高空幕墙安装机器人末端接触恒力控制;文献[18]提出了一种非结构环境下基于自适应变阻抗的力跟踪控制策略,实现了埃斯顿ER16机器人在非结构环境中的力跟踪控制;文献[19]提出了单神经元自适应 PID 的机器人恒力控制自适应算法,实现了KUKA 工业机器人的力跟踪控制;文献[20]针对机器臂捕获空间未知物体,提出了鲁棒自适应力跟踪阻抗控制算法。针对火星车在执行探测任务时遇到由于足端接触力受力不均而引起的车体驱动力不足、轮子易损和侧滑等问题,提出了基于阻抗控制算法的机器人足端恒力接触控制算法。
稳定性是轮腿式机器人顺利执行任务的前提和基本要求。近年来众多稳定性的评价指标被提出,如:文献[21]提出的ZMP稳定性判据,ZMP点是机器人所受合力矩为零的点,若ZMP点位于机器人支撑多边形内则机器人处于稳定状态,反之亦然;文献[22]详细阐述了能量法判别机器人稳定性的原理;文献[23]提出了力角法,即施加在底座上的合力和在低速假设下的倾覆轴法向之间的最小角度,来分析机器人的稳定性;文献[24]提出了机器人三维空间内的稳定性判别,该判别法可应用于不规则的地形环境。对轮腿式机器人在不规则路面行走的稳定性进行研究,分析其ZMP点与其支撑凸面投影几何中心的距离,验证了多目标协同控制对提高机器人稳定性的有效性。
轮腿式火星探测机器人需要在复杂、未知的环境中自主行走,目前对火星表面环境信息的认知并不充分,缺乏土壤承载能力、密实度和地形、障碍物等数据,因而要求火星探测机器人对环境和地面有较强的自适应能力。此外火星探测机器人可以利用的CPU资源非常有限,因此需要研究简单有效的控制算法,来保证轮腿式火星探测机器人对火星地形的自适应能力。本文建立了轮腿式火星探测机器人运动学模型,提出了轮腿式火星探测机器人的多目标协同控制器,包括:车体姿态控制器、腿部阻抗控制器和重心高度控制器,可实时调节腿长,并通过运动学反解模型获得期望的关节角,实现了轮腿式火星探测机器人通过不规则地形时的车体姿态跟踪控制、足端恒力接触控制和重心最优高度控制,提高了轮腿式火星探测机器人对不规则地形的自适应性和运动的稳定性;在MATLAB/Simulink和UG中搭建了非结构环境下轮腿式机器人系统仿真模型,仿真结果验证了多目标协同控制策略的有效性。
1 机器人运动学建模
轮腿式火星探测机器人由车体、4个完全相同的轮腿组成,轮子安装在腿的末端,车体上装有姿态传感器IMU(Inertial Measurement Unit),4个 足端各有一个力传感器,如图1(a)所示。每条腿有转向关节、侧摆关节、髋关节、膝关节及车轮旋转关节5个自由度,因此腿末端在三维空间中具有3个移动和一个转动自由度,每个关节均为电机驱动的旋转关节。腿部采用平行四边形结构实现髋关节和膝关节的二自由度运动,将膝关节的驱动单元放在髋关节位置,这样轮腿式火星探测机器人的重量集中于车体上,使腿部轻量化[25]。该结构提高了机器人的承载性能,减小了腿部运动的惯性。
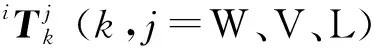
(1)

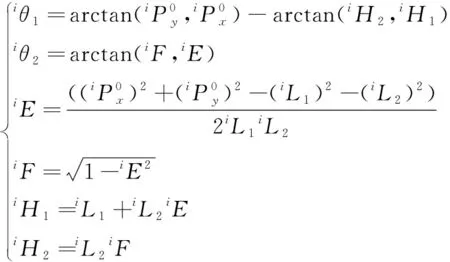
(2)


对轮腿式火星探测机器人的运动规划需要统一在车体坐标系下进行,这样有利于对轮腿式火星探测机器人系统进行整体控制,因此需进行如下运动学求解:
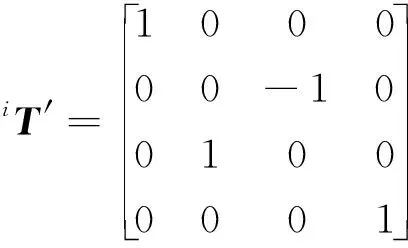
(3)
(4)
(5)
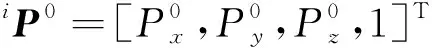
2 多目标协同控制建模
本部分详细介绍了,轮腿式火星探测机器人在不规则地形中轮式行进时,多目标协同控制系统,包括: ① 身体姿态控制器,实现车体姿态的跟随控制;② 足端恒力控制器,保证轮腿式火星探测机器人足端与火星表面的恒力接触;③ 重心高度控制器,保障腿部运动空间的安全性。利用UG和MATLAB联合仿真搭建了轮腿式火星探测机器人多目标协同控制仿真系统,如图2所示。仿真实验部分详细介绍了仿真系统的搭建。

轮腿式火星探测机器人的车体姿态控制、足端接触力控制和重心高度控制三者之间相互影响,存在耦合关系。姿态的变化及外界对足端的冲击力都将引起足端接触力的变化,此时车体姿态控制器和足端恒力控制器都将调整轮腿机器人的腿长来适应外界的变化。分析发现两者对腿长的调整趋势是一样的,如图3所示,车体姿态变化引起了足端接触力变化,此时车体姿态控制器和足端恒力控制器都将调整腿B、C伸长、腿A、D压缩,两者呈现正相关性,此外当机器人处于无阻扰控制机器人状态时此时车体姿态控制器无法发挥作用,足端恒力控制器将调整腿长实现足端恒力接触,这也避免了单纯的姿态控制引起的车体沿对角腿轴线翻滚的情况,起到了预测车体翻滚趋势的作用。为增加控制系统的稳定性和抗干扰能力在车体姿态控制加入PID控制算法,足端恒力控制器中采用阻抗控制算法。同时车体姿态控制、足端接触力控制引起了车体重心高度的变化,通过研究腿部的运动空间,形成了基于腿部危险系数的重心高度控制算法,其综合考虑了车体姿态控制、足端接触力控制引起的轮腿机器人腿部运动空间的变化,如图3所示,重心高度的控制不会对车体姿态和足端接触力产生影响。各控制算法在下文进行了详细阐述。


2.1 姿态控制
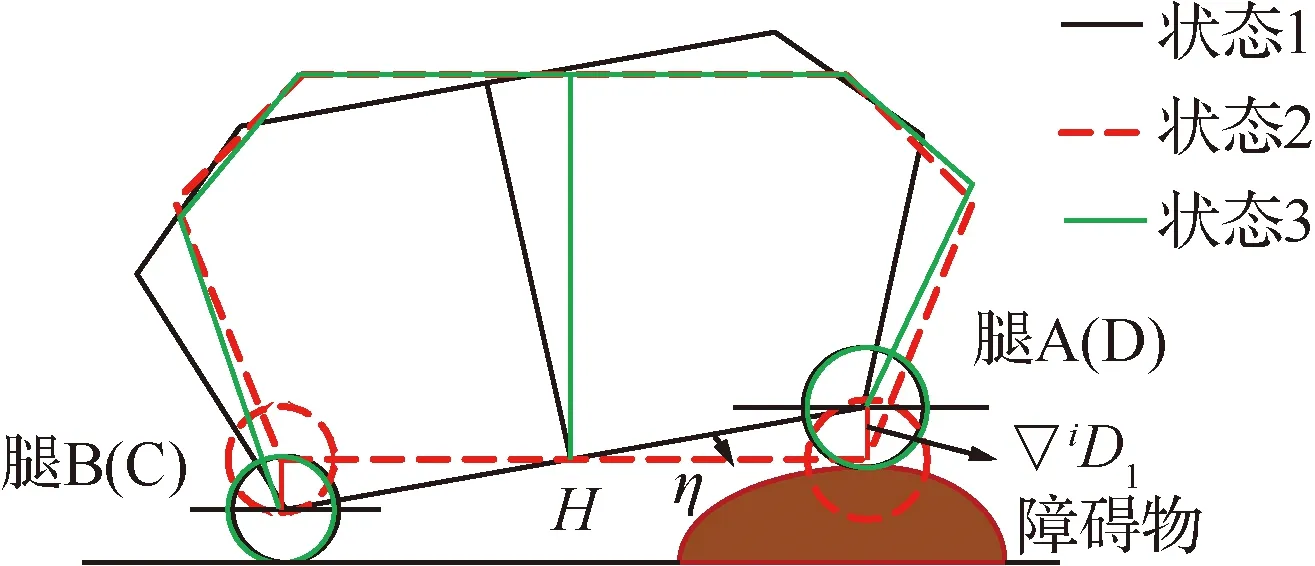
轮腿式火星探测机器人在不规则的复杂地形行进时,身体姿态总是随着地形随机变化。地形对车体姿态的影响严重限制了机器人的运动能力,甚至会出现机器人翻倒的危险,使机器人丧失执行任务的能力和损坏元器件。为了实现机器人姿态跟随控制,提高机器人对地形的通过性,基于机器人在地形中所处的状态,建立了姿态调整的运动学模型。车体俯仰角随着地形发生变化时,车体的调整过程,如图4所示。
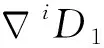
(6)
与上述分析过程相似,可以得到车体翻滚角γ发生变化时,进行姿态调整所需的理想腿长调整量为
(7)
综上可得车体姿态角η、γ发生变化时腿长补偿量为
(8)
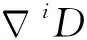
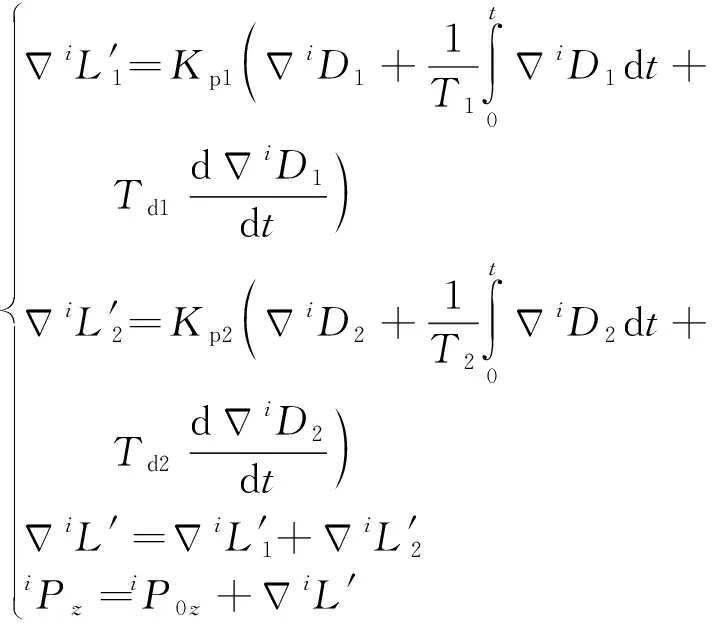
(9)
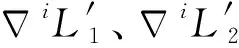
2.2 接触恒力控制
轮腿式火星探测机器人在平坦的火星地形上行进时,4个足端将与火星表面可靠接触且足端重力方向接触力为恒力。但轮腿式火星探测机器人在执行探测任务时必然会遇到不规则的复杂地形,这时足端接触力将受力不均且会出现足端悬空的情况。图5(a)中轮腿式火星探测机器人在不规则地形行进时,腿B、C在火星表面上,腿A在障碍物上,腿D处于悬空状态,机器人因腿A、B、C形成的三角形支撑区域保持稳定。但这种足端受力不均甚至足端悬空情况的出现,会使机器人出现侧滑,加速车轮损伤,驱动力不足等问题,严重影响了轮腿式火星探测机器人对地形的自适应能力和运动稳定性。利用阻抗控制算法实现轮腿式火星探测机器人由图5(a)状态调整为图5(b) 状态,此时腿D与火星表面接触,实现了轮腿机器人足端与火星表面可靠接触且足端重力方向接触力iF0均匀分布。

(10)


(11)
式(11)经拉普拉斯变换可得
(12)


式(11)中需要获得足端期望接触力iFref和实际接触力iF。足端实际接触力iF由轮腿式火星探测机器人4个足端力传感器测量获得,但由力传感其采集得到的力信号中夹杂着大量的高频振荡信号。对信号处理算法进行了研究,利用一阶低通滤波算法,从原始力信号iF0中提取了可用力信号iF。
(13)
式中:fc为截止频率。
足端期望力iFref应尽可能相近,假设轮腿式火星探测机器人低速行进,只受火星重力及足端接触力的作用[9],对机器人进行整体静力分析可得
(14)

设
(15)
式(14)可写为
(16)
式中:H+为伪逆矩阵,H+=HT(HHT)-1。
为计算方便,这里取平面μ过轮腿机器人重心COG,平面μ中坐标系O′由坐标系OV绕其X轴、Y轴分别旋转γ、η角得到。因此P′c=[P′cx,P′cy,P′cz]=[0,0,0]并可由车体的当前姿态求解iP′=[iP′x,iP′y,iP′z]。
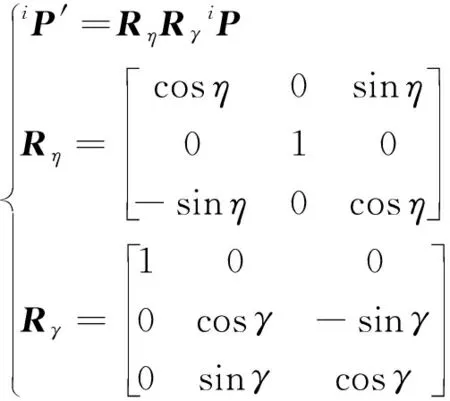
(17)
式中:Rη和Rγ分别为车体坐标系OV绕其X轴、Y轴分别旋转γ、η角的旋转矩阵。由此式(16) 得以求解。
2.3 重心高度控制



(18)
3 仿真验证
3.1 仿真工况描述
为验证多目标协同控制系统的有效性,在MATLAB/Simulink和UG中建立轮腿式火星探测机器人联合仿真模型,实现了MATLAB/Simulink与UG间的信息交互。火星地形地貌的典型特征[1],如表1所示,在UG中建立轮腿式火星探测机器人机械系统和地形环境,如图7所示,可以从中测量获得机器人在轮式行进时足端在重力方向触力iF0和车体姿态角η、γ。文献[26]建立了MGM2011模型,能够较为准确的估算出火星重力的分布,火星重力加速度约为3.6~3.8 m/s2,该模型在月球和地球上得到了验证,本文选取火星重力加速度为gmars=3.7 m/s2。在MATLAB/Simulink中搭建多目标协同控制系统,实现车体姿态控制算法、足端恒力控制算法和重心高度控制算法。本部分进行了3次仿真实验,分别为:① 无多目标协同控制;② 多目标协同控制;③ 多目标协同控制-无重心高度控制。并采集和分析了3次仿真实验中的车体姿态角γ、η,足端接触力iF,腿部危险系数σ和ZMP点等数据。

表1 仿真环境典型地形参数

仿真过程中,轮腿式火星探测机器人4个腿的布置方式为关于车体坐标系OV的X-Z平面和Y-Z平面对称,因此4个足端期望接触力为iFref=mgmars/4;车体理想的俯仰角η=0°,翻滚角γ=0°;运动规划模块给定轮速iω=4 rad/s(i=A, B, C, D),初始足端位置iP0;轮腿式火星探
测机器人依次通过障碍物1、障碍物2、障碍物3、障碍物4,仿真持续时间为55 s。为分析轮腿式火星探测机器人在运动过程中的稳定性,将4个足端点投影到平面μ中,4个足端投影点形成的多边形区域,足端点记为A、B、C、D,面积记为S。轮腿式火星探测机器人在平坦的火星地形上行进时,其ZMP点记为ZMP0=(0,0),4个足端投影点形成的多边形区域面积记为S0。在坐标系O′中计算轮腿式火星探测机器人ZMP点:
(19)
(20)
(21)
式中:(Xzmp_t,Yzmp_t)为t时刻轮腿式火星探测机器人ZMP点坐标;dt为t时刻轮腿式火星探测机器人ZMP点到ZMP0的距离。
3.2 仿真结果分析
轮腿式火星探测机器人车体姿态角η和γ的变化曲线如图8所示,足端接触力iF的变化曲线如图9所示。从实验结果可以看出多目标协同控制有效改善了车体姿态角的大幅度变化和足端接触力iF较大的分布不均等问题,使得车体姿态角η和γ分别在-3.78°~+3.48°、-3.66°~+2.47°范围内小幅度波动,各足端接触力iF在500~1 000 N中小幅度变化,由此可得多目标协同控制实现了车体姿态的跟随控制,足端接触力的恒力控制,提高了轮腿式火星探测机器人在不规则地形中的自适应能力。重心高度控制减小了腿部运动危险系数,27 s无重心高度控制时轮腿机器人由于D腿腿部危险系数σ过大,使得机器人停止运动,而多目标协同控制有效避免了该问题,使轮腿机器人正常行进,如图10所示,此外在0~4 s重心高度控制,消除了足端恒力控制器中一阶低通滤波器的延迟特性引起的腿部危险系数σ的变化,由此可得重心高度控制保障了轮腿机器人腿部运动的安全性,提高了其对复杂地形的自适应能力。在无多目标协同控制和多目标协同控制中,面积S最小值时,分别记足端点为A′、B′、C′、D′和A″、B″、C″、D″,面积S为S′和S″;dt最大时,分别记dt为dt1和dt2,ZMP点为ZMP1和ZMP2,此时以坐标原点O′为圆心dt1和dt2分别为半径作圆1与圆2;因此轮腿式火星探测机器人在运动过程中其ZMP点分别在圆1和圆2中变化,如图11所示。经计算S′=0.96S0,dt1=252.82 mm,S″=0.99S0>S′,dt2=139.97 mm 试验结果的误差分析主要分为两类:① 针对仿真结果的误差分析;② 针对仿真与实际工况的误差分析。从3.2节中的仿真结果可知实施多目标协同控制后车体姿态角和足端接触力的峰值误差减小了约4倍,车体姿态角和足端接触力的标准差为 (22) 表2中MB0表示无多目标协同控制,MB1表示实施多目标协同控制。如表2所示,车体姿态角、足端接触力变化的波动大小都降低了约4倍。同时在控制过程中理论上车体的偏航角将保持为零,从图12可以看到偏航角发生了变化,但变化很小在-4°~2°范围内小幅波动,分析发现这主要是由于在控制过程中没有根据车轮与地形的接触状态对车轮运动加以控制,常用的控制方法有速度控制和力矩控制,关于车轮的运动控制问题不在本文的研究范围内,这里不在进行详述,偏航角较小的误差不会对多目标协同控制算法有效性的验证产生影响。综上可得多目标协同控制算法实施后轮腿机器人的车体姿态和足端接触力仍会产生误差,但误差较小,车体姿态角和足端接触力的峰值误差及波动大小,均有明显改善,所以仿真结果验证了多目标协同控制算法的有效性。 表2 车体姿态角和足端接触力标准差 仿真环境与实际工况存在一定的差距,主要的误差来源于运动学模型的准确性、外界不确定噪声对传感器信号的干扰、实际工况与典型地形的差别。在实物模型中,由于加工精度、机械装配等会给运动学模型带来一定的误差,这种误差可以通过重复进行试验,求取平均值的方法提高运动学模型的准确性[7];针对外界不确定噪声带来的传感器测量误差,可以使用抗干扰强的传感器和滤波算法,对于传感器和滤波算法的研究这里不在进行阐述;本文通过仿真实验验证了多目标协同控制策略对轮腿机器人在典型工况中运动的有效性,在实际的火星地形中地面承载力变化的随机性较大,但多目标协同控制算法具有一定的鲁棒性,并能充分发挥轮腿式机器人主动悬架弹性系数与刚度系数可调的优点,通过实时调节阻抗参数与PID参数来适应各种随机干扰,关于参数的实时调节不在本文的研究范围内,未来将对其进行深入研究。 从以上实验数据分析中可以看到尽管仿真结果存在微小误差且仿真环境与实际工况有所差距,但多目标协同控制算法的有效性仍得到了验证,该控制算法实现了车体姿态跟随控制和足端恒力接触控制,保障了轮腿式机器人腿部运动空间的安全性,提高了轮腿探测机器人对不规则地形的自适应能力和运动的稳定性。 1) 提出了一种基于车体姿态、足端接触力及重心高度的多目标协同控制策略,为轮足机器人在非结构环境下移动控制提供了基本依据。 2) 利用UG和MATLAB进行联合仿真,并对结果进行了误差分析验证了多目标协同控制策略的有效性,车体姿态角和足端接触力峰值误差均减小了约4倍且车体姿态角和足端接触力波动大小也减小了约4倍。 3) 未来将对轮腿机器人在未知环境中的全地形运动控制进行研究,多目标协同控制器中PID参数及阻抗参数的在线辨识及轮腿机器人过驱动问题将是未来研究的重点。


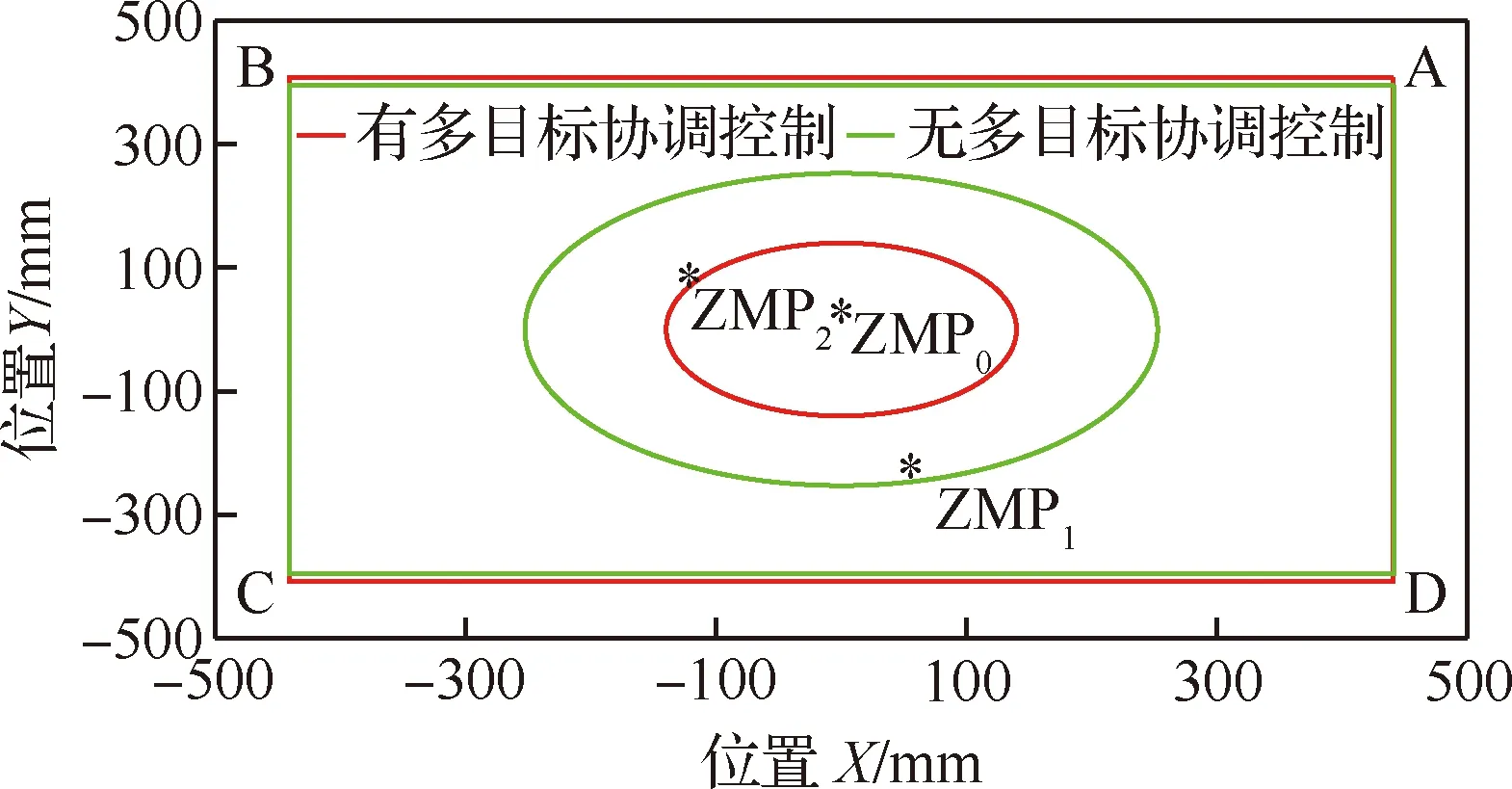
3.3 误差分析


4 结 论
