华北落叶松人工林差分地位指数模型构建

王志波,季 蒙,李永乐,李银祥,马世明,张海东

(1.内蒙古自治区林业科学研究院,呼和浩特 010010；2.兴和县苏木山林场,内蒙古 兴和 013650；3.内蒙古乌兰察布市林业科学研究所,内蒙古 集宁 012000)

森林立地是指气候、地貌、土壤及其它生物等对森林生长发育具有重要作用的环境因子总体[1]。科学地评价立地质量,准确掌握环境因子对森林生产力的影响程度,对宜林性和林木生长量进行合理预测,是开展营造林作业设计、生产潜力评估、森林抚育管理等工作的基础[2-3]。评价立地质量的方法有多种,其中,地位指数法由于简便明了,使用最为普遍[4-5],是最有效、最客观的一种方法[6]。

地位指数是指林分在基准林龄时优势木平均高度值,地位指数模型的构建主要采用两种方法,一是固定基准林龄的静态方程,另一种是可变基准林龄的动态方程[7-8]。静态方程在推导优势木树高生长曲线时,需预先确定基准林龄,并利用基准林龄时的树高(地位指数)推算其它时刻的树高；而动态方程的基准林龄是可变的,在推导优势木树高生长曲线时,选择任何一个林龄都可以得到一个相同的地位指数曲线[9]。因此,动态方程构建的地位指数模型比固定基准林龄的静态方程更加精确,更具有优势。

自1963年Clutter[10]首次将差分生长模型(projection growth models)应用于美国火炬松生长与收获预估后,差分模型被广泛应用于模拟林分生长过程[11-12]。Bailey等[13]于1974年利用代数差分法(algebraic difference approach,ADA),通过指定生长方程中一个与形状有关的参数为自由参数,构建差分方程,并建立了新西兰辐射松人工林动态地位指数模型。使用ADA法推导的差分地位指数模型,由于只设置一个自由参数,构建的地位指数曲线簇仅能满足多水平渐进极值或多形性中的一个特性[14]。针对这一问题,Cieszewski等[15]扩展了ADA法,提出广义代数差分法(generalized algebraic difference approach,GADA),并进行了详细的研究和应用[16-18]。此法在推导时设置多个自由参数,能够构建具有多条水平渐近线和多形性两个特性的位指数曲线簇[12,19],因而受到了广泛关注。

Richards方程[20]是在Von Bertalanffy生长理论方程的基础上扩展而来,具有很强的灵活性和广泛的适应性,可对单木或林分的生长规律进行很好的拟合与预测,是近代林业应用最为广泛的一类生长曲线方程[21-22]。基于Richards生长方程,童佳鸣等[23]构建了方竹枝叶生长动态模型；董晨等[24]构建了杉木胸径和树高生长模型；范阔等[25]运用改进的Richards方程构建了马尾松人工林地位指数模型；李斌成等[26]、牛亦龙等[19]分别利用ADA法、GADA法对基础理论生长方程进行推导,并构建杉木、长白落叶松人工林地位指数模型,其中,Richards方程推导的差分地位指数模型拟合效果最佳,能够更为精确地描述优势木树高生长进程。

华北落叶松(Larixprincipis-rupprechtii)为松科落叶松属的落叶针叶乔木,在内蒙古主要分布在阴山、燕山和大兴安岭等地区,是重要的山地造林树种。该树种具有耐寒、生长速度快,材质优良等特点,是重要的用材林树种,在水土保持、涵养水源、调节气候等方面也发挥了重要作用。建立华北落叶松人工林地位指数模型,科学的评估林分立地质量,对人工林经营管理和提高林地生产力等具有重要作用。本研究以阴山山地苏木山林场华北落叶松人工林为研究对象,基于Richards生长方程,分别采用ADA法、GADA法构建差分地位指数模型,并对各模型拟合情况进行全面具体的分析,筛选出适合该林区生产需求地位指数模型,用于指导实践,为华北落叶松造林、分类经营及林分质量的精准提升提供参考和依据。

1 材料与方法

1.1 研究区概况

研究区位于内蒙古乌兰察布市兴和县苏木山林场,地处阴山山脉东南段,地理坐标为东经113°38′45″～114°05′05″,北纬40°26′58″～40°42′23″,属中温带大陆性季风半干旱气候区,年均气温4.2℃,年均降水量397mm,年均蒸发量2 060mm,年均风速3.8m/s,年均无霜期110d。林场现有林地面积2.2万hm2,主要乔木树种有华北落叶松、白桦(Betulaplatyphylla)、樟子松(Pinussylvestrisvar.mongolica)、油松(Pinustabuliformis)等。华北落叶松人工林面积0.68万hm2,海拔1 500～2 300m。林下灌木主要有绣线菊(Spiraeapubescens)、山刺玫(Rosadavurica)、悬钩子(Rubussachalinensis)等,林下草本主要有菊科(Compositae)、毛茛科(Ranunculaceae)、禾本科(Gramineae)、莎草科(Cyperaceae)等。

1.2 数据来源

本研究所使用的数据为2018—2019年调查的43株华北落叶松优势木解析木数据。解析木选取时,根据研究区华北落叶松人工林分布现状,分别在不同立地条件、不同林龄、林相完整的林分内设置标准地,规格为20m×30m。设置完成后,在记录纸上画出标准地缩略图,记录地理位置、地形地貌、坡度、坡向、坡位、海拔以及造林年度、林分密度等因子。对胸径大于5cm的树木每木检尺,测量胸径、树高、枝下高、冠幅等生长指标；根据测得的数据,每块标准地挑选出1株优势木进行树干解析。表1为解析木基本信息,将43株解析木数据随机分为两部分,32株用于模型拟合,11株作为独立数据用于模型检验。

表1 优势木基本信息

1.3 模型建立

1.3.1基础模型选择

本研究选择Richards方程作为推导差分地位指数模型的基础方程。表达式为:

h=a(1-e-bt)c

(E0)

式中:h为林分优势木树高(m),t为林龄(a)；a为生长极限参数(或渐近线参数),表示生长因子的极值,是一个时间序列内的生物量上限；b为生长率参数(或尺度参数),影响曲线拐点的位置,与生长速率密切相关,起着调节生长时间的作用,此值越大,生长时间便越短；c为形状参数,决定曲线的拐点位置和形状[19-21,25];e为自然常数。

1.3.2差分方程推导

1.3.2.1一般代数差分方程(ADA)

利用ADA法推导差分地位指数模型通常包括以下几个步骤[9]:

1)选择一个生长方程为基础方程。

2)设定方程的一个参数与不可观测的立地变量X有关,即参数=X。

3)假定初始时刻值为(t1,h1),将其代入基础方程中便得到初始方程。

4)从初始方程中解出X的值,再将其解代入基础方程中去,这样我们便可以得到一个差分方程。

这种方法所推导出来的差分方程根据所选择自由参数不同,可得到单形可变渐近线或多形单渐近线两种曲线簇。本研究根据该法推导得到的差分方程如表 2所示。

1.3.2.2广义代数差分方程(GADA)

利用GADA法推导差分地位指数模型通常包括以下步骤[12,19]:

1)同样选择一个生长方程为基础方程。

2)指定方程中的两个或多个参数为自由参数。

3)提出一个与立地质量有关的变量X0,并假设自由参数与变量成各种数量关系(如,线性、反函数、二次方、指数等)。

4)将上述函数关系代入基础方程,并解出(t1,h1)时刻X0的表达式。其中,t1为指定林龄,h1为指定林龄下的优势木树高。当t1为基准林龄时,h1即为地位指数。

5)将解出的X0表达式代入基础方程中,即得到了通过GADA法推导的差分地位指数方程。

这种方法构建的地位指数模型可以满足多条水平渐近线和多形性两个属性。

参考曹元帅等[7]、赵磊等[14]、牛亦龙等[19]广义代数差分方程推导过程中参数设定方法,本研究将方程参数a和c指定为自由参数进行推导,结果如表3所示。

表2 一般代数差分方程

表3 广义代数差分方程

1.4 模型拟合与检验

使用SAS 9.0软件的NLIN过程进行模型参数的估计和拟合统计量的计算。检验模型的好坏主要依据两点:一是模型及参数的生物学涵义,二是统计指标表征的模型实际拟合效果。本研究采用回归分析中常用的决定系数(R2)、均方根误差(RMSE)和平均绝对误差(MAE)3 个统计量指标来评价模型的拟合质量。利用拟合样本计算决定系数(R2)和均方根误差(RMSE)；决定系数越接近于1,均方根误差越小,说明模型越好。利用独立检验样本数据计算平均绝对误差(MAE),数值越小说明模型预测效果越好。各指标计算公式如下:

(1)

(2)

(3)

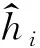
2 结果与分析

2.1 模型拟合结果

使用华北落叶松人工林优势木建模数据(表1)对Richards基础生长方程及各差分方程(表2、表3)进行拟合,结果如表4所示。6个模型所有参数的估计值均收敛较好,达到极显著水平(P<0.01),全部通过检验。模型E0的决定系数(R2)为0.891 5,均方根误差(RMSE)为0.772 6,平均绝对误差(MAE)为1.735 3；利用ADA法和GADA法推导的差分模型(E1～E5),决定系数(R2)均在0.96以上,均方根误差(RMSE)在0.86～0.96之间,平均绝对误差(MAE)在0.42以下。拟合结果表明,无论是一般代数差分方程还是广义代数差分方程,对于建模数据的拟合效果均优于基础方程,具有更好的预测能力,差分方程明显提高了模型的拟合精度。从拟合统计指标计算结果来看,模型E2最优,其次为模型E4,再次为模型E3,E5和E1,模型E0最差,初步筛选出模型E2,E4和E3为备选模型进行检验,并与基础模型对比分析。

表4 华北落叶松人工林差分地位指数模型的参数估计值及相关统计指标

2.2 模型检验

模型E2,E4,E3和E0的残差随优势木树高预测值变化情况如图1所示。4个模型的残差都随机分布在y=0两侧,模型E2,E4没有明显的变化趋势,符合等方差性假设；模型E3对较高优势木树高的预测偏大；模型E0残差随优势木树高预测值的变化呈现非线性关系。模型E0的残差波动范围在-4～4m之间,对较低的优势木树高拟合效果较好,残差绝对值随着林龄的增大呈现增大趋势。差分地位指数模型残差波动范围在-1.5～1.5m之间,明显优于基础模型,残差绝对值随林龄的增大呈现先减小后增大的趋势。模型E2,E4在预测值10m时,残差最集中,对中等的优势木树高拟合效果最好,对较高的优势木树高拟合效果相对较差。

图1 模型E2,E4,E3和E0残差图

图2 差分地位指数模型 E2,E4及E3所绘制的地位指数曲线簇

2.3 模型选择

理想的地位指数模型满足3个条件,即S形生长曲线、多形性和多条水平渐近线[7],利用备选的3个较优模型(E2,E4,E3),根据解析木数据,树高生长量在25a时开始趋于稳定,因此以25a为基准林龄,地位指数范围从7～15m,地位指数级距为2m绘制地位指数曲线簇,结果如图2所示。模型E2具备S形生长曲线和多形性,但趋向于同一水平渐近线,对低地位指数(7)的拟合效果不好,曲线形状较为平直,不符合树高随林龄的变化规律。模型E3具有多形性,但不满足S 形生长曲线和多条水平渐近线的要求,对低地位指数(7,9)的低林龄段(0～10a)树高拟合也偏小。模型E4具备S 形生长曲线、多形性和多条水平渐近线特征,是理想的地位指数模型,其表达式为:

h2=eX0(1-e-0.0313t2)(4.6150-1.002X0)

式中:h2为待预测林龄t2时的优势木树高；h1是已知实测林龄t1时的树高,当t1为基准林龄(25a)时,h1即为地位指数(7,9,11,13,15)。

2.4 优势木树高连年生长量

利用筛选的最优模型(E4)计算不同地位指数华北落叶松优势木树高连年生长量,结果如图3所示。连年生长量随着林龄的增长迅速达到最大值,然后缓慢下降。地位指数7,9,11,13,15的连年生长量达到最大时的林龄为19,15,13,10,6a,对应值分别为0.33,0.41,0.49,0.58,0.69m。优势木树高连年生长量达到最大值时的点即为地位指数曲线的拐点。

图3 不同地位指数优势木树高连年生长量

3 结论与讨论

本研究以Richards基础生长方程为原型,推导了5个与基准林龄无关的差分地位指数模型,利用内蒙古兴和县苏木山林场43株解析木数据对模型参数进行拟合,各模型拟合精度均较高。从各模型的参数估计值和拟合统计指标计算结果来看,差分模型的拟合效果均优于基础模型,这与李斌成等[26]对杉木差分地位指数模型研究,段爱国等[27]对杉木多形地位指数模型研究结果相一致。ADA法推导的3个差分地位指数模型中(E1,E2,E3),以b或c为自由参数的模型拟合结果要好于以a为自由参数的模型,这与相聪伟[9]的研究结果相同。GADA法推导的2个差分模型中,假设自由参数c与变量X0成线性关系更符合华北落叶松优势木树高生长规律。

以25a为基准林龄,地位指数级距为2m,地位指数范围为7～15m,绘制地位指数曲线簇。以b或c为自由参数的模型(E2,E3)所绘制的地位指数曲线簇中,优势木树高生长曲线为多形的,能够很好地区分开不同立地质量优势木树高生长过程,但是这类曲线簇中的曲线由于模型拥有一个共同的渐近线参数a,所有曲线都会趋向于同一条上渐近线,表现出不同立地质量优势木树高值最终是相同的,这与华北落叶松实际生长过程中立地质量越好其优势木树高渐近值就越大相违背。倪成才等[12]也认为一般代数差分法构建的差分模型仅指定一个参数为自由参数,对林分生长过程差异的解释能力是有限的。利用最优模型(E4)绘制地位指数曲线簇,并计算不同地位指数华北落叶松优势木树高连年生长量,结果表明,地位指数越大,优势木树高及其连年生长量的极值也越大,曲线的拐点也越靠近y轴。这说明在较好的立地条件下,华北落叶松优势木树高生长量在前期快速增长,并在较短的时间内达到最大值,到达拐点位置后,生长量下降的速度也越快。牛亦龙等[19]认为,这是由于立地质量较差时,林木生长的环境条件是影响优势木树高生长的主要因素,而立地条件较好时,林木自身的生物学特性是影响优势木树高生长的主要因素。

通过统计分析、残差分析和地位指数曲线簇比较,筛选出采用GADA法,以自由参数a=eX0,c=c1+c2X0推导的模型E4为最佳模型,虽然从拟合统计指标计算结果上看,它不是最好的,但利用该模型绘制的地位指数曲线簇符合S 形生长曲线、多形性和多条水平渐近线的特性,是理想的地位指数模型。利用GADA 法,合理地选择自由参数与变量的数量关系,构建动态地位指数模型,可以满足生物学和统计学两方面的要求[7],能够科学地对研究区华北落叶松人工林立地质量进行预测和评价。

本研究仅基于Richards方程进行差分方程推导,而且广义差分方程也仅设置了两种自由参数的假设,利用其它生长方程及不同自由参数数量关系的假设,所得到的模型拟合效果如何,还有待进一步研究。