基于变分模态分解与优化支持向量机的滚动轴承故障诊断
2021-03-26金江涛许子非缪维跑
金江涛,许子非,李 春,2,缪维跑
(1.上海理工大学 能源与动力工程学院,上海 200093;2.上海市动力工程多相流动与传热重点实验室,上海 200093)
滚动轴承是旋转机械中最易受损的零部件之一,因此对滚动轴承进行有效的故障诊断已成为研究热点[1]。目前,数据采集、特征提取和状态分类组成了传统故障诊断的框架。其中,特征提取的准确性和状态分类方法的可靠性会直接影响故障诊断方法的性能。为在噪声和变负载环境中提取更具代表性的故障特征,应采用精准合理的特征提取方法,这是实现故障诊断的关键[2]。
经验模态分解(EMD)、集成经验模态分解(EEMD)和变分模态分解(VMD)等时频分解算法已成功应用于轴承故障特征的提取[3]。EMD作为一种自适应信号分解算法,可对具有复杂模式的振动信号进行解耦,以实现故障特征提取,但由于包络极值点误差的积累会导致端点效应和模态混叠现象,严重影响了所提取特征的准确性和可靠性。EEMD算法由于引入了高斯白噪声,可削弱模态混叠现象,但剩余噪声易增大信号重构误差,从而影响故障特征提取的可靠性。Dragomiretskiy等[4]提出的VMD算法改善了端点效应和模态混叠现象,从而保障了故障特征提取的有效性。李华等[5]采用VMD算法和包络解调分析方法实现对滚动轴承故障特征的准确提取,研究表明基于VMD算法提取的信号具有更高的信噪比。Jiang等[6]通过优化初始中心频率的求解方法,证明VMD算法在提取旋转机械早期微弱的故障特征方面较EMD算法更有效。Li等[7]将VMD算法与神经网络算法相结合,实现对滚动轴承不同工况的智能化识别。研究表明,基于VMD-神经网络构建的智能诊断模型较EMD算法、EEMD算法和LMD算法更有效。但以上研究未考虑模态分解个数和惩罚因子对VMD算法分解精度的影响。
支持向量机(SVM)作为机器学习算法的代表之一,是一种解决小样本、非线性和高维模式的识别方法[8]。史庆军等[9]将奇异值和能量熵结合构建特征矩阵,并输入SVM分类器中进行分类。王新等[10]基于VMD算法各模态所含能量的差异,采用SVM分类器实现智能化轴承故障诊断。李莎等[11]将多重分形与SVM分类器结合,实现故障诊断。以上研究均未考虑惩罚因子与核函数对SVM分类器准确性的影响。
特征提取决定了状态分类性能的上限。为此,笔者借鉴EEMD算法的分解模式,提出VMD能量熵,保证在噪声背景和变负载下提取的故障特征有效;为避免局部最优参数会降低SVM分类器的泛化能力,基于鲸鱼算法(WOA)提出了优化SVM(即OSVM),可改善SVM分类器的诊断性能;以标准轴承实验数据为研究对象,验证VMD-OSVM方法在噪声和变负载环境下故障诊断的有效性和可靠性,为滚动轴承的故障诊断提供了理论基础和实现方法。
1 VMD算法
VMD算法是一种非递归方法,需预先设定模态分解个数,可有效抑制EMD算法和EEMD算法产生的端点效应和模态混叠现象。VMD算法将信号分解为若干本征模函数(IMF),每个IMF均为调幅-调频(AM-FM)信号,可表示为:
uk(t)=Ak(t)cos[φk(t)],k=1,2,…,K
(1)
式中:φk(t)为信号相位;uk(t)为分解得到的第k个IMF分量;Ak(t)为瞬时幅值,且为非负包络函数;K为分解个数;t为时间。
需通过以下步骤构建变分模型:先经希尔伯特变换,得到各IMF分量,进而得到信号单边频谱[σ(t)+j/(πt)]uk(t),其中σ(t)为单位脉冲函数;引入指数项来调整各IMF分量的中心频率ωk,调制每个IMF分量频谱到其相应基频带{[σ(t)+j/πt]*uk(t)}e-jωkt;根据解调信号梯度的平方L2范数估计各IMF分量带宽,则所构造的约束变分模型为:
(2)
式中:f(t)为原始信号;*表示卷积运算。
VMD算法在求解过程中通过引入惩罚因子α和Lagrange乘子λ来获得最优解。扩展后的Lagrange表达式为:
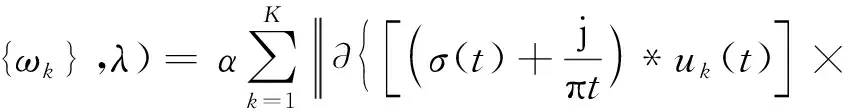
(3)
采用交替方向乘子算法(ADMM)更新uk,n+1、ωk,n+1和λn+1,得到式(3)的鞍点,从而获得最优解,将原始信号分解为K个IMF分量。
(4)
(5)
(6)
式中:τ为保真系数;n为迭代次数;ω为频率;^表示傅里叶变换。
VMD算法的流程图见图1。
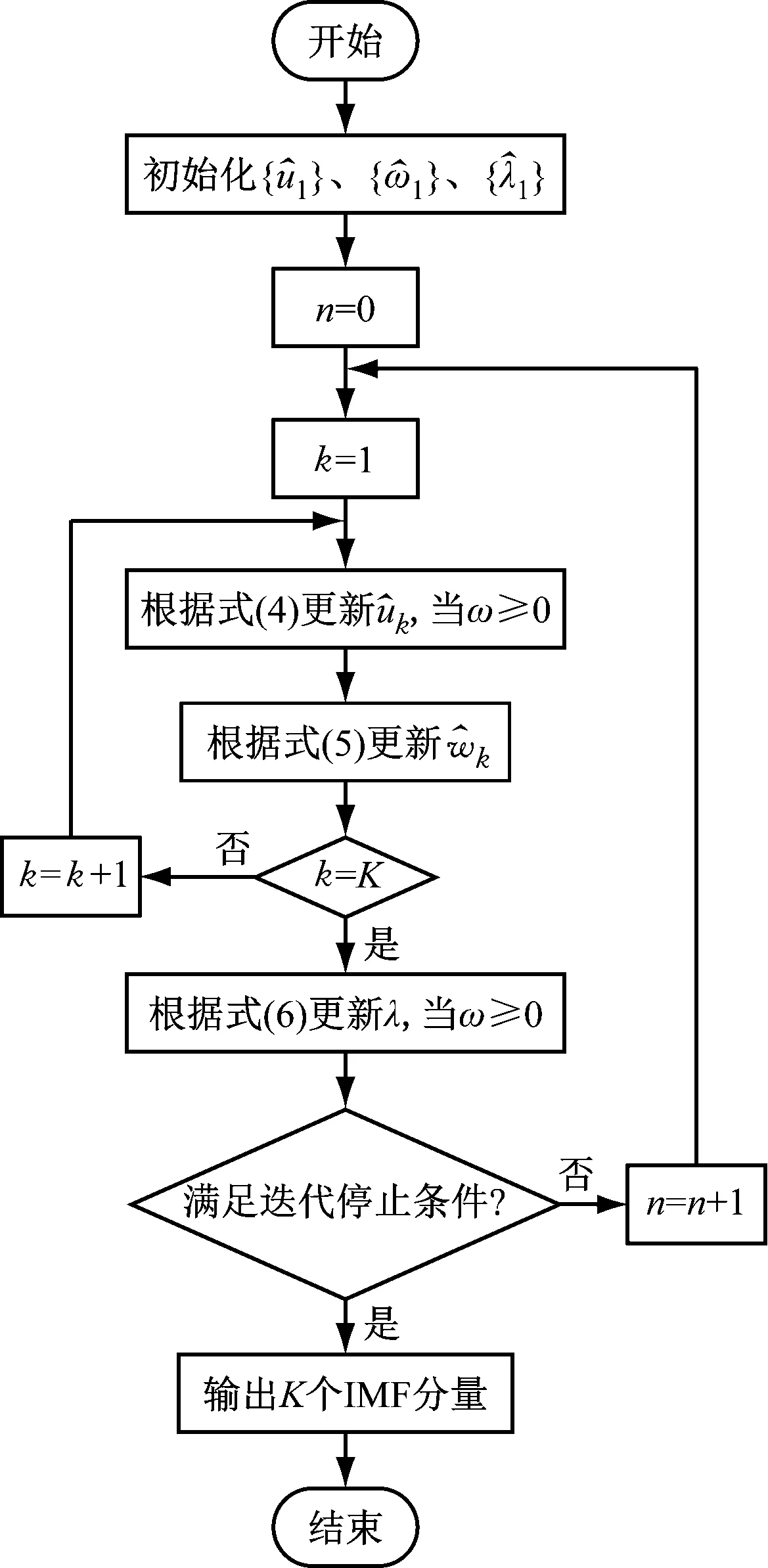
图1 VMD算法的流程图Fig.1 Flow diagram of the VMD algorithm
在求解变分模型时,IMF分量的中心频率和带宽不断更新,直至满足迭代停止条件。
(7)
式中:ε为判别精度,取10-6。
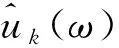
2 基于VMD算法的信号特征提取
由于VMD算法不具备递归性,需预先设定模态分解个数K和惩罚因子α。为此,借鉴EEMD算法的递归特性,确定VMD算法的分解个数K;为保证分解的准确性,惩罚因子α取值与采样频率相同[12]。
3 基于VMD-OSVM的轴承故障诊断
3.1 WOA
Mirjalili等[14]基于座头鲸随机寻猎、包围收缩和螺旋气泡网攻击策略提出了WOA,其优点在于操作简便、调节参数少和全局搜索能力强。WOA模型包括环绕捕获、泡泡网攻击猎物和猎捕搜寻3个过程。
3.1.1 环绕捕获
在捕食过程中,座头鲸确定猎物位置后将其包围,鲸鱼不断调整自身位置,鲸鱼与猎物之间的距离D为:
D=|C·X*(j)-X(j)|
(8)
X(j+1)=X*(j)-B·D
(9)
式中:j为迭代次数;X*为猎物当前位置向量,即鲸鱼最佳位置;X为鲸鱼位置向量;B和C均为系数矩阵。
3.1.2 泡泡网攻击猎物
鲸鱼以泡泡攻击猎物的数学模型为:
X(j+1)=D′eblcos(2πl)+X*(j)
(10)
式中:D′为第i条鲸鱼与猎物间的距离向量,表示当前最优解;b为螺旋状的常量;l为[-1,1]区间内的随机数。
由于鲸鱼以螺旋状游向猎物的同时也在收缩包围圈,以50%的概率在2种模式之间选择,以更新鲸鱼位置。
(11)
式中:p为[0,1]区间内的随机数。
3.1.3 猎捕搜寻
鲸鱼随机寻找猎物位置的过程模型为:
D=|C·Xrand(j)-X(j)|
(12)
X(j+1)=Xrand(j)-B·D
(13)
式中:Xrand为当前鲸鱼群中随机1只鲸鱼的位置向量。
当0≤"|B|<1时,模拟鲸鱼向猎物发起泡泡攻击的行为体现了WOA的局部搜索性能;当|B|≥1时,鲸鱼群偏离当前猎物,以搜寻更优猎物,体现了WOA的全局优化能力。
3.2 SVM理论概述
基于结构风险最小化和统计学核心VC维理论构建的SVM理论在处理小样本时具有显著优势,因此被用于故障诊断。对于传统线性分类问题,可找出一个超平面将样本分开,而对于大多数非线性问题,可引入核函数将输入空间通过映射函数映射至高维特征空间。
采用SVM理论可解决由非线性问题导致的维数灾难。常用的核函数包括线性核、多项式核、径向基核、神经网络核和双曲正切核等[15]。由于径向基核函数具有非线性映射能力强和收敛速度快等优点,故采用其作为核函数。
3.3 OSVM参数选取
通过WOA选取SVM分类器中的最佳惩罚因子和核函数,具体流程图如图2所示。
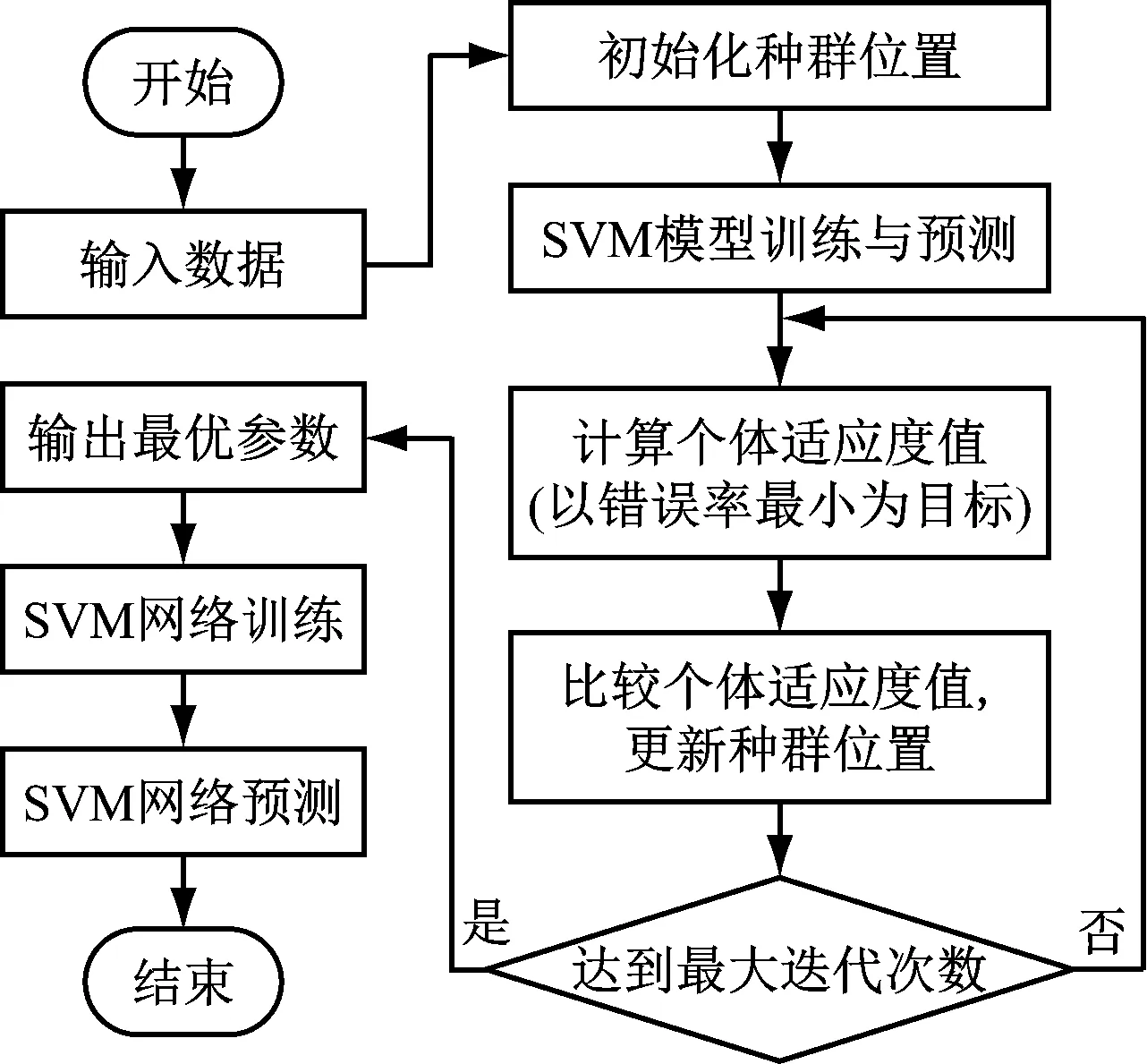
图2 OSVM参数选取的流程图Fig.2 Flow chart of selection process about OSVM parameters
3.4 故障诊断流程
对原始信号进行EEMD分解后得到模态个数,将其设为VMD算法的预设参数,并对原始信号进行分解,基于各IMF分量的能量及其能量熵构建多模态特征矩阵,将其输入SVM分类器中进行网络训练,将筛选得到的最佳参数c和g用于测试集,计算故障分类的准确率。基于VMD算法和OSVM的轴承故障诊断流程见图3。
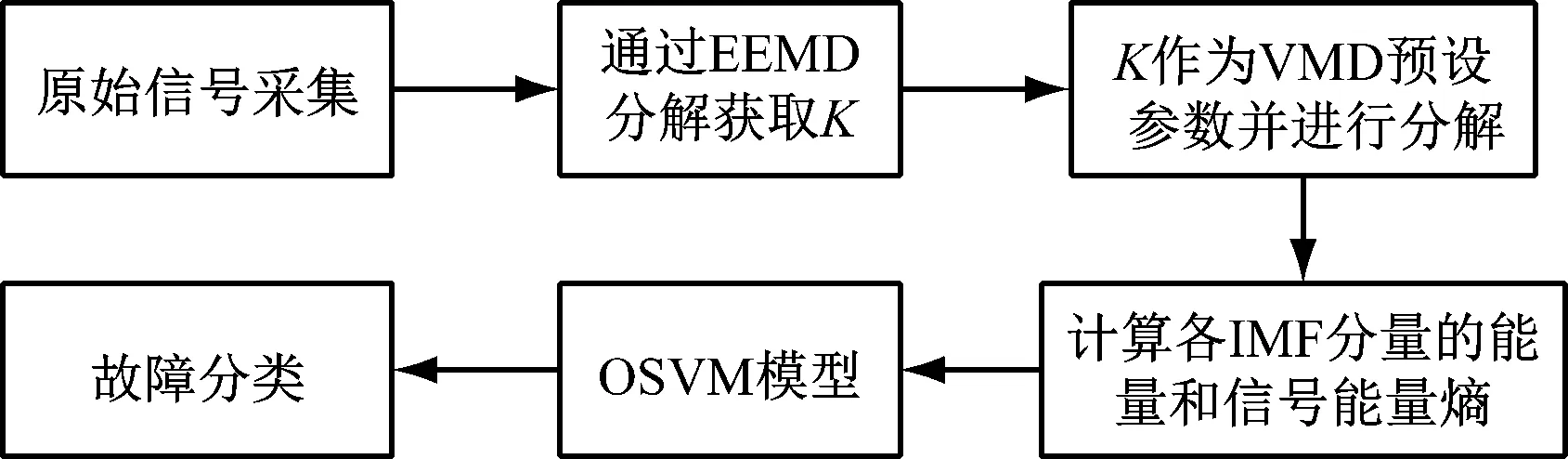
图3 轴承故障诊断流程图Fig.3 Flow chart of bearing fault diagnosis
4 实验分析
4.1 实验说明
采用美国凯斯西储大学轴承数据中心提供的实验数据[16]来验证所建方法的有效性。设置采样频率为12 kHz,轴承故障直径为0.355 6 mm,分别采集电机负载为0 kW、0.756 kW、1.512 kW和2.268 kW下轴承正常工况、内圈故障、滚珠故障和外圈故障下的信号数据。轴承内圈直径为25 mm,外圈直径为52 mm,滚珠直径为7.94 mm,轴承节径为39.04 mm,轴承厚度为15 mm,接触角为0°,滚珠数量为9。
各负载下每种工况分别采集20组信号,其中40组作为训练样本,40组作为测试样本,每组信号样本长度为4 096。分解参数K=8,α=12 000,对原始信号进行VMD分解,计算各IMF分量的能量及其能量熵,构建40×9的多模态特征矩阵,并将其输入SVM分类器中进行网络训练,训练样本的特征向量[p1p2p3p4p5p6p7p8H]见表1。由于篇幅所限,仅列举部分数据。
4.2 特征提取的可靠性验证
有效的特征提取可提升后期状态分类模型的泛化能力。为验证经VMD分解的能量熵作为特征值的有效性,计算各状态下10个样本的能量熵,见图4。在正常工况、内圈故障、滚珠故障和外圈故障下经VMD分解的能量熵平均值分别为0.562、0.977、0.831和0.503。由图4可知,轴承所处状态不同,各状态下信号经VMD分解所得能量熵不同,且未发生交叉现象,可较好地判断轴承的状态。
图5给出了各状态下样本经EEMD分解的能量熵。由图5可知,各状态下信号经EEMD分解后外圈故障与滚珠故障的能量熵存在重叠,无法准确识别轴承的状态。因此,采用经VMD分解的能量熵进行特征提取更有效。
4.3 负载对模型性能的影响
在实际工程应用中,模型应具备在变负载情况下的诊断能力。表2给出了不同的变负载情况。由表2可以看到训练集与测试集采用不同负载下的原始信号。分别采用文献[17]~文献[19]和文献[10]中所提算法、EEMD-OSVM和VMD-OSVM算法对比不同变负载情况下的诊断准确率,结果见图6。
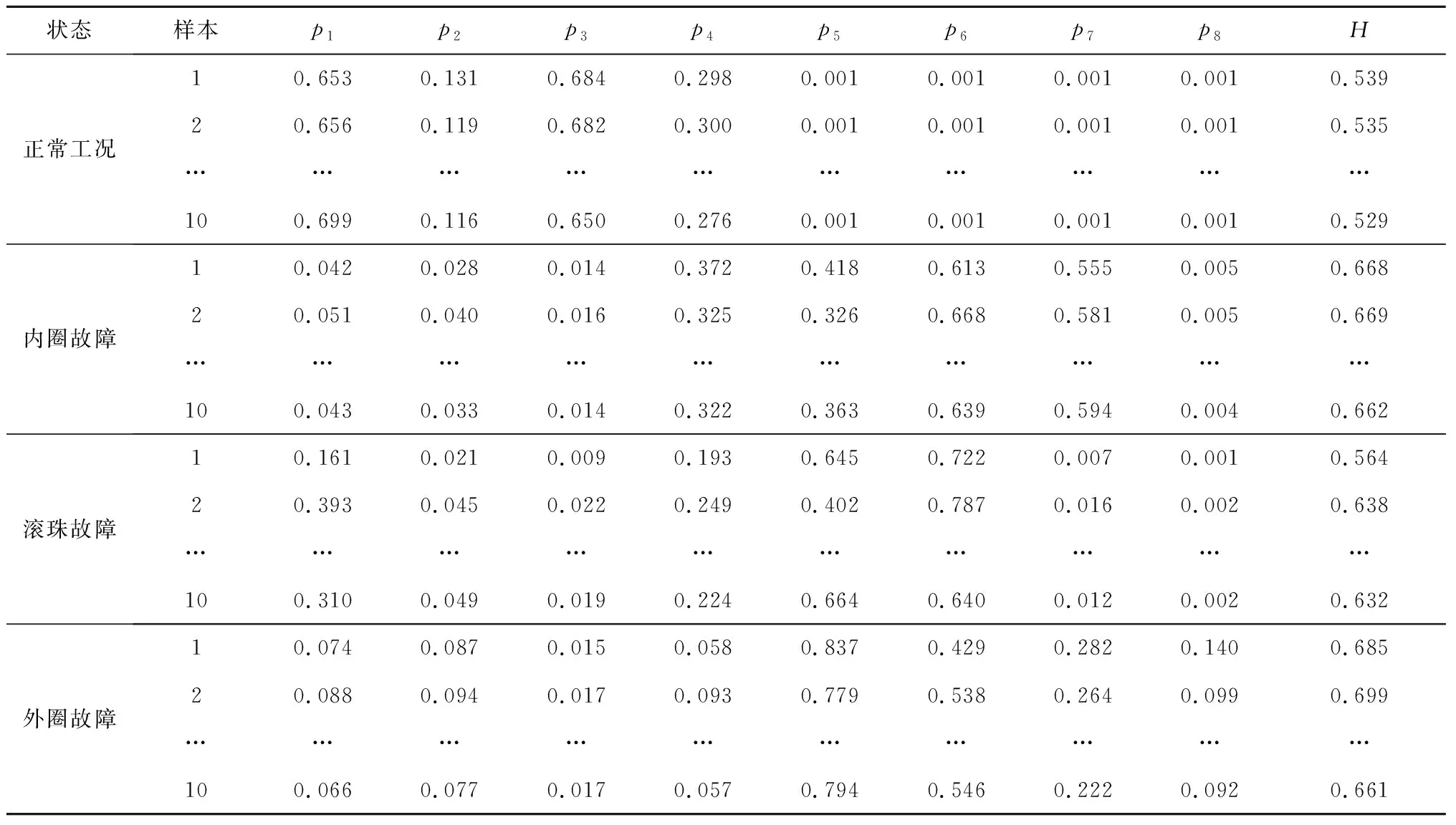
表1 训练样本的特征向量
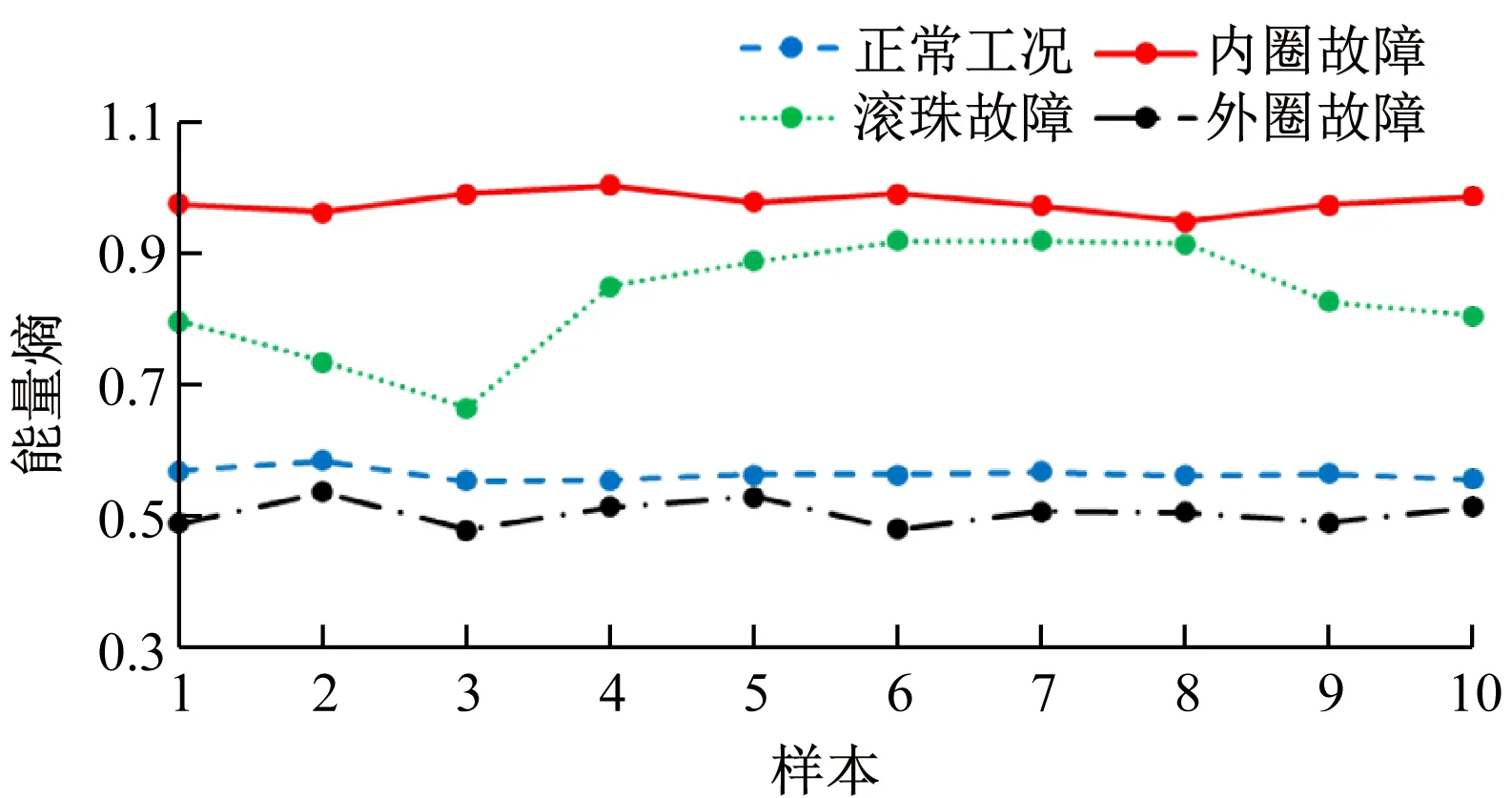
图4 各状态下样本经VMD分解的能量熵Fig.4 Energy entropy of samples decomposed by VMD algorithmat different states
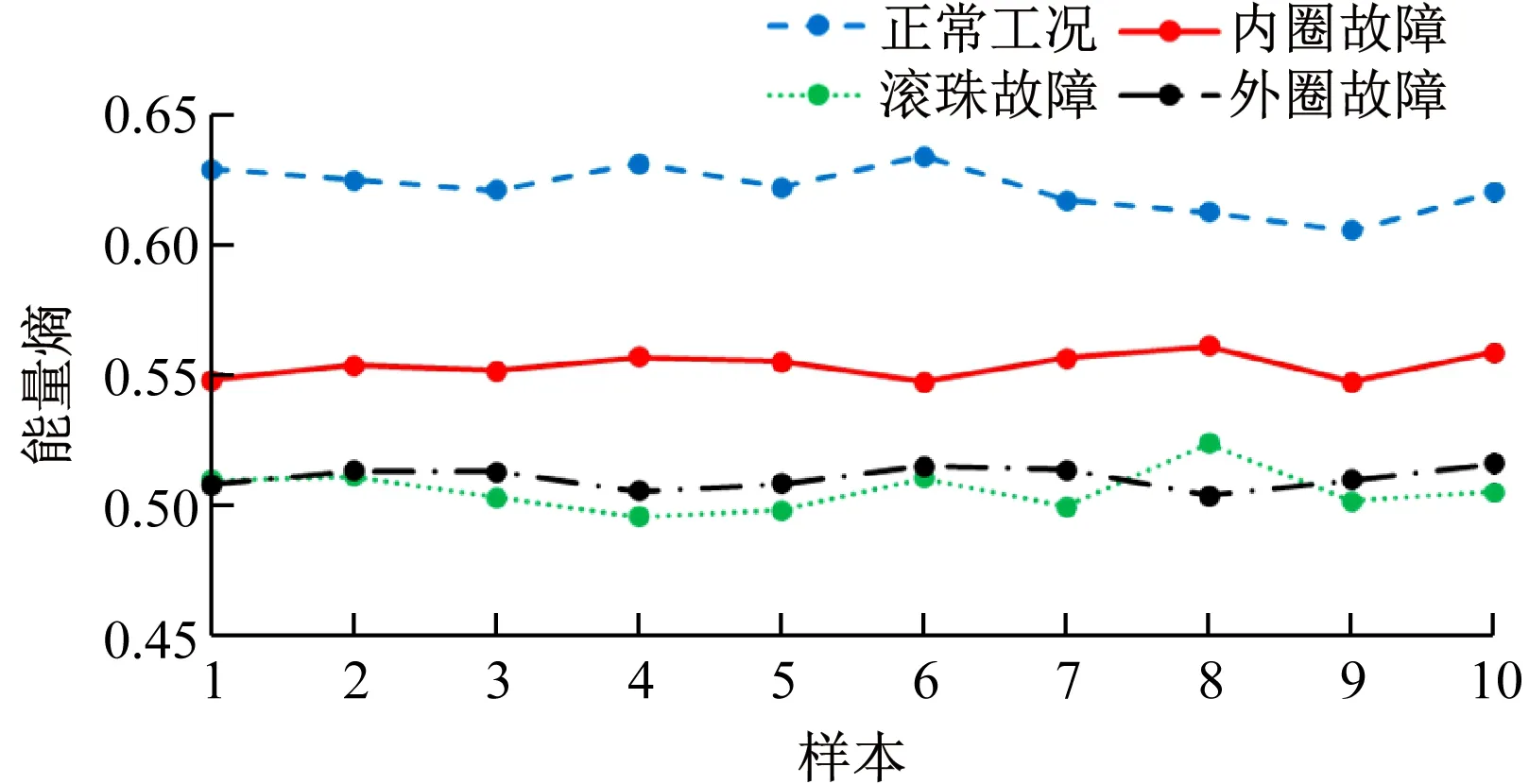
图5 各状态下样本经EEMD分解的能量熵Fig.5 Energy entropy of samples decomposed by EEMD algorithmat different states
由图6可知,采用VMD-OSVM算法时在工况3下诊断准确率为92.5%,其余情况均为100%,较文献结果[10,17-19]至少高13.8%;而EEMD-OSVM算法仅在工况1和工况4下诊断准确率稍高,其余情况几乎无法判别故障类型。综上,VMD-OSVM算法在变负载情况下具有较好的鲁棒性。
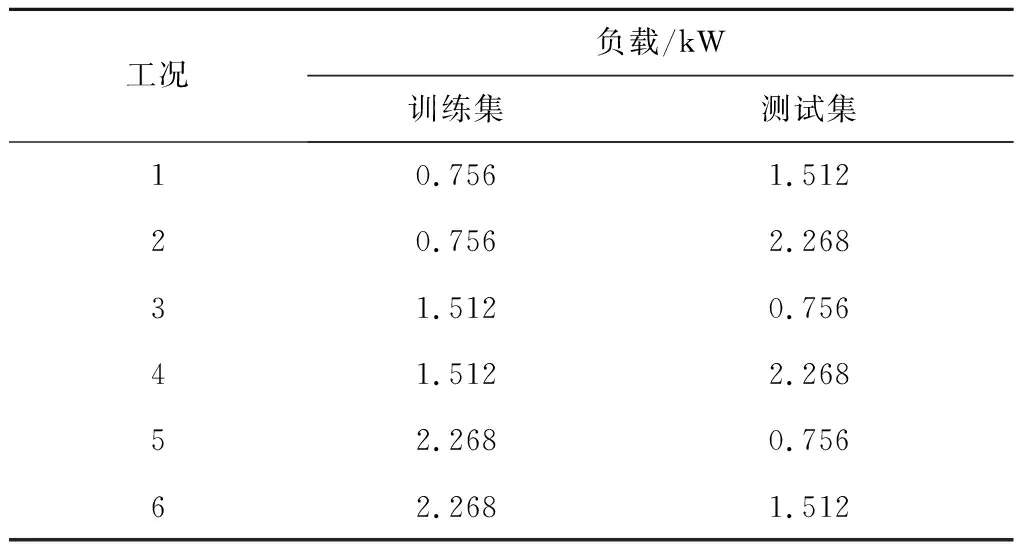
表2 变负载实验设置
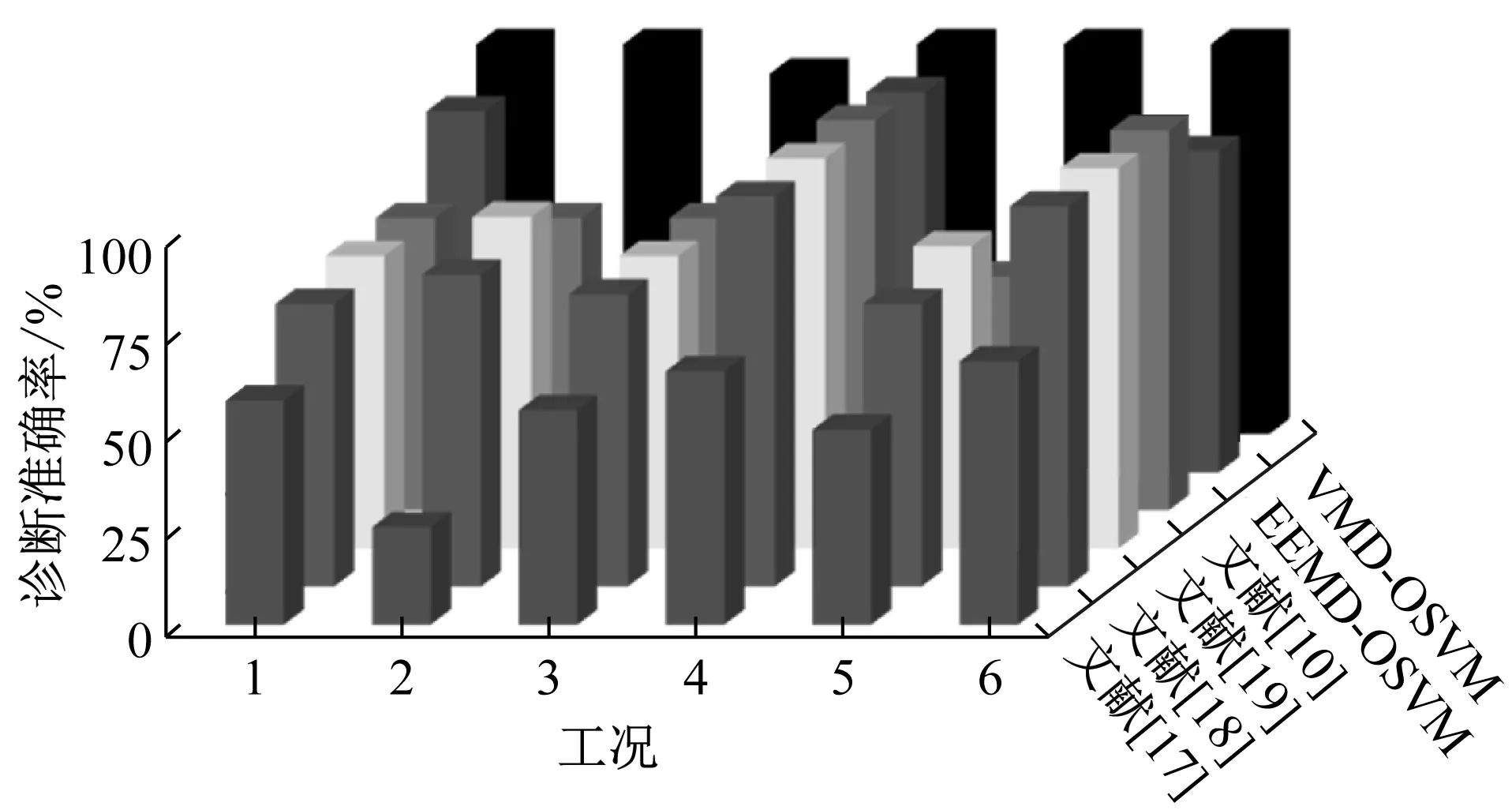
图6 变负载情况下不同算法的诊断准确率Fig.6 Diagnostic accuracy of different algorithmsunder variable loads
4.4 噪声对模型性能的影响
由于轴承所处环境复杂,无法避免噪声,为验证模型在噪声环境下的诊断准确性,在信号中加入信噪比为4 dB的高斯白噪声,以模拟真实环境。以轴承内圈故障为例,加入噪声前后的振动信号幅值如图7所示。由图7可知,加入噪声后振动信号幅值波动明显,其波动较加入噪声前波动更剧烈。
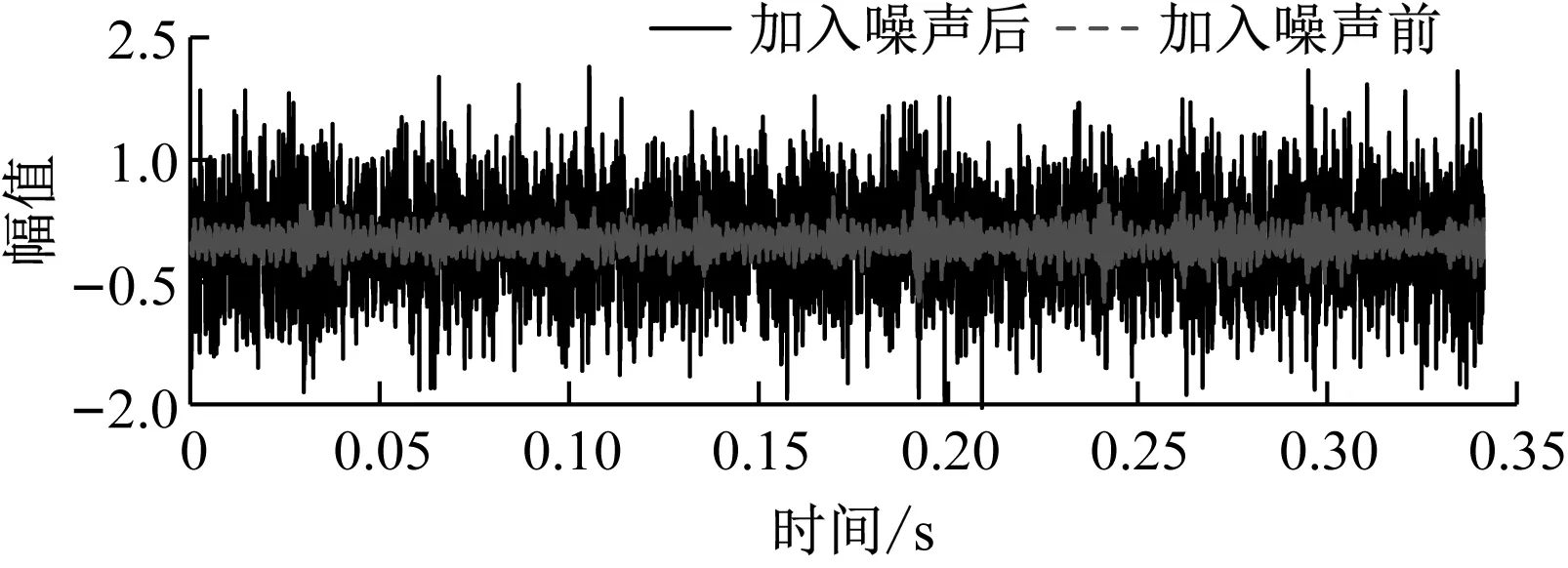
图7 加入噪声前后的振动信号对比Fig.7 Comparison of vibration signals before andafter adding noises
加入噪声前原始信号包络谱图如图8所示。由图8可知,由于该轴承信号在良好的环境下测得,因此其故障特征频率十分明显。轴承内圈故障特征频率为162 Hz,与滚动轴承结构参数所计算的故障特征频率一致。这表明原始信号在未加噪声情况下,可通过故障特征频率判别轴承故障类型。
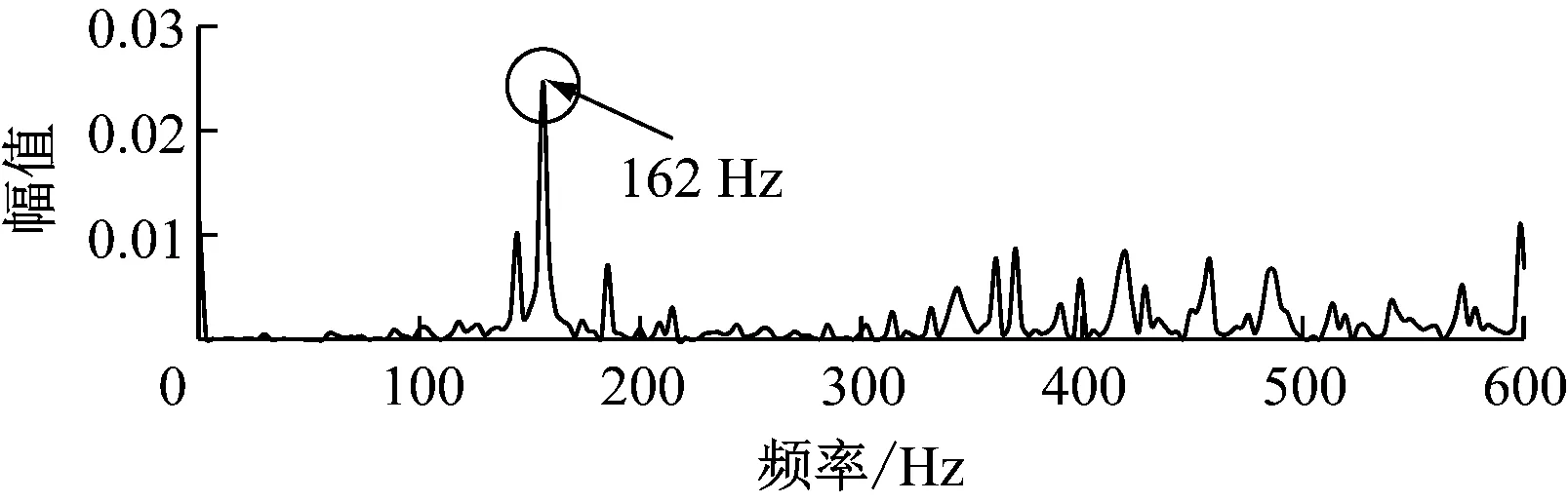
图8 加入噪声前的包络谱图Fig.8 Envelope spectrum before adding noises
加入噪声后信号包络谱如图9所示。由图9可知,轴承故障特征频率完全被淹没,因此无法通过故障特征频率判别轴承故障类型。
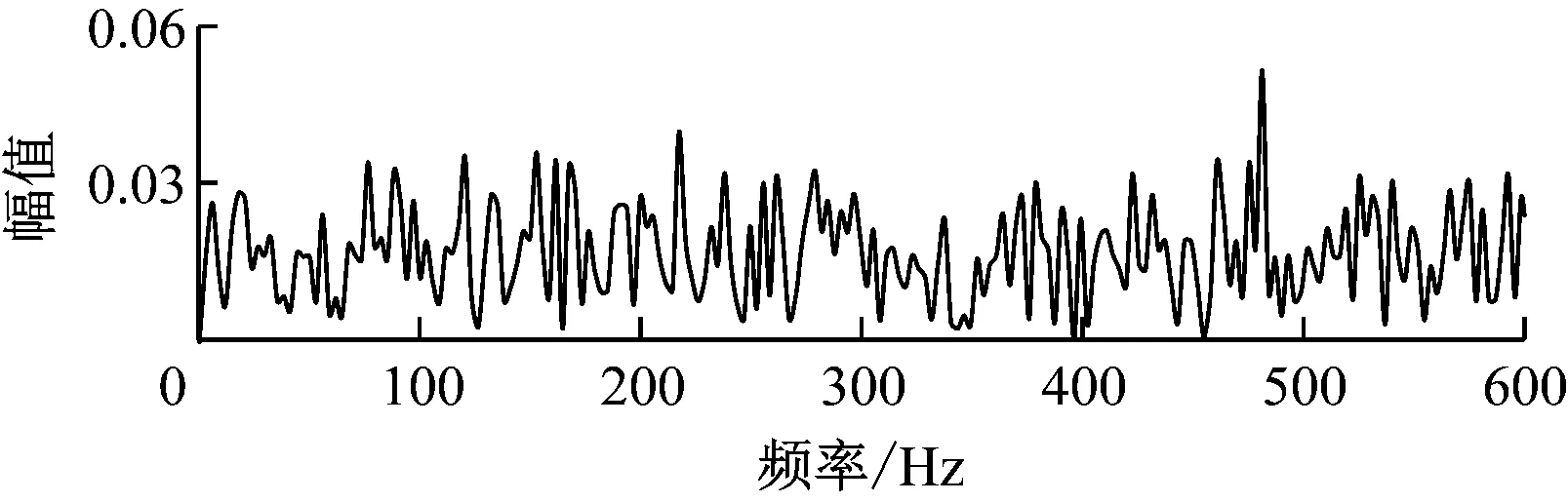
图9 加入噪声后的包络谱图Fig.9 Envelope spectrum after adding noises
为验证本文模型在噪声环境中的优势,分别采用文献[17]~文献[19]和文献[10]中所提算法、EEMD-OSVM和VMD-OSVM算法对比不同信噪比下的诊断准确率,结果如图10所示。由图10可知,信噪比为12 dB时,所提VMD-OSVM算法的诊断准确率达到99.9%,较EEMD-OSVM算法和文献[18]中算法的诊断准确率增幅分别约为10%和12.5%。信噪比为4 dB时,VMD-OSVM算法的诊断准确率仍能达到75%,远高于其他算法。与EEMD算法相比,VMD算法是更好的时频分解算法;与OSVM算法相比,GA和PSO算法优化SVM易陷入局部最优解,导致模型泛化性能较差,故障诊断准确率低。这说明同时考虑特征提取的有效性和分类器参数选取的可靠性,可提升故障诊断模型的泛化能力,因此所提VMD-OSVM算法在处理含噪信号时具有更高的诊断准确率。
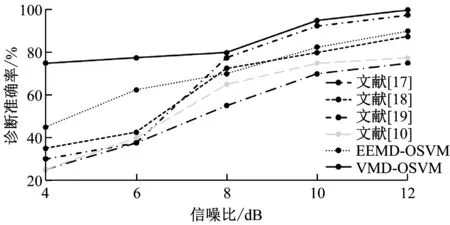
图10 不同算法在各信噪比下诊断准确率的对比Fig.10 Comparison of diagnostic accuracy of differentalgorithms at different SNR
不同算法的运行时间见表3。由表3可知,VMD-OSVM算法的运行时间为1.835 s,较文献[18]和文献[19]算法分别快39.6%和73.7%。虽然文献[17]和文献[10]运行时间较短,但由于未优化SVM分类器参数c和g,模型鲁棒性和泛化性能较差,致使其在诊断准确率方面欠佳。

表3 不同算法的运行时间
5 结 论
(1) 采用优化VMD算法与能量熵构建多模态特征值矩阵的特征提取方法优于EEMD与能量熵结合。
(2) 在变负载实验中,VMD-OSVM算法的诊断准确率相比其他算法高13.8%,体现了该算法在变负载环境中的鲁棒性。
(3) 相比其他算法,信噪比为4 dB时VMD-OSVM算法的准确率仍接近75%,在不同信噪比下均具备最高的准确率,说明VMD-OSVM算法具有较好的泛化性能。
(4) 对信号进行VMD分解后,与通过GA和PSO算法优化SVM相比,VMD-OSVM算法的运行时间更短,效率更高。
