基于Matlab与三维空间几何变换的车辆动态包络线获取方法研究
2021-03-26户攀攀刘建新蔡久凤刘志伟
户攀攀 刘建新 蔡久凤 刘志伟
1西南交通大学机械工程学院 成都 610031 2西南交通大学牵引动力国家重点实验室 成都 610031
0 引言
地铁限界的计算方法经历了不断细化的发展过程。UIC505计算方法以系列标准的形式对车辆提出限界校核方法,但由于UIC标准提供的参考轮廓只适用于欧洲联运铁路,对于不是按照UIC标准修建的线路动态偏移量的设置方法是不同的,所以不能照搬其算法[1,2]。CJJ96—2003《地铁限界标准》计算方法虽然考虑的因素较全面,但因无法准确考虑车辆一系二系振动变形量,且没有车速与悬挂变形的对应关系,所以在确定计算参数时取值均趋向极限状态可能会使计算结果偏于保守[3]。动力学计算方法没有考虑到制造、安装、维护误差等因素,使得计算结果不完全切合实际[4,5]。在总结国内外限界计算方法研究基础和经验的基础上,本文研究出一种基于Matlab编程与三维空间几何变换理论[6]来获取车辆动态包络线的新方法,以某地铁车辆为例,采用线路实测数据获取车辆运行过程中的动态偏移量,再叠加CJJ96-2003《地铁限界标准》[7]计算方法得到车辆的静态偏移量,基于三维空间几何变换理论推导方程,利用Matlab软件编程来计算地铁车辆在实际线路上运行的整个过程中车辆的动态轮廓,得到所有动态轮廓上控制点的坐标,并直接输出车辆的动态包络线,最终实现车辆动态包络线的获取。为了简化计算,本文暂不考虑点头、摇头以及纵向位移对车辆动态轮廓的影响。
1 基于三维空间几何变换的计算方程推导
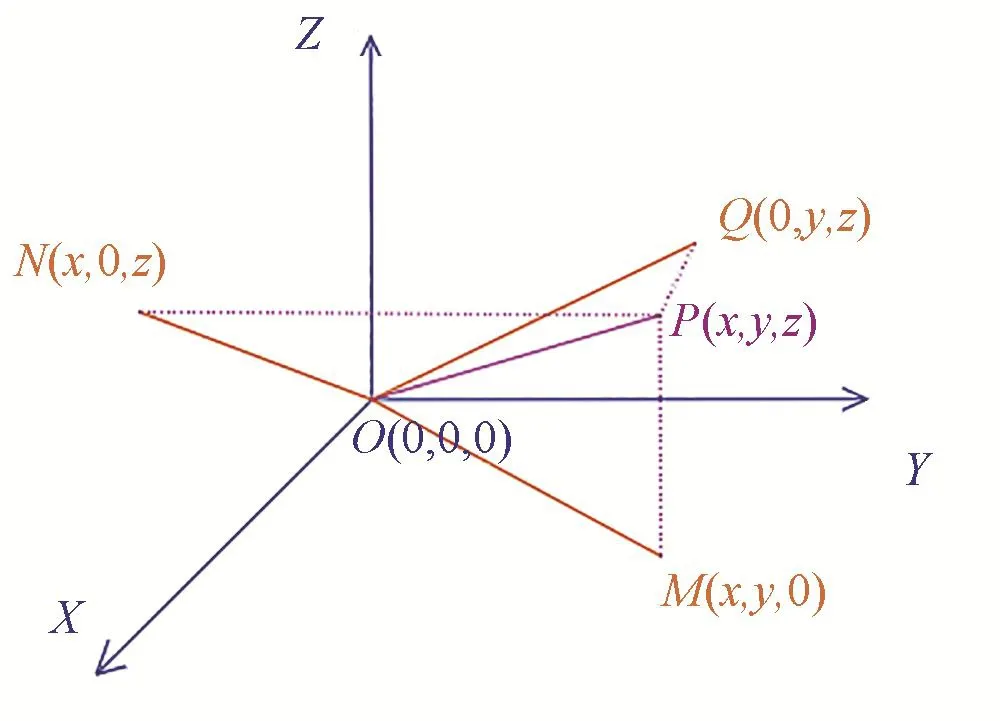
图1 位置示意图
1.1 绕X轴旋转变换

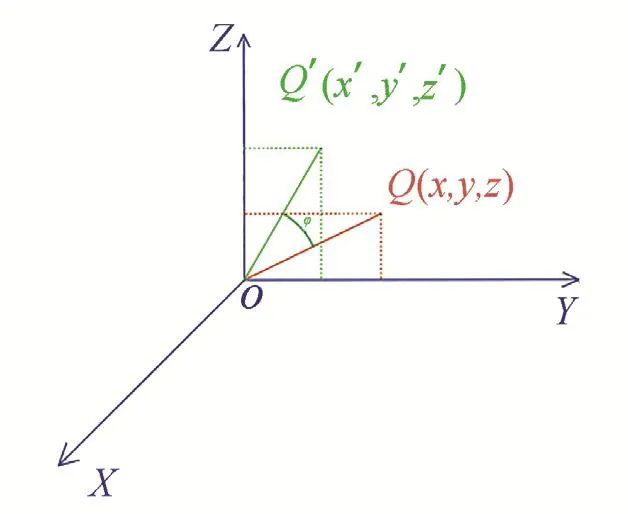
图2 变化前后示意图

1.2 三维平移变换
当空间向量发生平动时可以分解为在三个坐标轴方向的平动,假设在X、Y、Z方向平动值分别为TX、TY、TZ,则发生平动后其坐标只在每个方向的坐标值上分别叠加该方向的平动量。
1.3 三维空间几何变换
当空间向量在三维空间内既平动又转动时,假设先绕X轴转动为再平动为其中转角为φ,在X、Y、Z方向的平动量分别为。则变动前后的坐标关系为

且将矩阵称为三维变换矩阵。
类似的在三维空间中存在某一刚体,其上有任意一点P= (x,y,z),当刚体绕X轴旋转φ角且发生平动后,该刚体上的P点变为P''点,两点之间的关系也可以用上述公式表示。
2 计算截面与控制点
2.1 基准坐标系
轨道坐标的XOY平面位于轨面上,X轴在轨道中心线上并与车辆行进方向一致,Y轴与前者垂直并切于设计轨顶面,Z轴竖直向上,以X轴上任意一点为原点,构建笛卡尔右手直角坐标系O-XYZ[8]。
2.2 计算截面与车辆轮廓线坐标
为了描述整节车辆在线路上的运行行为,一般需在车辆上选择多个截面轮廓来代表整个车辆,称此截面为计算截面[9]。在计算车辆动态包络线时,要先确定车辆的计算截面,车辆的计算截面应建立在车辆运动时车辆轮廓点发生最大位移的截面上,能体现出车辆的最大横向、垂向动态偏移。
现选取车辆的4个计算截面,如图3所示,分别为截面A-A(车体的端部截面)、截面B-B(过前转向架中心的截面)、截面C-C(过车体中心的横截面)以及截面D-D(过后转向架中心的截面)。本文以某地铁车辆为例按上述方法选取计算截面,考虑到篇幅,仅列出A-A断面和B-B断面上控制点坐标,如表1、表2所示。
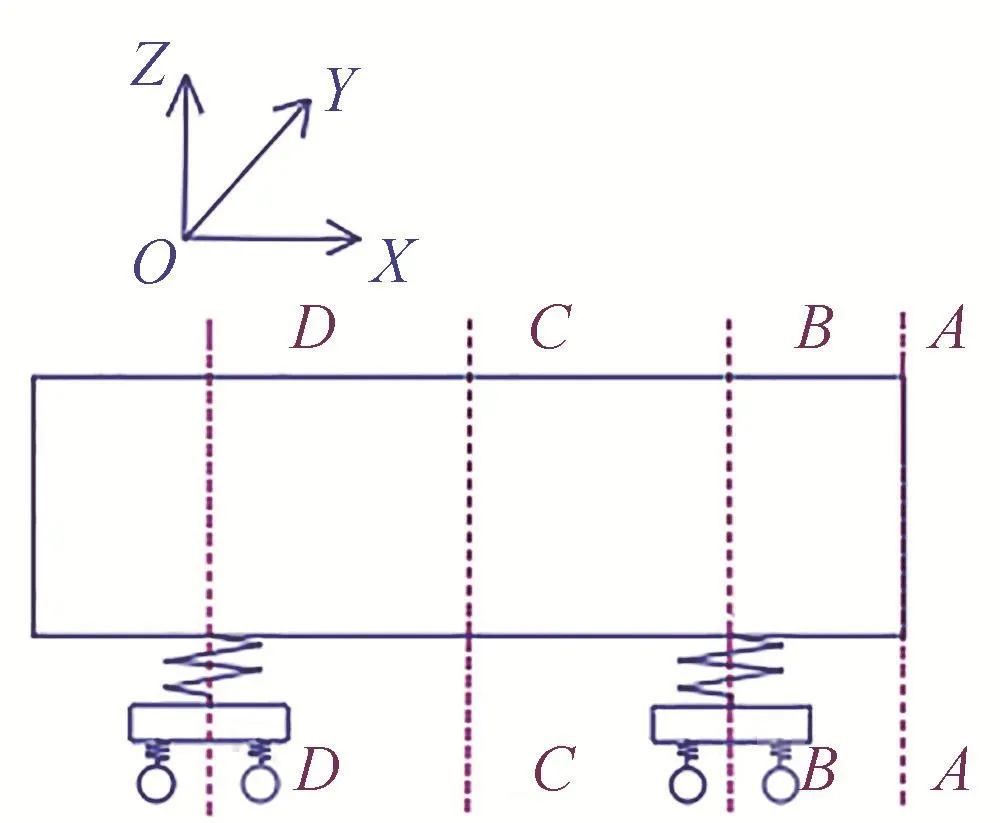
图3 截面位置示意图
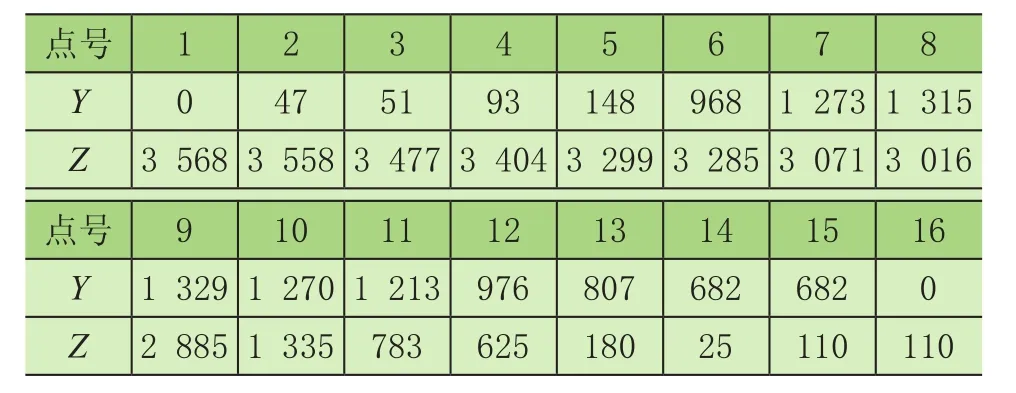
表1 静止状态下车辆A-A轮廓线控制点的坐标 mm
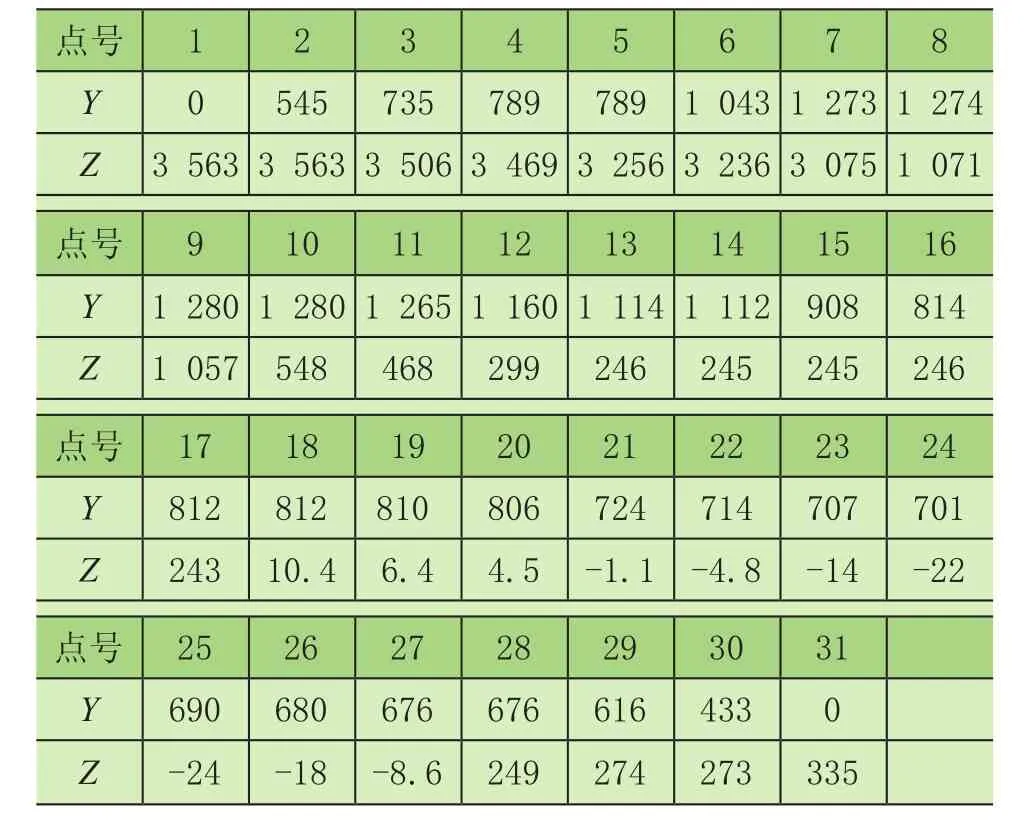
表2 静止状态下车辆B-B轮廓线控制点的坐标 mm
3 动态包络线的获取方法
3.1 获取流程
本文以某地铁车辆为例,研究获取车辆的动态包络线的新方法,获取方法流程如图4所示,通过线路实测数据获取车辆运行过程中的动态偏移量再叠加由CJJ96-2003《地铁限界标准》中的计算方法得到车辆的静态偏移,基于三维空间几何变换理论推导出方程,确定方程中的参数,利用Matlab软件编写函数来计算地铁车辆在实际线路上运行的整个过程中车辆的动态轮廓及其上控制点的坐标,最后通过Matlab编写程序直接输出车辆的动态包络线,最终实现车辆动态包络线的获取。

图4 获取方法流程图
本文在研究车辆的动态包络线问题时,先将计算截面简化,如图5所示。假设车体是绝对的刚体且质量分布均匀,采用前文所述的坐标系O-XYZ,要研究的问题可描述为已知刚性车体平衡状态下的各点的坐标,车辆在线路上运行时产生振动,假设侧滚角为φ,车辆发生的总的垂向偏移量为TZ,总的横向偏移量为TY,总的纵向偏移量为TZ,车辆上存在一点Q,经车辆振动后Q(x,y,z)点最终变为点,两者之间的关系可以用式(4)来表示。

图5 计算截面简图
3.2 三维变换矩阵的参数确定
三维变换矩阵中的参数包括车辆在运行过程中的侧滚角φ以及各方向上的偏移量TX、TY、TZ,本文暂不考虑车辆纵向位移带来的影响所以TX的取值为零。
1)总的垂向偏移量TZ
假设计算截面A-A,B-B,N-N(任意截面)内由一系二系引起的车体的垂向偏移量分别为ZA、ZB、ZN,磨耗引起的垂向固定偏移量及各种安装误差等引起的垂向偏移量为Z、zi,其数值大小可参考CJJ96—2003《地铁限界标准》得到。已知各轮对左侧一系横向坐标yaycyeyg大小为-965 mm,右侧一系横向坐标ybydyfyh大小为965 mm,前后转向架左侧二系横向坐标ypyq大小为-925 mm,前后转向架右侧二系横向坐标ymyn大小为925 mm,且已测得各轮对左右两侧一系引起的垂向偏移量za、zb、zc、zd、ze、zf、zg、zh,前后转向架左右两侧二系引起的垂向偏移量zm、zn、zp、zq。经分析可得在任意截面N-N内,总的垂向偏移量为[4,10]

截面B-B内,由一系二系引起的车体的垂向偏移量zB,可分为两部分,一是由一系引起的车体的垂向偏移量用zB1来表示,二是由二系引起的车体的垂向偏移量用zB2来表示,则有

分别求解zB1和zB2,因为车体是刚性的,所以对于截面B-B内任意点由一系、二系引起的车体的垂向偏移量zB1、zB2而言,其值与在一系、二系左右位置测量出的垂向偏移量有关,之间的关系可以近似为线性的
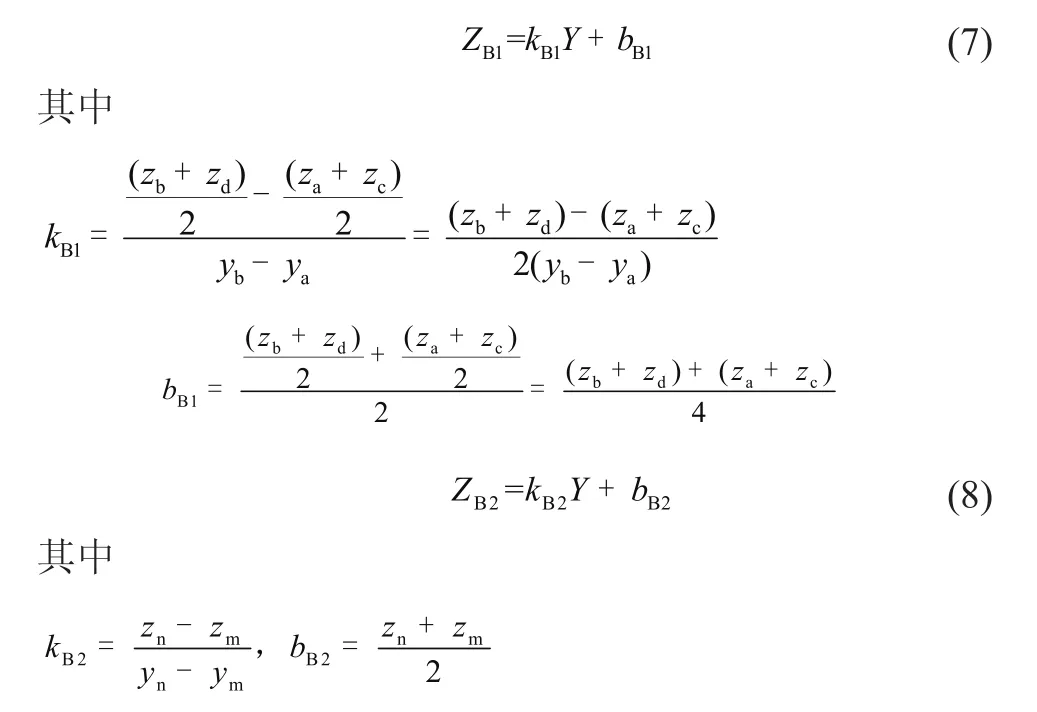
综上可求出截面B-B内,由一系二系引起的车体的垂向偏移量ZB,令ZN=ZB再将其带入式(5)中便得到截面B-B内,车体总的垂向偏移量TZ。用同样的方法可以计算出截面D-D内总的垂向偏移量TZ。
已求出ZB、ZD后可计算除截面B-B、D-D外任意截面N-N内一系二系引起的车辆的垂向偏移量ZN,已知各截面相互平行如图3所示,车辆定距a大小为12 600 mm,以截面C-C所在的位置作为X轴的原点,正方向与车辆行进方向一致,现在引入参数XN,表示任意截面N-N在X轴上的坐标,则有:

令XN=XA,XN=XC代入式(9)即可求得截面A-A,C-C内一系二系引起的车辆的垂向偏移量ZA、ZC。同样在求其他任意计算截面内一系二系引起的车辆的垂向偏移量时,只需要将上式中的参数换成所要计算的截面的X轴坐标即可。综上可求出任意截面N-N内由一系二系引起的车辆的垂向偏移量ZN,再将其代入式(5)中便得到任意截面N-N内总的垂向偏移量TZ。
2)车体总的横向偏移量TY
车辆在线路上运行时,车辆相对于轨道发生的横向偏移量包括:轮对相对于轨道的发生横向偏移Y1,转向架相对于轮对的横向偏移Y2,车体相对于转向架的横向偏移Y3,以及磨耗引起的固定偏移量各种安装误差等引起的偏移量yi。设在任意截面N-N内轮对总的横向偏移量为TY1,转向架总的横向偏移量为TY2,车体总的横向偏移量为TY3,则有[4,10]

根据CJJ96—2003《地铁限界标准》中规定的各个参数的值可以近似求得车辆总的横向偏移量。
3)线路实测数据
运行过程中车体的侧滚角以及由一系二系引起的垂向偏移是随时间变化的。前者是在车体地板中心安装角位移传感器测得的,后者是在一系二系对应位置安装位移传感器测得的。为了使结果更精确更切合实际,在对实测数据进行采样时,将采样频率设置为2 000 Hz,采样时间500 s,最终得到106个采样点,即za、zb、zc、zd、ze、zf、zg、zh、zm、zn、zp、zq,这些参数均取出个数值。由于实测数据较多,此处仅列举抽取的侧滚角φ,以及一位轮对左,一系引起的垂向偏移量za,如图6、图7所示。
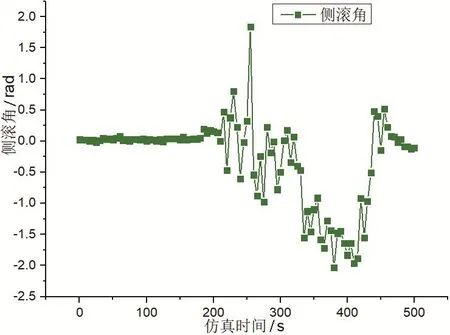
图6 侧滚角φ
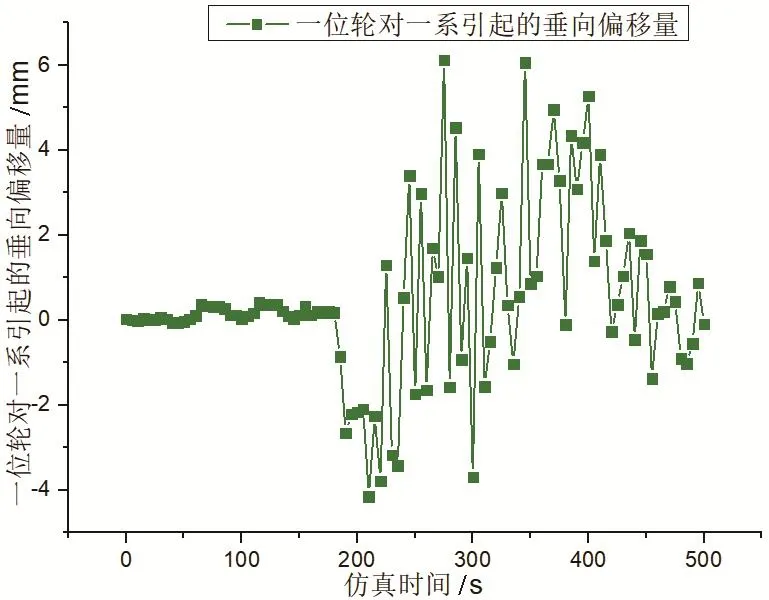
图7 垂向偏移量za
4 基于Matlab获取车辆动态包络线的算例与分析
4.1 车辆动态包络线的获取
在利用推导出的式(4)来计算车辆偏移后各个计算截面内控制点的坐标时,需要很多输入参数,如静止状态下计算截面轮廓线控制点的坐标x、y、z以及TX,TY,TZ,φ (其中x以及TX为零),且本文抽取的线路实际测量的参数均有106个数值,将这些参数带入前文所推导的公式中计算得到ZA、ZB、ZN也均有106个。由于输入和输出的参数数量庞大,本文利用Matlab软件[10]自行编写函数来计算车辆偏移后各个计算截面内控制点的坐标,输出所有偏移的截面轮廓,并通过Matlab中的delaunayTriangulation和convexHull函数来实现车辆动态包络线的获取,计算流程如图8所示。

图8 计算流程图
本文自行编写的函数和脚本主要包括:
1)函数Bver,Dver,Nver,其作用是计算出各计算截面内由一系二系引起的车体的垂向偏移量;
2)函数Balt,Dalt,Nalt,其作用是计算出各截面发生偏移后各控制点的坐标;
3)Bplot,Dplot,Nplot,其作用是输出各截面各个动态偏移轮廓;
4)Bmax,Dmax,Nmax,其作用是得到各截面各个控制点的极限坐标及最大的偏移轮廓,最终得到车辆的动态包络线。
通过Matlab中的delaunayTriangulation和convexHull函数,绘制出这些离散点的最大轮廓,从而实现车辆动态包络线的输出[11]。此处仅列出程序中的部分代码,具体内容如下所示:
DT=delaunayTriangulation(y,z);
%此函数基于列向量y和z中的点创建二维Delaunay三角剖分(y、z为控制点的坐标)
k=convexHull(DT);
%此函数找到返回三角剖分的凸包的顶点
maxY=DT.Points(k,1);
%各截面各个控制点的横向的极限坐标
maxZ=DT.Points(k,2);
%各截面各个控制点的垂向的极限坐标
plot(maxY,maxZ,‘r-’,‘LineWidth’,2);
%画出某计算截面的最大的偏移轮廓,即是所求的某计算截面内车辆动态包络线
4.2 结果及分析
现将已得到车辆在某线路上运行的动态包络线与CJJ96—2003《地铁限界标准》中规定的限界进行对比校核。查找到A1型地铁车辆在高架线曲线段设备限界坐标值输入到Matlab中,最终得到利用本文所提出的方法获取到的车辆动态包络线与标准中的规定的车辆限界之间的关系,此处仅列举计算截面A-A、B-B与标准对比的结果,如图9、图10所示。
图9、图10中黑色的线是车体静态的截面轮廓,黑色的点是控制点的位置,绿色的线是计算截面各个偏移的轮廓,品红色的线是利用本文所提出的方法获取到的车辆动态包络线,蓝色的线是根据CJJ96—2003《地铁限界标准》得到的车辆限界。从图中可以看出本文所获取到的车辆的动态包络线远小于标准中规定的车辆限界,即车辆满足限界要求,可在线路上安全运行。

图9 计算截面A-A的计算结果与对比图
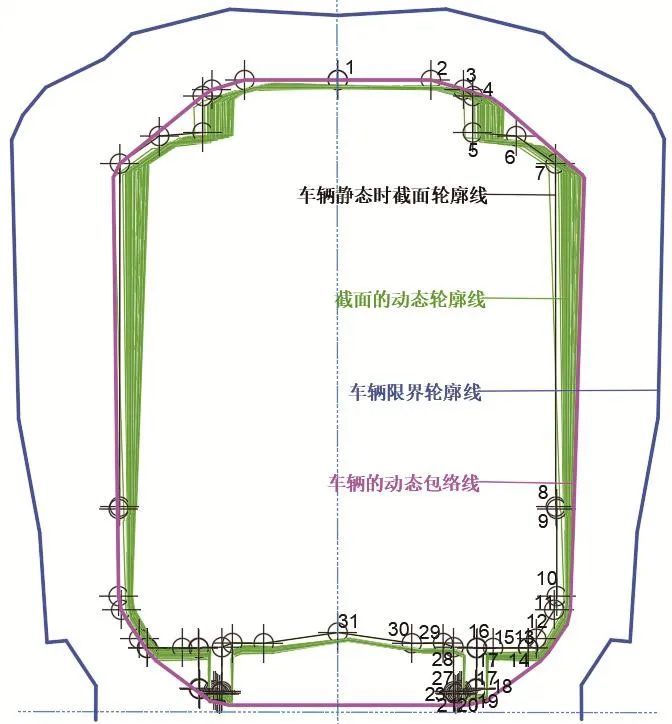
图10 计算截面B-B的计算结果与对比图
5 结论
本文基于三维空间几何变换理论,采用线路实测数据并叠加静态偏移量,利用Matlab软件计算地铁车辆在实际线路上运行的地铁车辆动态轮廓,得到所有动态轮廓上控制点的坐标,并输出车辆的动态包络线,将其与CJJ96—2003《地铁限界标准》中规定的限界进行对比分析,得到如下结论:
1)本文所提出的车辆动态包络线获取方法简单便捷,可操作,易实现,采用线路实测数据并叠加静态偏移使得最终结果更切合实际,可以更加有效地利用限界的有效空间,也为以后的车辆限界计算提供新思路。
2)利用Matlab自行编写函数,能够快速处理大量的数据,使得车辆动态包络线获取更迅速更便捷;通过编写程序可直接输出车辆动态包络线,无需采用CAD绘制最大轮廓图。
3)将本文所获取的车辆动态包络线与CJJ96—2003《地铁限界标准》规定的限界进行对比分析,可知前者远小于后者,即车辆满足限界要求。
