基于信号距离的煤矿电网故障区段定位

2021-03-26冯泽镡赵建文李升健

煤炭工程 2021年3期

杨勇，冯泽镡，赵建文，李升健

(1.西安科技大学电气与控制工程学院，陕西西安 710054；2.国网江西省电力科学研究院，江西南昌 330096)

我国煤矿高压电网的电压等级大多为10kV或6kV。根据《煤矿安全规程》的规定，井下接地电流必须限制在20A以下，越来越多的煤矿高压电网开始采取经消弧线圈接地的运行方式，对系统的单相接地故障电流进行限制。

现有的故障定位方法多基于零序网络对故障信号进行辨识，文献[1，2]提出利用故障后上下游稳态零序电流的幅值极性差异，定位故障区段。但消弧线圈的补偿，使该方法不再适用。文献[3]利用罗氏线圈放大零序谐波信号，并结合矩阵算法实现对煤矿高压电网的故障区段定位，但故障矩阵的构建依赖于检测点上传的信息，存在抗干扰能力差的问题。文献[4]通过GHM多小波变换对故障电流处理，改进了传统小波变换存在奇异点偏移的问题，从而提高故障定位精度，但受矿井下的大量干扰源的影响。文献[5]通过注入原始脉冲实现矿用电缆的准确定位，但相对应的信号检测设备的安装，使得成本有所提高。因此，对于工况环境复杂，干扰源众多的煤矿电网，上述定位方法均存在一定局限性。

本文通过对发生单相接地故障时暂态正序实部电流特征的分析，利用信号距离算法对故障上下游波形的相似度进行衡量，判别出故障区段。并通过不同故障条件下的仿真，验证了本方法不受消弧线圈的影响，在不同故障条件下均能识别故障区段。

1 基于正序实部网络的单相接地故障特性分析

以具有n条馈出线路的经消弧线圈接地的煤矿电网为例，通过瞬时对称分量法对发生单相接地故障的煤矿电网系统进行解耦得到瞬时正序实部网络[6-8]，如图1所示。

图1 单相接地故障的瞬时正序实部网络

在图1的线路l1共设有M、N、P、Q四个监测点，设故障发生在检测点N、P之间。故障点上游监测点M、N的暂态正序实部电流满足：

故障点下游监测点P、Q之间的正序实部电流满足：

对于故障点上下游而言，流过故障上游的电流主要由故障点处的虚拟故障电源提供，以及故障点上游的线路对地电容电流组成；故障点下游为线路对地电容电流。则对于监测点N、P而言，存在以下关系：

各检测点暂态正序实部电流波形如图2所示，具有3条馈出线路的系统发生单相接地故障条件下，故障线路l1各检测点暂态正序实部电流波形(故障发生在NP之间，从上往下依次为上游监测点M、N和下游监测点P、Q波形)，由图2可知故障特征与理论分析一致。

图2 各检测点暂态正序实部电流波形

从图2可以明显看出：故障线路上，故障点同侧的暂态正序实部电流波形相似，而故障点异侧的正序实部电流波形具有差异性。并且，由于正序电流不经消弧线圈，故障特征不受消弧线圈的影响。

2 基于信号距离的故障区段定位

对于波形形状复杂，不甚规整的暂态过渡阶段而言，其分析和处理完全不同于常见的波形规整的正弦信号，无法直接对其幅值、相位、频率等信号特征比较分析；并且由于暂态过程过于短暂，因此对辨识算法的快速性提出了严格的要求。

2.1 信号距离原理

信号距离算法是以加减法运算为主要形式的信号分析方法，具有简单快速的特点。通过计算两个信号在对应时刻的差值，并取其绝对值的区间平均值，来表示两个信号之间的相似程度。

设离散样本信号x(n)和y(n)来自各态遍历平稳随机过程，时限历程为[0，N]，并假定信号是因果的，则两信号的互距离定义如下：

式中，Δxy表示两无时移离散信号之间的距离值。特别，当y(n)≠x(n)时，Δxy表示两信号间的互距离；而当y(n)=x(n)时，称Δxy为信号自距离，自距离值恒为零。因此，对于不同信号之间的差异程度的大小，可以根据它们之间的互距离值大小来表征。信号的相似度越低对应的距离值越大，反之越小。

采用信号距离对信号进行分析处理，不仅能够综合反应信号中每一频率分量的相位关系及幅值信息，弥补了依靠单一频段信息判断故障的信息的不全面性；同时由于算法本身原理简单，不涉及复杂的频率转换，算法的运算速度得到了有效保障。

2.2 基于信号距离的区段定位方法

将故障线路上相邻两个监测点i和j在区间[0，N]的暂态时间内采集到的瞬时正序实部电流带入式(4)，计算得到该区段的信号距离pij，以便于后续对故障路径进行判断及定位故障区段。

针对煤矿电网的多分支结构，分别从以下两种线路结构，给出故障路径的判据及定位故障区段的方法。线路结构如图3所示。

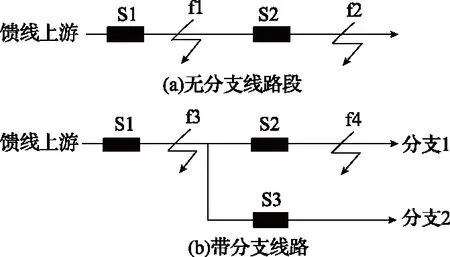
图3 线路结构

2.2.1 无分支线路

对于图3(a)所示的无分支线路，若在f1处发生故障，上游线路长度一般较下游线路大，且上游的电流部分为故障源所提供。因此，流过监测点S1与S2的暂态正序实部电流波形存在差异，得到的信号距离较大。

若在f2处发生故障，流过S1与S2的正序实部电流均属故障上游，均以电容电流为主，因此流过两个开关的暂态正序实部电流，波形相似，信号距离较小。且若馈线上游存在其余监测点，则所有的信号距离值大小较为相近，彼此相差不超过一个数量级。

综上，得到判据1：对于无分支的线路，故障路径直接便可确定，故障路径即为此无分支线路。

2.2.2 带分支线路

煤矿电网线路结构复杂，不乏多分支线路，举图3(b)所示线路进行适当分析。

为便于分析描述，对分支节点处的相邻检测点之间的信号距离进行计算，并将其记为rkl(k，l分别为节点前后相邻的监测点)。

当故障在f3处发生时，流过S1的电流来自故障上游；而流过S2与S3的暂态正序实部电流来自下游支路，得到的r12与r13均较大。由于在这种故障情况下，在故障节点后，选择分支1或分支2对后续故障区段的定位无影响。为简便起见，一般将分支处信号距离较小的分支，作为故障分支。

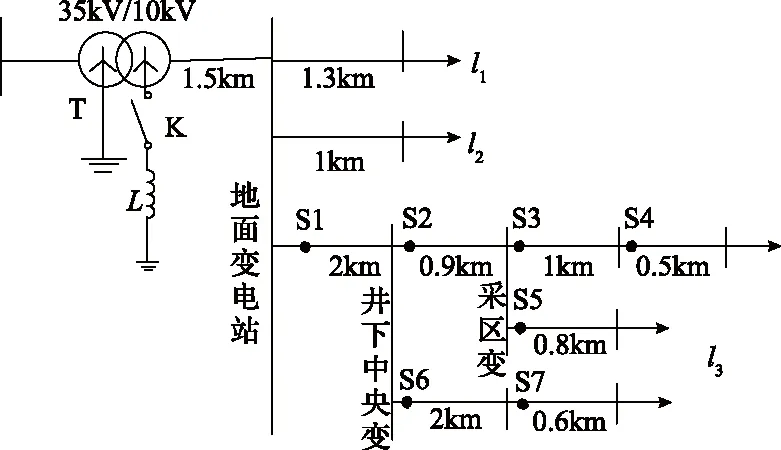
若故障发生在f4处，流过S1与S2的正序实部电流均为上游网络的电容电流，波形相似性大；而流过S3的电流仍为下游支路的电容电流，存在r12

综上，得到判据2：对于带分支线路，若分支节点处相邻检测点暂态正序实部电流互距离值小的分支段，为故障分支。对于有分支节点的线路，重复利用判据2，直到线路末端，得到故障路径。

待故障路径确定后，将故障路径上各区段的信号距离值作为向量P中的元素，形成区段定位向量：

P=[p12，p23，…，p(m-1)m]

(7)

若某一区段发生接地故障，区段定位向量中最大元素pmax=max{pij}对应为故障区段。

2.3 故障区段定位流程

经过大量学者及科研单位的深入研究，故障选线技术现已颇为成熟，并推出了一系列适用于矿井的微机选线装置，故本文的定位方法建立在故障线路已知的情况下，进行基于信号距离的故障区段定位。定位方法的步骤如下所示，其流程如图4所示。

图4 区段定位流程图

1)确定故障线路。首先对是否发生故障进行判别，检测母线上瞬时零序电压，当其超过0.15倍额定电压幅值时，发生单相接地故障。根据集中式区段定位的原理，启动故障选线算法，确定故障线路，并将选线结果上报主站。

2)采集暂态正序实部电流信号。通过故障线路上的各监测点，对故障后1/4工频周期内的三相电流进行采集。采样频率选为10kHz，即每工频周期采样200点。并通过瞬时对称分量法获得相应的瞬时正序实部电流，上传至主站。

3)计算相邻检测点的信号距离值。主站根据传输过来的1/4工频周期正序电流信息计算故障线路上各相邻检测点之间的暂态正序实部电流互距离值。

4)确定故障路径。根据故障线路是否存在分支节点，决定下一步骤的执行。若故障线路无分支，则故障路径即为该故障线路；若存在分支节点，则通过比较分支节点处相邻监测点的区段信号距离值判断故障分支，直到线路末端，确定故障路径。

5)定位故障区段。将故障路径上各区段的信号距离值重构，得到故障区段定位向量P，根据向量中的最大元素pmax=max{pij}定位故障区段。

3 仿真实验

3.1 仿真模型

依据实际煤矿电网结构，通过Matlab/Simulink软件平台对系统进行仿真建模，如图5所示。该仿真系统为典型单源辐射式网络结构，以中性点经消弧线圈接地方式运行，共有3回出线，各检测点编号及馈线区段长度如图5所示。电缆线路采用π形参数模型，其正序参数为R1=0.11Ω/km，L1=0.52mH/km，C1=0.29μF/km；零序参数为R0=0.34Ω/km，L0=1.54mH/km，C0=0.19μF/km。系统以过补偿状态运行，脱谐度v为-10%，零序电感L=1.364H，采样频率为10kHz。

图5 10kV煤矿电网仿真模型

3.2 仿真算例

对图5所示系统，在线路l3的监测点S3-S4之间设置单相接地故障，故障时刻为0.02s，系统以脱谐度v为-10%的过补偿状态运行；漏电电阻Rf取100Ω；漏电角q=90°。故障线路上各监测点的暂态正序实部电流如图6所示。

图6 故障线路各检测点的瞬时正序实部电流

从图6可以明显看出，对于故障点异侧的暂态瞬时正序实部电流波形差异显著；而位于故障点同侧的暂态瞬时正序实部电流波形相似度较高。

分别对故障后1/4周期的相邻监测点之间的正序实部电流进行信号距离计算。由于在分支节点1和分支节点2处存在r12

3.3 方法适应性验证

设定仿真系统在0.02s发生单相接地故障，故障位置设为监测点S3至S4之间，在不同漏电初始角的情况下，漏电电阻为100Ω时，故障路径及区段定位向量的计算结果见表1；通过设定漏电初始角q=60°，分别在不同漏电电阻的条件下，对故障区段进行判定，不同漏电电阻下故障区段定位结果见表2。漏电角设定为90°且漏电电阻定为100Ω的条件下，针对不同的故障位置，对故障定位方法进行了验证，不同故障区间下故障区段定位结果见表3。