一种两自由度飞行机械臂系统的设计与实现

何慰，方勇纯,*，梁潇，张鹏

1. 南开大学 机器人与信息自动化研究所，天津 300350 2. 天津市智能机器人技术重点实验室，天津 300350

旋翼无人机在应用领域受到越来越多的关注。由于其结构简单、成本低廉的优点，被广泛应用于航拍、电力巡检、巡逻等应用领域[1]。在这些应用场景中，无人机主要用于环境感知，缺乏和环境的主动交互。飞行机械臂系统是在旋翼无人机上安装带有末端执行器的机械臂，增强了无人机系统和环境的交互能力，从而使其在货物抓取与运输、装配、样品采集、救灾等领域发挥极大的作用[2-7]。

旋翼无人机本身存在欠驱动性和状态变量之间的耦合特性[8]，在增加机械臂后不仅增加了系统的耦合性，还增加了系统自由度数量，使得系统模型极为复杂。在考虑无人机自身受到干扰的情况下，需要7自由度机械臂才能使得末端执行器以任意姿态到达工作空间内任意工作点且抑制扰动的影响[5]。因此飞行机械臂系统一般为高冗余系统，这使得该系统的运动规划问题非常困难。无人机带臂飞行过程中，机械臂产生的质心偏移会使无人机受到更大的离心力和科氏力影响；而在机械臂动态运动过程中，也会对无人机产生反作用力，这些扰动会显著影响无人机的稳定性。综上所述，飞行机械臂系统在建模、规划和控制等方面都十分有挑战性。

在建模方面，主要有牛顿-欧拉法和欧拉-拉格朗日法[9]。前者在实际应用中易于实现，后者由于显式地给出系统质量矩阵、广义科氏力矩阵和重力矩阵，便于进行控制器的设计和分析。机械臂对无人机系统的影响既可以被视为扰动[10]，也可以与无人机作为一个整体精确建模[9,11-12]，同时还可以将机械臂的部分影响建模到整体模型中而忽略次要影响[13]。Zhang等[13]将机械臂运动过程中机械臂的质心偏移建模到系统中，在控制器设计中忽略了难以获得和计算的机械臂惯性张量矩阵。文献[14]对飞行机械臂系统的模型在平衡点附近做了局部线性化。在控制器设计方面，处理机械臂对无人机影响的方式有多种：① 将 机械臂及负载的影响当作外部扰动，使用抗扰控制或扰动观测器估计并补偿；② 将机械臂对无人机的影响建模，直接计算出其对无人机的扰动并补偿；③ 将机械臂与无人机进行整体建模和控制。文献[15]对系统进行了整体建模，使用了反馈线性化和一定的模型简化对内外环解耦，并使用自适应控制处理模型误差和外界扰动。Kim等使用了飞行机械臂整体模型，设计了滑模自适应控制器[11]。文献[16]采用了扰动观测器和鲁棒控制来处理机械臂及负载扰动。处理飞行机械臂系统与外界环境之间的交互可以采用阻抗控制的方法[12]。此外，可以综合多种方法抑制机械臂以及外界扰动：对飞行机械臂的部分扰动建模，如质心偏移等，并使用电池的位置进行补偿，然后将其他部分使用扰动观测器来估计并补偿[10]。

本文设计了一种2自由度飞行机械臂系统，对系统整体建立了精确的模型，并在一定条件下对模型进行简化。对简化模型设计了基于内外环的控制器，并通过仿真验证了控制方法的可行性和有效性。本文其余部分组织如下：第1节对设计的飞行机械臂系统进行介绍；第2节介绍系统模型的构建；第3节实现了控制器设计；第4节介绍仿真实验并分析实验结果；第5节是总结和展望。

1 系统设计

本文设计的飞行机械臂系统如图1所示。无人机采用轴距450 mm的四旋翼无人机，搭载Pixhawk开源飞控，使用Raspberry Pi 3作为机载电脑。无人机的动力系使用T-MOTOR MN3508无刷电机、HOBBYWING XRotor Micro 40A BLHeli_32 DShot1200电调。

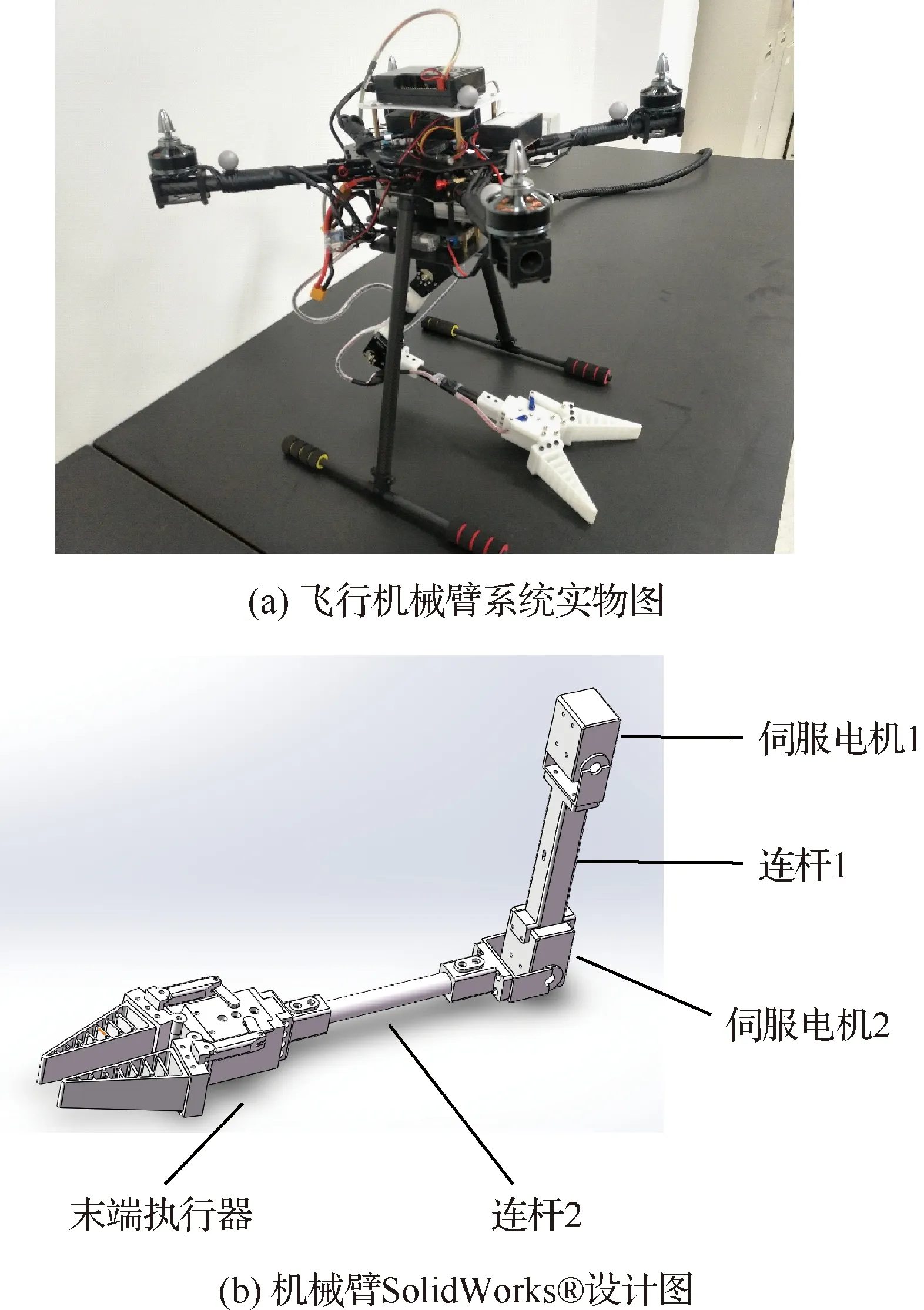
图1 飞行机械臂系统Fig.1 Aerial manipulation system

为了能够实现抓取任务，避免机构过于复杂，确保系统重量适中，采用2自由度机械臂的pitch-pitch配置。使用ROBOTISE公司的Dynamixel XH430-W350R总线舵机直接驱动。机械臂的各个连接部件采用3D打印的方式加工。机械臂的硬件驱动系统如图2所示。

图2 机械臂硬件Fig.2 Hardware of manipulator

为了适应抓取任务，机械臂末端的夹爪应该具有较快的张合速度，因此使用了一种舵机(KST DS145MG)驱动的平行四边形四连杆机构(如图3所示)。由于环境和系统本身的限制，不能保证以最合适的角度接近被抓取物体，并且无人机在飞行和悬停过程中存在抖动，因此采用了基于鳍条效应(Fin ray®effect)的夹爪手指[17]。这种仿生学设计可以自动贴合被抓取物体，对于抓取角度误差和不规则物体有很强的包容性。

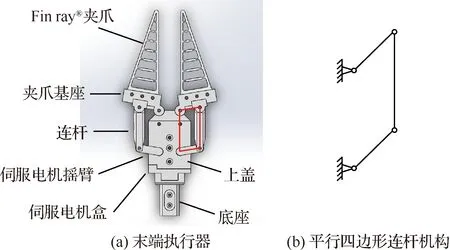
图3 机械臂末端执行器Fig.3 End effector of manipulator

2 系统模型

本节将首先介绍飞行机械臂系统的运动学模型，在此基础上根据欧拉-拉格朗日方程构建系统完整的动力学模型，最后根据特定假设对动力学模型进行简化。

2.1 运动学模型

系统坐标系和动力学参数如图4所示。Σb、ΣC1、ΣC2分别代表位于无人机质心以及2个机械臂连杆质心处的坐标系；O0、O1、O2、Oe为分别固连在无人机、连杆1、连杆2、末端执行器上的坐标系原点[18]。L1、L2分别表示2个机械臂连杆的长度。

图4 飞行机械臂系统示意图Fig.4 Illustration of aerial manipulation system

(1)

记机体坐标系到惯性坐标系的旋转矩阵为Rb，其表达式为

(2)

式中：s和c分别代表正弦和余弦函数。则有

(3)

(4)

式中：[·]×表示对向量取反对称矩阵。将式(4)展开后可得[18]

(5)

(6)

表1 坐标系相互关系Table 1 Relationships between coordinates

机械臂各个连杆的质心(Ci)位置在惯性坐标系下的表示(pCi)为

(7)

经过计算得到连杆1和连杆2的运动学方程为

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

于是可以得到各个连杆相对于惯性坐标系的运动学方程为

(16)

(17)

(18)

2.2 动力学模型

下面使用欧拉-拉格朗日法建立系统完整的动力学模型:

(19)

L=K-U

(20)

(21)

于是有

(22)

无人机旋翼产生的升力大小为F，则有

(23)

(24)

(25)

式中:M11(q)∈R3×3，M22(q)∈R3×3，M33(q)∈R2×2为正定对称矩阵；M12(q)=M21(q)T∈R3×3，M13(q)=M31(q)T∈R3×2，M23(q)=M32(q)T∈R3×2。

(26)

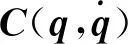
i,j= 1,2,…,8

(27)

G(q)的计算方式为

(28)

2.3 模型简化

将式(24)写成分块矩阵的形式:

(29)

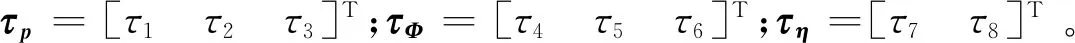
(30)

因而可以得到无人机子系统模型

(31)

3 控制器设计

飞行机械臂系统是一个高度非线性的系统，机械臂的构型和运动增加了整个系统的复杂度，使得对于系统的整体控制非常困难。由于无人机内环动态显著快于外环，因此可以针对无人机内环与外环分别设计控制器。

(32)

(33)

从而可得新的系统为

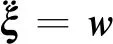
(34)

由式(33)可以看出，在设计外环控制器输入τp时需要使用内环控制器辅助输入w2，然而此时w2是未知的。为了消除设计控制器时内环和外环之间的耦合，可以将M12置为0。记新的质量矩阵为

(35)

文献[20]通过仿真结果指出，由于飞行机械臂系统中机械臂的质量一般显著低于无人机，因此相比于M11，M12可以忽略不计，因而式(35)是合理的。于是新的控制输入为

(36)

由此外环引入了建模误差，将外环的建模误差和空气阻力扰动、负载变化等统一表示成未知扰动d∈R3。最终得到内外环2个子系统

(37)

反馈线性化后的精确模型为

(38)

(39)

3.1 外环滑模控制器

对外环子系统设计滑模控制器[21]。无人机质心的位置期望轨迹为pd，用户给定偏航角为ψr，则外环位置和速度跟踪误差为

(40)

定义滑模面为

(41)

式中：Α=diag(α)，α∈R3，α>0。则可以得到辅助控制输入为

(42)

其中：K=diag(k)，k∈R3且满足：

k≥|d|

(43)

其中：|·|代表对矢量各元素求绝对值。于是可以得到外环的控制输入为

(44)

由此，可以得到期望升力为

(45)

由于升力的输入和无人机姿态耦合，造成了无人机的欠驱动性质。具体而言，无人机升力的方向与机体坐标系z轴平行，因此机体坐标系期望姿态下的z轴单位向量为

(46)

由给定期望偏航角ψr，可以得到期望姿态下机体坐标系x轴单位向量为

(47)

无人机机体坐标系的x轴和z轴不能任意配置，因此只能保证机体坐标系x轴和期望方向在同一垂直平面内[22]，所以期望姿态下的机体坐标系可以定义为

(48)

由此可以得到期望姿态的旋转矩阵为

(49)

进而可以得到期望姿态对应的欧拉角为

(50)

其中:

(51)

式中：Rb,d(i,j)表示矩阵Rb,d第i行第j列的元素。

此外，由于存在sgn(s)这一不连续函数，闭环系统会出现抖振现象。为了消除系统的抖振现象，并且使得内环控制器的期望连续可微，可以使用连续的函数来近似不连续的符号函数，本文使用的近似函数为双曲正切函数tanh(10s)。

3.2 内环控制器

由于内环的期望ψd、θd、φd由外环得到，因此很难解析获得它们的高阶导数，而需要使用数值微分得到。数值微分会严重受到噪声影响，破坏系统的稳定性。根据时标分离原则，考虑内环是一个快变系统，且其暂态过程对外环可以忽略，则可以将内环的跟踪当作一个镇定问题，这样一来，可以认为期望姿态欧拉角的二阶及以上导数为0，由此可以得到误差

(52)

设计PID控制器为

(53)

式中:Kp∈R3×3、Ki∈R3×3、Kd∈R3×3为非负对角增益矩阵。由此可得内环控制输入为

(54)

该控制输入为欧拉角对应的广义力矩，需要转换为施加到系统上的真实力矩。根据式(22)，可以得到机体坐标系下的力矩输入为

(55)

4 仿真实验

本节介绍物理仿真实验结果。通过机器人物理仿真软件v-rep[23]和MATLAB进行仿真，和开源飞控Pixhawk中采用的基于四元数的PID算法进行对比。本文设计了3种仿真实验场景来测试所提方法在机械臂静态和动态扰动环境下的镇定和轨迹跟踪性能。为了解决不连续滑模控制带来的抖振问题，在实现控制器时将符号函数sgn(s)替换为双曲正切函数tanh(10s)。

实验1机械臂静态偏置下的镇定实验。设置机械臂静态偏置为η1=60°,η2=30°。由于机械臂的偏置，系统的质心偏离机体坐标系原点。实验结果如图5所示。

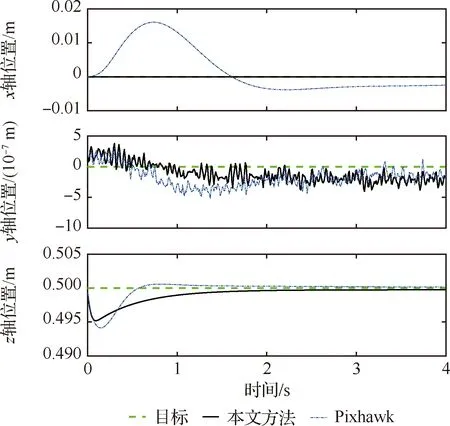
图5 实验1无人机位置Fig.5 Positions of UAV in experiment 1

实验2机械臂周期性摆动下的镇定实验。机械臂在2个关节位形之间(η1=60°,η2=30°和η1=-60°,η2=-30°)做周期性摆动。实验结果如图6～图8所示。

图6 实验2无人机位置Fig.6 Positions of UAV in experiment 2

图7 实验2无人机姿态(Pixhawk方法结果)Fig.7 Orientations of UAV in experiment 2 (results of Pixhawk method)

图8 实验2无人机姿态(本文方法结果)Fig.8 Orientations of UAV in experiment 2 (results of presented method)

实验3机械臂周期性摆动下的直线轨迹跟踪实验。机械臂在2个关节位形之间(η1=60°,η2= 30°和η1=-60°,η2=-30°)做周期性摆动，同时无人机跟踪三次样条速度曲线。实验结果如图9～图11所示。

图9 实验3无人机位置Fig.9 Positions of UAV in experiment 3

图10 实验3无人机姿态(Pixhawk方法结果)Fig.10 Orientations of UAV in experiment 3 (results of Pixhawk method)

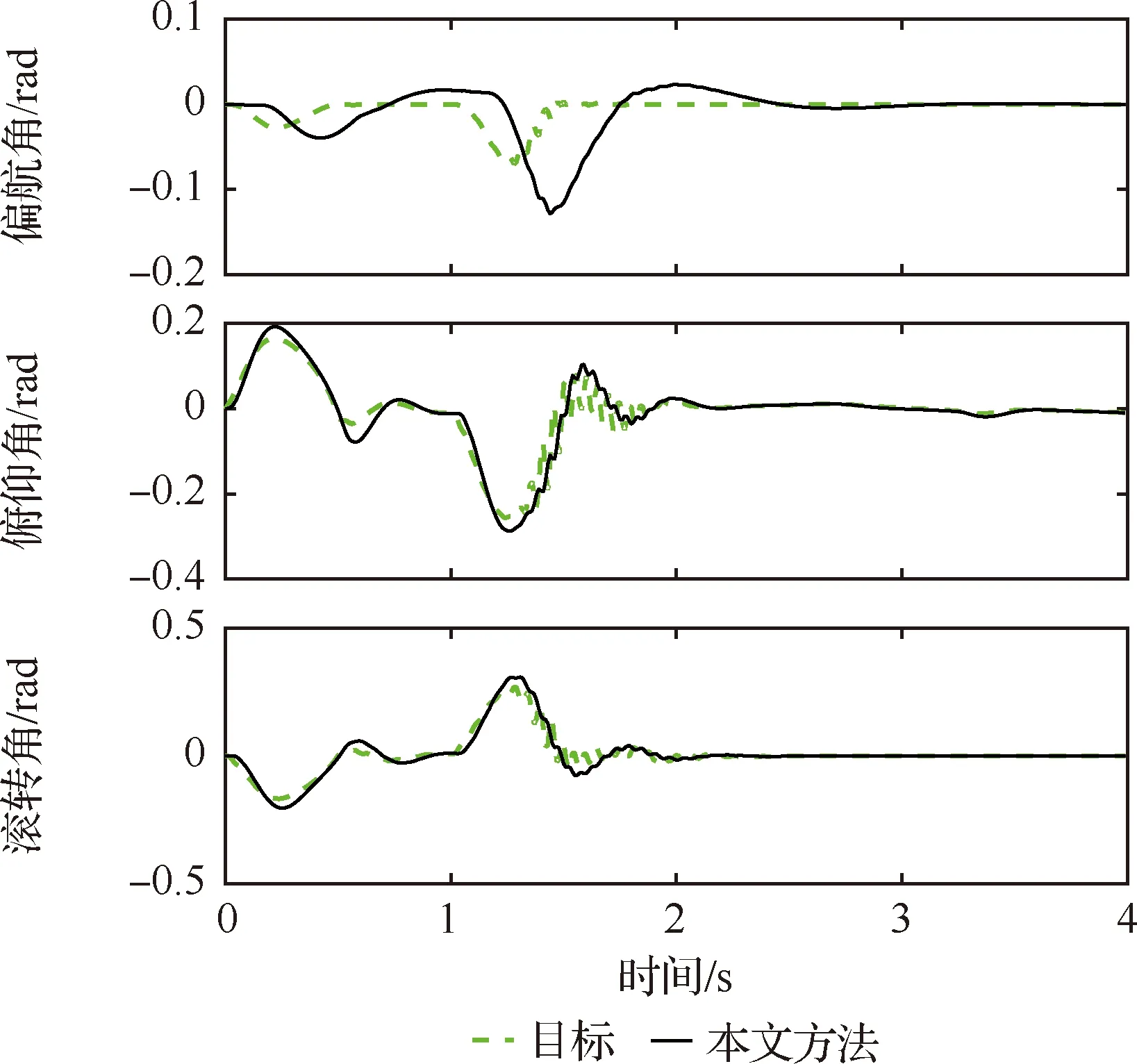
图11 实验3无人机姿态(本文方法结果)Fig.11 Orientations of UAV in experiment 3 (results of presented method)

实验4机械臂周期性摆动下的S形曲线轨迹跟踪实验。机械臂在2个关节位形之间(η1=60°,η2=30°和η1=-60°,η2=-30°)做周期性摆动，同时无人机跟踪S形曲线。实验结果如图12～图15所示。

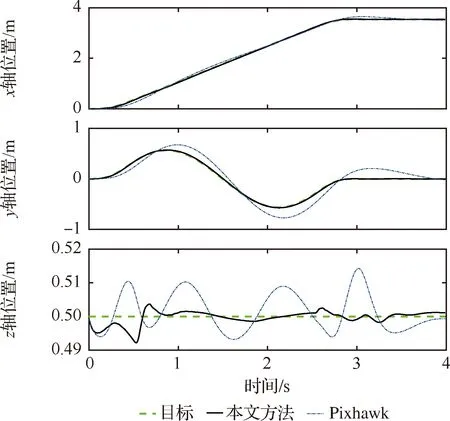
图12 实验4无人机位置Fig.12 Positions of UAV in experiment 4

图13 实验4无人机位置误差Fig.13 Position errors of UAV in experiment 4

图14 实验4无人机姿态(Pixhawk方法结果)Fig.14 Orientations of UAV in experiment 4 (results of Pixhawk method)

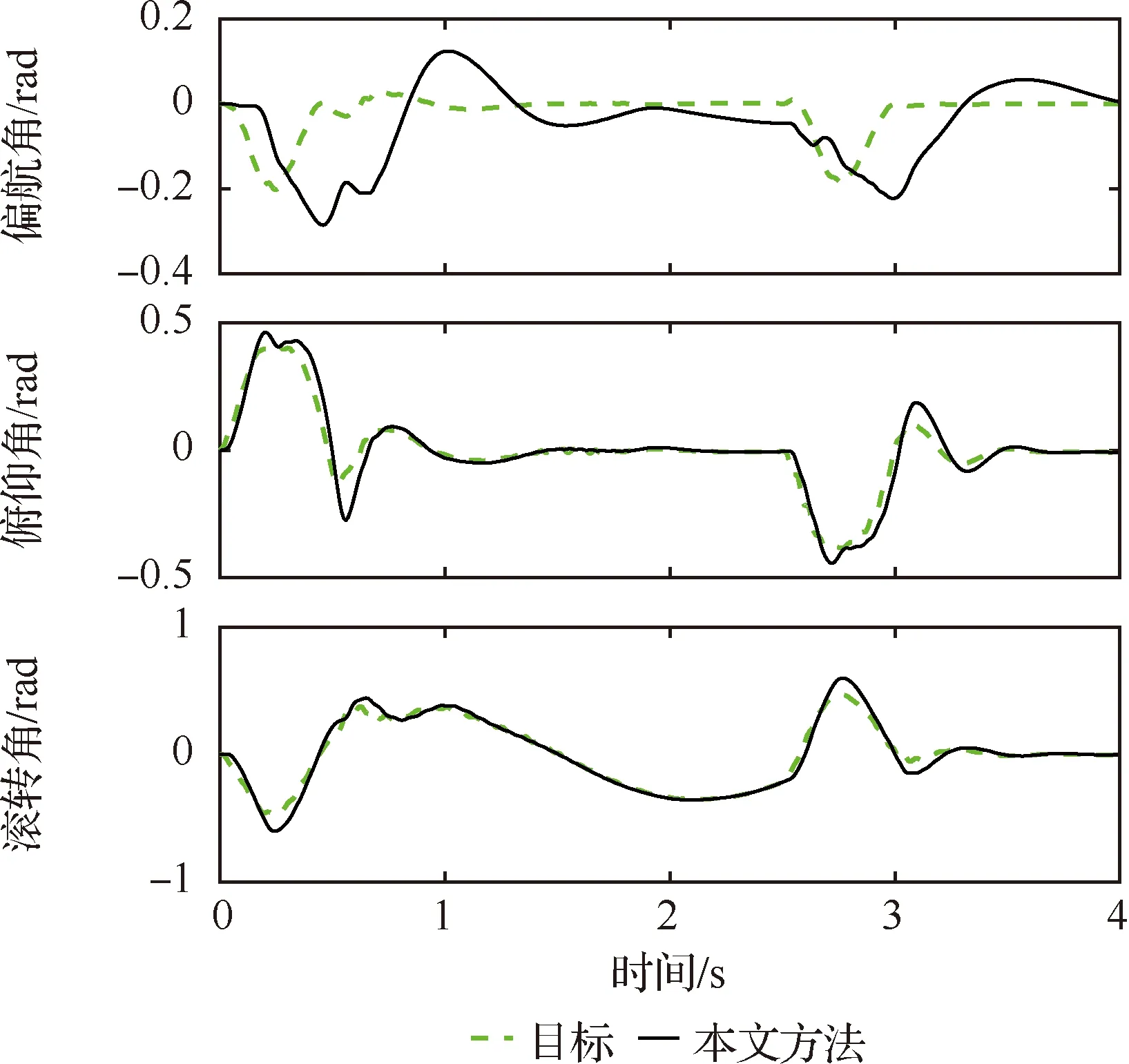
图15 实验4无人机姿态(本文方法结果)Fig.15 Orientations of UAV in experiment 4 (results of presented method)

由图5可以看出，相比于Pixhawk采用的基于四元数的串级PID算法，由于对机械臂质心偏移进行了补偿，所提方法在3个坐标轴方向上位置误差均有明显改善。通过对图6、图9、图12、图13分析可知，存在机械臂摆动时，所提方法的无人机位置误差均低于Pixhawk的算法。通过对图7、图8、图10、图11、图14、图15的对比可以观察到，在所有实验中，所提方法的姿态误差均小于Pixhawk的算法。因此所提控制方法能够明显抑制机械臂静态偏置以及动态摆动对镇定及跟踪性能的影响，其位置误差和超调以及姿态误差均明显低于Pixhawk基于四元数的串级PID算法。实验证明了所提控制方法对于飞行机械臂系统的有效性。

5 结 论

本文设计了一种2自由度飞行机械臂系统，并搭建了飞行机械臂实物平台。使用欧拉-拉格朗日法建立了系统模型。针对机械臂缓慢运动的情况，对系统模型进行了有效简化，降低模型的复杂度，基于此设计了内外环分离的控制器。仿真实验证明了所提方法对于带有机械臂扰动的无人机镇定和轨迹跟踪任务均具有较好效果。在接下来的工作中，将会考虑使用范围更广的模型假设。由于欧拉角的奇异性和不连续性问题，还将考虑内环使用基于旋转矩阵或者四元数的姿态控制方案。

[21] KHALIL H K. Nonlinear systems[M]. Upper Saddle River: Prentice Hall, 2002: 552-579.