日地L2点航天器编队的分布式自主相对导航

叶子鹏，周庆瑞，王辉

中国空间技术研究院 钱学森空间技术实验室，北京 100094

日地L2点位于日地动力学平衡点，是进行天文观测与研究的理想位置[1-2]。在日地L2点部署探测器编队可实现高精度的光干涉测量，是深空探测的重要手段，如美国的TPF计划[3-4]。L2点的深空探测编队对相对控制和导航精度提出了很高要求。

对于地球轨道航天器编队的相对导航，采用全球导航卫星系统(Global Navigation Satellite System，GNSS)与惯性导航系统(Inertial Navigation System，INS)结合的导航方法通常是最便捷有效的[5-7]，但并不适用于深空探测任务，一种工程可行的方法是通过测量航天器间的距离与方向信息，估计出航天器的相对状态信息。Kim[8]与Alonso[9]等研究了基于视线矢量量测的航天器编队相对导航，但是对视线矢量的量测需要光学传感器，在有限的星载资源下，所能量测的视线矢量数量有限，量测过程也较为复杂。Kuang等[10-11]提出了一种通过测距进行航天器编队相对导航的方法，该方法在工程上更可行，但未深入研究影响滤波精度的要素。Mcloughlin等[12-13]在滤波算法上进行了改进，首先利用自主编队飞行(Autonomous Formation Flyer, AFF)传感器测量航天器间的相对距离与方位，再结合改进的加权最小二乘法，对航天器间的相对状态进行估计，同时对有限资源下AFF传感器的调度问题进行了研究。Wang等[14-16]对分布式定位算法进行了研究，其算法可以实现高精度定位。他们基于对LEO轨道航天器的定位结果，实现了航天器高精度的协同控制。Ferguson和How[17]等针对编队飞行相对导航中计算量较大的问题进行了研究。采用了Schmidt-Kalman滤波方法，通过降低所需估计的状态维度，从而减少了计算量。但是随着编队成员数量增加，不同航天器之间的协方差矩阵处理会变得复杂。同时，该算法需要提前设置编队中航天器的滤波顺序，并且所有航天器需要按顺序进行信息交互，因此本质上该算法是集中式的。

本文研究了日地L2点的探测器编队仅通过星间测距进行相对导航的方法。由于实际工程中航天器的惯性姿态易于获取，比如采用小型化的星敏感器即可获得很高精度的惯性姿态，因此假设各航天器三轴惯性姿态已知，在此情况下研究相对导航问题，更具有实际价值。

为了避免集中滤波计算量过大，同时考虑在深空环境中保证较高滤波精度，本文提出了一种分布式的相对导航方法。并对影响导航精度的要素进行了分析，对某些可解耦项进行了精确地拟合，研究结果对实际工程具有一定参考价值。

1 分布式自主导航方法

基于AFF的方法可以实现一对地球轨道主从星之间可靠的相对导航。即使量测量较少，量测精度较低，滤波结果也能够收敛。这是由于滤波结果受到非线性的地球轨道相对运动方程的约束，其运动轨迹不仅要符合量测值，同时也要符合相对运动方程的解。这样的强约束导致滤波结果容易收敛。日地L2点主从星之间的相对运动方程是线性的，对滤波结果约束较弱，仅通过某一从星与主星之间测距进行相对导航的方法容易导致滤波误差发散，尤其当从星与主星距离较远时，可能会产生多组同时符合量测值与相对运动方程解的结果。

传统的去中心化方法结合所有从星的相对运动方程，每个从星都对全局状态信息进行估计，能够有效解决滤波误差容易发散的问题。但是在传统的去中心化方法中，当编队规模较大时，全局状态维度过高，每一次估计的计算量较大，因此，本文提出了一种仅采用局部测量信息的分布式导航方法，不仅具有较低的状态估计维度，同时可通过数据融合保持较高的估计精度。

不失一般性，以一个4星编队为例介绍提出的分布式自主导航方法。在编队中两两之间存在测量关系，其示意图如图1(a)所示。

本文主要研究航天器编队的相对导航问题，假设主星(Chief)的状态信息已知。在此假设下，如果采用集中式方法，每颗星都要进行18维全局状态估计，且随着编队成员的增加，待估计状态数线性增加。针对此问题，提出了一种采用局部测量信息的导航方法，如图1(b)～图1(d)所示，每颗从星选择主星和另一颗从星组成三角量测构型，量测值为3颗星相互的测距值。由于主星的状态信息可视为已知量，故每次只需估计2颗从星的状态信息。在此模型中，每颗从星的状态信息都可能被估计多次，可采用信息融合方法获取最终状态信息。

在实际场景中，当存在更多的从星时，可采用如下策略进行量测构型生成：每个从星与自己最近的从星，以及主星生成三角量测构型。如果2颗从星互相选择，则其中一颗选择其他从星生成量测构型。如从星i与从星j互为最近邻星，当i选择了j后，从星j则不能选择i，只能选择离自己次近的从星k。以上策略可以保证所有航天器都至少有一次状态估计。当完成滤波后，每个从星收集关于自身的状态估计信息，如果信息组数大于等于2组，则对多组信息进行融合，从而完成对自身状态的估计；如果某航天器收集的关于自身的信息组数小于2组，则该航天器在自身未选择的航天器中再选一颗最近的，生成量测构型，对自身再进行一次状态估计，从而得到2组估计值，进行信息融合。

本文的算法可总结如下：

图1 编队量测构型示意图Fig.1 Diagram of formation measurement configuration

步骤1通过通信协商形成三角测量划分，原则是各个航天器不选择重复的三角形。

步骤2根据测量构型，分别进行测量和状态估计。

步骤3对多组估计数据融合，得到最终结果。

步骤4与邻居的拓扑关系是否改变，如改变转到步骤 1，如未改变转到步骤 2。

以图1所示的构型为例，提出的航天器编队分布式自主导航的全部过程如图2所示。每颗从星都得到了多组状态估计，通过信息融合，可以得到每颗从星较高精度的状态估计。

图2 编队状态估计流程图Fig.2 Flow of formation state estimation

2 相对导航的数学模型

地球轨道航天器编队通常采用CW方程[8,18]作为相对运动方程。但是日地L2点附近的Halo轨道属于三体轨道[19]，CW方程不适用。由于L2点的重力梯度较小，可假设航天器编队间的相对运动不受约束，只受牛顿第二定律的作用。

2.1 相对运动方程

令从星i相对于主星的状态信息为

i=1,2,3

(1)

令间隔时间为ΔT，受牛顿第二定律作用，短时相对匀速运动可描述为

Xi(k+1)=ΦXi(k)+ΓWi(k),i=1,2,3

(2)

式中：Wi(k)为噪声；Φ与Γ为状态转移矩阵，可以表示为

(3)

(4)

其中：I3×3为三阶单位阵。令本体坐标系下从星i的转动速率为ωi，主星的转动速率为ωc，则从星i相对于主星有

(5)

Mi=Rz(ψi)Ry(θi)Rx(φi)

(6)

根据式(5)和式(6)可以得到从星i相对于主星的欧拉角速率为

(7)

式中：f(φi,θi,ψi)是与从星i相对于主星本体坐标系的欧拉角相关的矩阵，可由式(5)求得。

2.2 量测模型

量测模型的示意图如图3所示，每2颗航天器之间通过收发天线进行测距，结合天线的本体系安装位置，可以建立量测方程。图中：Rcd为惯性系下从星Deputy 1相对于主星的位置；Rct为主星本体系下发射天线的安装位置；Rdr为从星Deputy 1本体系下某一接收天线的安装位置；Rct与Rdr均为已知量；Rtr为从星接收天线与主星发射天线在主星本体坐标系下的距离矢量。

量测量为发射天线与接收天线之间的距离，可以得到量测量为

(8)

式中：Mci为主星相对于惯性系的姿态矩阵；Mcd为主星相对于从星的姿态矩阵。其他量测量计算方式同理，不同航天器间相对的姿态矩阵可通过转换计算得到。

量测量可用式(9)描述：

Z=h(Xform,φform,θform,ψform)+V

(9)

式中：Xform为构成量测几何中的2颗从星状态信息；φform、θform、ψform为构成量测几何中的3颗航天器姿态角信息；V为量测噪声；h(·)为量测方程。

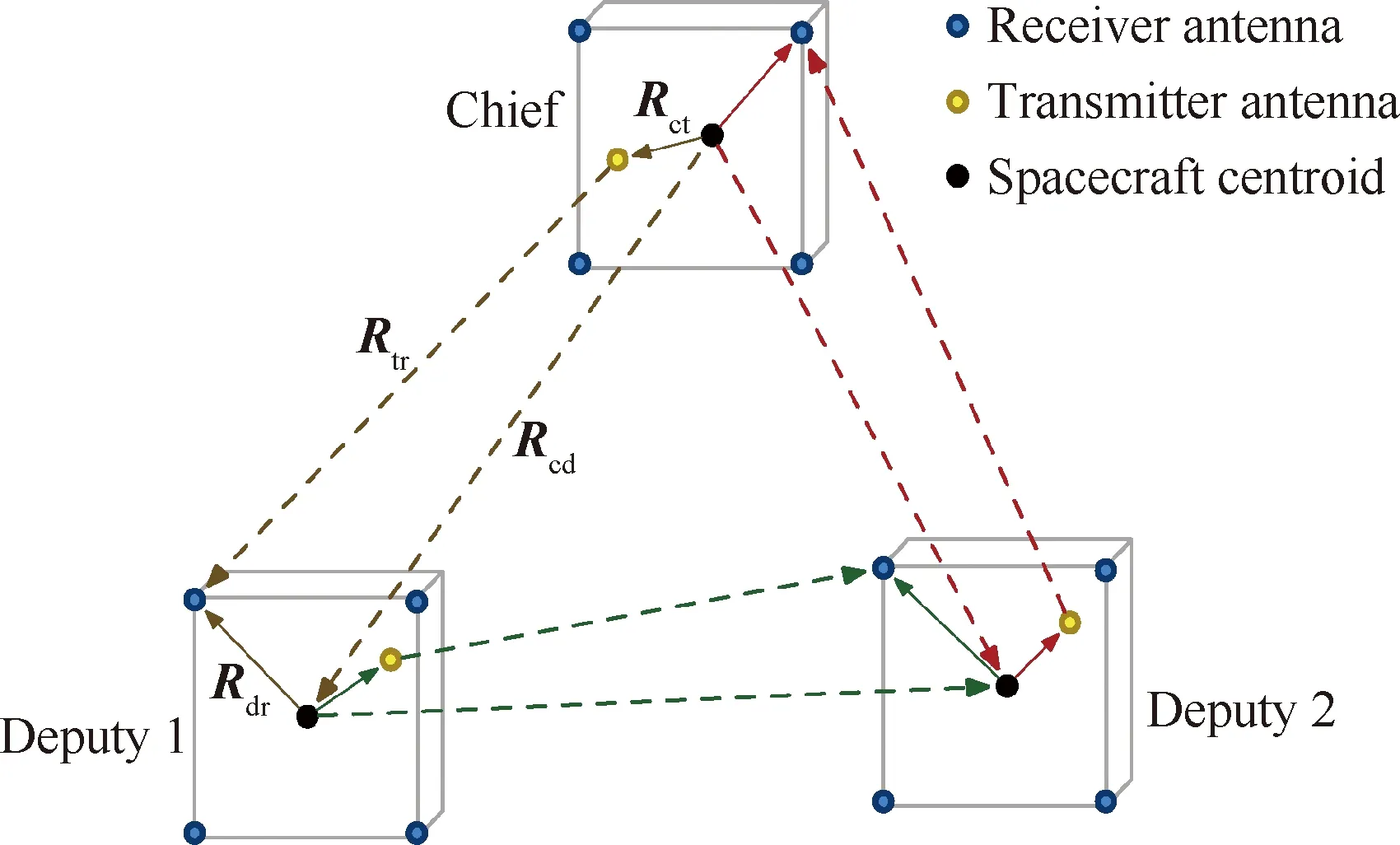
图3 量测模型示意图Fig.3 Diagram of measurement model

3 分布式相对导航的状态估计算法

根据惯性姿态已知的假设，将姿态角信息作为相对导航的输入量。

令由Deputy 1，Deputy 2，Chief组成的编队状态为

(10)

式中：X1(k)与X2(k)如式(1)所示。由式(2)得到编队的运动学方程为

(11)

式中：Φ、Γ含义如式(3)和式(4)所示；W12为Deputy 1，Deputy 2运动中的过程噪声。

令编队中的航天器姿态矩阵为M1i，M2i，Mci，分别代表Deputy 1，Deputy 2，Chief的本体坐标系相对于惯性系的姿态。由M1i，M2i，Mci可以得到

(12)

式中：M21为Deputy 2本体系相对与Deputy 1本体系的姿态矩阵；M1c为Deputy 1本体系相对与Chief本体系的姿态矩阵；M2c为Deputy 2本体系相对与Chief本体系的姿态矩阵。

因此，结合式(9)，编队的量测方程可以表示为

Z12=h(X12,M1i,M2i,Mci)+V12

(13)

式中：V12为Deputy 1，Deputy 2，Chief所组成编队的量测噪声。

采用无迹卡尔曼滤波[20](UKF)进行状态估计，UKF处理非线性模型时精度更高，计算量更小。

(14)

(15)

设计信息融合方式为

(16)

(17)

式中：W1为Deputy 1的过程噪声。Deputy 1的整个滤波过程可以用图4流程图表示。Deputy 2和Deputy 3的计算过程与Deputy 1相同。

图4 Deputy 1滤波算法流程示意图Fig.4 Flow of Deputy 1 filtering algorithm

4 算法的能观性与精度分析

本节结合仿真实验，对导航算法的能观性以及对影响导航精度的因素进行了分析。

4.1 仿真条件

在仿真实验与分析中，将过程噪声设为1 mm/s2(1σ)，将三轴姿态角估计精度设置为10″，(1σ)，分别将量测噪声设置为5 mm(1σ)和1 mm(1σ)。 仿真中滤波周期为1 s，共仿真10 000个步长。

同时，本文对安装天线的位置进行了分析，令天线安装示意图如图5所示。

令卫星模型为立方体，边长为R，则接收天线在本体系下的安装位置分别为

图5 天线安装示意图Fig.5 Diagram of antenna installation

(18)

发射天线在本体系下的安装位置为

(19)

在仿真分析时，通过改变R的值，从而改变各测量点之间的基线距离。同时，通过减少接收天线数量，研究量测值数量对相对导航精度的影响。

在静态条件下，当航天器的惯性姿态已知时，在式(8)中，唯一的未知项为三维列向量Rcd，因此求解该三维向量至少需要3个量测值。而在本文所使用的量测构型中，静态条件下共有2个航天器共六维未知项，因此至少需要6个量测值。即在量测构型的编队中，每2颗航天器之间只要有2个量测值，就可以实现静态条件下的相对位置确定。因此，在以下仿真分析中选择航天器两两间产生的量测值个数大于2。

在仿真中分别令Chief，Deputy 1，Deputy 2，Deputy 3的旋转角速度为

(20)

令Deputy 1，Deputy 2，Deputy 3相对于主星的位置、速度初始值为

(21)

仿真中令初始位置误差为5 m，初始速度误差为0.01 m/s。

4.2 仿真过程

为验证在量测构型中每对航天器之间仅有2个量测量的编队相对导航情况，设置量测精度为1 mm(1σ)，设置R为12 m，进行滤波得到在第10 000个仿真步长时3颗从星相对位置的估计误差均方差如表1所示。可以看出该条件下虽然可以实现相对导航，但是相对导航的精度较低。

表1 从星相对位置误差均方差Table 1 Standard deviation of deputies

令量测精度为1 mm(1σ)，R为12 m，每个航天器安装4根接收天线，每2颗卫星之间产生8个量测量，滤波结果和局部放大图如图6所示。由图6可以得到，位置估计误差大约为0.05 m， 速度估计误差约为5 mm/s。随着时间增加，由于航天器之间的距离增加，滤波精度下降。

图6 量测噪声1 mm时的从星估计误差Fig.6 Deputies estimation error with 1 mm measurement noise

在实际编队中，航天器之间的距离通常保持在100 m到1 000 m之间。仿真中，在初始相对速度与噪声的影响下，航天器间的距离变化如图7所示。

图7 从星与主星间的距离变化Fig.7 Distance changing between deputies and chief

第10 000个仿真步长时航天器间的距离如表2所示。可以得到仿真模型与实际编队情形相似，因此图6中的滤波精度具有参考价值。

令量测精度为5 mm(1σ)，每个航天器安装4根接收天线，滤波结果和局部放大图如图8所示由图8可以得到，位置估计误差大约为0.1 m，速度估计误差大约为10 mm/s，相较于图6，滤波精度有所下降。

分别在1 mm(1σ)和5 mm(1σ)量测精度下，设置不同的天线距离与不同数量的接收天线，3颗从星相对位置估计的标准差分别如表3、表4和图9、图10所示，其中DN表示每2颗航天器之间的量测值个数，R表示天线之间的距离，表中数组(a,b,c)分别表示Deputy 1，Deputy 2，Deputy 3的位置估计均方差。

图8 量测噪声5 mm时的从星估计误差Fig.8 Deputies estimation error with 5 mm measurement noise

表2 第10 000个仿真步长时航天器间距Table 2 Distance between spacecraft in step 10 000

4.3 仿真分析

从仿真结果可以看出，随着编队中航天器间的量测数据增加，航天器上测量点间基线距离增加，滤波精度将会增加，同时量测精度直接影响状态估计精度。

在文中仿真条件下，当编队规模在1 000 m以内，量测精度达到1 mm(1σ)时，相位位置估计的均方误差通常可以达到厘米量级。当量测精度为5 mm(1σ)时，相对位置估计的均方误差通常在0.1 m到0.3 m之间。

同时，对大量仿真数据进行分析得到，接收天线间的距离R与量测值量测精度为滤波误差的可解耦项。其他条件保持不变，仅改变接收天线间的距离R，可以得到如表5所示的结果。

表5中n1为相应R值下的滤波误差与R值为1 m下的滤波误差的比值。通过拟合，可以得到

(22)

表5中的原始数据和拟合数据的曲线图如图11所示。

其他条件保持不变，仅改变量测精度，可以得到如表6所示的结果。

表6中σ为量测噪声标准差，n2为相应σ值下的滤波误差与σ值为1 mm下的滤波误差的比值。

表3 量测噪声1 mm时位置估计均方差Table 3 Std. deviation with 1 mm measurement noise

表4 量测噪声5 mm时位置估计均方差Table 4 Std. deviation with 5 mm measurement noise

通过拟合，可以得到

n2=σ0.76

(23)

表6中的原始数据和拟合数据的曲线图如图12所示。

结合式(22)和式(23)，可以得到滤波误差同天线距离R及量测噪声的标准差σ之间的关系为

(24)

图9 量测噪声1 mm时估计均方差曲线图Fig.9 Diagram of std. deviation with 1 mm measurement noise

图10 量测噪声5 mm时估计均方差曲线图Fig.10 Diagram of std. deviation with 5 mm measurement noise

表5 不同天线距离下的滤波误差比例Table 5 Proportion under different antenna distances

图11 滤波误差与天线距离的关系拟合图Fig.11 Relationship between filtering error and antenna distance

表6 不同量测噪声下的滤波误差比例Table 6 Proportion with different measurement noise

图12 滤波误差与量测噪声的关系拟合图Fig.12 Relationship between filtering error and measurement noise

式中：ε为估计误差；F(others)为与其他项(如卫星运动状态，天线数量，天线安装构型)有关的数值。通过式(24)，可以快速求出在其他项不变时，不同量测精度及不同天线距离下的估计误差。

5 结 论

研究了日地L2点深空探测航天器编队的相对导航问题，提出了一种基于局部测量信息的分布式自主导航方法，通过生成测量构型、滤波、融合3个步骤来确定从星相对于主星的状态信息。只采用局部测量信息降低了估计状态的维度，提高了计算效率，同时通过信息的融合提高状态估计的精度。还对影响相对导航精度的因素进行了研究分析，得到以下结论：

1) 显然量测值的数量越多，滤波误差越小，相对导航精度越高。但误差的下限值受多方面因素影响，当每对航天器间的测量量大于4个的时候，对于精度的提升不明显，因此，使用本文的方法进行相对导航时，建议安装4个接收天线。

2) 在相同安装构型下，接收天线间的距离越远，即测量点间的基线越大，会有更高的相对导航精度，基线距离为滤波误差的可解耦项，文中给出了拟合经验公式。

3) 随着编队中航天器的距离增加，相对导航精度将会下降。当航天器之间的距离在500 m以内时，通常可以保持0.01 m(1σ)左右的位置估计误差；当航天器之间的距离增加到1 000 m左右时，位置估计误差逐渐逐渐上升至0.03 m(1σ)。

4) 测距精度将直接影响最终的相对状态估计精度，测距精度为滤波误差的可解耦项，文中给出拟合经验公式。