恶劣天气条件下航路网络修复优化

隋东，邢娅萍，涂诗晨

南京航空航天大学 民航学院，南京 211106

由中国民用航空局官方统计数据[1]可知，2014—2018年间天气原因导致的航班不正常率从24.30%增长到47.46%，在2016年和2017年甚至超过了50%，相比空管、航空公司和其他因素，天气已成为影响航路网络正常运行的第一因素。恶劣天气导致航路网络部分拓扑结构失效时，预计经过失效结构的航班运行受到影响，极易造成大面积的航班延误。通常采用两种策略应对航班不正常运行问题：一是调整航班的飞行路径，以改航为主，该策略虽能有效缓解航班延误，但临时航线的启用往往需要多方密切协调和及时的信息传递，且改航路径一般较长，会使航班的飞行成本大幅度增加；二是调整航班离场时间，以地面等待为主，该策略将空中延误转为地面延误，能够有效降低航班延误总成本，却不利于降低航班延误率。

国内外许多学者已经从各个角度对恶劣天气下的航班延误问题进行了深入研究，本文试图从航路网络修复这一角度入手研究航班延误缓解问题。航路网络修复是航班原有计划路径因突发事件影响而失效时，寻找一条避开流量受限区的修复路径，使航班在修复路径上运行以缓解航班延误。传统导航方式下，航空器沿着导航台运行，导航台位置和其他相关设备会影响航路的布局，2008年国际民航组织提出的基于性能的导航(Performance-Based Navigation，PBN)能够将飞机先进的机载设备与卫星导航及其他先进技术结合起来，覆盖航路、终端区到进近着陆的所有飞行阶段，使航班可以沿任意期望的航迹运行[2]。未来星基导航和其他先进技术的逐渐成熟将大大促进PBN技术的广泛应用，从而为航路网络修复策略的实施奠定基础应用环境。目前针对航路网络修复的研究较少，但是针对复杂网络修复的研究已经比较广泛，而航空运输事业的发展使航路网络逐渐呈现出复杂网络的特性，因此航路网络修复研究可借鉴复杂网络领域的相关研究。2000年Kodialam和Lakshman提出了一种局部信息修复策略，以工作路径上的链路带宽最大值为基础建立链路共享权重函数，选择一条从源节点到目的节点之间权值和最小的路径代替故障路径，该修复策略相比最短路径算法具有一定的共享性[3]。2003年Li等提出了一种全局信息修复策略，该策略相比Kodialam和Lakshman的研究将最大带宽值替换成了带宽矩阵，弥补了局部信息修复策略容易陷入局部最优的不足[4]。许多学者在此基础上进行拓展和延伸，缪志敏等将基于拓扑图论的修复策略总结分为3类：基于拓扑分割子网的网络修复算法、基于拓扑结构的路径修复算法和基于链路的修复算法[5]。以上修复策略都是基于网络原有拓扑结构进行研究的，也有很多研究通过在网络中增加边的方式修复受损网络。按照是否与受损节点的邻接节点相关将增边策略分为两类：一是在重要度比较高的节点之间增加连边；二是在受损节点的邻接节点上增加连边。关于在重要度高的节点之间增边修复的研究最初有2005年Beygelzimer等提出的通过随机加边、偏好加边、随机边重新布线、随机邻边重新布线、优先布线和优先随机边重布线6种添加边的方法改善网络的拓扑结构[6]。后续很多网络修复研究都是在文献[6]研究基础上展开的，如2014年Zhang等将任意一对没有连接的节点i、j的权值设为介短函数(BiBj/Lij)，其中Bi为节点i的介数值，Lij为节点对i、j的最短距离，选择在权值最小的节点对增加连边来对受损网络进行修复[7]。2018年齐小刚等提出了一种最大化网络平均效率的加边策略，节点受攻击后，每一次添加的链路都使得网络平均效率值增加值最大，直到添加链路数达到指定数量[8]。关于在邻接节点上增边修复的研究有2005年Hayashi和Miyazaki介绍的两种基于邻接节点互连的网络修复策略，解决了节点受损导致的连边受损问题[9]。而后不少学者从连边补偿角度研究网络修复策略，如2016年Ma和Han将新增边的权值从节点度值和变为考虑受损节点邻接节点的权值函数wiwj/L′ij，其中wi为节点i与其邻接节点的度值乘积之和，L′ij为节点i的局部度值，选择权值最小的节点连边加入网络中[10]。总体而言，可将复杂网络修复策略按照是否调整网络拓扑结构分为两类：① 网络受损后，在原有拓扑结构中寻找修复路径，使资源在修复路径上运输，称为原有拓扑结构修复策略(Repair Strategy based on Original Topology，RSOT)；② 网络受损后在网络中增加新连边，使资源在带有新边的修复路径上传输，称为拓扑结构调整修复策略(Repair Strategy based on Adjustment Topology，RSAT)。RSOT的修复成本较低，但其修复效果极其依赖网络未受损结构，因此该策略不一定使网络整体达到最优修复效果。RSAT能够在优化网络拓扑结构的同时有效提升网络性能，然而新路段的引入往往伴随着协调难度大、信息发布反馈不及时等问题，可能导致修复成本成倍增大。

恶劣天气条件下的航路网络受损，往往受损面积和影响范围较大，RSOT可能很难在未受损的结构中找到最优的修复路径；RSAT引入新的航段对整个航路运行会产生一定的影响，所以无论是单独利用RSOT策略或RSAT策略求解，对于受恶劣天气影响的航路网络的修复效果并不理想。

本文将结合两类复杂网络修复策略，借鉴离散网络设计理论，提出航路网络修复优化策略。该策略下部分航班采用RSOT，在已有航段构成的修复路径上运行；剩余受影响航班则采用RSAT，在带有新航段的分流路径上运行。该修复优化策略将：① 考虑航段距离、转弯角度和容量均衡等多重约束对同一受损路径上的航班进行分批修复；② 在网络中引入少量新航段，建立以最低修复成本为目标函数的双层修复优化模型，修复成本包含飞行成本增量和协调成本，分别表示对正常运行航班的干扰程度和新航段的启用难度，最低修复成本意味着修复策略对正常运行航班干扰足够小且航路网络调整尽可能小；③ 有利于增大理想路径的搜索效率，且能够有效剔除距离较长的分流路径。

1 航路网络修复场景

1.1 恶劣天气飞行受限区

在航空领域，恶劣天气包含雷暴、积冰、闪电、冰雹、下击暴流、低空风切变和暴雨等会影响航空器安全飞行的天气。以雷暴为恶劣天气的典型代表展开研究，原因如下：① 在诸多恶劣天气中，对航路飞行造成严重影响的主要天气是雷暴；② 雷暴强度可以用雷达基本反射率量化表示[11]，这一气象产品可由多普勒气象雷达获取，其他恶劣天气如积冰、颠簸和风切变等很难量化。

所以恶劣天气飞行受限区可以用雷暴的范围来表示，由于雷暴的范围通常呈现不规则的形状，通常使用规则的图形规划雷暴的边界，常用的方法包括外接法[12]和凸多边形算法[13]，并且根据雷达反射率的大小来判断雷暴的恶劣程度，雷达反射率大于等于41 dBZ的区域是禁止航班穿越飞行的[14]，即为恶劣天气飞行受限区。本文采用Graham算法[15]对不规则的恶劣天气受限区进行规则化界定。

1.2 航路网络修复范围

恶劣天气发生具有局部性和随机性，航路网络修复在局部范围进行。航段和航路点失效后，假定当前航段和航路点都不可直接修复，尤其是航路点失效后，与之连接的航段因无法完成运输任务而自动失效。恶劣天气对航路网络攻击形成3种失效状态，如图1所示，多边形区域是恶劣天气飞行受限区。

第1类修复范围：恶劣天气发生在某一航段上，航段连接的航路点没有受到影响，如图1(a)所示，此时航段AB失效，经过该航段的航班在航路点AB之间寻找修复路径。

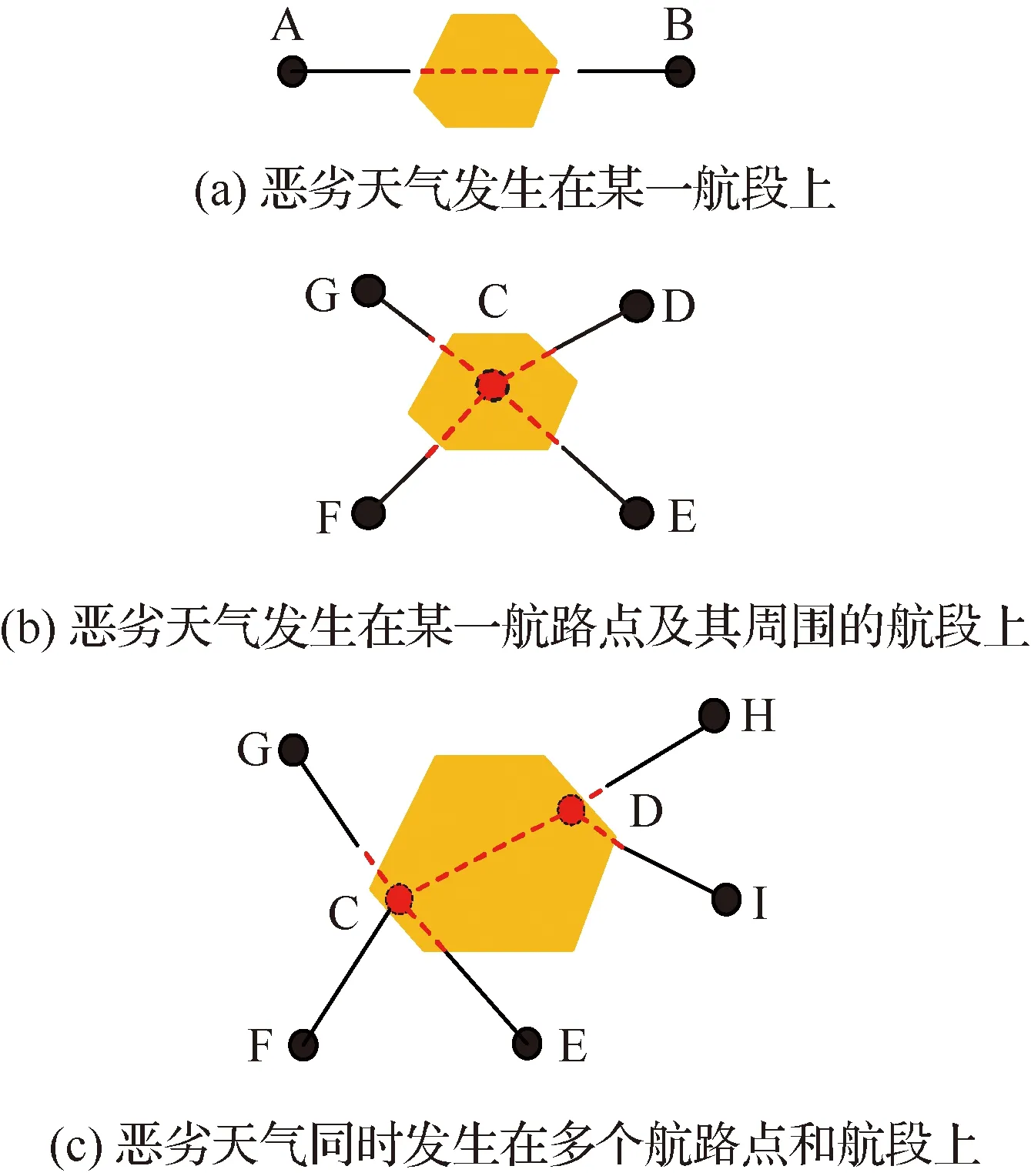
图1 航路网络的3种受损模式Fig.1 Three disrupted modes of air route network

第2类修复范围：恶劣天气发生在某一航路点及其周围的航段上，邻接节点未受影响，如图1(b)所示，此时航路点C失效，航段CD、CE、CF和CG都失效，经过航路点C的航班在其邻接节点之间寻找修复路径。

第3类修复范围：恶劣天气同时发生在多个航路点和航段上，如图1(c)所示；此时航路点C和D失效，与两个航路点相连的航段也失效，经过航路点C和D的航班在其周围完好的节点对之间寻找修复路径。

为了有效搜索受影响航班的修复路径，将修复路径的起终点定义为有效起讫节点对。对受损航段而言，优先选择当前航段的两端航路点作为有效起讫节点对；对受损航路点而言，优先选择故障节点周围未受损的邻接节点作为有效起讫节点对。

1.3 修复路径备用航段

同一个有效起讫节点对在采用不同修复策略时对应的备用航段集是不同的。RSOT中备用航段集由原有航路网络中未受恶劣天气影响的航段组成。RSAT将航路网络变成全联通网络，删除经过恶劣天气飞行受限区的航段、航路点以及受损航路点连接的航段后，剩余航段组成备用航段集。

2 航路网络修复优化策略

离散网络设计问题(Discrete Network Design Problem，DNDP)主要是从备选路段方案中选择一个最优的路段添加方案添加到现有网络中，使得网络系统性能更优，以某一路段为例，将其添加到现有网络时，决策变量为1，反之决策变量为0[16]。将其思想应用于航路网络修复问题，假设有n个有效起讫节点对之间的航班需要进行重分配，每个有效起讫节点对有两种选择方式，选择RSOT时，决策变量值取0；选择RSAT时，决策变量值取1。n个有效起讫节点对的选择对应2n种决策方案，不同决策方案用Uy(y= 1,2,3,…,2n)表示。

航路网络修复优化策略(Repair Optimization Strategy，ROS)是从2n个决策方案中选择最优的方案，使得总修复成本最低。假设受损网络为G0，原有航段集为A0，航班重分配的有效起讫节点对集合为Pnode。假设有x对选择RSOT，对应有效起讫节点对集合为Nx，对应修复路径上的航段集合为A1。剩余l(l=n-x)对起讫节点选择RSAT，对应有效起讫节点对集合为Nl，对应修复路径上的航段集合为A2，Nx∪Nl=Pnode。航路网络的修复优化模型可描述为双层整数规划模型。

2.1 模型搭建

2.1.1 上层模型

上层模型以航路网络修复成本最小为目标。修复成本共包含两部分：一部分是航空器相比原有飞行路径在分流路径上运行增加的飞行成本费用，飞行成本费用越小，对原有未受影响航班的干扰越小；另一部分是新增航段带来的空域协调、通信等的综合协调费用。

上层模型用公式表达为

(1)

(2)

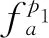
2.1.2 下层模型

下层模型为多约束非均衡分配模型，以有效起讫节点对上的修复路径距离和最小为目标，在容流平衡约束、流量重分配约束、角度约束和转弯约束等多重约束下，寻找修复路径完成交通流分配。

(3)

(4)

(5)

θ≥ 90°

(6)

dij≥ 7.4 km

(7)

(8)

(9)

式(4)为容流平衡约束。有效起讫节点对s,t之间任意一条路经上的交通流量应小于等于路径上的最小航路点容量，在这里容量为航路点通行能力。

式(5)为流量重分配约束。有效节点对s,t之间共有M条路径用于交通流重分配，前M-1条路径上的重分配流量等于当前路径的冗余容量，最后一条路径上的重分配流量小于等于该路径的冗余容量。

式(6)为角度约束。出于航路安全飞行角度考虑，航段之间的夹角θ应大于等于90°，即航空器航向的最大改变量应小于等于90°[17]。

式(7)为转弯约束。为满足转弯安全性要求，航段长度应大于7.4 km[18]。

式(8)为航段流量。

式(9)为非负约束，即模型中所有变量都非负。

2.2 模型求解

粒子群优化(Particle Swarm Optimization，PSO)算法属于启发优化算法，因概念简单、参数少，求解简单快速，计算结果精度高偏差小，应用十分广泛，因此采用PSO算法求解修复优化模型。

2.2.1 PSO算法求解

粒子的速度、位置和权重因子按照式(10)～式(12)进行更新[19]：

(10)

(11)

(12)

基于IPSO的修复优化模型的求解步骤如下：

Step 1初始化设置。设置最大速度Vmax，最小速度Vmin，最大惯性权因子wmax，最小惯性权因子wmin，加速常数c1、c2，初始粒子数为m，最大迭代次数T，位置最大值Zmax，位置最小值Zmin，粒子的初始位置z0和初始速度v0。

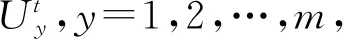
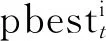
Step 5重复Step 2～Step 4，直到达到指定迭代次数，输出群体最优适应度和最优位置。

2.2.2 下层模型求解

下层模型为多约束交通流分配模型，采用K最短路径算法在多重约束下寻找两节点之间的多条较短路径，常用Yen’s算法求解[21]。在找到两节点对之间的m条路径后，将有效起讫节点对之间的交通量按照每个路径的冗余容量大小分为m份分配，在分流路径不足或者找不到分流路径时，对应航班选择地面等待策略。计算步骤如下：

Step 1根据恶劣天气影响范围寻找所有的有效起讫节点对，将其存于集合Pnode中，假设共有num个有效起讫节点对。

Step 2根据转弯约束，删除备用航段集中长度小于7.4 km的航段，构建可用备用航段集合。

Step 3基于可用备用航段集，采用Yen’s算法计算有效起讫节点之间的前K条最短路径，存储于集合Path中。

Step 4根据角度约束，删除Path中存在航段夹角小于90°的路径，更新集合Path。

Step 5根据流量重分配约束，判断有效起讫节点对流量重分配需要的可用路径数。

Step 6对于有效起讫节点对，若可用路径数不足，适当增大K值，令K=rK，其中r为增大系数，取值随实际情况而定，重复Step 4～Step 6，若可用路径数仍然不足，该节点对之间的部分航班选择地面等待策略。

Step 7可用路径足够时，将有效起讫节点对之间的所有受损航班按照每条可用路径的冗余容量值进行分批重分配，重复Step 4～Step 7，直到num个有效起讫节点对都结束运算。

需要注意的是，在RSAT中，将航路网络变成全联通网络只是为了增大备用航段集，在对受损航班重分配后，受损航路网络中增加的航段只有修复路径上的新航段，而非RSAT下备用航段集中的所有航段。

3 仿真实验

3.1 案例航路网络描述

航路网络由航路点和使得网络连通的航路组成。航路点包含各类导航台和多种交叉点，航路点两两连接构成航段，多个航段连接形成航路。在构建航路网络模型时将航路点和航段简化在二维平面中，忽略孤立航路点。根据复杂网络理论，假设航路点是网络中的节点vi，航段是网络中的边或者链接eij。将航路网络记为G={vi,eij,n}，其中n取值为0或1(若任何两个航路点vi、vj间存在航段，则n=1；反之n= 0)。

3.1.1 案例网络拓扑结构

根据2018年中国民航国内航空资料汇编更新的航行信息，统计上海市、江苏省、安徽省、江西省、浙江省和福建省6个地区范围中的航路点和航段，构建成案例航路网络。案例航路网络由246个航路点、361条航段构成。

3.1.2 运行数据

为深入研究恶劣天气对航路网络运行的具体影响，需要对航路网络上的交通流分布进行统计。7、8月份是一年中雷暴发生比较频繁的时段，选取2018年8月份的案例航路网络上的航班飞行计划数据作为仿真运行数据。

流量高峰时段的航路网络运行状态相比其他时段更加复杂，对繁忙时段的航路网络受损修复进行深入研究，将更有利于受损航路网络的快速恢复。选取2018年8月16日交通流高峰时段的案例航路网络运行数据为仿真数据。统计当天00:00～24:00之间的小时航班总量，发现8:00～10:00之间的交通量是最多的，共有752个航班正在运行。故后续仿真实验以8:00～10:00之间的航班运行数据为基础数据。

3.1.3 仿真环境

利用Windows 10操作系统中的MATLAB2017a软件进行编程，在处理器为Intel®CoreTMi7-7700、内存为16 G的PC机上进行仿真，仿真采用2018年8月的历史雷达轨迹数据、气象数据以及全国航路网络结构数据构建恶劣天气条件下的受损航路网络。

在确定空域中恶劣天气飞行受限区后，计算案例航路网络的受损航段和航路点，图2为案例航路网络的受损状况，图中红色多边形覆盖的区域是恶劣天气发生的区域，其具体信息如表1所示，航路网络小面积受损会导致将近1/3的航班不正常运行，也反映了恶劣天气对航路网络运行的影响程度。

图2 案例航路网络的受损状态Fig.2 Disrupted state of typical air route network

表1 航路网络受损信息Table 1 Information of disrupted air route network

3.2 航路网络修复优化仿真

3.2.1 修复成本系数设置

飞行成本系数α为单架航空器单位距离上的飞行成本，用航路使用费计算。2012年中国民用航空局联合国家发展改革委发布了《关于调整民航进近指挥费和航路费有关问题的通知(民航发[2012]59号)》，其中规定了内地航空公司国际及港澳航班航路收费标准。本文按照最高收费标准取α= 1.5 元·km-1·架次-1。

以飞行成本系数为基础，假设协调成本系数β= 2.0 元·km-1·架次-1。在协调成本系数的基础上，考虑到交通流密度对航班飞行的影响，认为协调难度系数γ与航段交通量f相关，交通量区间不同，协调难度系数不同。修复成本系数设置如表2所示。

表2 修复成本系数设置Table 2 Settings of repair cost coefficient

3.2.2 有效起讫节点对和备用航段集

1) 有效起讫节点对

根据1.2节的定义，计算案例网络受损后的有效起讫节点对，共有15对，相关信息如表3所示。分别采用RSOT和RSAT寻找所有有效起讫节点对的修复路径，发现有效起讫节点对“ADGOL-KIKEG-HFE”和“ADGOL-VILID”在采用RSOT时，找不到分流路径，而在RSAT下，这两个节点对都能找到对应的分流路径，故这两个节点对默认采用RSAT，不参与修复优化。RSAT中有效起讫节点对“SHZ-BK”之间的分流路径与RSOT相同，默认该节点对采用RSOT，不参与修复优化。故修复优化仿真实验中有12个有效起讫节点对，对应着4 096种决策方案。

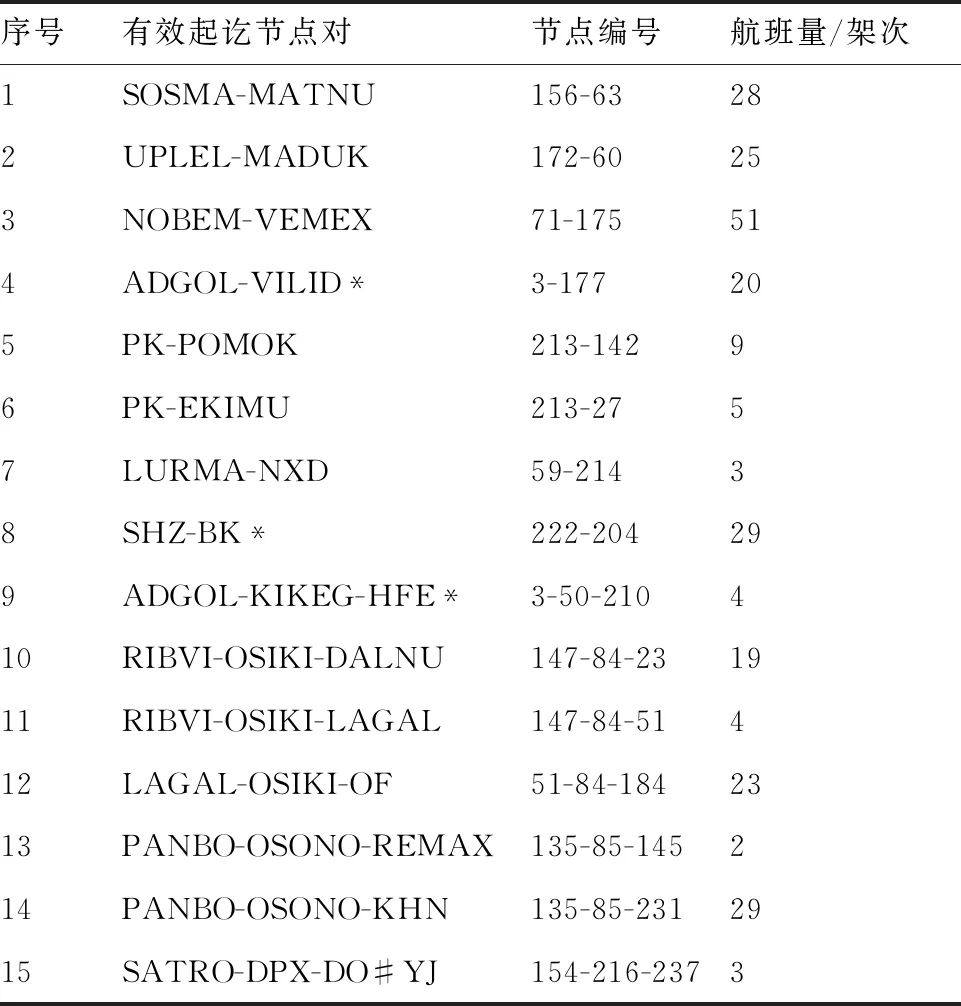
表3 有效起讫节点对信息Table 3 Information of valid origin-destination nodes

2) 修复备用航段集

根据2.2节计算不同修复策略下的修复路径备用航段，RSOT下的可用航段数为325条，RSAT下的可用航段数为19 818条。

3.2.3 航路网络修复优化结果

随机生成20个粒子，初始化粒子速度，将每个粒子的位置代入下层模型求解航段交通量和路径距离，反馈到上层计算适应度值，根据式(10)～式(12)更新各粒子的速度和位置，迭代1 000次后得到最低修复成本，运算耗时3 763 s。

IPSO参数设置如表4所示。

表4 IPSO参数初始化设置Table 4 Initial settings for IPSO parameter

图3为粒子适应度曲线，可以发现IPSO求解该模型时收敛较快，在第63次计算时群体适应度达到最优，在图中用实心三角形标注，此时修复成本为75 016.65元，适应度对应位置为‘705’，对应决策方案为U=‘001011000001’。

图3 IPSO迭代适应度曲线Fig.3 Iterative fitness curves of IPSO

将不参与修复优化决策的3个节点对对应的决策变量并入最终的决策方案中，最优修复决策方案变更为U*= ‘001101101000001’。将最优决策方案的具体情况列入表5。

表5 最优决策方案Table 5 Optimal decision scheme

3.3 结果分析

以“PANBO-OSONO-REMAX/KHN”有效起讫节点对为例，对修复策略进行详细说明。由于OSONO航路点受到较大面积的恶劣天气的影响，导致OSONO航路点连接的航路也受到影响。有广州飞往南昌以及广州飞往南京的两个航班，其原本飞行路径分别为“PANBO-OSONO-REMAX”和“PANBO-OSONO-KHN”，3种修复策略得到的修复路径如表6所示，详细路径如图4所示，从不同策略生成的修复路径可以很直观地看出，ROS修复策略相比于其他两种修复策略对恶劣天气影响下航路网络修复更有效，飞行距离更短，如在广州飞往南京的飞行路径选择上，RSAT比RSOT和ROS修复策略更长，而在广州飞往南昌的飞行路径选择上，RSOT比RSAT和ROS修复策略更长，相比之下，ROS修复策略的经济性更好。

分别采用两类基础修复策略对受损后的航路网络进行修复，将修复结果与修复优化策略结果进行对比分析，同时还将计算结果与真实运行情况进行对比，以验证修复优化策略的有效性。从局部和全局两个角度出发，评估不同修复策略下航路网络的运行状态。

从局部角度来看，能够直接反映不同修复策略有效性的指标为受损航班恢复比例。修复成本反映了修复策略下航路网络运行增加的额外成本，但其不能反映修复策略对整个航路网络运行性能的影响，其和受损航班恢复比例属于评估网络局部变化的指标。

表6 3类修复策略的案例分析Table 6 Case analysis of three types of repair strategies

图4 3类修复策略案例Fig.4 Case of three types of repair strategies

从全局角度来看，通过运算耗时评估不同修复策略的计算速度和实效性。通过计算整体运行环境的延误时间对比反映不同修复策略对恶劣天气的应对能力。网络运行效率[22]反映不同情况下网络性能的变化，可反映修复策略对航路网络整体运行的影响。计算公式为

(13)

式中：Ef为网络运行效率；fx,y为节点x、y之间最短路径上的运行航班量。

表7中详细列入了3类修复策略与实际运行情况对应的指标值。

从航班恢复比例来看，ROS和RSAT下航班恢复比例相同且大于RSOT对应的值。RSOT下航路网络备用航段数较少，部分航班找不到分流路径，无法恢复正常运行；RSAT和ROS中新航段的引入增大了搜索范围，加快了搜索效率，使得所有受天气影响的航班都能找到有效分流路径。

从修复成本来看，ROS下航路网络修复成本最低，其次是RSOT，RSAT下航路网络修复成本最高。有效起讫节点对之间的交通量是固定的，RSOT基于原有网络结构进行修复，生成的分流路径大多长于计划飞行路径，航班飞行成本也对应增大；RSAT引入了部分新航段，分流路径相比RSOT大多较短，然而新航段带来了高额的协调费用。ROS采用离散网络设计思想将两类基础修复策略结合在一起，避免了使用距离较长的航段，也减少了新航段的数量，修复成本相比RSOT和RSAT都低。

从总延误时间来看，RSAT下的总延误时间最短，其次是ROS，RSOT下总延误时间最长。总延误时间能够反映出在不同修复策略下的航路网络对于特殊情况的应对能力，总延误时间越短，应对能力越强，遭遇恶劣天气时，RSAT引入部分新航段，能够立即做出反应，而RSOT只能针对未受损网络结构进行修复，相比之下应对能力较弱。ROS将两种策略结合，一定程度上提高了对特殊情况的应对能力。但无论哪种修复策略，相比于实际运行情况，航路网络的应对能力均得到了改善。

从网络运行效率来看，RSOT下航路网络的运行效率最高，其次是ROS，RSAT下航路网络的运行效率最低。运行效率反映了航路网络中交通流分布的聚集特征，也反映了修复策略对受损航路网络运行水平的影响。可以发现，采取RSOT后，航路网络流量分布有很强的聚集性，ROS次之，RSAT集聚性特征是最弱的。交通量分布的聚集性高意味着对应管制扇区内管制员工作负荷较大且容易过载，航路拥堵风险大和航空器冲突概率高。修复策略RSAT和ROS能够将交通流分散到流量相对少的航段，有利于降低航空器冲突和航路拥堵概率，从而减缓航班延误程度。

综合考虑认为ROS是适用性最好、经济性最佳的修复策略，其在使用最低修复成本使所有受到影响的航班都恢复正常运行的情况下，保证了整个航路网络的高效畅通运行。

4 结 论

1) 针对恶劣天气条件下的航路网络修复问题，将RSOT和RSAT两种修复策略结合，避免了RSOT过于依赖网络未受损结构以及RSAT由于协调难度大而导致的修复成本增加的问题，有效地综合两种修复策略的优势，提高了网络性能。

2) 航路网络修复优化策略不再简单以路径最短或者风险最低为修复目标，而是考虑到航班运行经济成本，基于DNDP思想建立了双层规划优化模型，上层以修复成本最低为目标，下层以满足多重约束的路径最短为目标，充分考虑了航班恢复运行的安全性、经济性、可行性和畅通性，同时该模型在满足“四性”的基础上，相比两类基础修复策略，既能合理利用原有拓扑结构，又能解决新航段产生巨额协调费用的难题，在网络修复成本最低的情况下，有效地提高了网络的运行性能。

3) 应用IPSO求解修复优化模型的优点有：作为启发式算法，IPSO中需要设置的参数很少，减小了因参数设置不合理导致求解结果不准确的可能性；解编码的存在解决了传统PSO算法很难求解离散网络设计问题的难点；IPSO解决了枚举法只能求解小规模问题的局限性。

4) 从局部和全局两个角度评估了修复优化策略的有效性和优越性。局部指标包含航班恢复比例和修复成本，这两个指标反映了修复优化策略对受损航班运行的修复效果，也体现了修复优化相比两类基础修复策略的优越性；全局指标为运算耗时、总延误时长和运行效率，反映了修复优化策略对航路网络运行的整体作用。相比于其他修复策略，该策略下航路网络上交通流的聚集性一般，对于减缓航路拥堵和航班延误、减轻航空器延误都十分有效，提高了航路网络对特殊情况的应对能力。

5) 研究给未来恶劣天气下航路网络的畅通运行提供了修复技术支持，对于减缓航路拥堵和航班延误有极大的意义。但本文仅针对恶劣天气条件下航路网络修复这一问题的解决策略开展研究，尚未涉及运行层面的相关细节。在对修复策略的实际应用方面，需要针对运行中的相关问题，如气象的动态变化趋势、扇区边界约束以及航路运行限制等等，开展更深入的研究和分析，进一步提高航路网络修复优化策略的实用性。

[21] YEN J Y. Finding theKshortest loopless paths in a network[J]. Management Science, 1971, 17: 712-716.