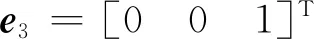一种改进的运载火箭迭代制导方法

2021-03-26马宗占许志唐硕张迁

航空学报 2021年2期

马宗占，许志,*，唐硕，张迁

1. 西北工业大学航天学院，西安 710072 2. 陕西省空天飞行器设计技术重点实验室，西安 710072

提高可靠性并降低成本已成为当前运载火箭发展的两大趋势。SpaceX的“猎鹰9”火箭在主动段飞行时，当9台发动机中的2台出现故障时依然能够准确将有效载荷送入预定轨道[1]，这要求其制导算法必须具备高精度、强鲁棒性和对非灾难故障状况的适应能力[2-3]。

从20世纪60年代开始，基于最优控制理论的迭代制导算法便已经应用于运载火箭大气层外制导，该算法由于不依赖于标准轨迹，只基于当前飞行状态和目标轨道参数迭代计算出最优入轨指令，因此该算法对参数不确定性都具有较强的适应能力。早期土星火箭采用基于线性正切形式的迭代制导算法(IGM)[4-5]，该算法将引力场假设为常值，通过把制导指令分解成俯仰和偏航两个平面(假设偏航指令为小量)来简化迭代流程。20世纪 70年代初，为了适应航天飞机多任务制导要求，Brand[6]和Long[7]等在IGM算法的基础上，开发了动力显式制导(PEG)算法[6-7]，该算法将三维推力矢量作为控制量，以正交假设代替横截条件，对推力积分做线性化展开，以剩余速度作为迭代变量，并引入推力可调模式等处理手段，这使得该算法相比于IGM在最优性和任务适应性上具有更大的优势。Jaggers[8-9]、Von der Porten[10]等对PEG算法进行了改进，采用线性引力场假设，控制量限幅和修改雅克比矩阵等措施进一步增强了算法的最优性和收敛性。而陈新民和余梦伦[11]在推导最优解时用3个速度分量和2个位置分量约束代替轨道根数约束从而简化了横截条件，茹家欣[12]在此基础上增加了迭代入轨点纬度幅角，进一步保障了算法的收敛性。上述迭代制导算法都是降维迭代的方式求解最优控制量从而保障算法收敛，但由于采用了简化假设代替准确的横截条件而难以保证算法最优性，并且在进行推力积分时假设与位置约束相关的控制量为小量进行线性化处理导致降低了积分精度，这两点不足使传统迭代制导难以在推力大幅下降情况下保障其最优性和故障适应性。

与迭代制导方法不同，Brown等在1967年提出的最优制导(OPGUID)方法[13-14]采用线性引力场假设并严格满足所有最优性条件，以协态变量和剩余时间作为迭代变量，采用多维Newton-Raphson法进行求解。Lu和Dukeman等则对最优制导算法在计算和求解上进行了改进[15-17]，并将其应用拓展到了大气层内和助推-滑翔-助推模式。而文献[18-20]则通过推导了牛顿法中Jacobi矩阵的解析表达式对求解过程进行了改进，并推导了基于轨道要素形式终端约束的边界条件。与迭代制导相比，最优制导方法尽管保留了完整的最优性条件，但对初值的敏感性和多维迭代的低收敛特性也给算法在线应用带来了较大的风险[21]，因此严重制约了其工程应用。

针对火箭推力故障情况下迭代制导在最优性和故障适应性上存在的局限性，本文提出了一种改进迭代制导算法。该算法重新推导了基于火箭最优入轨问题的具有5个终端轨道根数约束的横截条件，提高了算法最优性；采用高斯-勒让德方法提高推力积分精度；最后该算法保留了迭代制导的降维求解模式，并结合控制量限幅算法，进一步保障算法实时性和收敛性。本文算法通过能够迭代出新的入轨点真近点角进而保障火箭入轨，对推力故障具有更强适应性。

1 火箭入轨最优控制问题

1.1 火箭动力学模型

本文在入轨点坐标系O-XYZ下建立的火箭飞行动力学模型，入轨点坐标系定义如图1所示：坐标原点取为地心，OY轴指向参考入轨点，在惯性空间内固定，OX轴在轨道平面内，垂直于OY轴，指向卫星运行方向，OZ轴、OX轴和OY轴组成右手坐标系。图中O-XIYIZI为地心赤道惯性系；i*为目标轨道的轨道倾角；w*为近地点幅角；Ω*为升交点赤经；f*为参考入轨点真近点角。

火箭在大气层外飞行动力学方程为

(1)

式中：u为单位推力矢量；T为常值推力大小；Vex为发动机比冲。采用线性引力场假设

g=-ω2r

(2)

式中：ω为平均角速度，取作当前位置矢径r0与入轨点矢径rf模的平均值处的圆轨道角速度，即

(3)

式中：μ为地球引力常量。

1.2 最优控制问题描述

火箭入轨最优控制问题描述为：寻找u(t)，使火箭沿着该推力方向可以在满足一定约束条件下以最小燃料消耗量进入指定的轨道。由于推力大小一定时，性能指标最小燃料消耗可以等效为最短入轨时间，因此该最优控制问题的状态变量微分方程为方程组(1)中前两式，性能指标为

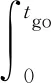
(4)

式中：tgo为剩余飞行时间。终端约束(通常以轨道根数形式给出)用状态量表示为

Ci(vf,rf)=0i=1,2,…,n(n<6)

(5)

式中：下标f表示终端值(下文同)。控制量约束为

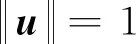
(6)

对于该最优控制问题，可以利用变分法相关理论，将其转化为终端时间自由的两点边值问题。

1.3 最优控制问题求解

本文应用极大值原理[22]求解最优控制量，选择的哈密尔顿函数为

(7)

式中：λr、λv为协态变量。根据极大值原理解得控制量为

(8)

协态变量为

(9)

(10)

1.4 5个轨道根数约束下的横截条件推导

火箭入轨一般需要满足5个轨道根数形式的终端约束，即半长轴a、偏心率e、轨道倾角i、升交点赤经Ω以及近地点幅角w。最优控制解不仅需要满足5个轨道根数的终端约束，还需要满足相应的横截条件。对于终端时间自由的两点边值问题，其横截条件的表达式为

(11)

Hf=0

(12)

式中：ηi为拉格朗日乘子，终端约束Ci的表达式见附录A。其中约束(12)可以由式(13)代替[14]

(13)

而式(11)是一组6维方程组，无法直接用于迭代制导，因此下文将对其进行降维处理。将Ci(i=1,2,…,5)的表达式代入式(11)中的前两式得到

λf=-η1vf-η2(rf×vf)×rf-η4e3-

η3[2vf(rfN)-rf(vfN)-(rfvf)N]

(14)

(15)

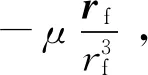
(16)

在式(15)两端同时点乘vf，得到

(17)

用式(16)减去式(17)即可消去拉格朗日乘子，得到

(18)

式(18)即为第一个横截条件的表达式。传统迭代制导方法通常用简化假设代替这一约束条件，如PEG采用正交性假设[7]

(19)

而文献[12]用3个速度分量和2个位置分量约束代替5个轨道根数约束，即令

(20)

式(20)和下文中标量加下标X、Y、Z均分别表示对应矢量在入轨点坐标系下的X、Y、Z坐标。由式(11)和式(20)得到

(21)

从而代替式(18)。本文则保留了式给出的准确横截条件，消除了PEG及文献[12]等对横截条件的假设，从理论层面上提升了算法最优性。

2 迭代过程推力积分计算

定义推力积分为

(22)

(23)

由式(8)和式(10)得到最优推力单位矢量的表达式为

(24)

考虑到约束(13)，式(24)的分母项(定义为den)可以转化为

(25)

其中：

(26)

定义推力积分系数为

(27)

(28)

有

(29)

(30)

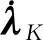
对于积分

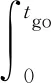
(31)

做变换

(32)

于是积分可以转化为

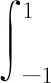
(33)

其中：

(34)

根据GLQF可得积分式(33)的值为

(35)

式中：si为高斯-勒让德求积公式的节点；Ai为相应的系数。同理令

(36)

可以得到

(37)

对于二重积分

(38)

做变换

(39)

Jacobi行列式为

(40)

于是积分式(38)可以转化为

(41)

其中

gS(α,β)=

(42)

积分式(41)的值为

(43)

同理令

gQ(α,β)=

(44)

可以得到

(45)

GLQF方法精度取决于节点个数。

图2 推力积分对比图Fig.2 Comparison chart of thrust integral

3 迭代过程中引力积分计算

文献[12]基于平均引力场假设进行引力积分运算，在发动机故障导致的小推力长燃弧情况下计算精度较差。本文采用球极坐标系下泰勒多项式逼近的方式给出了一种适用于小推力长燃弧飞行模式的引力积分近似解[8]：

定义引力积分为

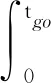
(46)

(47)

定义平均位置rv和rr，满足：

(48)

(49)

在线性引力场假设下，得到rv和rr的近似表达式

(50)

(51)

在球极坐标系下估算平均位置更适用于小推力长燃弧模式。令vd为满足终端约束的目标入轨点速度，rd为目标入轨点位置，建立如图3所示的球极坐标系。图3中erdy为沿rd的单位矢量，er0y为沿r0的单位矢量，erdz为沿入轨点坐标系OZ轴的单位矢量，有

erdx=erdy×erdz

(52)

图3 球极坐标系示意图Fig.3 Diagram of polar coordinate system

er0x=er0y×er0z

(53)

er0z=er0x×er0y

(54)

令r0的极坐标形式为

(55)

其中旋转角为

ψ0=arcsin(er0y·er0z)

(56)

由于ψ0通常是一小量，所以可以近似得到

φ0=arcsin(er0y·er0x)

(57)

同理可以得到rd的极坐标形式

(58)

以及它们对时间的一阶导数

(59)

(60)

由泰勒展开式可知任意时刻的位置矢量r(t)的极坐标形式为

(61)

其对时间一阶导数为

(62)

令平均位置rv和rr的极坐标形式分别为pv和pr，其近似值取做

(63)

(64)

结合式(61)计算得到

(65)

把pv和pr转换到入轨点坐标系下，得到

rv= [cospv2(erdycospv3+erdxcospv3)+

erdzsinpv2]pv1

(66)

rr= [cospr2(erdycospr3+erdxcospr3)+

erdzsinpr2]pr1

(67)

式中：pr1表示pr的第1个坐标，其余同理。最终由式(48)和式(49)计算出引力积分值。

4 迭代制导计算流程

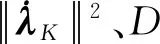
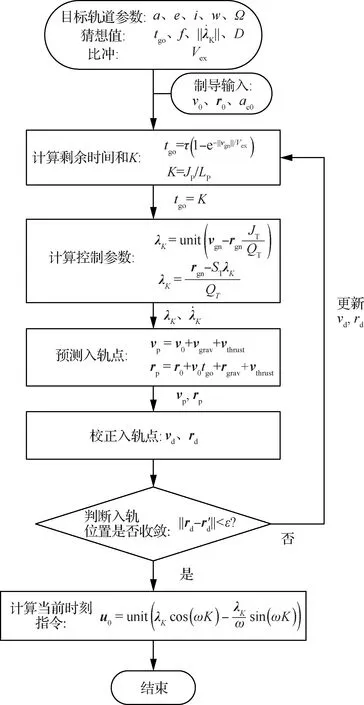
图4 制导算法流程图Fig.4 Flow chart of guidance algorithm

4.1 计算剩余时间tgo和K

定义剩余速度vgn和剩余位置rgn

vgn≡vd-v0-vgrav

(68)

rgn≡rd-r0-rgrav-vtgo

(69)

对式(1)前两式进行两次积分，可以看出

(70)

即

(71)

(72)

对推力积分进行简化，认为ω(t-K)为小量，并假设[8]

(73)

对式(27)进行泰勒展开并忽略二阶小量，得到

(74)

其中：LP和JP是近似的推力积分系数，仅应用于本环节，其表达式为

(75)

将式(74)代入到式(71)中，得到

(76)

令

(77)

从而得到

JT≈0

(78)

因此有

(79)

所以剩余时间为

(80)

根据式(68)和式(80)，可以迭代求出剩余时间tgo的值，而K的值依然由式(77)决定。

4.2 计算控制变量λK和

由4.1节求出tgo和K后，根据第2节中式(35)、式(37)、式(43)和式(45)可以计算出推力积分系数LT、JT、ST、QT，由式(71)～式(72)可以得到

(81)

(82)

其中：

A=ωsin[ω(tgo-K)]vd-

(83)

B=cos[ω(tgo-K)]vd+

(84)

在式(72)两端同时点乘B，结合式(82)可以得到修正后的ST表达式

(85)

最终得到

(86)

在式(10)中令ω趋于0，得到控制矢量的近似表达式为

(87)

图5 控制量限幅和入轨点校正示意图Fig.5 Diagram of control limits and injection point correction

首先计算出当前时刻单位推力矢量

(88)

当erdx·u0≥0时，不需要做任何调整，否则令

erdx·u0=0

(89)

(90)

4.4 入轨点预测和校正

根据式(29)和式(30)计算得到推力积分vthrust和rthrust，则预测入轨速度vp和位置rp为

(91)

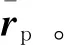
令rd与入轨点坐标系的Y轴的夹角为θ，其表达式为

(92)

参考入轨点的真近点角为f*，则目标入轨点的真近点角为

fd=f*+θ

(93)

可以得到rd的模值为

(94)

于是

(95)

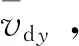
(96)

于是

(97)

当校正后入轨点位置收敛时，认为本周期迭代制导算法收敛，当前时刻制导指令由式(88)给出。

5 仿真验证

为了验证本文所改进迭代制导方法的最优性、发动机故障状态下算法适应能力以及各种干扰条件下算法的鲁棒性，本文针对某型火箭大气层外末级入轨飞行段进行迭代制导算法评估。

5.1 仿真初始和终端条件

火箭初始质量为184 334.0 kg，发动机参数轴向推力为999 036 N，秒流量为56.029 kg/s。初始点和标准入轨点轨道要素见表1。

表1 仿真初始点和标准入轨点轨道根数

5.2 干扰条件下制导算法鲁棒性验证

为了验证本文所改进的迭代制导算法的鲁棒性和入轨精度，针对火箭末级给出的各种干扰和偏差(如表2所示)，进行了1 000次蒙特卡罗打靶仿真，打靶结果见图6、表3和表4。

从蒙特卡罗打靶统计结果中可以看出，在表3 所示的偏差条件下，采用本文方法可以使火箭满足5个终端约束精确入轨且迭代步数不大于5，说明算法可以同时适应多种偏差，具有较强的收敛性和鲁棒性。

表2 蒙特卡罗打靶偏差项设置Table 2 Setting of error terms in Monte Carlo simulation

5.3 发动机故障情况下制导算法适应性验证

由于本文只对发动机出现非灾难故障状态时(包括燃料堵塞、燃料泄漏、燃烧室压强异常、伺服机构卡死等状况，但总冲依然满足入轨要求)验证制导算法适应能力，此时发动机故障对制导的影响可归结为秒流量大幅下降和等效比冲下降，因此设计了表5所示的3种典型故障模式。其中，当等效比冲与预装订值一致时可以通过实时测量视加速度获取秒流量变化，因此故障模式1主要验证当故障精确已知模式下算法的最优性；而某些特殊发动机故障模式会导致秒流量和等效比冲同时出现大幅下降，这对算法鲁棒性和适应性同时提出挑战，表5中的故障模式2和故障模式3对该模式下算法性能进行验证。

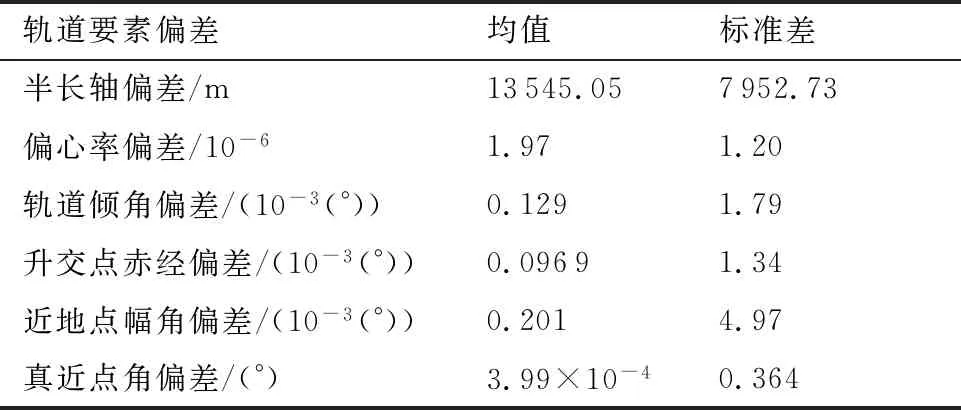
表3 蒙特卡罗仿真结果Table 3 Results of Monte Carlo simulation

表4 最大迭代步数统计Table 4 Statistics of maximum iteration steps

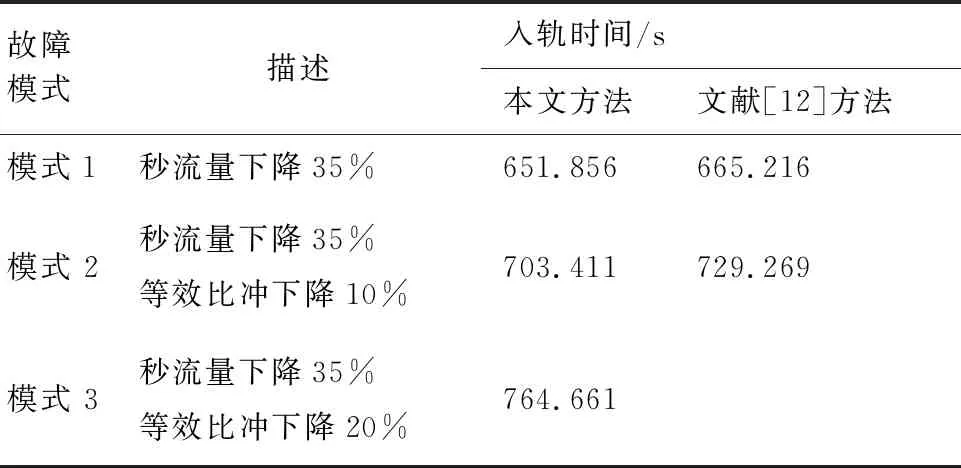
表5 不同故障模式下入轨时间统计Table 5 Entry time in different fault modes

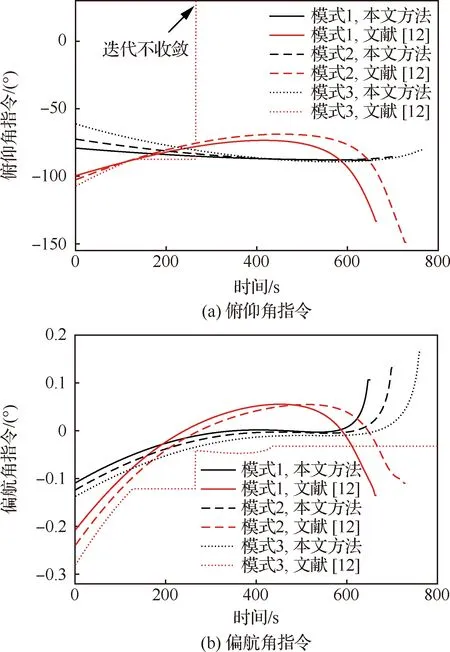
图7 推力故障情况下制导指令对比Fig.7 Comparison of guidance instructions with thrust fault

采用本文算法与文献[12]中的迭代制导算法进行仿真对比，仿真结果见表4～表5和图7～图8。仿真结果显示，本文改进的制导算法在模式1条件下相对于文献[12]方法关机时间提前了约13.36 s，说明本文采用的包括改进推力积分和引力积分等措施可以提高算法最优性；在模式2和模式3条件下，随着等效比冲的下降幅度增大，文献[12]方法会出现迭代不收敛的状况，而本文方法依然可以保障火箭精确入轨。此外，从表4中可以看出故障模式2下本文方法相对于文献[12]方法将关机时间提前了约25.86 s，说明在更严重的故障状况下本文方法最优性也更明显。

为进一步获得2种方法对故障的适应边界，本文将秒流量下降幅度设置为额定的35%，文献[12]方法最多可以适应16%的等效比冲下降，而本文改进的制导方法可以适应25%的等效比冲下降，进一步验证了本文所提方法对故障具有更强的鲁棒性和适应性。

图8 推力大偏差情况下轨道根数曲线对比Fig.8 Comparison of orbital elements curves with thrust fault

由于算法采用预装订的迭代初值，在故障发生之后的第一个制导周期内收敛时间最长，因此在故障模式2的第一个制导周期将本文方法与文献[12] 方法就算法收敛过程进行对比，结果如图9 所示。其中niter表示迭代步数，xmiss表示本步与上一步迭代的目标入轨位置X坐标之差的绝对值。结果说明在故障模式下本文方法收敛速度更快。

表6显示在不同故障模式下对于任意给定的真近点角初值，算法均能在有限步数内收敛(表6中边界模式指秒流量下降35%，比冲下降25%的算法适应边界状况)，说明算法对于初值不敏感并且可以保障实时性。

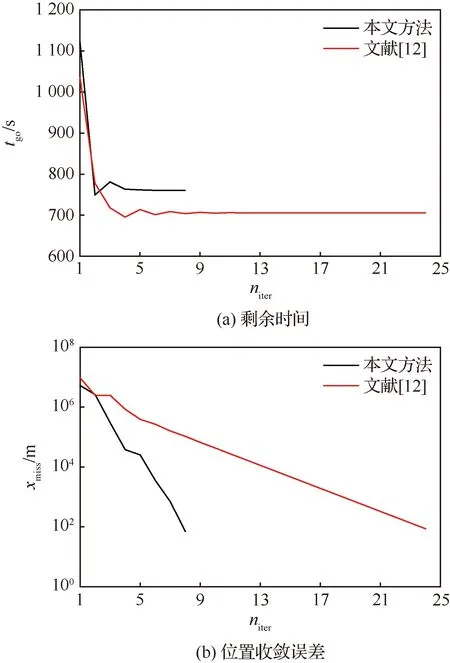
图9 故障模式2下收敛过程曲线对比Fig.9 Comparison of convergence curves in fault mode 2

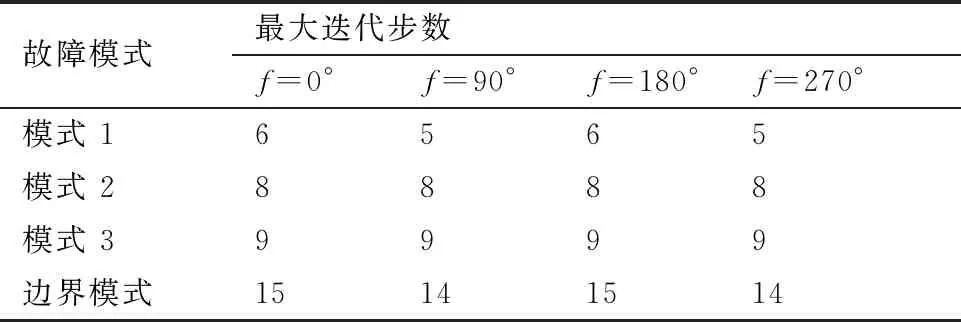
表6 不同故障模式下最大迭代步数统计Table 6 Maximum iteration steps in different fault modes

6 结论

1) 本文基于文献[12]与PEG方法，重新推导了满足5个轨道根数约束的准确的横截条件，采用了精度更高的推力和引力积分方法，因此进一步完善了算法流程，具有较强的最优性和适应性。

2) 本文方法相对于文献[12]方法在相同推力故障情况下具有更强的最优性与收敛性，且对于更严重的推力故障鲁棒性和适应性更强。

3) 本文对多变量参数最优化问题进行降维迭代求解，并结合控制量限幅算法，保障了故障条件下算法的收敛性与实时性，且能适应多种偏差，具有一定的工程实用价值。

[21] AHMAD N, HAWKINS M, VON DERPORTEN P, et al. Closed loop guidance trade study for Space Launch System Block-1B vehicle[C]∥41st AAS GNC Conference, 2018.

附录A:

由于开普勒轨道满足:

(A1)

式中：vf和rf分别为vf和rf的模值，上标*表示轨道根数的目标值。所以半长轴约束为

(A2)

由于轨道角动量模值h满足:

h2=μ·p=μ·a*(1-e*2)

(A3)

式中：p为轨道半通径，所以式(A2)和式(A4)共同约束了目标轨道偏心率大小。

C2=(rf×vf)·(rf×vf)-μ·a*(1-e*2)=0

(A4)

令N表示轨道平面与赤道平面交线(由地心指向升交点)单位矢量，则近地点幅角的表达式为