基于双向电机驱动的四旋翼机动飞行控制
2021-03-26徐力昊张宇许斌
徐力昊,张宇,*,许斌
(1.浙江大学 控制科学与工程学院 工业控制技术国家重点实验室,杭州310027;2.西北工业大学 自动化学院,西安710072)
以四旋翼飞行器(QUAV)为代表的多旋翼飞行器由于其机械结构简单、动力学易于分析的特点,被广泛研究。但是四旋翼是典型的欠驱动系统,机动性能较为欠缺。因此,如何提高四旋翼的机动性是研究领域的一大挑战,也是提升其应用范围的重要研究热点。
四旋翼的动力组件主要由电机、电子调速器(简称电调)与桨叶组成。在飞行过程中,电调驱动带桨叶的电机,通过调节转速以改变推力。传统的四旋翼始终是由单向电流驱动桨叶逆时针或顺时针单向转动,推力变化率较小,这是制约四旋翼整体动态特性提高的原因之一。
造成上述问题的软硬件因素有:①电调信号是单向的,通过预设的编程,调制方式主要是单极性的PWM 波形调制,导致输出电流只能改变大小而不能改变方向;②桨叶是非对称单向桨叶,在单向旋转时效率较高,但是反转则不能或产生很小的推力。
为了克服上述缺陷,有研究使用传统电调加可变桨距[1-4]的桨叶组合,实现了电调驱动电机单向旋转,同时可以产生双向推力,但是该方案增加了复杂的变桨距结构,且需要额外的桨距控制器,增加了整体的机械结构质量。因此,变桨距四旋翼负载能力更弱,续航时间更短。
也有研究通过增加控制输入使四旋翼从欠驱动改进为过驱动[5-7]。实现方法是增加倾斜的旋翼推力系统,即改变了欠驱动特性,也能有效抵抗扰动,但由于倾斜角度是有限的(小于90°),改善动态特性的输入范围也是有限的。
虽然已有研究提出使用双向电调产生双向电流驱动电机在飞行中双向旋转[8-12],完成了翻转之后悬停等之前不能实现的机动动作,但是没有分析双向电流对改善控制的动态特性,特别是姿态角跟踪的优势,也没有对从双向转速到力矩和推力的控制分配矩阵进行讨论。
分析已有方案的优缺点,本文结合四旋翼动力学特点,实现了一种四旋翼,其电调使用双极性PWM调制,使得在飞行过程中可以驱动电机快速减速或者改变旋转方向。桨叶使用对称桨叶,正反转都有足够升力。具有双向推力的四旋翼创新之处在于:可以提高姿态和位置跟踪的机动性,也可以在倒置状态下(θ=π)悬停或实现机动动作。例如,可通过增加正压力停靠在倾斜表面,抵抗来自不同方向的外力等。本文推导了该四旋翼翻转动作的动力学过程,提出了一种适用于双向转速的迭代控制分配方法来控制双向的推力与转矩,并通过平面轨迹规划与四旋翼模型仿真证明了本文方法的有效性。
1 四旋翼建模与运动姿态分析
1.1 动力学模型
刚体四旋翼的重心动力学模型[8]如下:
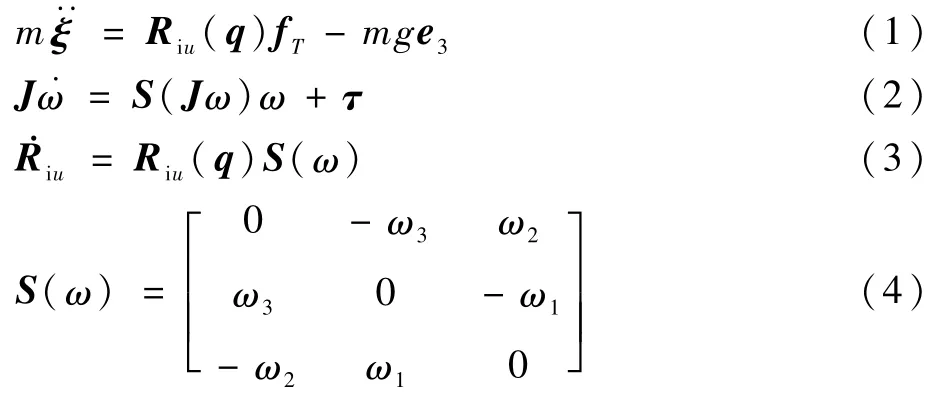
式中:ξ为重心的位置;ω为机体角速度;m为机体质量;J为转动惯量;g为重力加速度;fT为机体坐标系中的总推力;τ为机体的总转矩;e3=(0 0 1)T为单位向量;Riu(q)为惯性坐标系中四旋翼的方向,使用四元数q=(qwqxqyqz)T表示避免奇点;S(ω)为斜对称矩阵,代表叉乘。使用哥氏定理可以推导得到旋转矩阵的微分方程(3)。
1.2 正反状态转换的过程
分析等式(1)可以得到正向悬停状态与翻转后悬停状态的不同等式,可以作为新型四旋翼从普通状态到特殊状态的比较。
对于本问题中设定的任意偏航角,始末状态在同一个平面内翻转(开始θ=0,结束θ=π)。
翻转前:
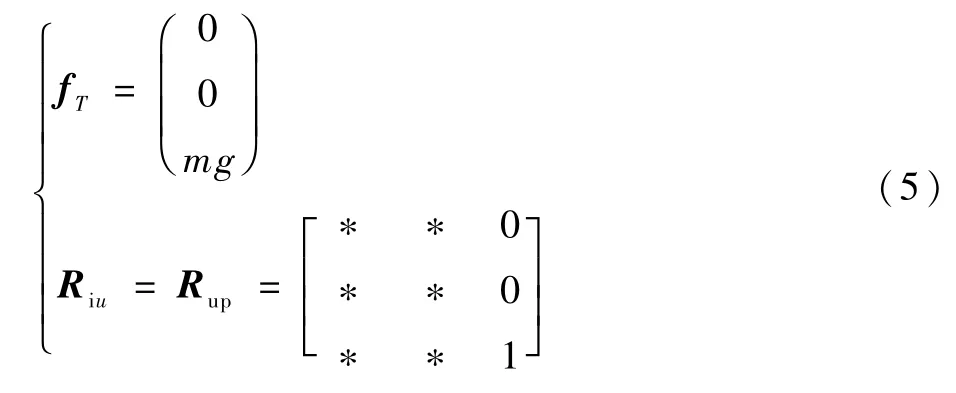
式中:Rup为四旋翼机体坐标系z轴竖直向上状态时的Riu;“*”为无关元素,为了保证平衡,r1,3、r2,3都是0。
翻转后,四旋翼产生机体坐标系中的反向推力,所以可以保持倒转悬停姿态。
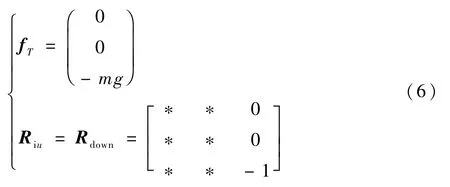
式中:Rdown为四旋翼机体坐标系z轴竖直向下状态时的Riu。
在翻转过程中,运用矩阵形式的欧拉-罗德里亚斯公式[9](7)表示翻转矩阵Rflip:
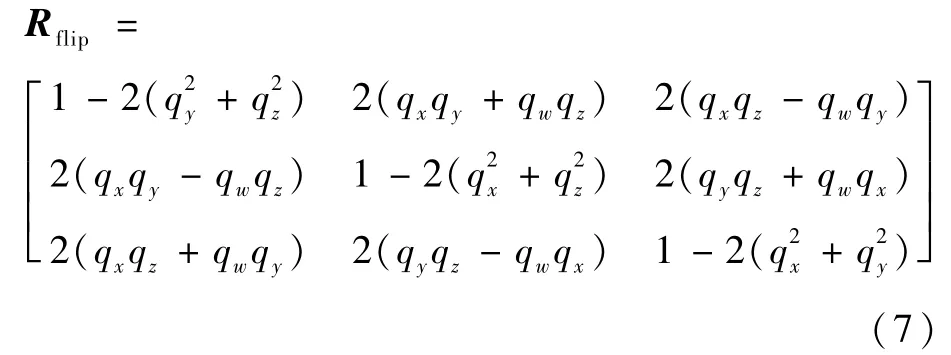
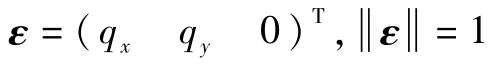
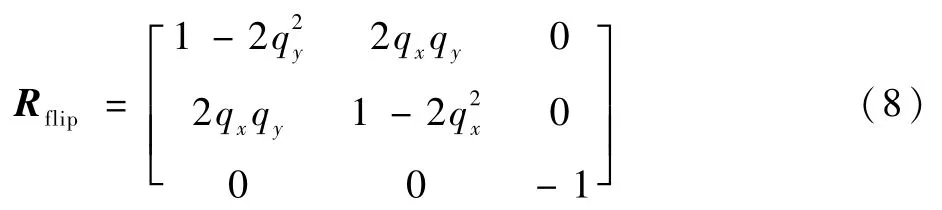
翻转前后重心位置可能改变,3个转动惯量中只有Ix、Iy增加,3个转矩均不变,适用于新型四旋翼的翻转等轨迹设计将在4.1节使用最优规划方法实现。
2 控制器设计与转矩分析
2.1 姿态与位置控制
四旋翼的位置与姿态控制常使用串级PID控制器实现,即位置控制器的输出指令传递给姿态控制器。由于四旋翼具备微分平坦性[7]的特点,控制器输入fT、τ可以直接由目标位置ξ得到,而且第4节的平面轨迹规划也需要得到控制输入fT、τ,但是为了第4节的四旋翼模型仿真,即使没有位置控制器也可以实现姿态控制,本节仍然采用串级PID控制器作为理论基础。
跟踪期望位置ξd=(xdydzd)T的控制器等式如下:
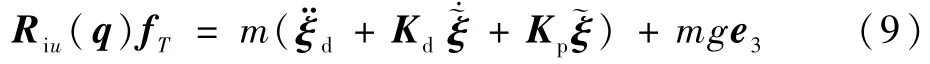
式中:Kd∈R3×3为微分系数对角 矩阵;Kp∈R3×3为比例系数对角矩阵;~ξ=ξd-ξ为位置误差。
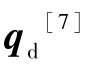
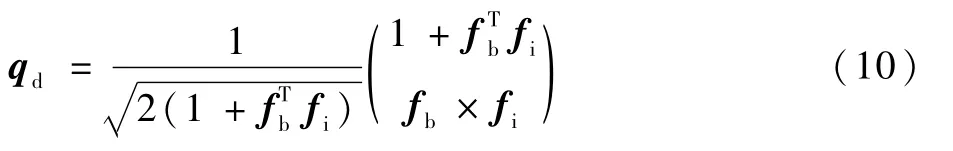
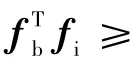
使用上文提到的欧拉-罗德里亚斯公式得到R(qd),再得到旋转矩阵Rid=RswitchR(qd)(四旋翼机体坐标系z轴竖直向上状态时Rswitch=I3×3,四旋翼机体坐标系z轴竖直向下状态时Rswitch=Rflip),将旋转矩阵输入姿态控制器[7]:
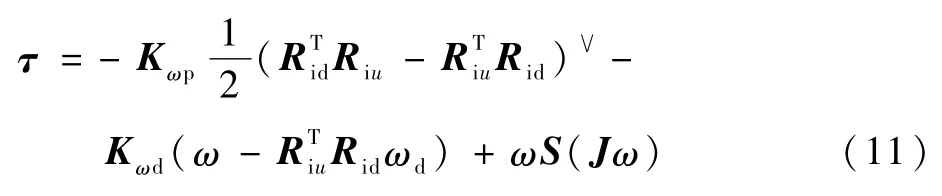
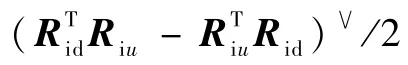
2.2 转矩设计
使用双向的旋转桨叶可以产生垂直于电机中轴线的正反推力,增加最大转矩,提高姿态角变化的动态特性。推力与转速、转矩与转速的映射关系如下[8]:
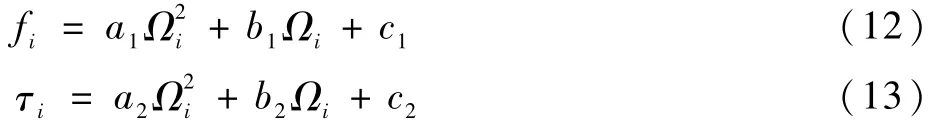
式中:a、b、c分别为二次、一次、零次项的系数;Ωi、fi、τi(i=1,2,3,4)分别为电机的转速、推力、转矩。
推力向量为

式中:ni为垂直于电机平面的单位向量。
机体坐标系重心到电机中心的坐标变换如图1所示。式中:l为机体重心到电机的机臂长度。
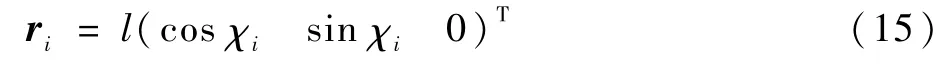
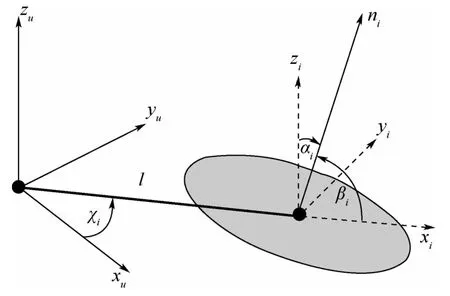
图1 机体坐标系重心到电机中心的坐标变换Fig.1 Coordinate transformation from the center of gravity axis to the center of motor axis
从惯性坐标系到电机的单位向量转换公式为
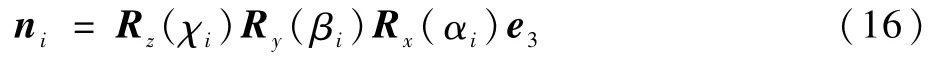
则每个电机上的转矩为

式中:第1项为俯仰滚转转矩,转矩方向由ri代表的推力方向确定;第2项为垂直于ni平面的偏航转矩;Pi∈{-1,1},1为顺时针,-1为逆时针,这一项的正负由电机转向方向确定。
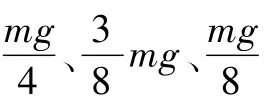
1)稳定姿态
绕机体中心轴的转矩(2CW++)=(2CC++)机体平衡,如图2所示。
2)俯仰与滚转(以滚转为例)
①原始俯仰滚转(见图3(a)):绕机体中心轴的转矩(CW+++)+(CW+)=(CC+++)+(CC+),机体绕z轴的方向平衡(式(17)中转矩公式第2项为0),第1项不平衡,机体做滚转运动。
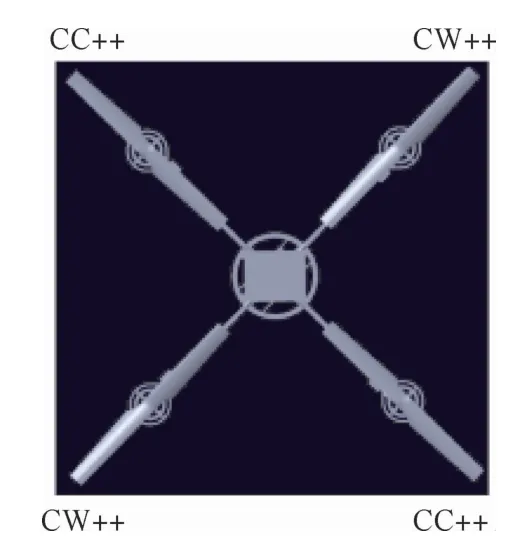
图2 稳定姿态的推力Fig.2 Thrust graph under stable attitude
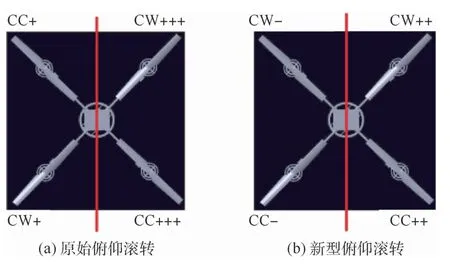
图3 滚转的推力Fig.3 Thrust graph of roll
②新型俯仰滚转(见图3(b)):绕机体中心轴的转矩(CC+)+(CC++)=(CW+)+(CW++),机体绕z轴方向平衡(式(17)中转矩公式第2项为0),第1项不平衡,机体做快速的滚转运动。
3)偏航
①原始偏航(见图4(a)):绕机体中心轴的转矩(CC+++)+(CC+++)>(CW +)+(CW+),机体绕z轴方向不平衡(式(17)中转矩公式第2项,机体逆时针旋转),第1项平衡。
②新型偏航(见图4(b)):绕机体中心轴的转矩(CC+++)+(CC+)+(CC+++)+(CC+),机体绕z轴方向不平衡(见式(17)中转矩公式第2项,机体逆时针快速偏航旋转),第1项平衡。
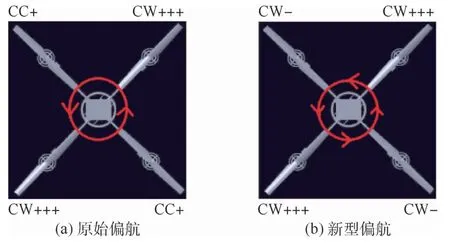
图4 偏航的推力Fig.4 Thrust graph of yaw
3 控制分配矩阵设计
本节讨论通过第2节得到的推力与转矩向电机转速的映射,即控制分配的过程。
将式(17)写为矩阵形式,即
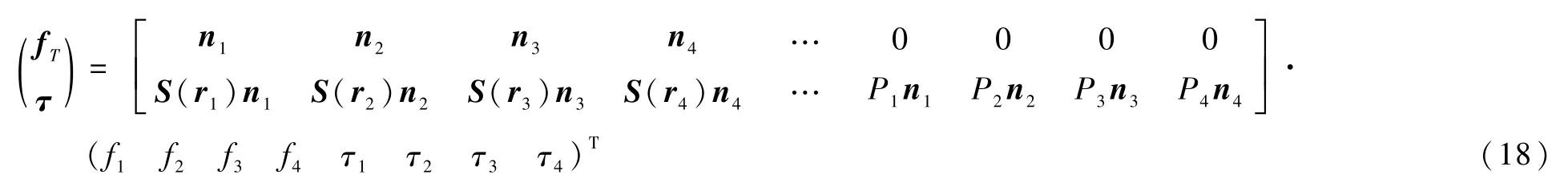
位置和姿态控制器给出期望的fT和τ指令,需要求解出每个电机的转速,为了得到新的Ωi,通过已测量得到的当前Ωi0与目标推力数值fi、转矩数值τi的关系,使用常用的线性化方法。
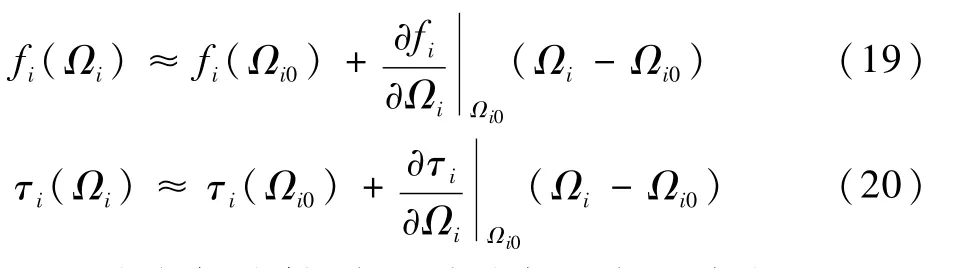
为方便映射,定义分块斜对角矩阵为
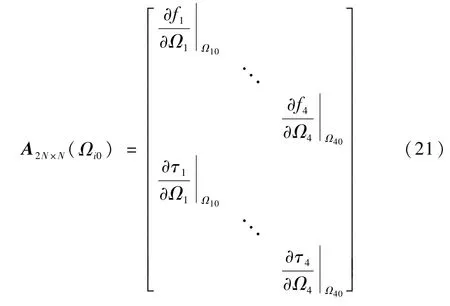
对应于式(19)、式(20)的矩阵:
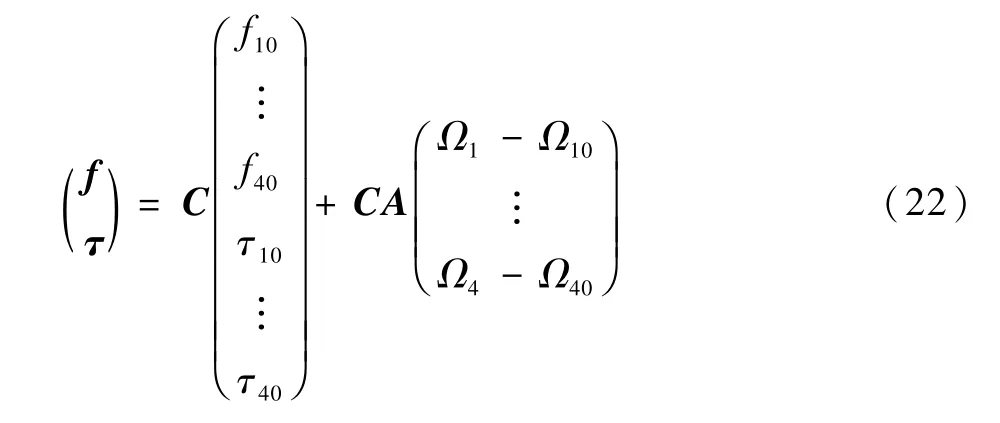
类似于(f τ)T=B(Ω21… Ω2N)T的控制分配矩阵为B=CA,将需要计算求得的各个电机转速写到等式左侧:
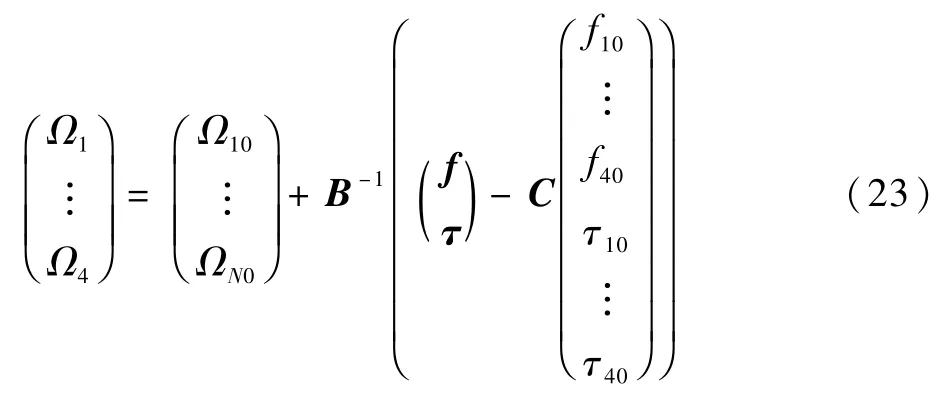
在实际使用中,通过电调测量得到Ωi0,计算得到fi0、τi0,使用式(19)~式(23)得到现在时刻的fi、τi。
分析已有的控制分配矩阵:
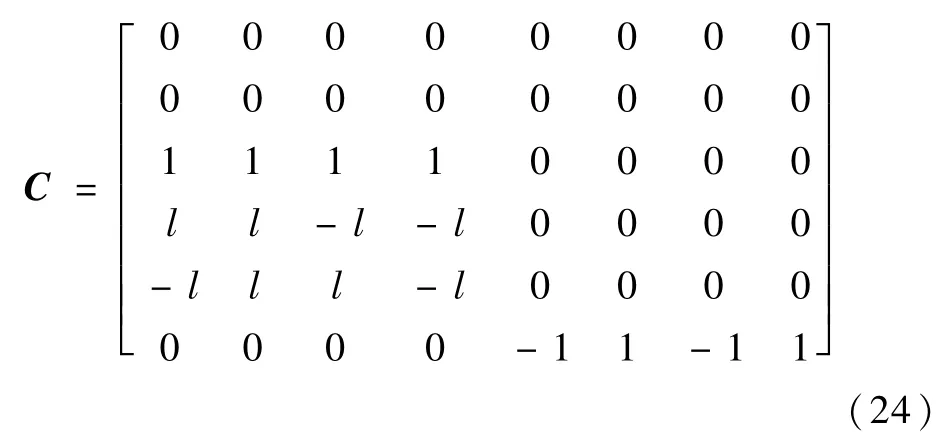
矩阵(24)表示电机编号顺序与转向,可见偏航与滚转俯仰相互独立,所以可以把C矩阵中的3个分块(推力、俯仰滚转、偏航)组合在一个矩阵中:式中:从转速到推力和转矩的恒定映射分别表示为cf、cτ。
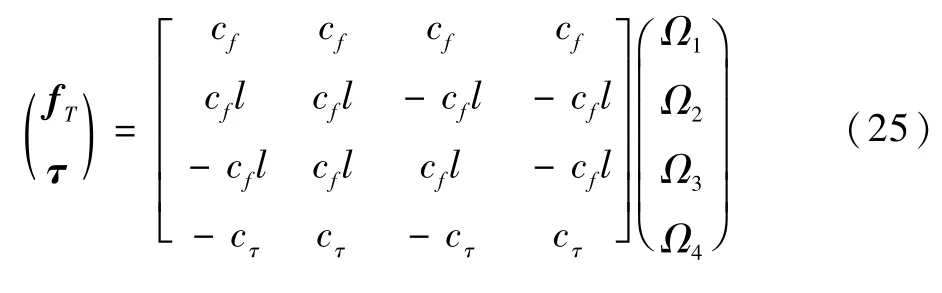
由图3分析可见,新型四旋翼滚转俯仰时,即使是同奇偶性的电机也会有不同的转向,所以设置Oi∈{-1,1}为1、3号电机推力与转矩的方向符号,1为顺时针,-1为逆时针。设置Ei∈{-1,1}为2、4号电机推力与转矩的方向符号,1为逆时针,-1为顺时针。
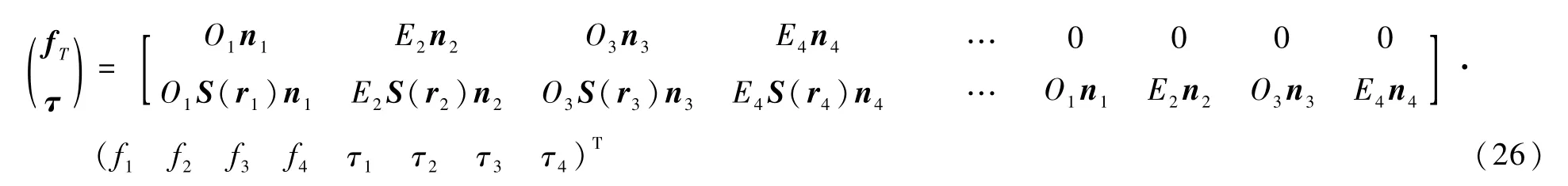
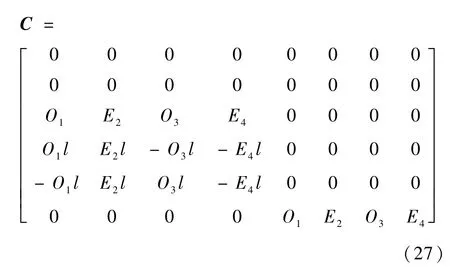
将矩阵(27)转化为矩阵(25)的形式:
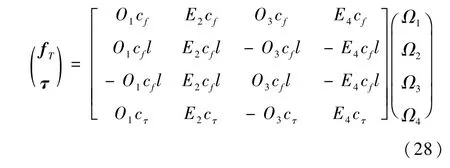

4 试验设置与结果分析
4.1 x-z平面轨迹规划试验
基于前文设计的新型四旋翼动力学与控制分配方法,为了规划适用于新动力学和类似于翻转新任务的轨迹,先考虑计算量和限制较少,以及xz平面内的各种轨迹设计(二维平面内的轨迹),所以使用x-z平面四旋翼模型[9,13],如图5所示。
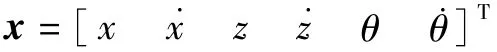
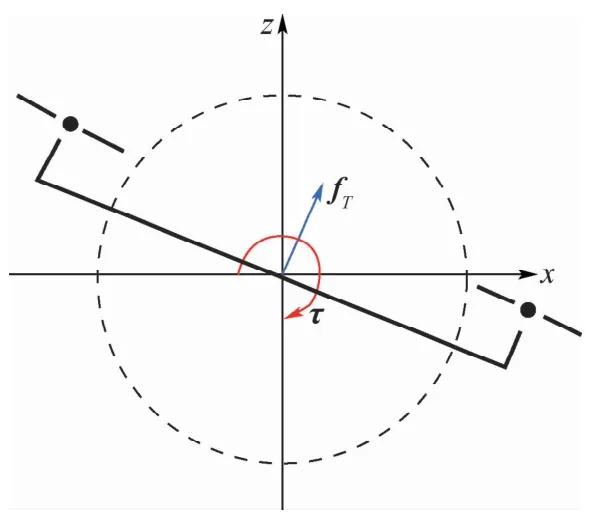
图5 x-z平面四旋翼模型Fig.5 Model of x-z plane quadrotor

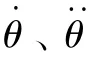
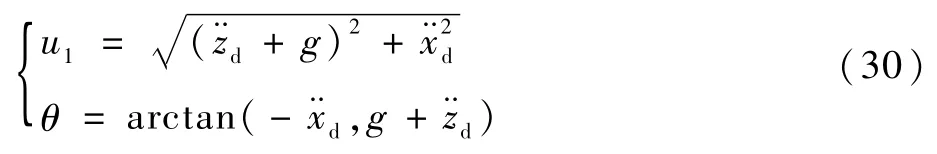
接下来基于提出的平面模型考虑搭建最优控制问题来计算运动轨迹。
首先定义控制量u*,使得

式中:x∈Rn;u∈Rm;t∈[t0,tf],满足路径限制及边界条件:
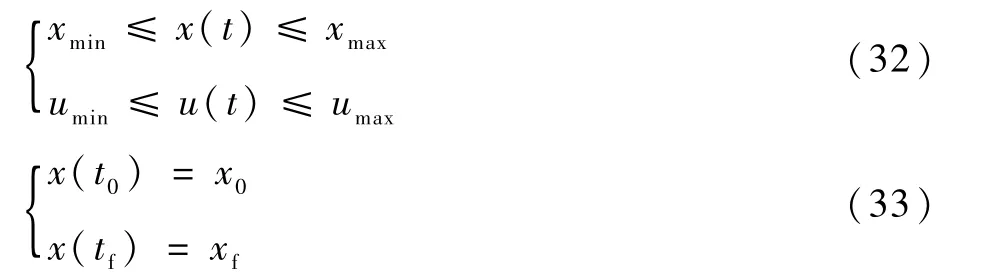
跟踪路径x*,该路径最小化了[14]:
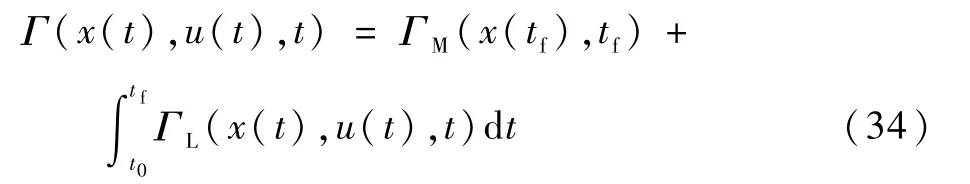
更新平面模型:
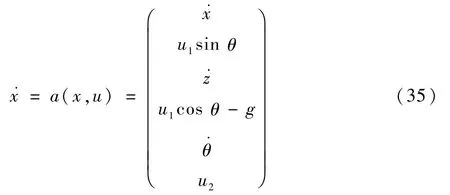
式(35)中,输入控制u=[u1u2]T的限制为

表1展示了本文设置的参数与限制。
使用基于高斯伪谱法的MATLAB GPOPS工具箱[15],利用数值方法求解这个最优控制问题。考虑最小时间问题,所以设置ΓM=tf,ΓL=0。
使用MATLAB GPOPS工具箱可以定义具有状态约束和输入约束的任意机动或者是解决多阶段问题,每个机动阶段都能包含过程中的任何可行状态,如在阶段边界处定义速度和俯仰角。系统参数与状态、输入限制如表1所示。
为了试验翻转的可行性,测试如下3种典型机动:点到点、点到竖直悬停、翻转,为新型四旋翼的新应用场景做理论准备,如利用反向推力紧贴垂直或者大倾角墙壁等。每个机动可能包括多个阶段,所以需要考虑每2个阶段之间的连接条件。表2展示了这3个机动的设计。

表1 系统参数与状态、输入限制Table 1 System parameters,status and input limits

表2 三个典型机动设计Table 2 Design of three typical maneuvers
1)点到点:规划目标是最小时间到达预计点pf=[xgzg0]T,到达时速度为0。
2)点到竖直:点到竖直是一种特殊的点到点机动,最终姿态角不为零(θ=π/2),规划目标是最小时间到达预计点pf=[xgzgπ/2]T。该设置证明了四旋翼可以在特定的时间点保持非稳态的姿态角。
3)翻转:在机动过程中,四旋翼通过特殊的中间过程点pmid=[xmidzmidπ/2]T。最后实现与起始点位置相同且翻转:pf=[xg0 π]T,最终速度也为0,该设置验证了新任务场景下的实现可行性。
3组试验结果分别展示了θ(见图6(a)、图7(a)、图8(a))、输入u1(见图6(b)、图7(b)、图8(b))和u2(见图6(c)、图7(c)、图8(c))的变化,以及飞行轨迹(见图6(d)、图7(d)、图8(d)),其中箭头在机体中央竖直向上,表示机体的姿态角,实线代表0<θ≤π/2,虚线代表π/2<θ<π。
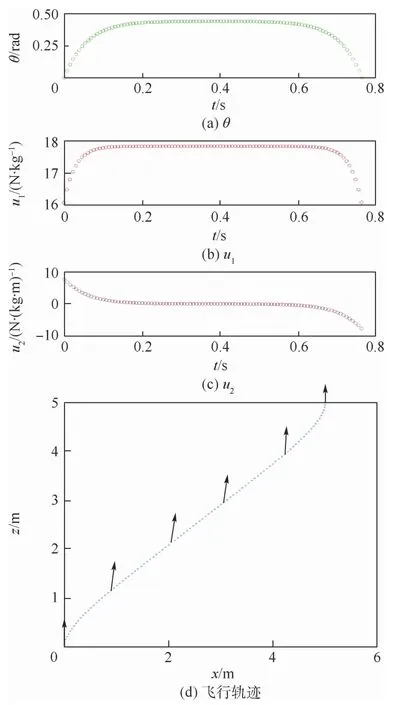
图6 点到点的θ、u1、u2 及飞行轨迹Fig.6 Trajectory graph of point-to-point with θ,u1,u2
试验结果显示,使用MATLAB GPOPS工具箱轨迹规划方法和设计约束条件,新型四旋翼可以使用连续的双向推力与转矩,实现快速机动与翻转后的悬停,本文试验结果可能不是时间最优或推力最优,是因为设置的约束和运动阶段可能不是在当前的最优。例如,试验中翻转的飞行轨迹在0<θ≤π/2和π/2<θ<π这2个阶段并不对称,如果设置更多约束和更多运动阶段,可能会有不同的结果。
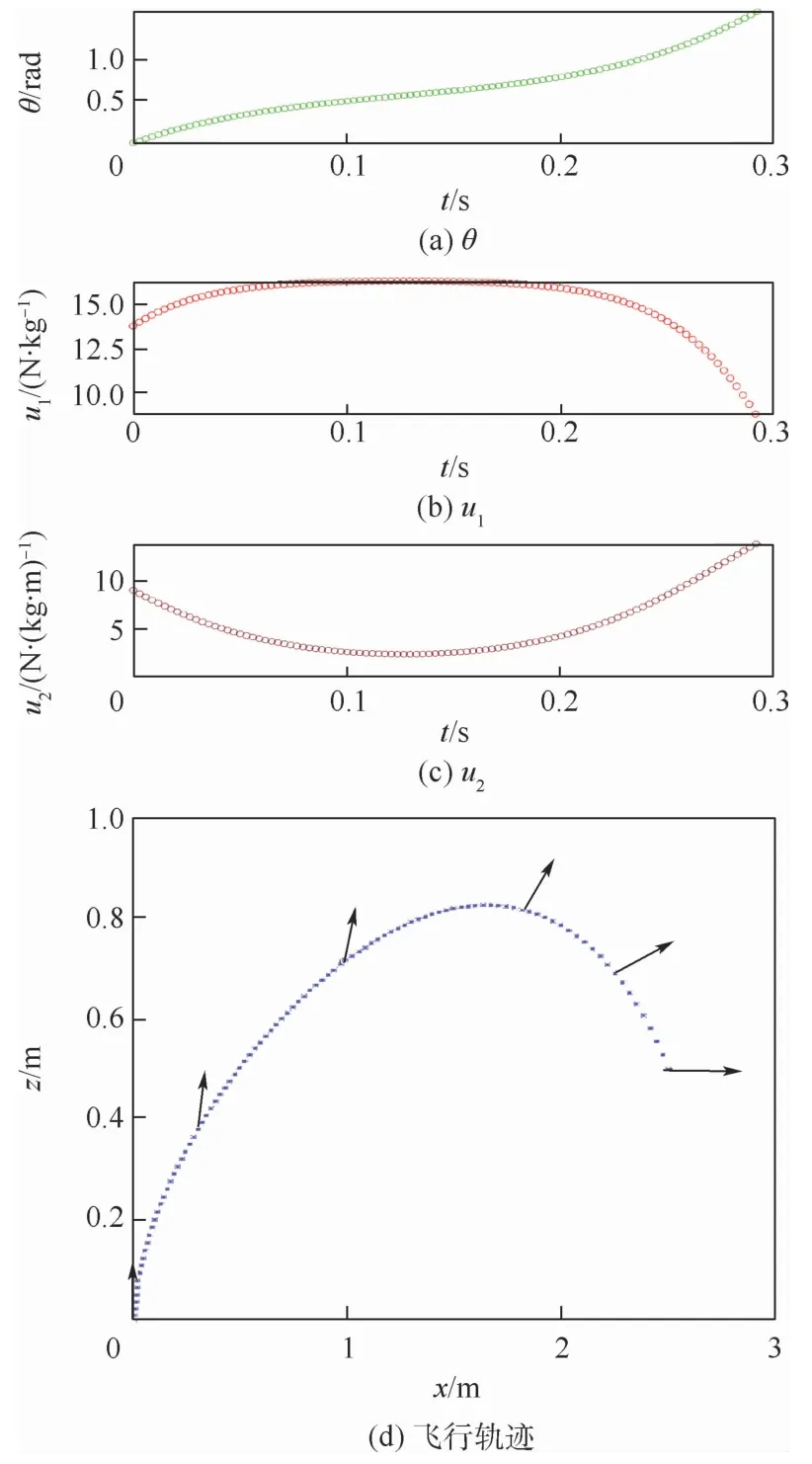
图7 点到竖直悬停的θ、u1、u2 及飞行轨迹Fig.7 Trajectory graph of point-vertical hover with θ,u1,u2
4.2 四旋翼模型仿真
搭建四旋翼模型作为被控对象,包括实际尺寸网格模型、质量、转动惯量等实际物理量,建模使用基于真实四旋翼模型部件组装的仿真模型,质量均匀分布于器件,负载4个集成了新型电调的双向直流无刷电机作为执行器。电机转子转动惯量、绕线组电阻、反电动势系数等参数参照实际设置。可以实现双向电流驱动电机双向旋转与反向电流减速。
姿态(φ,θ,ψ)和位置(x-y-z)控制器分别采用串级PID控制器,设置3个试验:姿态角(以滚转为例)跟踪(见图9)、高度跟踪(见图10)、螺旋曲线轨迹跟踪(见图11),其中控制器的控制参数Kd、Kp、Kωd、Kωp等使用Simulink的PIDTuner工具辨识系统后得到,为了保证单向与双向电流驱动结果的对照性,试验中参数设置均相同。
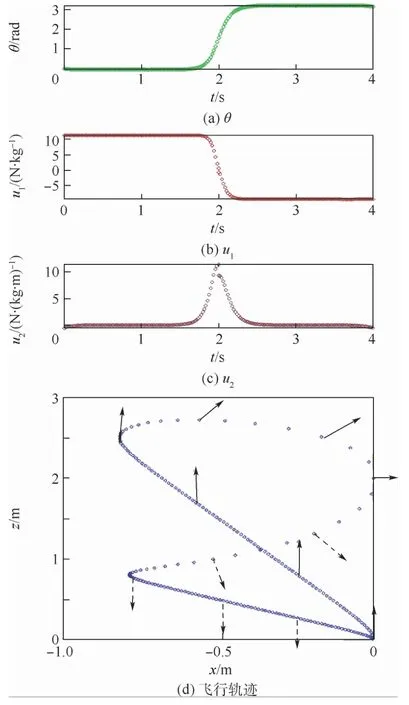
图8 翻转的θ、u1、u2 及飞行轨迹Fig.8 Trajectory graph of flip with θ,u1,u2
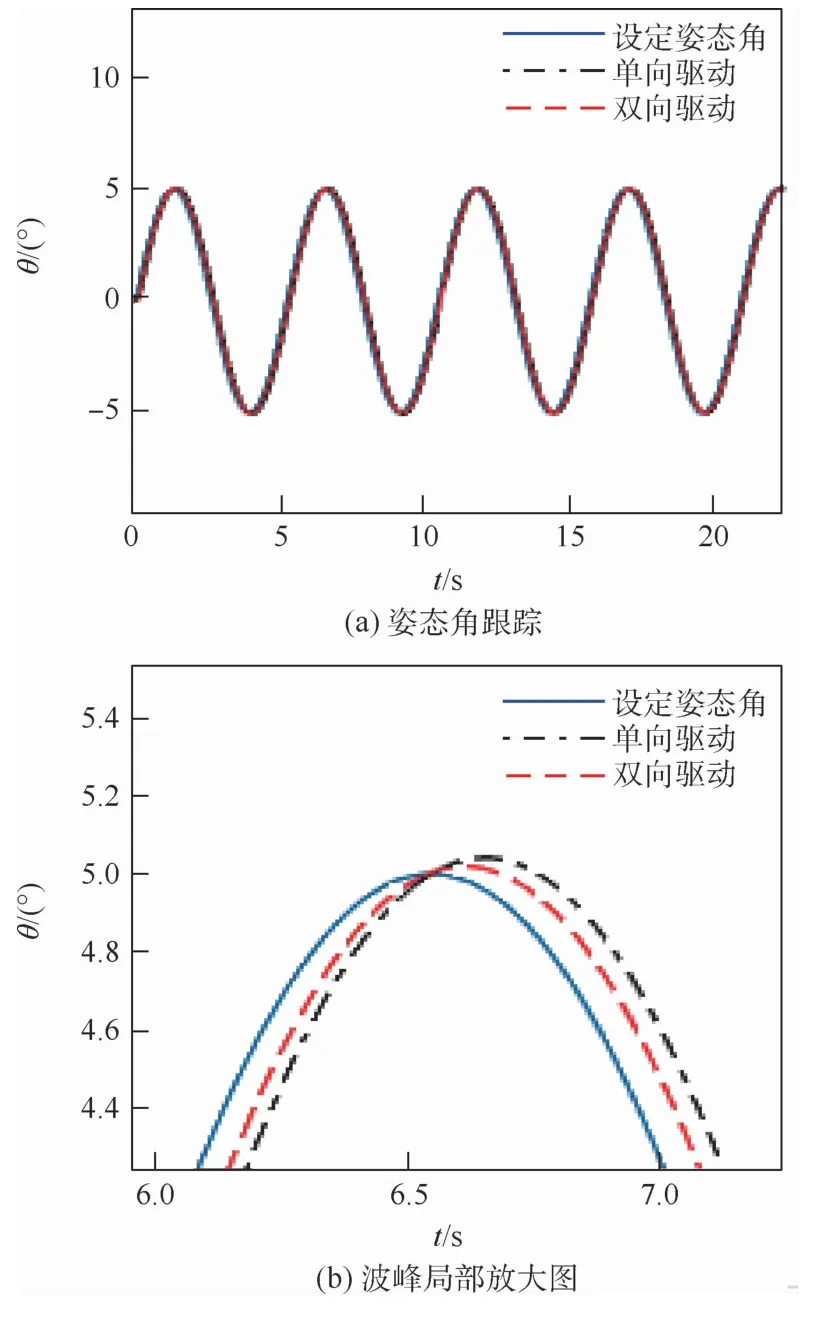
图9 姿态角跟踪结果Fig.9 Attitude angle tracking results
姿态角跟踪与高度跟踪试验显示,双向电机驱动的四旋翼对比传统四旋翼的主要优势在于:可以实现电机快速减速,减少超调量,尤其是在高速机动的条件下,但是在加速阶段,2种四旋翼的性能差别较小。跟踪螺旋曲线试验(见图11与表3)也显示了双向电机驱动的四旋翼可以改善欠驱动系统机动性差的缺陷,提升轨迹跟踪精度。
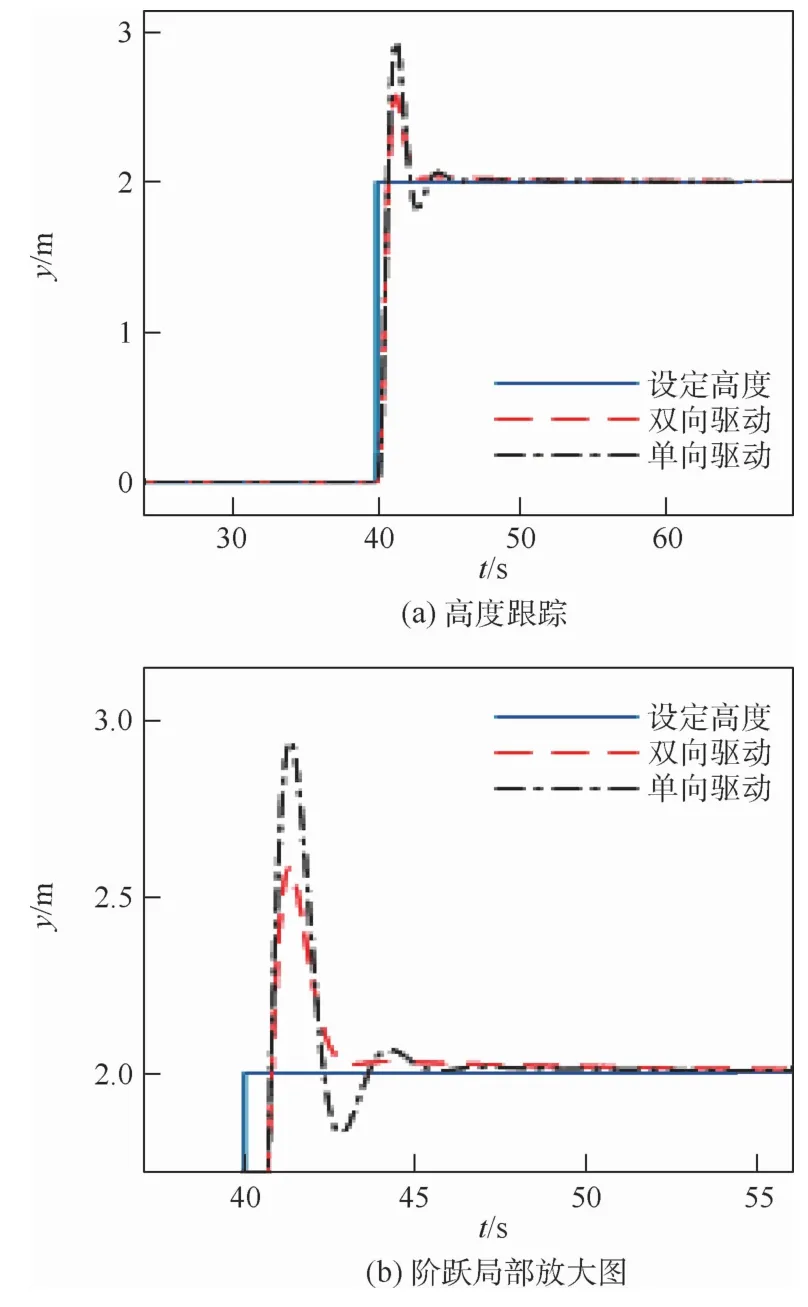
图10 高度跟踪结果Fig.10 Height tracking results
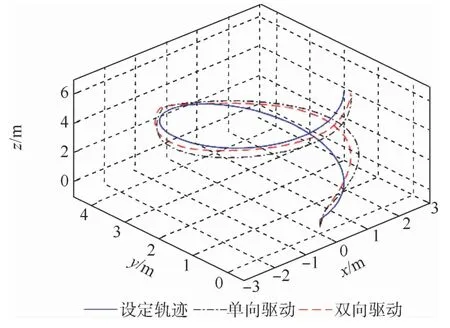
图11 螺旋曲线轨迹跟踪结果Fig.11 Tracking results of spiral curve
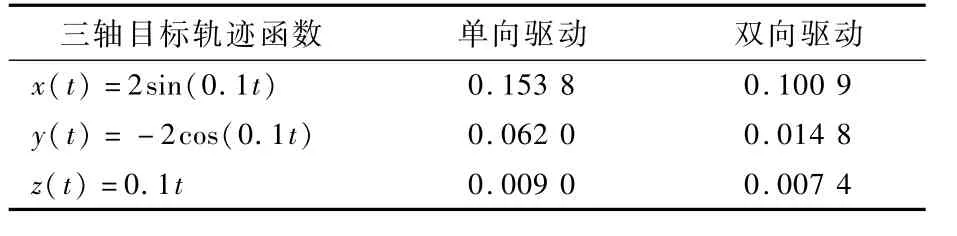
表3 两种模型与目标螺旋曲线轨迹之间误差的方差Table 3 Variance of errors between two models and target spiral trajectory
5 结 论
1)本文提出了一种具有固定桨距、双向电机驱动的新型四旋翼飞行器,基于四元数表达方法,对新型四旋翼进行动力学建模,设计了控制器和控制分配矩阵。
2)新型四旋翼通过双向电调输出双极性PWM波驱动电机,实现飞行中旋翼的快速减速或反转,从而提升旋翼转速变化的动态特性,并实现了旋翼的双向推力。
3)在仿真过程中,本文提出了一种轨迹生成方法,规划了实现翻转、点到点等机动飞行的轨迹,测试了新型四旋翼在姿态跟踪与轨迹跟踪方面的性能,结果显示该类飞行器与传统四旋翼相比,能有效提升机动性能。
后续将考虑翻转前后机体重心相对于机体几何中心偏移的影响,将在实物试验平台上进一步改进控制器及其控制分配方法,并进行充分的试验验证。
