舰载无人机滑行轨迹控制方法
2021-03-26梁天骄陈晓明杨朝旭王海峰梁庆
梁天骄,陈晓明,杨朝旭,王海峰,梁庆
(1.歼击机综合仿真航空科技重点实验室,成都610091; 2.北京航空航天大学 航空科学与工程学院,北京100083)
舰载无人机在现代海上战争中发挥着越来越重要的作用,由于其具有使用灵活和避免人员伤亡等优势,因此备受各国海军青睐[1-2]。舰载无人机滑行是航母甲板作业的重要组成部分,是指根据具体任务要求将舰载无人机从停放位置转移到指定位置[3-5]。滑行过程中,在考虑舰载无人机地面机动能力的前提下,如何控制其滑行轨迹对于安全高效完成滑行任务具有重要意义。
舰载无人机上由于没有驾驶员进行操纵,在滑行过程中,需要从外界获取控制指令信号,以保证滑行过程的顺利进行[6-7]。甲板上可供舰载无人机滑行的区域有限,且存在各种障碍物,这些都将对舰载无人机的滑行安全产生影响[8-10]。为实现舰载无人机在甲板上的自主滑行,研究滑行轨迹的控制方法,对于舰载无人机实时生成滑行轨迹和控制指令十分有必要。
根据不同的应用场景,舰载无人机有3种滑行模式,即自主滑行、无杆牵引滑行和有杆牵引滑行。其中,自主滑行与有杆牵引滑行主要用于舰载无人机在甲板上滑行的情形,而无杆牵引滑行主要用于机库中,以减少整个牵引系统占据的空间。针对以上不同的滑行模式,分别用不同的运动方程进行描述。自主滑行运动主要基于无人机的地面滑行进行描述[11]。与无人机相比,舰载无人机不能自主进行倒退,而且其运动速度也被限制在一个很小的范围内,保证紧急刹车时具有一定的安全距离。无杆牵引和有杆牵引滑行时的运动描述可见文献[12-13]。
关于舰载无人机甲板滑行轨迹规划与控制方法的研究,现有文献多集中在根据具体的调运任务设计路径规划算法,离线生成滑行轨迹对甲板障碍物进行规避[14-15]。目前的舰载无人机甲板滑行路径规划与跟踪控制方法可大致分为4类。第1类采用基于几何搜索方法生成滑行规划,如A*算法、Dijkstra算法等。这些路径规划算法能够规划出从滑行起点到终点所经过的路径点,再将相邻路径点顺次连接得到折线形式的滑行路径[16-18]。但折线形式的路径存在尖点,在实际滑行过程中舰载无人机不可能按照这样的路径运动。考虑舰载无人机滑行的机动能力,文献[19]通过计算舰载无人机转弯半径对折线形式路径的尖点进行修正。第2类是基于行为的方法,最初是被用于移动机器人的路径规划问题上,目前也被用于舰载无人机甲板滑行路径规划问题的研究。在此方法中,舰载无人机有奔向终点与规避障碍2种行为,舰载无人机滑行速度与航向角被当作是行为变量。这类方法在某种程度上与人工势场法相似,因为这2种方法都主要考虑势能场的设置问题[20]。第3类是基于智能优化算法的舰载无人机甲板滑行路径规划方法。文献[21]提出了一种聚类粒子群算法,可一次性为舰载无人机生成多条滑行路径。文献[22]基于鸡群算法提出了一种通用的路径规划算法,该算法能够使舰载无人机从甲板上不同位置滑行到目标点,并且能规避各类障碍物。第4类是动态优化方法,将所要解决的问题统一到最优控制问题模型的框架下。文献[23]提出用拉格朗日-高斯伪谱法求解舰载无人机甲板滑行轨迹优化问题,将滑行时间设为自由可变量,得到了满足所提出约束条件的滑行路径。
本文在以上研究的基础上,研究舰载无人机滑行轨迹控制方法,主要的创新点如下:
1)将轨迹规划与控制相结合,当规划出舰载无人机未来一段时间内的滑行路径后立即在线对此滑行路径进行跟踪,控制舰载无人机的运动。
2)在对生成的滑行路径进行跟踪时,以舰载无人机起落架前轮偏转角为控制变量,建立轨迹跟踪问题的数学模型。结合模型预测控制和滚动优化思想,提出了舰载无人机滑行轨迹控制方法。
3)所提出的方法能对已规划的路径进行在线跟踪控制,得到实际滑行轨迹,直接生成执行机构的控制指令信号,保证了舰载无人机能准确到达指定位置。
1 舰载无人机滑行问题
本节首先描述舰载无人机滑行轨迹控制问题的物理背景,在此基础上对此问题用规范的数学形式进行表示。
1.1 物理背景
航母甲板形状是不规则的多边形,甲板上舰载无人机会进行各种滑行任务,甲板环境及舰载无人机滑行任务描述如图1所示[24-25]。
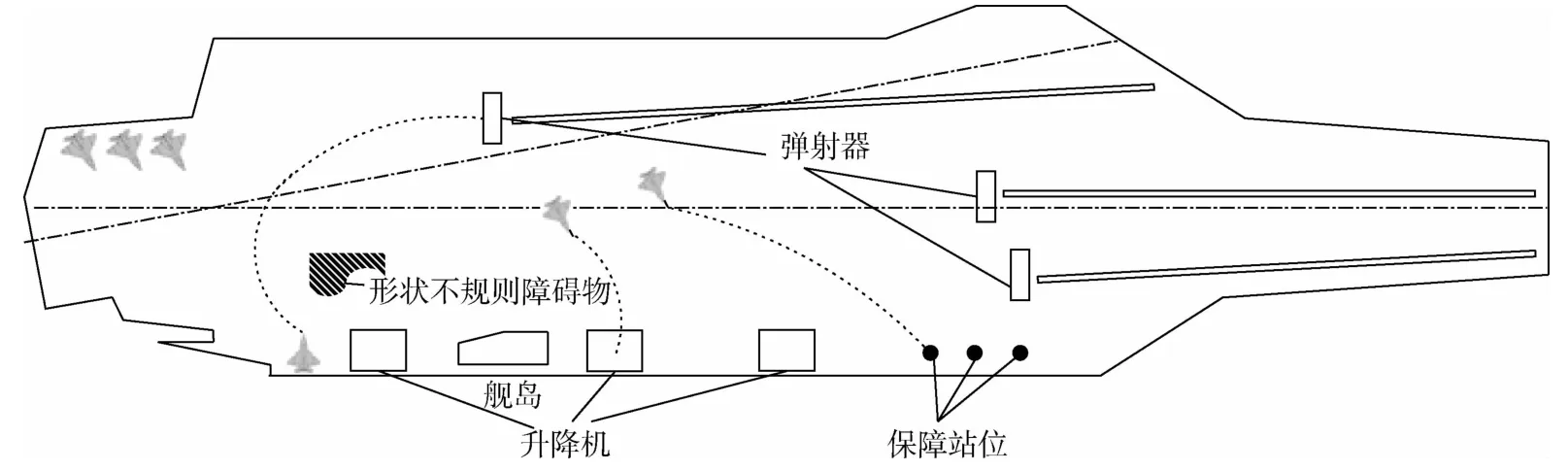
图1 甲板环境及舰载无人机滑行任务描述[24-25]Fig.1 Illustration of deck environment and taxiing task of unmanned carrier aircraft[24-25]
图1中,以“尼米兹”级航母为例,航母甲板上布置有弹射器,舰载无人机可滑行至弹射器位置进行起飞。升降机用于在机库与甲板之间调运舰载无人机,舰载无人机通过滑行至升降机调运回机库进行维修。另外,甲板上还设置了一定数量的保障站位,舰载无人机滑行到保障站位后可进行各项保障任务。在以上滑行过程中,舰载无人机可能会遇到障碍物,此时则需要绕过障碍物滑行。舰载无人机滑行轨迹控制的任务是寻找到一条满足其地面机动能力和任务要求的轨迹,并且使得实际滑行轨迹与已规划路径之间的误差尽可能得小。
1.2 数学表达形式
由以上对舰载无人机滑行问题的物理背景描述,定义离散时间点上的非线性映射f,则有以下状态方程:
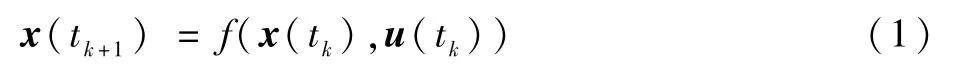
式中:x(tk)∈Rp为舰载无人机在采样时刻的状态,是一个p维列向量,代表p个状态变量;u(tk)∈Rq为舰载无人机在采样时刻的控制指令输入,是一个q维列向量,代表q个可操纵的执行机构;Rp和Rq分别为状态量和控制量所在的p维和q维空间。
可以看出,在任意采样时刻,当确定控制指令u(tk)后,x(tk)可通过映射f计算得到,f通常代表舰载无人机的地面运动方程。因此,舰载无人机滑行轨迹控制问题可描述为已知初始条件x(t0)=x0和舰载无人机在任意时刻t的理想状态xp(t)(由已规划路径获得),寻找控制指令序列u(t),满足滑行过程中某种性能指标J(t)最小。性能指标J(t)为
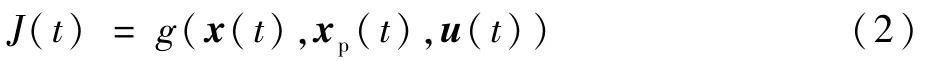
将状态变量xp(t)以离散时间序列的形式给出,采样时间间隔为Δt=tk+1-tk。设控制指令输入u(t)为分段常值函数,即将控制变量参数化,当tk≤t≤tk+1时,u(tk)=uk。通过解式(1),可得到x(tk+1)。因此,舰载无人机滑行轨迹控制问题转换为寻找控制指令序列uk,使性能指标J(tk+1)最小。要解决这一参数优化问题,需要建立舰载无人机地面运动模型,并建立起相应的状态空间。
2 轨迹控制问题数学模型的建立
舰载无人机在滑行过程中,必须时刻都在甲板的可行域内,以保证滑行过程的安全。本节首先建立舰载无人机地面运动模型,在此基础上设计轨迹控制任务的性能指标。
2.1 舰载无人机滑行运动模型
舰载无人机在甲板上滑行时,其动力来自于发动机,运动方向由前轮转角控制。所以上述模型可用三轮车的运动学模型来表示,运动模型如图2所示。
图2中:直角坐标系xdOdyd是以甲板中轴线末尾为原点建立的;(x,y)为舰载无人机质心的位置;v为舰载无人机在甲板上的滑行速度;φ为航向角;l为起落架前轮与后轮间的垂直距离;θ为起落架前轮的偏转角。舰载无人机滑行运动学模型可用以下非线性微分方程表示:

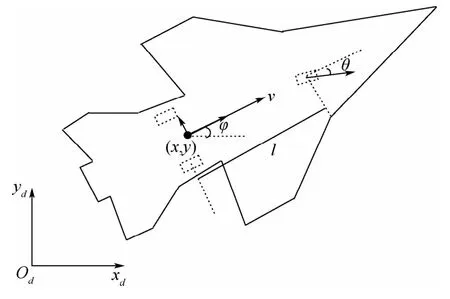
图2 舰载无人机地面运动模型示意图Fig.2 Schematic diagram of ground motion model of unmanned carrier aircraft
由于滑行是低速运动,且v=0.9~1.5m/s,变化范围不大,可将其处理为匀速运动。上述地面运动模型中,前轮偏角为控制量,且满足θmin≤θ≤θmax的约束,θmin和θmax根据舰载无人机前轮的机动能力来取值。
因此,在舰载无人机地面运动模型中,定义u(tk)=θk,x(tk)=[x(tk),y(tk),φ(tk)]T,(x(tk),y(tk))为舰载无人机质心的坐标,φ(tk)为舰载无人机滑行时的航向角。在采样时刻tk对式(3)~式(5)进行数值积分,可求解得到舰载无人机在下一时刻的状态信息x(tk+1)。
2.2 轨迹控制性能指标的建立
轨迹控制性能指标是针对下一时刻舰载无人机的状态与已规划轨迹间的差距进行评价。因此,应该以预测位置与已规划路径之间的偏差最小来构建轨迹控制性能指标。
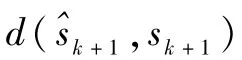

式中:dmax为允许的最大位置误差。

式中:γmax为允许的最大航向角误差。
最后,舰载无人机滑行轨迹控制问题的性能指标可以表示如下:
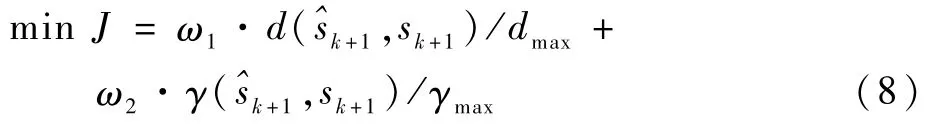
式中:ω1和ω2为反映不同性能指标项之间相对重要程度的权系数。
3 基于模型预测的轨迹控制方法
为实现对滑行轨迹的在线控制,本文将轨迹规划与控制相结合,在每一步轨迹规划结束后立即对获得的路径进行控制,直到完成对目标点的控制任务为止。每一步轨迹规划的方法可详见文献[19],此处不再赘述。跟踪轨迹时采用滚动时域控制方法[26],将固定时域内的参数优化问题转化为滚动优化问题,对轨迹控制性能指标进行优化,有效减少了轨迹控制误差。
3.1 轨迹控制方法的结构
基于模型预测[27]的轨迹控制方法结构包括预测模型和优化模型2部分,如图3所示。
图3中:预测模型根据k时刻舰载无人机的状态信息,选取不同的控制指令,计算得到k+1时刻舰载无人机可能的状态。而优化模型根据性能指标,在k+1时刻舰载无人机可能的状态中选择一个最优的,得到最优控制指令θk,并由舰载无人机地面运动模型计算得到k+1时刻的状态。

图3 轨迹控制方法结构示意图Fig.3 Structure of trajectory control method
3.2 加入模型预测控制的滚动优化方法
在规划一段直线路径后,需要采用轨迹控制算法生成控制指令序列来引导舰载无人机以最小偏差沿已规划路径运动。为保证滑行安全,本文基于模型预测的思想对控制指令进行滚动优化,在满足轨迹控制终止条件后完成滑行任务。
在图3基础上,预测模型不仅对k+1时刻舰载无人机可能的状态进行预测,而且还预测k+i(i=2,3,…,N)时刻的状态,再将这些预测的状态作为优化模型的输入。优化模型中存在预测域与执行域的概念,如图4所示。
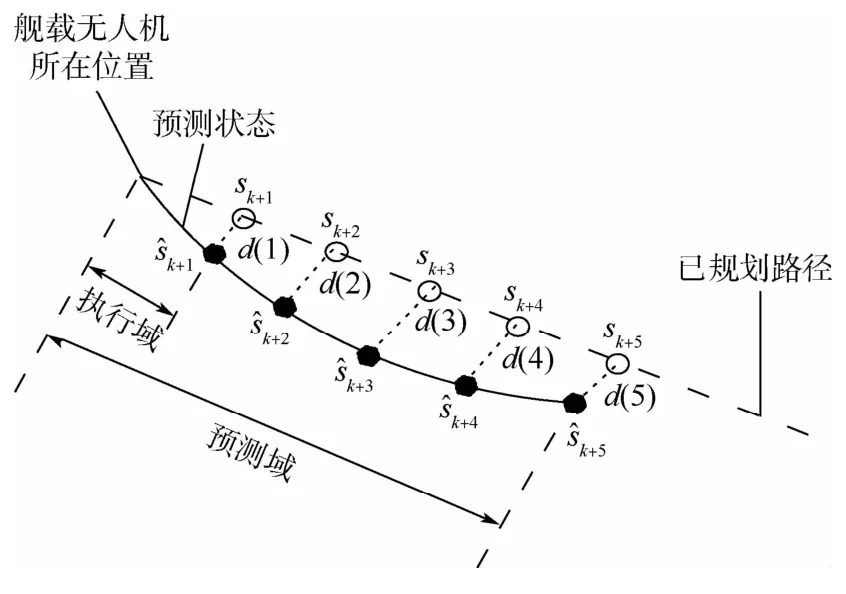
图4 轨迹控制过程描述Fig.4 Description of trajectory control process
以N=5为例,图4中,空心圆点sk+1为k+i时刻已规划路径中舰载无人机的位置,实心圆点为时刻舰载无人机的预测位置;k+i时刻的位置误差d(i)在图4中用细虚线表示。实际运行时,为保证舰载无人机滑行安全,需要严格地按照时间顺序对已规划的路径进行在线控制。预测域(设预测时间为Tp)给出了tk后5个采样时刻的状态信息,而优化模型对这些信息进行综合处理,通过性能指标计算出此时最优的控制指令序列。执行域(设执行时间为Te)只在tk≤t≤tk+1时执行以上控制指令,作用于舰载无人机前轮。当t=tk+1时重新进行上述滚动优化过程,直到完成对已规划路径的控制。随后继续规划下一段直线路径,再重复以上轨迹控制过程,如此循环,直到完成对整个规划路径的控制任务。
上述滚动优化过程中,轨迹控制性能指标是针对未来一段时间内舰载无人机的状态进行评价的,因此可将式(8)的性能指标修改为
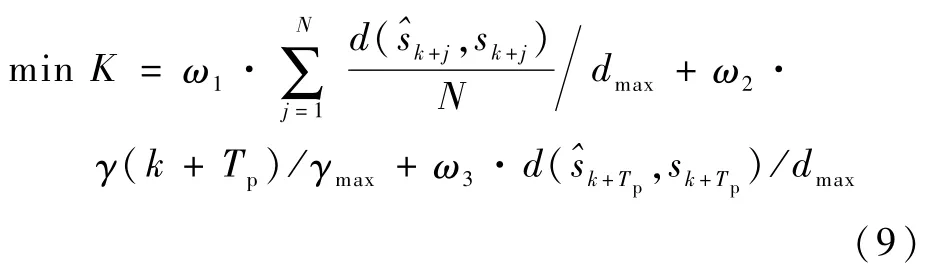
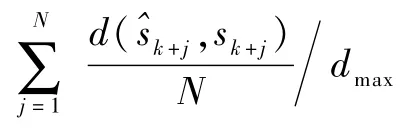
由于本问题中控制量为舰载无人机前轮偏角,在对式(9)的指标进行优化时,需要确定规划域内每个采样时刻的前轮偏角值,即θk,θk+1,…,θk+N-1。由于舰载无人机的前轮偏角范围通常较小,为减少计算量,将θ在其允许范围内(θmin≤θ≤θmax)等距地离散为M个值,即

m为θ离散为M个值后每个离散值θm的编号。对于每组可能的[θk,θk+1,…,θk+N-1]序列,分别代入式(3)~(5)计算出舰载无人机的状态值,再将以上结果代入式(9)计算出滚动优化每个规划域中的性能指标,将最小指标值所对应的[θk,θk+1,…,θk+N-1]序列作为当前规划域的最终优化结果。
3.3 轨迹控制方法流程
3.2节详细介绍了舰载无人机滑行轨迹控制方法,为避免轨迹控制过程陷入循环,设置轨迹控制结束条件如下:
1)已完成对所有已规划路径的控制,无论舰载无人机是否已到达指定位置,轨迹控制过程结束。
2)舰载无人机若进入指定位置周围一定范围内,无论是否完成对已规划路径的控制,轨迹控制过程结束。
以上2个条件只要至少满足1个,则轨迹控制过程结束。舰载无人机轨迹控制的流程如图5所示。
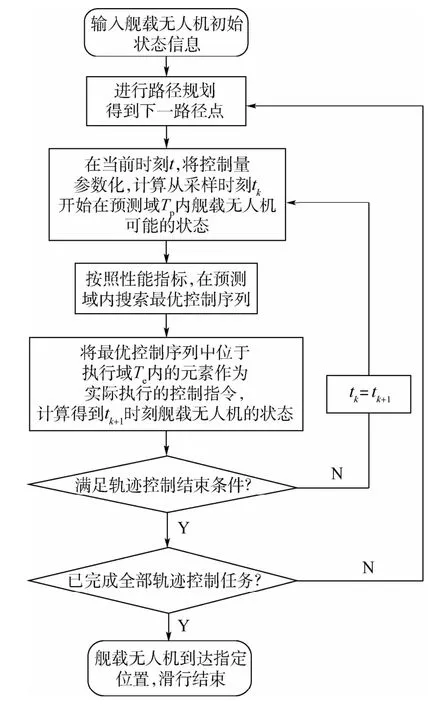
图5 舰载无人机轨迹控制方法流程Fig.5 Flowchart of trajectory control method for unmanned carrier aircraft
图5中:有2处判断是否完成轨迹控制的语句。第1处是判断是否完成对一段直线路径的控制,而第2处是判断是否完成对已规划的最后一段直线路径的控制。2处均以前面描述的2条轨迹控制结束条件进行判断。
4 算例仿真
本节以起飞任务为例,在MATLAB R2009a编程环境下采用提出的轨迹控制方法对在不同停放位置的舰载无人机滑行至弹射器的过程进行仿真,得到舰载无人机实际滑行路径,并对结果进行了统计与分析。
4.1 算例模型及参数设置
以美国“尼米兹”级航母为例,用提出的轨迹控制方法得到在不同停机位停靠的14架舰载无人机各自的实际滑行路径。算例模型示意图和各舰载机起飞位置的设定分别如图6和表1所示。
表1中:14架舰载无人机分别在3台弹射器上完成起飞。需要注意的是,本文不考虑各架舰载无人机在滑行过程中的相互干扰,因为这属于多机协同问题,已超出了本文的研究范围。轨迹控制的目标是使得各架舰载无人机能滑行到指定位置,且尽量减少跟踪误差。
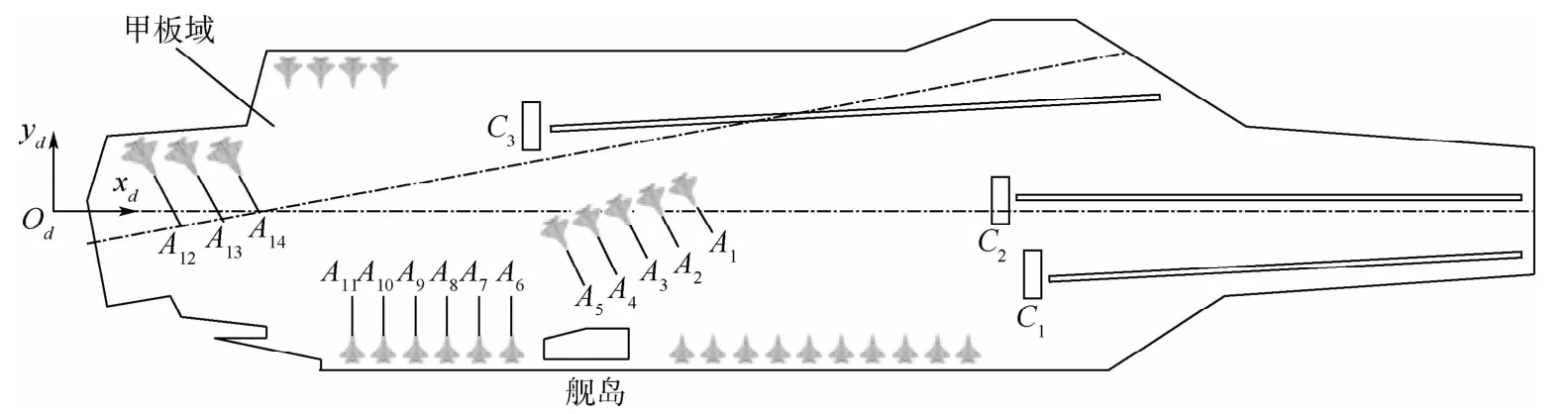
图6 算例模型示意图Fig.6 Schematic diagram of simulation model of an example
4.2 算例仿真结果
根据各舰载无人机的起飞位置信息,将控制变量(起落架前轮偏转角)在其取值范围内离散为θ=[0°,±5°,±10°,±15°,±20°,±25°,±30°],设置θ初值θ(0)=0°,舰载无人机滑行速度为5 ft/s(1 ft/s=0.3048m/s),允许的最大跟踪误差dmax=2 ft,允许的最大航向角跟踪误差γmax=π/4,按照基于模型预测的滚动优化轨迹控制算法流程,得到每架舰载无人机的规划路径与实际滑行路径,均绘制在图7中。
从图7可以看出,各架舰载无人机机均能够跟踪所规划的轨迹滑行到指定位置。图8以A1为例给出了滑行过程中舰载无人机前轮偏转角随时间的变化曲线。

表1 舰载无人机起飞位置Table 1 Launching position of unmanned carrier aircraft
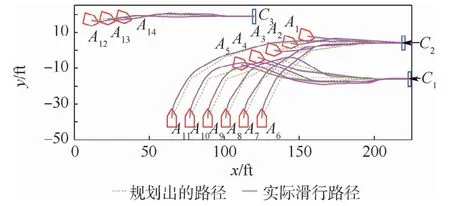
图7 舰载无人机实际滑行路径Fig.7 Actual taxiing path of unmanned carrier aircraft
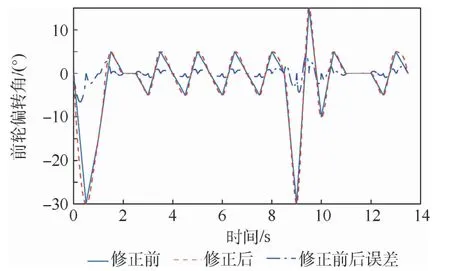
图8 滑行过程中A1 前轮偏转角变化曲线Fig.8 Curves of nosewheel deflection angle of A1 during taxiing
可以看出,在滑行过程中,A1的前轮偏转角始终在允许的偏转范围内,满足地面机动能力要求,前轮偏转角经3次样条曲线拟合后成为平滑曲线,在实际过程中能够为自动器提供可靠的指令信号控制滑行过程,且修正前后前轮偏转角误差在很小的范围内变化。
仿真算例中,各舰载无人机滑行时间、滑行轨迹终点与期望终点位置的误差如表2所示。
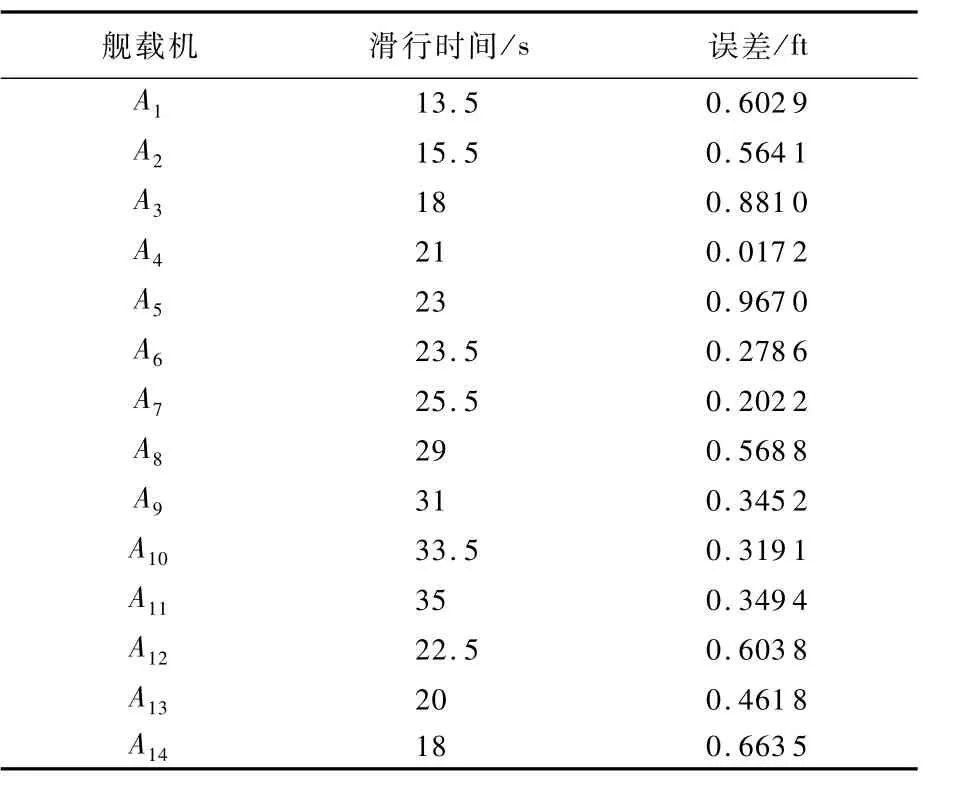
表2 滑行时间与轨迹控制误差Table 2 Taxiing time and trajectory control error
由表2可计算出平均轨迹控制误差为0.487 5 ft≈0.148 6m,满足滑行任务的要求。以上仿真结果表明,本文提出的方法能对规划的直线路径进行在线轨迹控制,生成舰载无人机滑行的实际路径与控制指令信号,且路径控制误差较小。
5 结 论
1)以优化舰载无人机实际滑行轨迹为目标,对舰载无人机滑行轨迹控制问题进行描述。在此基础上建立了滑行轨迹控制问题的数学模型,包括舰载无人机地面运动模型和轨迹控制任务的性能指标。
2)提出了基于模型预测的轨迹控制方法,采用滚动时域控制方法对轨迹控制性能指标进行优化。将路径规划与轨迹控制相结合,对已规划路径进行在线控制。
3)算例以起飞任务为例,对舰载无人机滑行过程进行了仿真,仿真结果给出了舰载无人机的规划路径与实际滑行轨迹、控制指令信号、滑行时间和轨迹控制误差。
结果表明,本文建立的数学模型和提出的轨迹控制方法能完成在线轨迹控制任务,生成舰载无人机实际滑行路径和控制指令信号,且控制效果较好。本文的研究成果能为自动器提供可靠的控制指令信号,保证舰载无人机滑行任务安全高效完成。
