欠驱动变质心飞行器的滚偏耦合自抗扰控制

刘智陶，李涧青，高长生

（1.中国工程物理研究院 总体工程研究所，绵阳621999； 2.浙江大学 电气工程学院，杭州310000；3.哈尔滨工业大学 航天学院，哈尔滨150001）

变质心控制（Moving Mass Control，MMC）技术利用内部可移动质量块使系统质心产生偏移，通过调整气动力臂的方式获得控制力矩改变运动姿态［1-5］。该控制技术相较传统气动舵面控制和喷气控制能够良好解决舵面烧蚀、气动外形保持、侧喷扰流和燃料限制等工程应用难点［6-10］，充分利用气动力的作用并具有小滑块位移产生大幅控制力矩的效果［11］，故在大气层内再入机动飞行器领域持续受到国内外学者的广泛关注［12-16］。

单滑块滚控式（Moving Mass Roll Control，MMRC）方案依靠不对称升力体气动外形产生固定配平攻角，由横向配置单滑块控制滚转调整升力面方向实现倾斜转弯（Bank-To-Turn，BTT）机动。Petsopoulos等［17］基于二次型调节器设计了滚转自动驾驶仪，并通过数值仿真进行了可行性验证，提出该构型方案因布局简单、易于工程实现和具有高控制效率而值得深入探讨；王林林等［18］利用标准系数法设计了滚转控制器，仿真结果表明，该控制器能够在一定程度上解决跨空域飞行的系统参数时变问题；Su等［19］应用轨迹线性化方法设计了滚转控制器，气动参数摄动下仿真验证了控制器的鲁棒性；李自行和李高风［20］基于拉格朗日法建立了系统姿态运动模型，并针对滚转单通道设计了标准二阶自抗扰控制器，仿真结果相比传统PD控制更能适应参数扰动；范一迪等［21］采用频域法分析了滑块偏移对姿态运动的耦合影响，并设计了滚转单通道PD控制器，分析结果表明，滚控式变质心飞行器能够通过小质量比滑块实现有效滚转控制，但控制过程将耦合影响偏航通道。

高速快时变运动下的通道交叉耦合、滑块偏移造成的运动耦合、气动不对称外形产生的动力学非线性和飞行环境的不确定性均导致整个变质心飞行器系统在再入过程中处于强耦合、强非线性和强扰动状态。以往针对单滑块构型的研究通常考虑单个滑块主动控制单个通道，而另外两通道则由气动静稳定性或结合其他控制机构维持稳定。然而，增加额外控制机构势必加重系统复杂程度且会带来其他未知问题，仅依靠气动静稳定性又难以适应强扰动飞行环境，故如何充分挖掘单滑块的耦合欠驱动控制能力，实现通过单滑块偏移在稳定跟踪制导指令的同时对其他通道实施镇定控制并进一步增强姿态控制系统的抗干扰能力，是值得研究的问题之一。解决欠驱动控制问题的常用方法包括级联分析法［22］、最优控制［23］和能量控制法［24］等，由韩京清［25］提出的自抗扰控制（Active Disturbance Rejection Control，ADRC）以及扩张状态观测器（Extended State Observer，ESO）和总和扰动动态补偿为核心，具有不依赖具体数学模型和能够抵抗系统内外扰动的强鲁棒性能，特别适用于处理存在强不确定性的复杂系统控制问题，且结构简单易于实现，该技术在电机控制［26］、卫星姿态控制［27］和机器人运 动控制［28］等工业领域已得到成功应用。

本文首先建立了单滑块滚控式变质心飞行器的系统姿态动力学模型；其次，考虑整个非线性系统的滚偏强耦合特性，提出了耦合欠驱动自抗扰控制器；最后，通过数值仿真对控制器的有效性、动静态品质和鲁棒性进行了验证分析。

1 系统姿态动力学模型

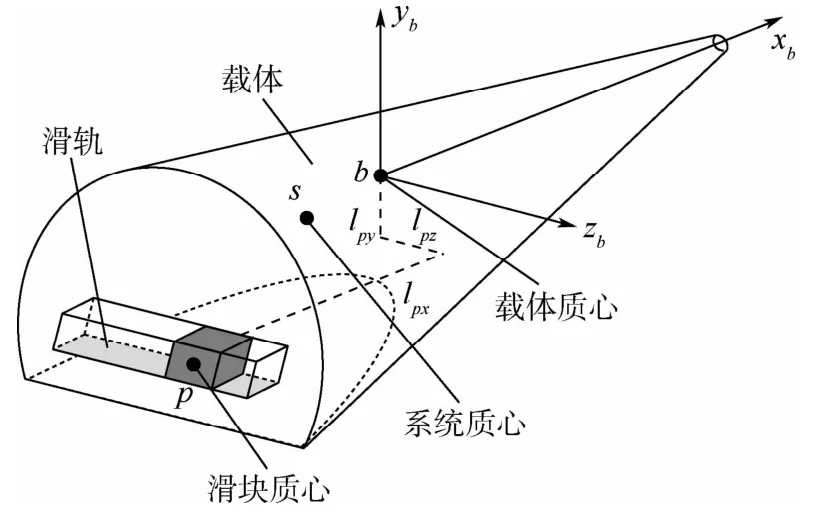
图1 单滑块滚控式变质心飞行器示意图Fig.1 Sketch map of flight vehicle with single moving mass roll control

本文考察对象如图1所示，整个飞行器系统S主要由载体B和内部单滑块P构成，3者质心分别用s、b和p表示。飞行器为采用切削圆锥体的面对称构型，内部单滑块可在伺服机构驱动下沿滑轨垂直于载体纵对称面移动，经气动力作用产生滚转控制力矩调节升力面方向，进而达到姿态控制和弹道机动目的，俯仰通道则依靠气动纵向静稳定性维持稳定。

定义载体系obxbybzb的原点为b，obxb轴沿载体轴线指向头部，obyb轴在载体纵对称面内垂直于obxb轴指向上方，obzb轴构成右手直角坐标系；lpx、lpy和lpz为滑块质心在载体系下位置坐标；mS、mB和mP分别为系统质量、载体质量和滑块质量，有mS=mB+mP；μP为滑块质量比，有μP=mP/mS；rbp为从载体质心b指向滑块质心p的位置矢量。根据质点系动量矩定理可建立载体系下系统姿态动力学方程矢量式为［17］

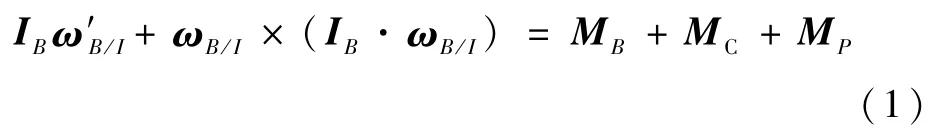
式中：（·）′为矢量在载体系下一阶导数；IB为载体对其质心的转动惯量矩阵；ωB/I为载体系相对于惯性系的旋转角速度；MB=rbQ×R为作用于载体质心上的气动力矩，Q为飞行器气动压心，rbQ为从载体质心b指向气动压心Q的位置矢量，R为总气动力；MC=-rbs×R为滑块偏移产生的附加气动力矩，是变质心控制力矩，rbs为从载体质心b指向系统质心s的位置矢量；MP为滑块运动产生的惯性力矩，其表达式为

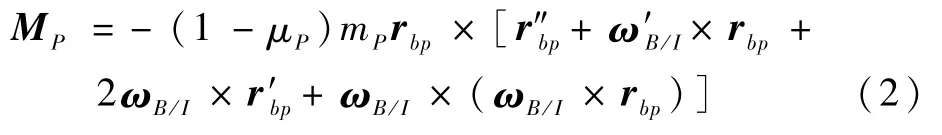
式中：（·）″为矢量在载体系下的二阶导数。

总气动力和气动力矩分别在速度系和载体系下表示为

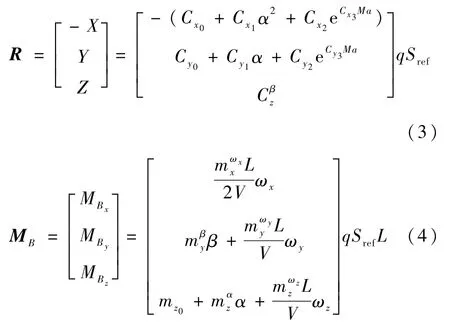
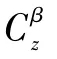
考虑滑块初始位置与载体质心重合，在载体系下展开式（1）可得系统三通道完整耦合姿态动力学方程为

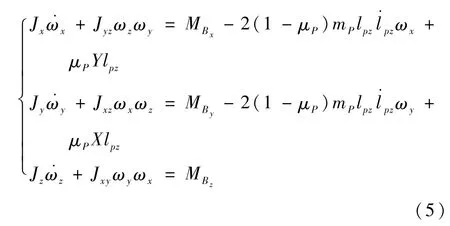
式中：

其中：lpz和分别为滑块横向偏移量和偏移速率；Ixx、Iyy和Izz分别为载体主转动惯量在载体系的三轴分量。

观察式（5）可知，俯仰通道无控制输入lpz且主要为运动学耦合，其通道稳定由气动纵向静稳定性保证。而滚转和偏航通道同时存在通道交叉耦合项和滑块惯性耦合项，且μPYlpz和μPXlpz项分别为滚转和偏航通道所受滑块控制力矩，两通道拥有同一个控制输入lpz，说明滑块跟踪滚转角指令发生频繁偏移过程中会对偏航通道产生耦合影响，因此滚偏耦合严重，加之实际飞行环境中气动参数的不确定性和未建模扰动的存在均可能导致侧滑扰动产生，对姿控系统带来不利干扰。

滑块伺服运动近似为二阶振荡模型：

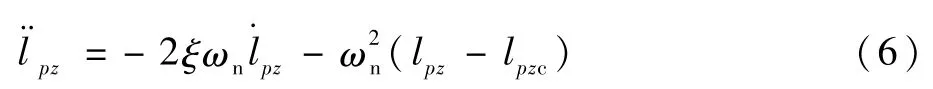
式中：ξ、ωn和lpzc分别为阻尼比、无阻尼自振角频率和滑块指令偏移。

2 耦合欠驱动自抗扰控制器

为解决指令滚转角跟踪过程中的侧滑角镇定问题，本节设计滚偏耦合欠驱动自抗扰控制器。假设攻角为小量且滚转角一阶导数近似滚转角速度，经化简可得［29］

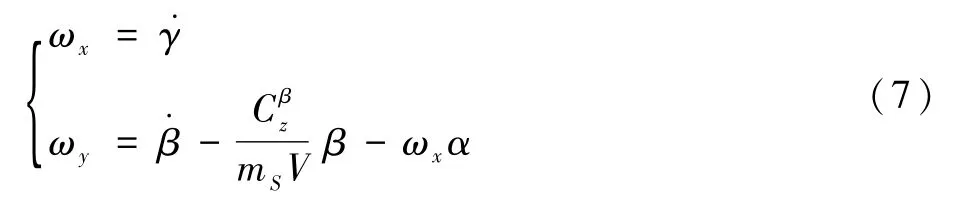
式中：f为已建模扰动矩阵；b为控制量输入矩阵。

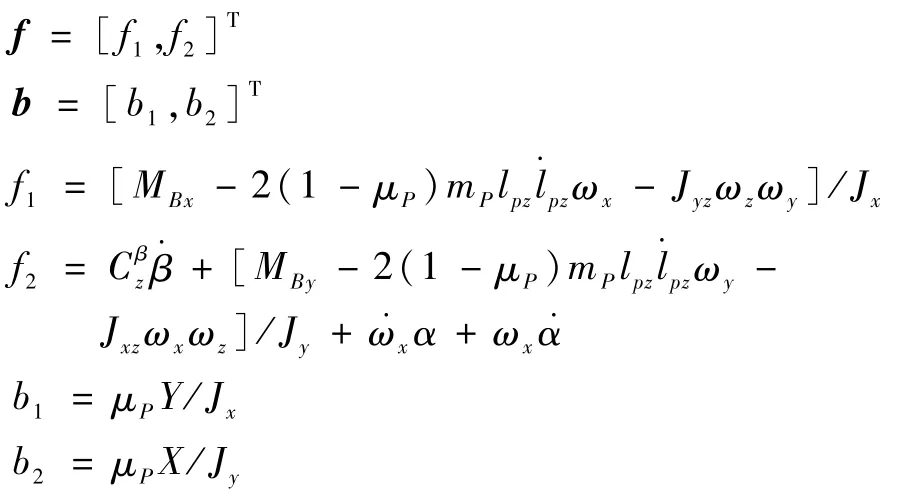
由于实际飞行过程中存在气动参数摄动导致控制量输入矩阵b并非精确值，故用包含参数摄动项的bd代替b，并令b0为bd在气动参数取参考值时的标称值；同理，用包含参数摄动项和未建模扰动项的fd代替f，则整个耦合系统的总和扰动项可定义为

式中：u表示实际控制输入lpz。

因此，式（8）可改写为

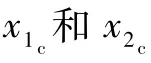
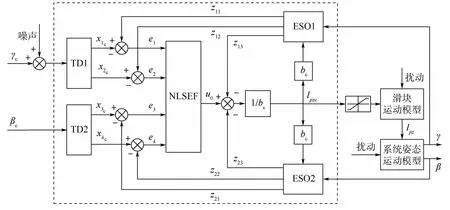
图2 变质心耦合欠驱动自抗扰控制框图Fig.2 Block diagram of ADRC-based moving mass coupling underactuated control

跟踪微分器的离散公式为［30］

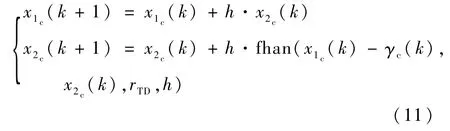
式中：h和rTD分别为采样周期和速度因子。TD1和TD2为2个相同的跟踪微分器，离散公式均采用相同形式与参数值。

扩张状态观测器的离散公式为［30］

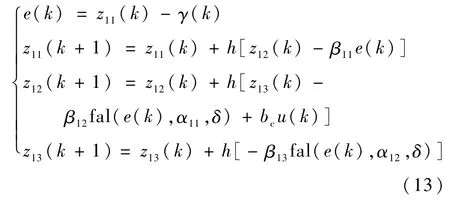
式中：β11、β12和β13为观测器增益；γ（k）为第k次采样周期的实际滚转角值；bc为动态补偿因子；z11（k）、z12（k）和z13（k）为第k次采样周期ESO1估计的滚转角、滚转角一阶导数和滚转角跟踪子系统总和扰动；α11和α12为可调参数。

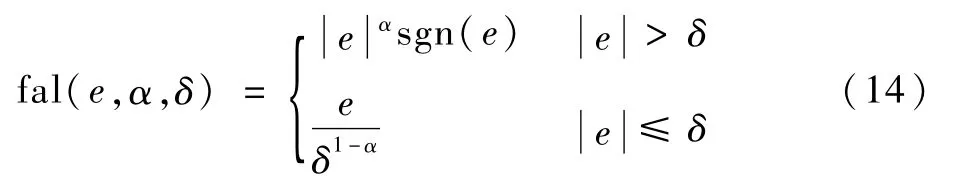
式中：e、δ和α均表示函数fal（·）的输入参数。ESO1和ESO2为2个相同的扩张状态观测器，离散公式均采用相同形式，并且由于滚转角跟踪子系统和侧滑角镇定子系统处于同一时间尺度，2个观测器使用相同参数。

改进的非线性状态误差反馈的离散公式为

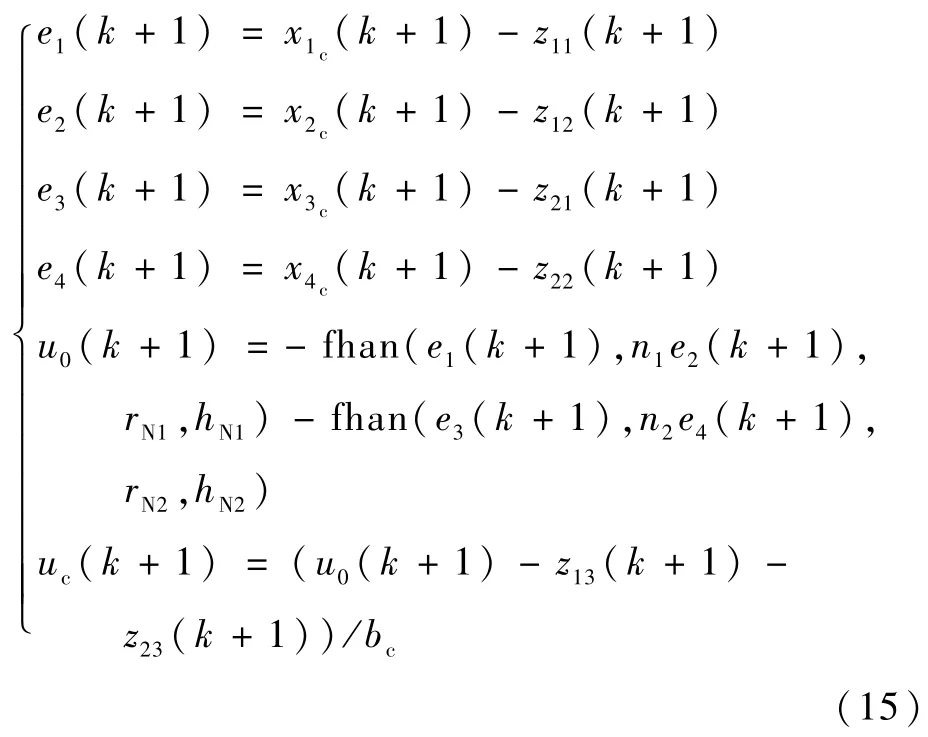
式中：n1、rN1、hN1、n2、rN2和hN2为非线性控制器参数；x3c（k+1）和x4c（k+1）分别为第k+1次采样周期TD2跟踪的指令侧滑角信号和及其微分信号；z21（k+1）、z22（k+1）和z23（k+1）分别为第k+1次采样周期ESO2估计的侧滑角、侧滑角一阶导数和侧滑角镇定子系统总和扰动。该控制器使用2个非线性函数fhan（·）对2个子系统的状态误差进行综合反馈控制，并对其总和扰动进行同时动态补偿，最终输出一个控制指令uc。

考虑本文所提出的耦合欠驱动自抗扰控制器具有多个待设计参数，给人工调节过程带来较大困难，采用粒子群优化（Particle Swarm Optimization，PSO）［31］方法进行参数设计。由于TD参数可独立整定，其采样周期h通常为积分步长的1～3倍，速度因子rTD影响过渡过程，过大rTD将加剧噪声，ESO的参数α11、α12和δ通常取固定值，故最终需要优化的参数为β11、β12、β13、n1、rN1、hN1、n2、rN2、hN2和bc。为兼顾滚转和偏航通道的动静态品质，设计如下适应度函数：

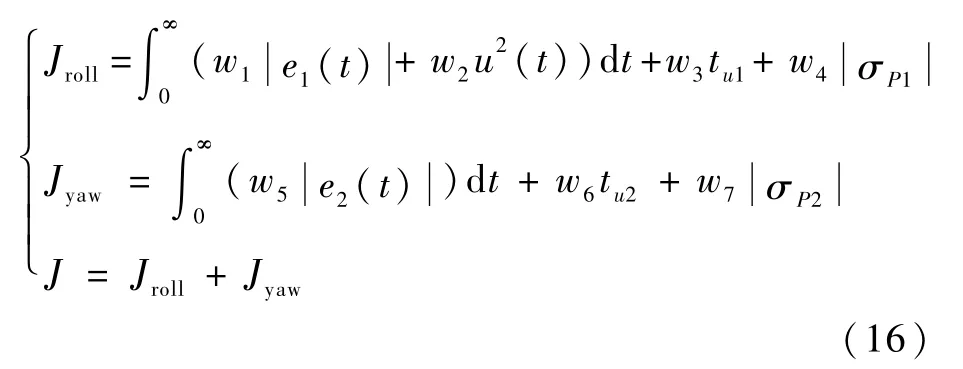
式中：Jroll、Jyaw和J分别为滚转通道、偏航通道和综合适应度函数；e1（t）和e2（t）分别为滚转角和侧滑角实时跟踪误差；u（t）为控制能量；tu1和tu2为上升时间；σP1和σP2为超调量；w1、w2、w3、w4、w5、w6和w7为各指标的权重系数。优化问题则转化为在可行域内寻找一套控制器参数使得适应度函数J达极小值。

3 仿真分析

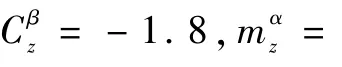
图3 滚转角跟踪结果Fig.3 Tracking results of roll angle

图4 侧滑角镇定结果Fig.4 Stabilization results of sideslip angle

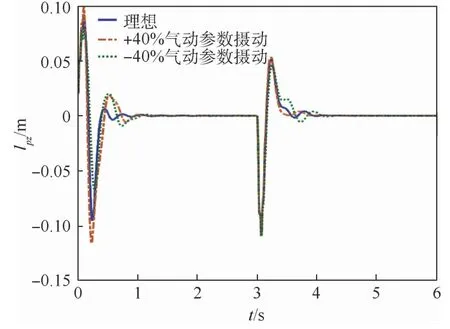
图5 滑块横向偏移曲线Fig.5 Lateral offset of moving mass

由图3滚转角跟踪结果和图4侧滑角镇定结果可知，两者均可在单滑块控制下有效跟踪指令信号，且具有期望的动态性能和稳态精度，即使在大幅参数扰动下仍可快速收敛，解决了在跟踪指令滚转角同时的侧滑角镇定控制问题；由图5可知，滑块在初始阶段表现出快速响应，随后逐渐稳定；图6和图7分别为ESO1和ESO2的状态观测误差曲线，观测误差在经过短暂振荡后迅速收敛至零，收敛时间短于姿态角收敛时间，表明状态观测值快速收敛至其真实值，确保了整个耦合欠驱动自抗扰控制器的稳定运行。

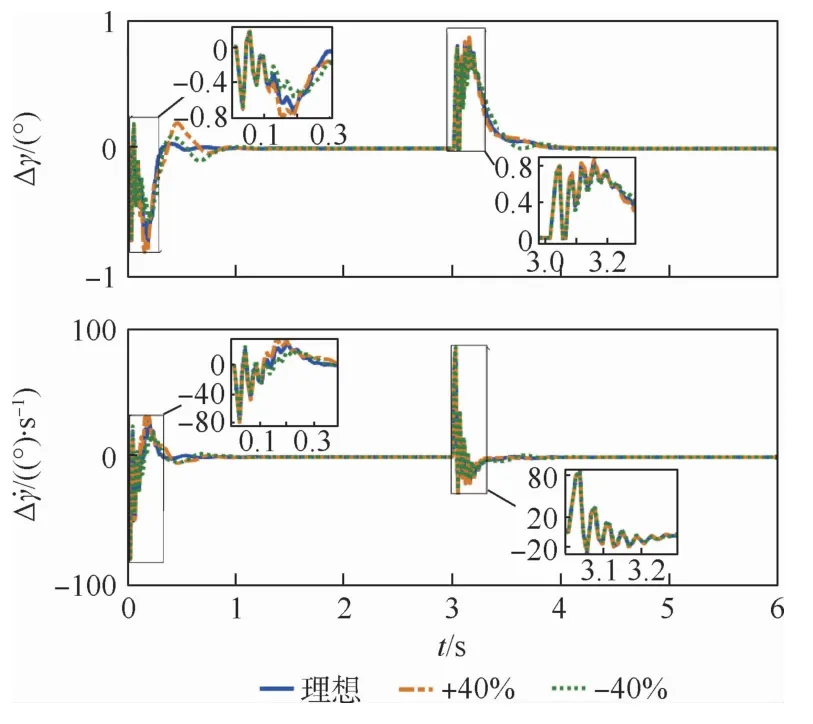
图6 ESO1状态观测误差曲线Fig.6 State estimation errors of ESO1

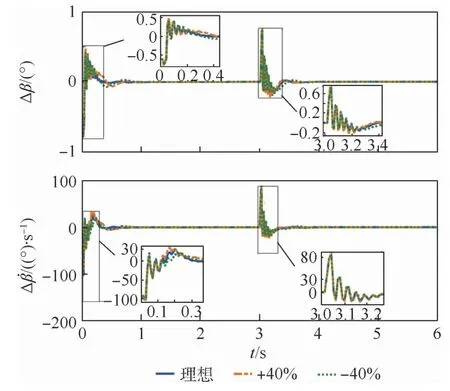
图7 ESO2状态观测误差曲线Fig.7 State estimation errors of ESO2

4 结 论

1）耦合姿态动力学方程表明，滚转和偏航通道同时存在通道交叉耦合项和滑块惯性耦合项，且两通道拥有同一个控制输入，滑块横向偏移会对偏航通道产生影响，因此滚偏耦合严重。

2）由于增加了侧滑角镇定子系统的扩张状态观测和总和扰动动态补偿，提出的欠驱动自抗扰控制器能够达到跟踪指令滚转角的同时实施侧滑角镇定控制的目的。

3）摄动对比仿真结果验证了横向配置单滑块的耦合欠驱动控制能力，所设计的控制器能够适应较大幅度的气动参数扰动，且具有较好动态品质和稳态精度，进一步增强了姿控系统的抗干扰能力。