风力发电机组优化控制策略研究

胡博，李麟

（中国电建集团河北工程有限公司，河北 石家庄 050000）

0 引言

近年来，随着我国能源机构改革的不断深化，新能源在电力系统中的占比正在不断提升，其中较为重要的部分则是风力发电机组。为实现并网发电，风力发电机组通常以电力电子装置并入电网当中，但由于风力发电机组受环境影响较大，出力不稳定，且很难进行有效预测，其发展受到了一定程度的限制，如何通过优化控制策略解决上述问题，仍需要进一步分析研究。

1 风电机组模型概述

为确保风力发电机组有着更高的发电效率，当前在电力系统中主要采用变速风力发电机，其又可分为双馈感应风力发电机组（DFIG）和永磁直驱同步风力发电机组（PMSG），其中以后者相对较为常见[1-2]。PMSG的主要结构分为风力机、传动链、永磁发电机、机侧变换器和网侧变换器五部分[3-4]。

在风力发电机组中，风力机是首要的工作模块，其在风力的推动下，桨叶开始旋转，完成空气动能到机械能之间的转换。对于给定的一个风力发电机组，其具有固定的风能利用系数 ，据此可进一步推导出发电机组的机械功率 ，计算公式如下：

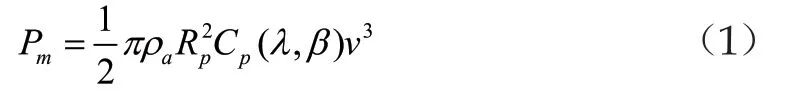
风电机组的传动链用于连接PMSG的转子和风力发电机的转轴，在实际研究中，传动链模型可抽象为单质块模型，计算公式如下：

为确保风力发电机组与电网实现有效对接，实现风力发电机电能的平稳输送，在实际工作中通常采用变换器。变换器可分为电网侧变换器和机侧变换器，其中又以机侧变换器较为重要，在优化控制工作中，主要针对机侧变换器进行频率控制，控制方法则为矢量控制。具体来看，首先需要建立dq坐标系，对发电机定子侧的输出有功功率进行计算，计算公式如下：

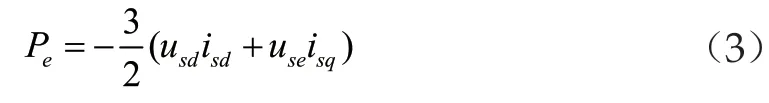
在式（3）中，括号中的前项和后项分别表示定子在d轴和q轴上的电压和电流之乘积，即为定子在d轴和q轴上的功率，其中也包含一定比例的无功功率，需要对其进行解耦。为此，考虑到d轴和q轴上的电流存在差异，因此分别对其依次进行闭环控制和逆变换等环节，再使之经过PWM发生器进行处理，即可输出相应的控制信号，以实现对发电机输出有功功率的有效调节。一般来说，当风力发电机组处于最大功率跟踪模式（即MPPT模式）下，有着最高的发电效率。根据这一理论，则需要通过调频，确保风力发电机组始终处于MPPT模式，其主要通过附加频率控制器实现。

2 风力发电机组的频率控制方法

2.1 有功增发阶段

风力发电机组在实际运行时，受到外界环境的影响后容易出现系统功率不平衡的问题，进而引发电网频率出现变化，其需要通过机组自身的惯性响应以及一次调频参与系统的频率调节，但机组自身的惯性响应能力相对有限，通常依靠机组的一次调频加以进行。该环节主要调整的内容是频率的变化率和差值，通过减小频率变化率和差值，来避免因频率变化过大而引发的电网不稳定等问题。在实际应用时，风力发电机组的大规模并网会导致在相同负荷扰动情况下产生更大的频率偏差和频率变化率，为控制上述问题，风力发电机组必须通过快速的功率调节来替代同步机组的惯性响应，才能实现预期目标，该环节主要在有功增发阶段进行，此阶段的输出功率可用公式表示：

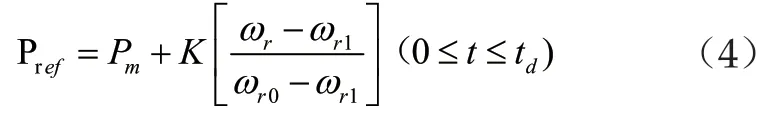
在式（4）中，K为比例系数， 为风电机组频率控制介入前的转速， 为频率控制解除后风电机组的转速，则为风电机组释放旋转动能的时间。当风电机组调频模块介入时， 达到峰值，随着时间的推移逐步递减，当时间为 时，转速变为恒定值，此时机械功率全部用于输出。

2.2 无备用风电机组转速的恢复

无备用发电机组与上述发电机组不同，在有功增发阶段完成后，其转速和机械功率均已显著降低，且同步机组的备用功率通常不足以再进行一次调频，此时如再出现频率降落则容易影响到系统的稳定性。为规避上述问题，在相关的研究工作中，工作重点在于如何确保无备用发电机组功率尽快恢复正常值，在这一阶段中，优化控制的主要目的是，将转速恢复阶段的时间尽可能降低，并避免频率再次降低。在这一阶段中，风力发电机组输出功率可用公式表示：

在式（5）中，为大于0的参数，为转速恢复的持续时间。为实现上述优化机制的目标，需要采用频率支撑方法加以实现。在这一方法控制下，可利用输出功率快速增大来降低系统频率的变化率和最大频率偏差。

2.3 减载控制

为确保风力发电机组实现一次调频，在风力发电机组稳定运行时，需要采用减载控制方法。为尽量降低机械磨损，超速法是减载控制方法中的首选，该方法也通常使用桨叶距角控制法加以辅助，以避免转速达到最大值时无法实现减载控制的问题。减载控制策略取决于以下两个要素：风速和减载率。在实际运行时，有功功率和最大功率的百分比，其与减载率的总和始终为100%，对于实际与理论情况而言，减载率通常在0~30%区间内。

对于风速这一要素而言，其通常将风速按照大小分为三个区间，在风速较小时，仅采用超速法即可实现减载控制，此时桨叶距角保持在0°不变；当风速适中时，减载控制方法以超速法为主，同时以桨叶距角的调整作为辅助；当风速过大时，仅应用调整桨叶距角的方法进行减载控制。具体的风速区间临界值则通常由样条插值法求出，减载率越大，临界值也越小。

2.4 调频系统概述

调频系统由参数优化模块、频率控制器、桨叶距角控制单元、风电场控制系统和减载控制等多个部分所组成，以实现变频控制作用。具体来看，如发电机组工作频率变化值较大，则调频功能自动开启，并接收来自风电场控制系统的增发功率指令，获取实际的增发功率。同时，为确保在一次调频后即能实现风力发电机组的优化控制，参数优化模块内置了智能算法，其会以机械功率为变量，实时计算桨叶距角和转速的最优值，并将这两个结果输入到桨叶距角控制单元当中。风电机组的转速也会同时输入到频率控制模块中，其目的是调节输出功率的增发值。

当风速已经超出区间III的临界值时，无备用的风力发电机组转速已经达到上限，此时必须通过控制桨叶距角来实现优化控制，以降低风能的输送量。在调频功能介入的初始阶段，风电机组的输出功率相对较高，其目的是降低频率的变化率，以及避免频率的偏差值过大。同时，通过控制单元对桨距角和转速的控制，发电机的机械功率也逐渐增大，实现最大风能跟踪控制，进而确保风力发电机组在新的工况下保持稳定。在这一过程中，除了发电机组输出功率外，其他参数并无明显变化。

2.5 频率控制器参数的优化

遗传算法属于并行搜索算法的一种，其算法流程与自然界的种群遗传规律较为相似。在遗传算法中，个体被称之为“染色体”，在迭代计算过程中的数据更新变化则称之为“遗传操作”，通过不断迭代计算，整体的系统将收敛到一组固定值，这组固定值称之为“最佳染色体”，也即对应频率控制器参数的优化值。此时遗传算法结束，使用该算法获得的数值进行优化即可。

在应用遗传算法的过程中，其基本流程如下：①根据相应数据和未知量构建目标函数，将已知数据和未知量作为遗传算法的“染色体”，并考虑限定条件，将多个“染色体”统一构建为“初代种群”；②将“染色体”输入到系统频率响应综合模型中，以获得频率响应曲线，计算目标函数作为适应度；③留下满足约束条件的染色体，按照适应度的大小对其进行反复迭代计算，直至迭代计算结果收敛为止；④判断新的种群是否为末代种群，如不是则继续重复步骤③，直至新的种群属于末代种群后，输出相应数值，以达到优化参数的目的。

3 结语

总而言之，为确保实现对风力发电机组的优化控制，采用频率控制方法实现优化控制是一个较为可行的途径。对于频率控制而言，其关键在于减小频率变化和频率的偏差，并利用风电机组的快速功率调节能力加以实现。通过对风力发电机组频率的有效调节，有助于提升高比例新能源电力系统的运行稳定性，并为今后的电网升级改造提供理论支持。