案例教学在自回归模型教学中的应用

凌 云

（成都文理学院 四川·成都 610401）

0 前言

时间序列分析是统计学专业学生必修课程之一，在诸多领域都有着广泛的应用。自回归模型是时间序列分析的经典模型之一，强调其在实际中的应用，并将应用案例引入到日常教学中，将比较枯燥的数学模型与实践紧密结合，不但能加强学生对自回归模型的理解，丰富教学内容，扩大课堂信息量，而且能激发学生探索与学习的兴趣，提升学生的专业能力。本文通过自回归模型在人口预测中的应用，对案例教学在时间序列分析中的应用进行了粗略的探讨。

1 重要概念

构建AR(p)模型的步骤：

步骤1：对序列作平稳性检验，若经检验判定为非平稳，用平稳化方法将序列作平稳化处理；

步骤2：对平稳的序列作白噪声检验，若经检验判定序列为白噪声，建模结束；否则，转步骤3；

步骤3：对模型进行识别，估计其参数，转步骤4；

步骤4：检验模型的实用型，若估计的参数通过检验，残差为白噪声，则得到拟合模型并可以对序列作预测；否则转步骤3。

在步骤1中，判断一个时间序列是否平稳的最简单也是最直观的方法就是时序图法。将一个时间序列按时间顺序绘成连线图，若其始终在一个常数值上下随机波动，波动强度随时间变化不大，没有明显的趋势性和周期性，则认为该序列是平稳的。若序列不平稳，常用的平稳化方法有差分、趋势拟合、移动平均和指数平滑。

在步骤3中，通过自相关系数、偏自相关系数的截尾性与拖尾性作为模型识别的依据。若自相关系数拖尾，偏自相关系数p阶截尾，则可建立AR(p)模型。需要注意的是，如果识别出的不只一个模型，则需要根据AIC等准则来进行比较并选出最合适的模型。

在步骤4中，残差为白噪声是判断模型有效性的标准之一。时间序列分析的目的之一就是要将序列中的相关信息充分提取出来，一旦被充分提取，那么剩余的残差序列就应该是白噪声序列。

笔者在进行自回归模型的教学中发现，仅从理论的角度进行讲解，并不能引起学生的兴趣，同时使得学生难以用于实际问题中，不利于培养学生的专业能力。针对这个问题，结合自回归模型的广泛应用案例，在理论概念讲解之后，将其运用于实际问题——人口预测中，引导学生探索问题—收集数据—建立模型—预测，同时通过Eviews软件上机操作，加深学生对这部分知识的理解，培养学生的专业技能，提高教学效果。

2 案例分析

人口问题依然是目前世界普遍关心的重大问题之一。中国总人口数是指中国在某一时间点上的人口总数，人口众多、人均资源少依然是我国的基本国情，人口与经济、社会、资源和环境等各方面的不够协调仍是我国目前发展面临的重要问题之一。因而，利用数据探究我国人口总数的变化趋势、预测人口总量的变化，对与民生政策、经济政策、人与自然的和谐发展具有重要意义。本文根据上述理论，对1952-2018年中国总人口数序列进行分析。

2.1 中国总人口数序列的平稳性分析

对给定的时间序列，在建模时，序列应满足平稳性，故对1952-2018年中国总人口数序列作时序图进行观察，以此获得序列值的趋势和走向以及不同时刻序列值之间的相关关系。其时序图如下图1：

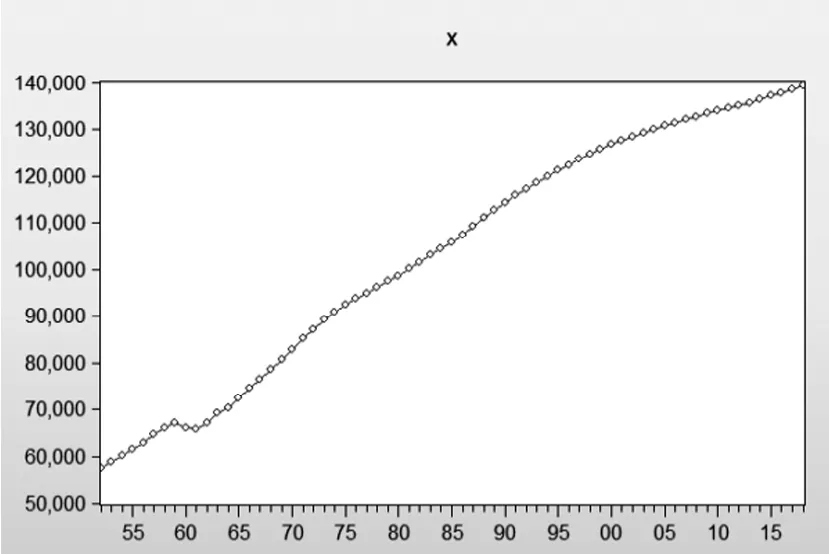
图1：1952-2018年中国总人口数时序图

由时序图可以得出，1952-2018年中国总人口数序列是非平稳的。于是，我们需要对该序列作平稳化处理。

1952-2018年中国总人口数序列有明显的线性增长趋势。因此可以考虑对该序列作一阶差分：

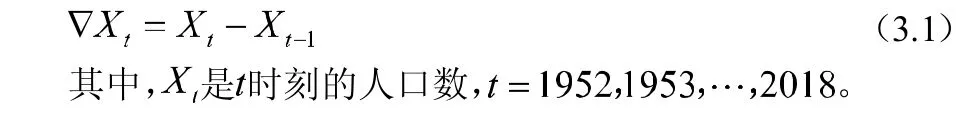
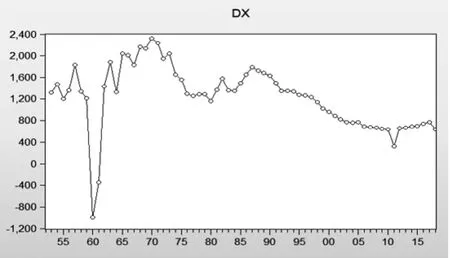
图2：1952-2018年中国总人口数一阶差分后的序列时序图

由时序图，该序列没有明显的趋势与周期，可以认为该序列是平稳的。

2.2 中国总人口数一阶差分后的序列的纯随机性检验

对给定的时间序列，在建模时，序列除了满足平稳性，还需要满足非白噪声。故对中国总人口数一阶差分后的序列作纯随机性检验，见图3。

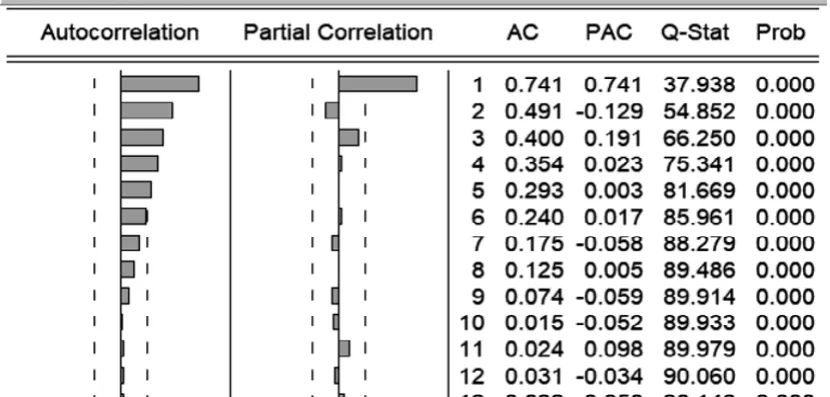
图3：一阶差分后的序列的纯随机性检验结果

由图3可知，在任意滞后阶数下，该序列的Q统计量检验的伴随概率均显著为0，因此拒绝其是纯随机序列的假设，可以认为该序列不是随机序列，满足序列是非白噪声的要求。可以对该序列建立时间序列模型。

2.3 构建模型

通过观察图3中的自相关系数、偏自相关系数，可以得出该序列的自相关系数拖尾，偏自相关系数1阶截尾，因此可以建立AR(1)模型。

图 4：AR（1）拟合相关参数图

构建的模型结果如下：

结果显示，AR(1)的p值小于0.05，通过了显著性检验。

通过残差序列进一步对模型的有效性作检验：

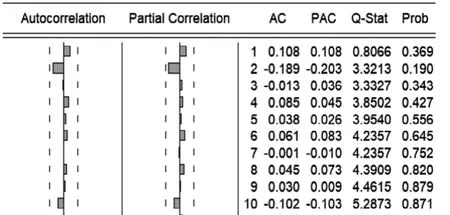
图5：AR（1）拟合残差的纯随机性检验结果

由图5可得，残差序列全部在二倍标准差的范围中，显示出良好的拟合效果。最后建立AR（1）模型如下：

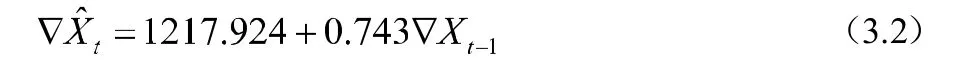
根据（3.1）与（3.2）建立我国1952-2018年总人口数的组合模型：

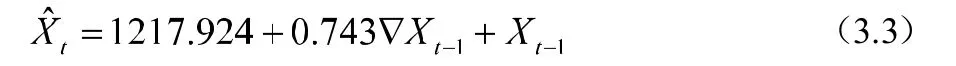
该组合模型的拟合效果是比较好的，见图6。

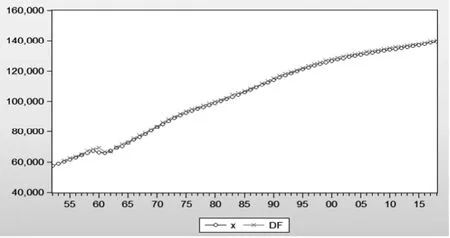
图6：组合模型的真实值x与拟合值DF的拟合效果

2.4 基于构建模型的人口预测

根据（3.3）式对2019年我国人口总数进行预测，预测值为140961.986万人。2019年我国人口总数的真实值为139772万人，真实值与预测值的相对误差为0.85%。该模型的预测效果是比较好的。

3 总结

自回归模型是时间序列分析的重要教学内容之一，其概念、性质和建模流程相对比较枯燥，教师仅从理论部分进行讲解，学生会难以与实际问题相联系。引入人口预测案例，通过Eviews软件上机实践，用完整的实际问题建模，能够帮助学生理解自回归模型的概念、应用及软件实现，更好的达到学以致用的目的。当然，自回归模型在实际中的的应用非常广泛，可引用的教学案例较多。例如，旅游人数预测问题、国内生产总值预测问题、气温预测问题等等。教师在教学过程中，可以选择更贴近学生学习基础，更能引起学生的兴趣的案例。同时，教师在将自回归模型用于人口预测中，可引导学生自主建模，完成探索问题—收集数据—建立模型—预测以及利用Eviews软件实现建模的过程，培养学生的专业能力。