浅析Matlab在线性代数教学中的应用

陈朝敏

（陆军步兵学院 江西·南昌 330100）

0 引言

线性代数是高等院校理工专业学生必修的一门重要的数学课程，其主要的数学工具，即矩阵理论，在众多领域都有应用。同时，线性代数也是学习其他课程的基础课程。近十几年来，随着我国信息化的不断深入，线性代数应用的广度和深度都有很大的提升，在这个大背景下，给线性代数的教学提出了更高的任务和要求，如何使学生在现有学时较少的条件下不仅掌握线性代数的系统知识，还能着重培养学生的代数思维和应用能力，成为新的教学研究方向。

线性代数具有基础概念多、理论逻辑性强、计算过程较繁琐等特点，但当前线性代数教学没有很好的平衡系统知识教学与案例式教学之间的关系，一是偏重于从数学问题到数学问题的解，教学实例较少，脱离实际应用背景；二是教学中涉及到的计算方法，如行列式计算、可逆矩阵求逆矩阵、求矩阵特征值和特征向量等，在低阶情况下，学生尚能接受，但对于高阶情况，手动计算显得较为困难，这导致线性代数较难应用于涉及高阶和复矩阵问题的后续课程，后果就是产生“数学无用论”的错误观点，无法提升学习的内动力，基于此研究现状，提出将Matlab应用于线性代数教学，论证对破解当前教学障碍、提升教学效果的可行性。

1 Matlab应用于线性代数教学的可行性

Matlab的产生与发展与计算机密不可分。1980年，美国计算机教授Cleve Moler在讲授线性代数时，为解决学生在高级语言编程上的难题，编写了Fortran子程序库接口程序，并命名为Matlab（取MatrixLabroary前三个字母，即矩阵实验室）。Matlab这一强大的科学计算软件越来越受到高校师生和广大科研人员的认可，在国内，部分高校也开设了Matlab相关课程。基于 Matlab强大的科学计算能力和图形处理功能，可以简化线性代数中涉及的复杂计算，对难以理解的概念通过可视化的方式加深理解，对线性代数的理解从感性认识提升到理性认识，培塑学生理论结合实际的素养，激发学习内动力。

2 Matlab应用于线性代数教学应注意的问题

Matlab应用于线性代数教学的益处不再赘述，但在运用中，需要考虑以下几个方面的问题：

（1）教学重点不能偏移。线性代数的“三个基本”仍是教学重点，只有掌握了系统全面的理论知识，才能更好的理解代数思维，Matlab只是辅助教学工具，不能将线性代数教学变成数学软件学习。

（2）适当补充必要的基础知识。Matlab的运用不止在第一课堂教学，更重要的是让学生在第二课堂利用Matlab解决学习中遇到的困难，所以应适当补充必要的软件基础知识，包括推荐整理Matlab学习资料给学有余力的学生，为接下来的数学建模竞赛打下良好的数学软件基础。

（3）针对学生的个体差异性设置不同难度的数学实验，Matlab应用于线性代数教学的最终目的是训练学生的代数思维与实操能力。因此，可根据学生的个体差异性设置不用难度的数学实验，并要求学生撰写实验报告，以检验教学效果。

3 Matlab应用于线性代数教学的具体探讨

在研究了线性代数课程地位、特点、教学现状、Matlab应用于线性代数教学的可行性和需要注意的问题后，就降低计算复杂度、显化概念理解、提升应用能力三个方面展开Matlab应用于线性代数教学的具体探讨。

3.1 功能强大的eig函数

矩阵特征值和特征向量在很多工程问题都有应用。根据特征值和特征向量的定义和性质，求矩阵A特征值和特征向量的方法如下：

因此，通过手工计算求高阶方阵的特征值和特征向量显得十分困难。正确的做法是在低阶情形下研究特征值和特征向量的性质，在此基础上，运用Matlab强大的数值计算能力简化高阶情形下的特征值和特征向量的求解。

Matlab提供了一个求矩阵特征值和特征向量的函数eig，其具体用法见下表1。

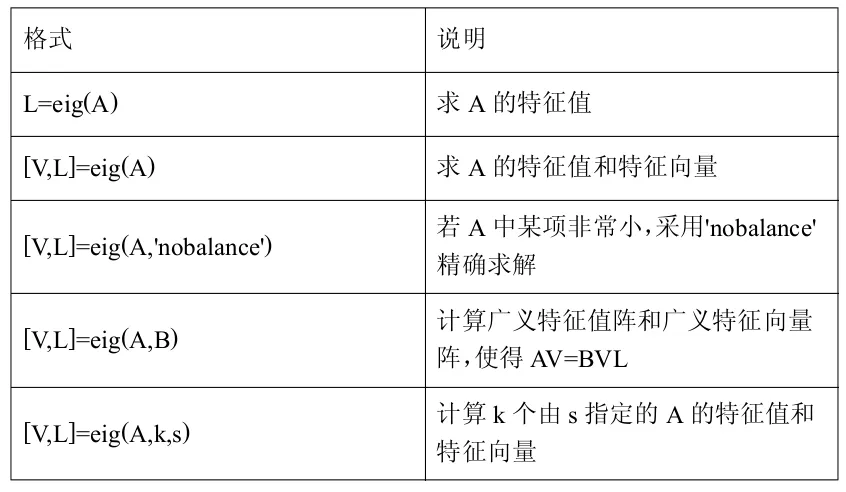
表1：eig函数的用法

3.2 可视化的力量

当前，教材中通常是利用坐标旋转变换介绍二次型这一知识点，这种从代数角度去理解二次型较为抽象，利用Matlab强大的可视化功能，采用数形结合的方法，将二次型以图形演示的方式展现出来，显化抽象概念，提升教学效果。

得到图形，如图1所示。

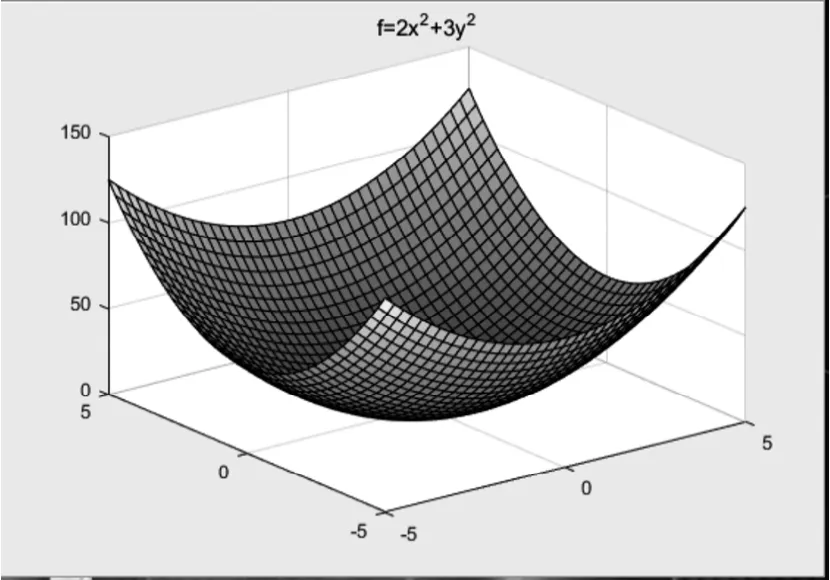
图1：正定二次型

由图1可知，正定二次型的图形都位于xoy平面上方。

3.3 矩阵运算的妙处

Leonado Fibonacci在其提出的兔子问题中引出斐波那契数列。与斐波那契数列有关的应用还包括著名的杨辉三角、黄金数等，那么该如何求出斐波那契数列的通项呢？

这里采用矩阵理论来研究斐波那契数列。

由斐波那契数列的定义和性质可得到如下差分方程组：

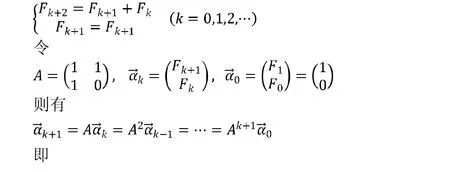
相比于运用矩阵对角化来求解要简便快捷，更能凸显线性代数的应用价值。

4 总结

本文主要就如何提升线性代数教学效果进行了研究，提出了将Matlab应用于线性代数教学的观点，并剖析了在具体运用实施时应注意的几个问题，最后就降低计算复杂度、显化概念理解、提升应用能力三个方面展开Matlab应用于线性代数教学的探讨。