基于Bisquare 算法的自适应数据采集策略

蒋明佑

(重庆交通大学机电与车辆工程学院)

传感器数据采集过程中，由于工业现场电器环境恶劣，不可避免的会产生量化噪声或随机噪声[1-8]。在噪声数据过多的采集任务中，离群数据[9]会影响一元线性回归模型的拟合过程，降低模型准确度。文章提出了基于Bisquare 算法的自适应数据采集方法，该方法根据数据点的离群程度，对每个数据点分配权值，通过权值分配降低噪声数据点产生的影响。通过迭代加权最小二乘法实时更新一元线性回归模型，大大提高了系统采集时间间隔的变化敏感度。通过设置模型置信区间，实现系统对噪声数据的剔除。文章使用LabVIEW[10]对基于Bisquare 方法的自适数据采集算法进行了仿真试验，并给出了基于Bisquare 方法的自适应数据采集和依托最小二乘法的自适应数据采集两者的性能比较结果。

1 数据设计

为了较为准确地模拟传感器采数据特性，文章基于LabVIEW 设计了幅值为5 的服从正态分布的最优数据源，每秒输出101 个数据点。将此数据源作为传感器所采集数据的最优数据源，如图1 所示。

最优数据源对应函数如下：

其中x 取值范围为[1，7]。

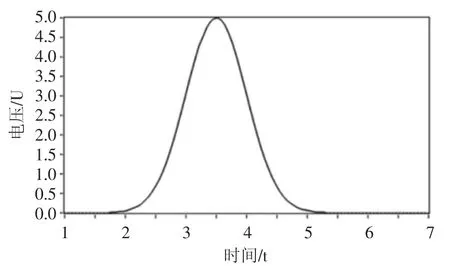
图1 最优数据源

通常采集测量任务中，大部分噪声均具有随机性，其幅度随时间无规律变化。为模拟真实传感器采集及数据传输时各种噪声对采集过程的影响，在原有最优数据源基础上添加了高斯白噪声及均匀白噪声。如图2所示。

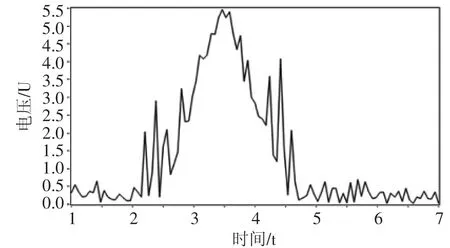
图2 添加噪声后的标准数据源

2 最小二乘法自适应采集

2.1 采集策略

基于最小二乘法的自适应数据采集的采集策略可分为两步：一，掌握数据变化情况。二，动态调整各个采集点之间的时间间隙。其中数据变化情况是系统结合有限个历史采样点，通过最小二乘法拟合一元线性回归模型来反应的。当数据发生变化时，对应的回归模型也相应发生变化。文章所提的依托最小二乘法的自适应采集中，通过拟合模型中斜率值的变化来调整采集时间间隔。

2.2 最小二乘法自适应采集工作原理

依托模型斜率调整采集时间间隔的最小二乘法自适应采集，其工作原理为：1）系统会结合有限个历史采样点，通过最小二乘法构建一元线性回归模型。

设有s1（x1，y1），（x2，y2）…sn（xn，yn）有限历史采样点，最小二乘法拟合如下：

通过上式得到了一元线性回归模型，将此过程迭代进行，获得实时变化的拟合模型，即通过模型掌握了数据变化情况。

图3 示出最小二乘法拟合模型与最佳信号源的对比效果。受噪声数据影响，在数据急剧变化时，模型拟合效果相对于最佳信号源具有一定偏差。这会导致系统在确定采集时间间隔时出现偏差，进而影响数据采集量，导致关键数据缺失。

图3 最小二乘法与最佳信号拟合模型对比效果

通过此方法，当拟合模型发生变化时，系统的采集时间间隔会根据所设区间发生变化，实现了自适应采集，效果如图4 所示。

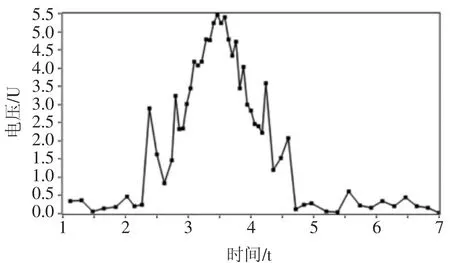
图4 最小二乘法自适应采集效果

从图4 可以看出，在区间[1，2]内，数据变化平稳，系统采集到5 个数据点。在区间[2，3]内，数据变化加快，系统采集到11 个数据点。在区间[3，4]内，数据变化最为剧烈，系统采集到17 个数据点。这表明依托最小二乘法，依靠拟合模型斜率调整采集时间间隔的系统具有自适应采集能力。但也可以看出在区间[2，3]和[4，5]内，由于系统对所有数据点等权重看待，所以即使采用变化时间间隔的采集方式也无法完全过滤掉噪声数据。

3 基于Bisquare 的自适应采集

3.1 采集策略

在掌握数据变化情况方面，此采集策略通过Bisquare[11]算法建立一元线性回归模型，由模型感知数据变化情况。Bisquare 方法在原有最小二乘法基础上为每个数据点分配了权重，其中赋予每个数据点的权重取决于该点距离拟合模型的距离，在拟合模型附近的数据点获得较高权重，远离拟合模型的数据点获得较低权重。通过Bisquare 算法很好的降低了噪声数据对拟合模型的影响，提高了模型准确度。此采集策略通过拟合模型斜率动态调整采集时间间隔，当斜率超过某个设定值时，系统调用对应的采集时间间隔。

3.2 噪声过滤

基于Bisquare 的自适应采实现了对离群噪声的过滤，原理如图5 所示。系统在已有的Bisquare 拟合模型基础上，在模型两端设置上下限，上下限阀值ε 可按需而定。当数据点落入区间以内时，如点s1，s2系统将按照指定采集时间间隔对数据点进行采集；对于落入区间以外的点，如点s3系统将不予采集。通过此方法，算法实现了对变时间间隔采集时离群噪声数据的过滤。

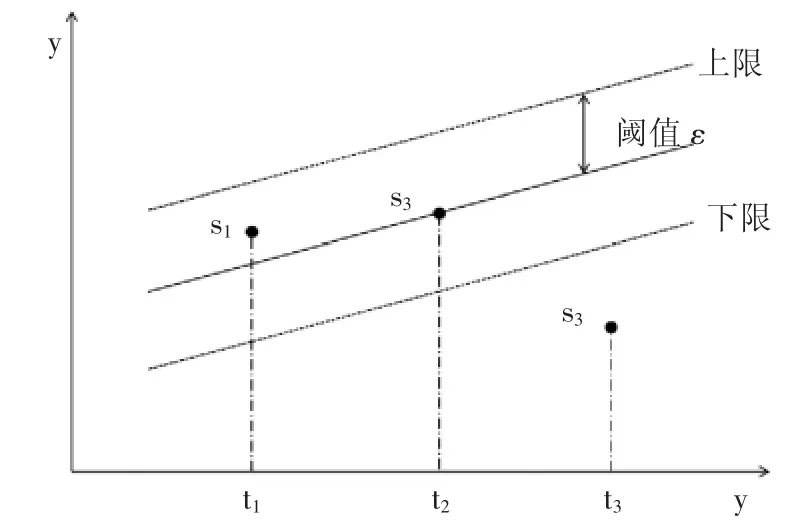
图5 噪声过滤原理

3.3 Bisquare 自适应采集工作原理

该算法首先通过最小二乘法对最近有限个离散数据点s2（x2，y2），（x1，y1）…sn（xn，yn）做线性拟合，得到最初拟合模型的斜率与截距的估计值ai与bi，其中i=0，n 为y 的长度。

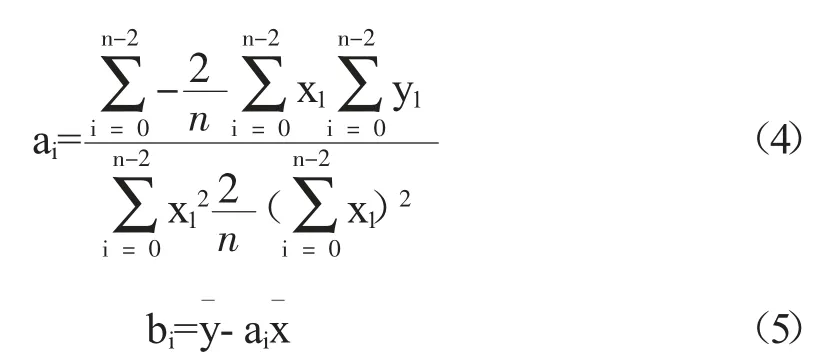
然后通过残差最小化的方法获得权重的更新值。Bisquare 算法的残差计算公式如下，其中wi为对应数据点的权重，fi为对应数据点的最佳拟合值。

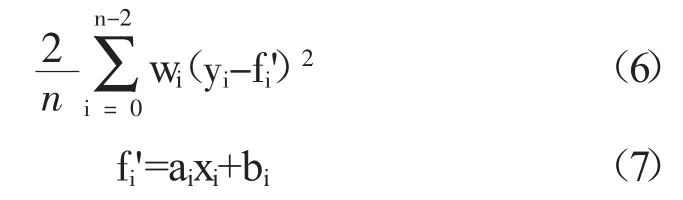
结合已知a0和b0，通过残差最小化，将上式对ai求导并等于零，可得。

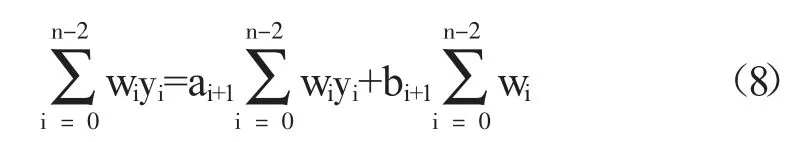
使用新获得的权重wi做加权最小二乘法，求得ai+2与bi+2：

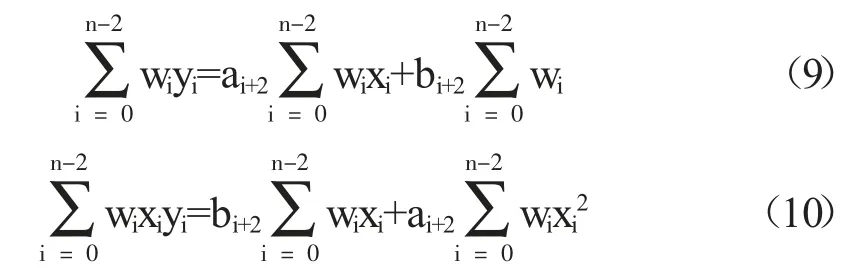
迭代以上过程，当迭代前后两次拟合多项式斜率与截距的相对差小于容差时，默认为获得最佳拟合模型，输出最佳拟合斜率，容差设置为0.000 1。

表1 斜率与采集时间间隔对应表

基于Bisquare 自适应采集时间间隔的确定流程，如图6 所示。

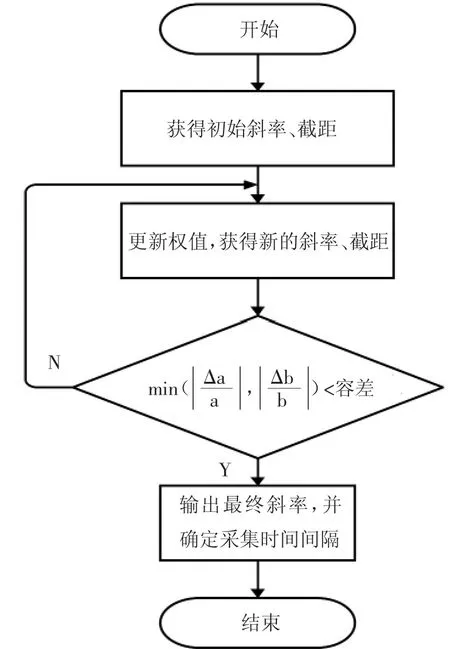
图6 采集时间间隔确定流程

获得最佳拟合模型后，系统根据最佳拟合模型斜率确定下次采集时时间间隔。在下次采集过程中，通过将最佳拟合模型上下限与标准数据源做差值处理，差值大于0 的点（即离群数据点）将被剔除。采集过程中离群点的确定，如图7 所示。

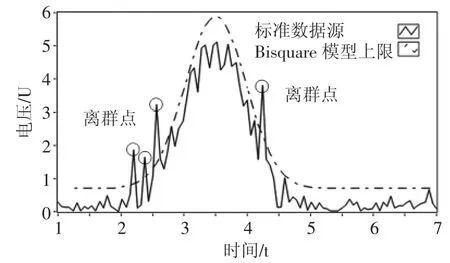
图7 离群点确定

图8示出Bisquare 拟合模型与最佳信号源的对比效果。Bisquare 算法很好的降低了噪声数据对拟合模型的影响。从图8 可以看出，Bisquare 拟合模型的数据走势与最佳信号源高度吻合，可以准确反映数据变化情况。

图8 Bisquare 拟合模型与最佳信号源拟合模型对比效果

通过基于Bisquare 的自适应采集方法，系统同样实现了具有自适应效果的变时间间隔采集，效果如图9所示。

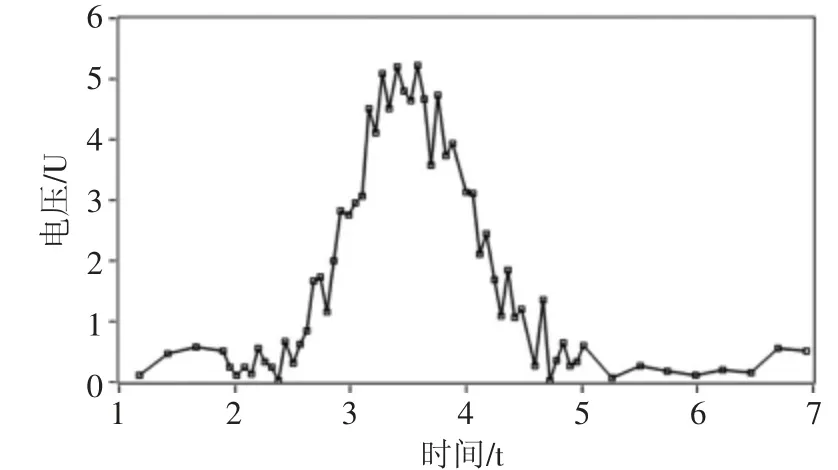
图9 Bisquare 自适应采集效果

从图9 可以看出，在区间[1，2]内，数据变化平稳，系统采集到5 个数据点。在区间[2，3]内，数据变化加快，系统采集到15 个数据点。在区间[3，4]内，数据变化最为剧烈，系统采集到17 个数据点。这表明基于Bisquare 算法，系统具有依照模型斜率调整采集时间间隔的能力。另外，系统过滤掉了离群噪声，所采集数据更加准确反应设备工况。

4 最小二乘法与基于Bisquare 的自适应采集性能比较

针对图2 提出的标准数据源，分别使用最小二乘法的自适应采集与基于Bisquare 算法的自适应采集进行试验。试验采集效果对比，如图4 和图9 所示。

其中，使用最小二乘法自适应采集工作60 s 后，系统保存3 240 个数据点，对比传统的等时间间隔采集，数据量降低了46%；使用基于Bisquare 的自适应采集工作60 s，系统保存3 840 个数据点，对比传统的等时间间隔采集，数据量降低了37%。

2 种采集方式都减少了数据量的存储，减缓了系统存储压力。但是最小二乘法自适应采集的数据存储量更低，这是由于拟合模型不准确造成的。受噪声数据影响，导致在[2，3]和[4，5]内，最小二乘法拟合模型斜率偏低，采集时间间隔增大，因此最小二乘法自适应采集相比于基于Bisquare 的自适应采集，所采集到的数据点更少。

最小二乘法自适应采集失真度相对较高。采用最小二乘法的拟合模型无法区分噪声数据，可以看到，图10 中有明显的离群噪声点。在噪声较多的数据区间，模型失真度较高。Bisquare 自适应采集通过权重分配的方法将离群噪声影响降到最低，所得拟合模型更加接近于最优数据源。模型对比效果，如图10 所示。

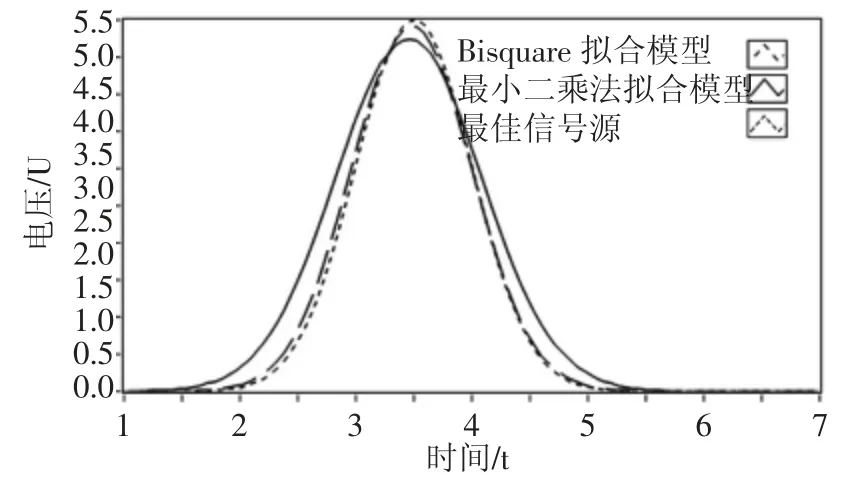
图10 最小二乘法与Bisquare 拟合模型对比效果

对于2 种方法的采集失真度，可以用2 种方法各自所得数据曲线fi'（x）与fi（x）最优数据源曲线之间所夹面积表示。失真度E（n）计算公式为：

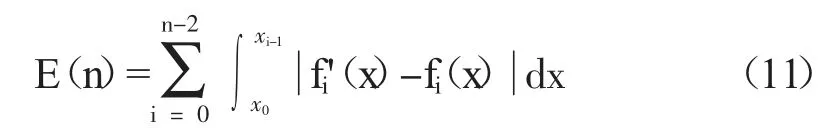
通过计算，同一时刻下，小二乘法的自适应采集的失真度为1.74，基于Bisquare 算法的自适应采集的失真度为1.21。需要说明的是，此试验的标准数据源时刻在发生变化，因此2 种采集方法的失真度也在变化。

在1 min 的采集试验内，基于Bisquare 算法的自适应采集平均每个数据点失真度比小二乘法的自适应采集失真度低0.34。

5 结论

文章提出了一种可以通过对数据点分配权重进而降低噪声影响的自适应采集方法。通过计算机仿真试验证明，在相同数据源的前提下，该方法在减少数据采集量的同时，可以更好地降低噪声数据对采集过程的影响，降低数据采集失真度。对比最小二乘法的自适应采集，该方法的失真度明显小于最小二乘法的自适应采集。通过采用此采集策略，数据采集失真度更小且数据存储量更低。后期可继续将Bisquare 算法进行优化，提高算法在无噪声条件下的应用效果。