巧用“数学步道”理念，培养数学模型思想

胡世娟

[摘 要]几何图形的公式教学一直是小学数学教学的难点。在几何图形的公式教学中，运用“数学步道”原理中的点数、目测、估算、分解组合等方法引导学生推导公式，可以把抽象的公式教学变得直观化、形象化，不仅放缓了教学坡度，而且降低了学生理解的门槛，同时也培养了学生的数学模型思想和探究创新意识，为小学数学几何公式教学开拓了新思路和新模式。

[关键词]数学步道;模型思想;圆的面积;案例;反思

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）08-0058-02

“数学步道”是指依托校园中的人行道、跑道、花坛等实物，运用步量、目测、测量、估算等一系列数学体验与活动，计算实物的长度、周长与面积的方法。运用“数学步道”原理推导几何图形的相关计算公式，可以化难为易、变抽象为直观，不仅可以锻炼学生的动手能力，提升学生的推理与归纳能力，而且可以培养学生的数学模型思想和探究创新意识，为学生的可持续发展打下良好的知识与技能基础。

[教学案例]

一、情境导入，启动思维

师：学校计划在新大楼前面建一个圆形花圃，如果让你设计花圃，该怎么做？

生1：需要先求花圃的面积，再根据面积算出需要多少花苗。

师：我们今天要探究的问题是圆的面积。

师：上节课，我们认识了圆并推导出圆的周长计算公式，谁能说说这个公式？

生2：圆的周长=π×直径=π×半径×2。

师：猜猜看，圆的面积会与周长公式中的哪些因素有关？

生3：与周长有关，周长越长圆的面积越大。

生4：与半径有关，半径越大圆的面积越大。

师：上节课我们已经证明了圆的周长与半径有关，因此，这几个同学的猜测可以归结为一种：圆的面积与半径的长短有关。下面我们一起做一个有趣的实验进行求证。

【设计意图：花坛是学生非常熟悉的事物，以学校建造新花坛为情境导入新课，可以激发学生的探究兴趣。让学生回顾圆的周长公式，一方面为探究新知做好知識铺垫，另一方面引出了实验探究活动。】

二、实验探究，验证猜想

1.教师演示

师（在黑板上画图，边演示边讲解）：我先画一个正方形，再以这个正方形的边长为半径画一个圆（如图1）;如果用数方格的方法，怎样算出这个圆的面积？（正方形中每个小格为1平方厘米）

生1：先数出1/4圆的面积，再乘以4，就得到这个圆的面积。

生2：先数整格的个数;接近整格的也算整格;其余不满整格的可以凑成整格。

（师生一起数方格，得出正方形的面积=16平方厘米;1/4圆的面积≈13平方厘米;圆的面积≈52平方厘米）

师：圆的面积大约是正方形面积的几倍？

生3（用计算器计算）：大约是正方形面积的3倍多一点。

师：圆的半径与正方形的边长有什么关系？

生4：圆的半径=正方形的边长。

师：正方形的面积=半径×半径。那么圆的面积呢？

生5：圆的面积=半径×半径×3=半径?×3。

师：从这个等式可以看出，圆的面积与半径的大小有关。

【设计意图：用数方格的方法计算圆的面积是运用了“数学步道”理念中点数、目测的方法（如用数砖块个数的方法计算人行道的面积）;接下来又用推理、数据分析等方法引导学生在圆的面积与半径之间建立关系。这样把直观教学和推理论证相结合，既拉近了学生与“真相”的距离，又为下一步学生的操作验证做好认知铺垫。】

2.学生操作

（1）学生画图

师：只用一个圆不足以验证猜想，下面每人拿出一张白纸，分别画两个边长为3厘米和5厘米的正方形，再分别以两个正方形的边长为半径画圆。

（2）数方格计算面积

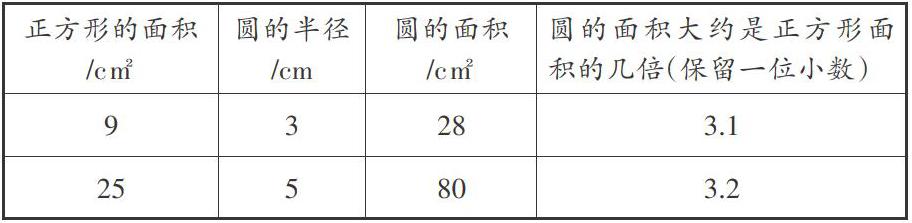
师：用老师发给你们的透明方格纸分别数出两个正方形的面积，填在表格里。

（3）完成表格

师：用计算器算出两个圆的面积，以及圆的面积是正方形的几倍，填在表格里。

（4）分析总结

师：从上面的表格中，你能发现圆的面积和它的半径有什么关系吗？

生1：圆的面积是它的半径平方的三倍多。

生2：圆的面积可能是π乘以半径的平方，因为π≈3.14，与3.1、3.2相近。

【设计意图：让学生自己动手操作验证猜想，不仅有利于培养学生的问题意识和探究精神，而且也为下一步推导圆的面积计算公式埋下伏笔。】

三、推导公式，建构模型

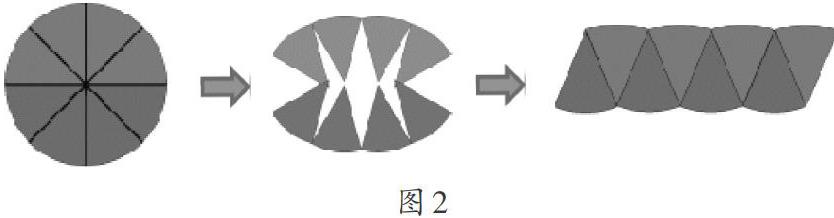
师：有同学提出“圆的面积=π×半径?”，到底是不是这样呢？我们仍需要通过实验进行验证。（教师演示把圆平均分成8份，并拼成新的图形，如图2）

师：把圆平均分成八份后拼成的图形像什么？

生1：像平行四边形。

师：请同学们拿出学具（事先画好的平均分成16份的圆），按老师刚才的方法，先把圆平均分成16份，再拼成一个新图形。

师：看看拼成的图形（如图3）像什么？

生2：像长方形。

师：如果把圆平均分成32份、64份、128份……用刚才的方法拼一拼，那么拼出的会是什么图形？

生3：会越来越接近长方形。

师：老师有一个妙招能让你们看到一直把圆平均分下去再拼出的图形。（动画演示）

师：拼成的长方形与原来的圆有什么关系？

生4：拼成的长方形的长是圆周长的一半，宽是圆的半径。

生5：长方形的面积=圆的面积。

师：如果圆的周长是C、半径是r，长方形的长和宽应怎样表示？面积怎样计算？

师（总結）：圆的面积公式该怎么写？

生7：圆的面积=长方形面积=πr?。

【设计意图：推导圆的面积计算公式是本节课的教学难点，这里运用“数学步道”原理中的分解、组合、目测、猜想等理念，引导学生通过实验操作、联想推理，全程参与公式的推导过程，亲自见证公式的“诞生”，验证了猜想的正确性，从而把圆的面积公式这一极为抽象的概念变得直观形象、具体可感。】

四、迁移运用，深化理解

师：如果花圃的半径是5米，它的面积怎样计算？

生1：S=πr?=3.14×5?。

师：计算圆的周长或面积时，有时因为计算过程比较复杂，也可以用含有π的式子表示计算结果，例如S=πr?=π×25=25π。

【设计意图：学生使用面积公式计算出花圃的面积，说明学生已经把公式内化吸收，并能运用公式解决实际问题，标志着学生已经圆满完成了对圆的面积公式这一概念的建构过程。】

[教学反思]

运用“数学步道”引导学生计算实物的长度、周长与面积，是一种非常“接地气”的数学综合实践活动。把“数学步道”理念应用于几何图形教学中，能够大大加快学生数学素养的发展进程。

1.化抽象为直观

公式教学一直是小学数学课堂教学的难点，运用“数学步道”原理中的点数、目测、估算、分解组合等方法，把公式的原理拆解成学生熟悉的生活经验和学习经验，让抽象的数学公式变得“接地气”，既是将抽象概念直观化的有效教学策略，也是培养学生数学模型思想的重要途径。

2.化繁为简、化难为易

应用“数学步道”理念进行公式推导，需要把探究过程分解成几步来完成，每一步通过实验、思考、推理、归纳等合作探究活动，完成一个层次，并提出下个层次的猜想，引出下一步的实验与探究。这样层层推进、步步深入，不仅放缓了教学坡度，而且降低了学生理解的门槛，让学生通过一步步实验操作验证猜想、推理论证，最终推导出计算公式，完成对公式模型的建构。

3.培养模型思想与探究精神

学生在公式推导过程中，必须眼、耳、手、脑并用，既要想象猜测又要操作验证;既要目测估算又要类比推理;既要分析数据又要归纳总结;既要合作探究又要交流讨论……这样，不仅锻炼了学生的实验操作能力，而且提升了学生的推理与归纳能力，同时也培养了学生的数学模型思想和探究创新意识，为学生的可持续发展打下良好的知识与技能基础。

（责编 罗 艳）