高中数学建模教学的探索

马云豪

[摘 要]数学建模素养是2017年版《普通高中数学课程标准》提出的六大数学核心素养之一.数學建模作为数学联系实际的重要桥梁，作为数学应用的重要表现形式，在数学教学中越来越受到重视.探索数学建模教学能有效提升学生的数学素养.

[关键词]数学建模;银行贷款;核心素养

[中图分类号]    G633.6        [文献标识码]    A        [文章编号]    1674-6058（2021）05-0009-02

一、数学建模于数学教育的意义

2017年版《普通高中数学课程标准》中，首次提出了数学学科的六大核心素养，数学建模在列.数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的素养.数学建模构建了“[提出问题→建立模型→解决问题]”的程序链.课程标准将数学建模的过程进行了细化解释：在实际情境中从数学的视角发现问题、提出问题，分析问题、建立模型，确定参数、计算求解，检验结果、改进模型，最终解决实际问题.

数学建模作为数学与实际生活的桥梁，及数学应用的主要形式，正日益受到重视.

二、数学建模教学案例

基于以上认识，笔者选择沪教版高一年级数列教学中的《银行贷款问题》做了初步尝试.

案例教学——银行中的数学.

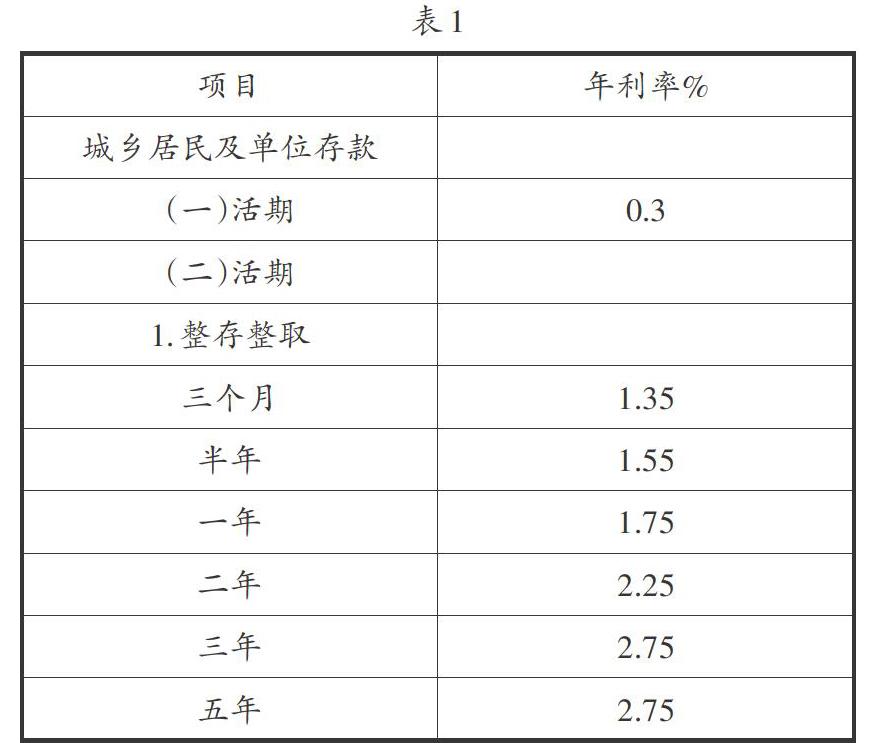
问题1：某银行利率如表1，现马老师向他人借了100万元，打算整存整取存入银行，

（1）按一年期定期储蓄，到期后共可获得多少钱？

[1 000 000×（1+1.75%）=1 017 500]（元）.

（2）按三年期定期储蓄，到期后共可获得多少钱？

[1 000 000×（1+2.75%）=1 027 500]（元）.

（3）按半年期定期储蓄，到期后共可获得多少钱？

[1 000 000×1+1.75%12×6=1 008 750]（元）.

设计问题1，以此来帮助学生复习存款问题，同时理解期数的概念，进而引入借贷问题.

问题2：马老师最近打算购置新房，打算向他人借取100万元，分期15年，逐月归还，请你帮他计算一下，每个月需要还多少钱？

[1 000 000÷180=50 0009]（元）.

问题2的设计是希望学生能够联系实际，发现问题，意识到在借贷问题中还需要考虑利息因素，从而引出银行贷款中的利率问题.

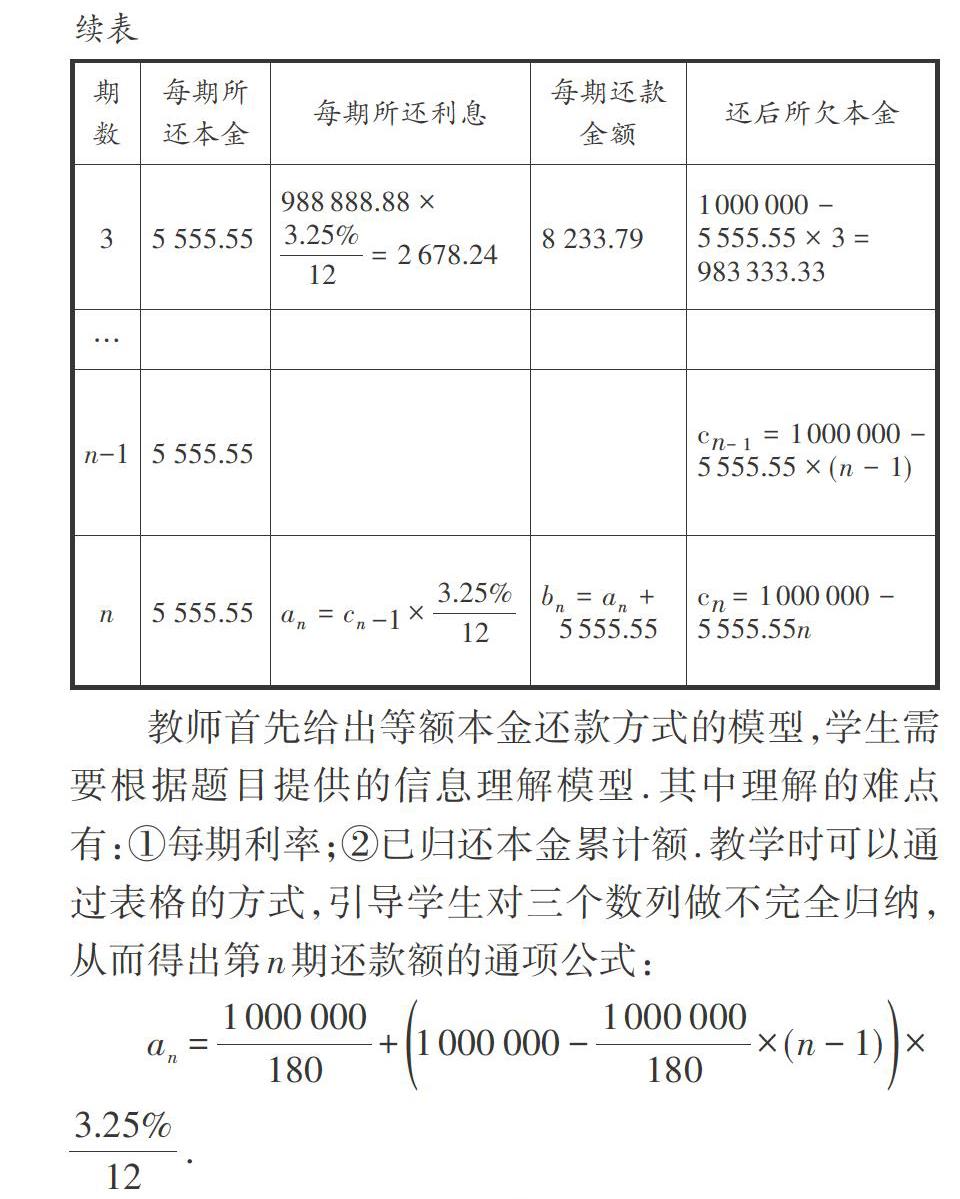
问题3：马老师计划向银行申请公积金贷款100万元，分期15年，共计180期归还，公积金贷款年化利率为3.25%.银行为马老师提供了一种等额本金的还款方式，既在还款期内把贷款数总额等分，每月偿还同等数额的本金和剩余贷款在该月所产生的利息.

每月还款金额= [贷款本金期数]+（本金-已归还本金累计额）×每期利率.

（1）马老师第一期需还款多少钱？

（2）马老师第三期需还款多少钱？

（3）马老师第n期需还款多少钱？

设数列[an]表示每期所还利息，数列[bn]表示每期还款金额，数列[cn]表示每期还款后所欠本金.

教师首先给出等额本金还款方式的模型，学生需要根据题目提供的信息理解模型.其中理解的难点有：①每期利率;②已归还本金累计额.教学时可以通过表格的方式，引导学生对三个数列做不完全归纳，从而得出第n期还款额的通项公式：

问题4：马老师每月工资为8 000元，无法承担等额本金前期的还款金额，已知公积金贷款最高贷款额为100万元，最长贷款年数为30年，贷款利率为3.25%，马老师依然计划申请公积金贷款，请你帮他设计一个贷款方案，每期需还款多少钱？

该问题的设计主要是希望学生体会到建模过程中如何确定和调整参数.

方案一：降低贷款总额，当贷款总额降低到96万元，首期还款为7 933.33元，之后逐期减少，马老师可以承担.

方案二：延长贷款年限，当贷款年限为30年时，首期还款为5 486.11元，之后逐期减少，马老师可以承担.

问题5：马老师依然觉得无法接受等额本金前期的还款金额，于是银行提出另一种还款方式，既等额本息还款方式：在还款期内，每期偿还同等数额的贷款（包括本金和利息），贷款的利息按复利计算.马老师依然计划申请公积金贷款100万元，分360期归还，公积金贷款利率为3.25%，则每期需还款多少钱？360期后总共还款多少钱？

问题5设计了生活中常用的等额本息的还款方式，是希望学生能从实际问题出发，分析问题，建立模型，从而解决实际问题.

在教学过程中，教师使用递推法来帮助学生理解问题5.对问题5部分参数进行改变，进而探求一般化情况.

设第n期还款后欠银行的本金为数列[an]，初始值[a0]元（即贷款金额），每期利率为[β]，总期数为m，每期需还款A元，则数列[an]满足递推公式：

三、对数学建模教学的反思

1.数学建模教学需要充分的铺垫.本课时原计划在一节课的时间内对等额本金和等额本息两种还款方式都让学生进行体验和探索.而学生对相关知识的很多背景材料都很陌生，需要教师进行解释，同时学生还需要对两种还款方式进行计算求解，能有充足的时间参与到数学建模活动中.因此，在实际教学中，可将本课时的内容拆分成两课时进行教学.因此，在数学建模教学过程中，对建模材料的铺垫必须要充分，教师需要对时间有足够的估计.

2.问题设计要与数学建模的环节有清晰的对应.教学设计中对问题的设计能对应到数学建模的某个环节，对数学建模活动进行分解，能针对某个环节进行训练.如本课时中，进行了如下设计.

3.参数调整能够有效地提升学生对建模的理解.如本课时问题4的设计，学生通过调整贷款总额和贷款年限进一步理解数学建模活动.实际上，数学建模是非常复杂的过程，数学建模教学需要区分与现有教学的区别.如果仅仅是面面俱到的教学，效果可能未必好.因此，建模教学可以仿照函数教学，对建模活动的每个环节进行分割，分步教学.

[   参   考   文   献   ]

[1]  中华人民共和国教育部.普通高中数学课程标准（2017年版）[S].北京：人民教育出版社，2018.

[2]  朱江红.等比累进还款法与等额累进还款法的数学模型[J].沧州师范学院学报，2017（2）：6-9.

（责任编辑 黄桂坚）