巧妙构造图形证明常见公式
2021-03-24李富国
中学教学参考·理科版 2021年2期
李富国

[摘 要]有些公式的证明比较简单,有些公式的证明有难度.如果换个方法,构造数学图形来证明,可以化繁为简.学习这种证明方法,可以开阔学生的视野.
[关键词]公式;构造;图形;证明
[中图分类号] G633.6 [文献标识码] A [文章编号] 1674-6058(2021)05-0003-02
从小学到中学,我们学过各种数学公式,有些公式记忆和推导起来比较容易,比如等差数列的通项公式,而有些公式的记忆和推导却比较困难,比如点到直线的距离公式.如果我们采用数形结合的方法,就可以比较直观地证明一些常见的数学公式.
先看一道小学竞赛题:
某日师父对他的徒弟说:我在你现在的这个年龄时,你只有2岁,等你到我的这个年龄时,我就41岁了,求师父与徒弟现在各多少岁.
这个问题可以利用一元一次方程来解,或者利用二元一次方程组来解,也可以不使用任何未知數,直接使用算术的方法来解,但是都没有下列图解法来得简单、巧妙.
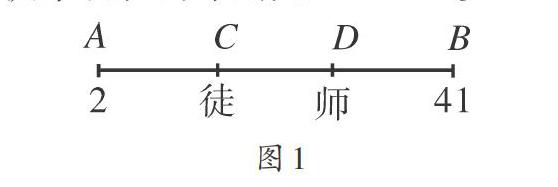
如图1,AB是一条线段,C、D是徒弟与师父现在的年龄的位置,当师父移到C时,徒弟移到A(2岁);当徒弟移至D时,师父移至B(41岁).可见,C、D是AB的三等分点,三段距离均为13.因此,师父现在为41-13=28岁,徒弟现在的年龄是2+13=15岁.
这真是妙解啊!“图解”的方便在于能直观、快速地看出问题的突破点所在,从而巧妙地解决问题.下面笔者利用图解法来证明常见公式.
一、证明均值不等式
两正数的算术平均值大于或等于其几何平均值,且取“=”的充要条件是两数相等.
从以上常见公式的证明可以看出,通过构造合理的图形能够把一些较复杂的公式化繁为简,起到事半功倍的效果.
(责任编辑 黄桂坚)