基于数学理解的游戏教学探析

2021-03-24沈君

中小学课堂教学研究 2021年2期

【摘要】数学理解是数学学习的重要过程与价值体现。它不仅包括“对数学的理解”，而且包括“数学化的理解”。数学理解具有自身发展跃迁的过程，将游戏环节与数学理解进行匹配设计，不仅符合学生的年龄特点，还能使学生在游戏沉浸体验中自然生发数学理解。

【关键词】数学理解;游戏教学;长方形;正方形

传统的学习中，通常把理解作为记忆的前提与手段;而当下，理解作为学习素养的有机组成已然成为教育的目的之一。数学理解是数学学习的关键，学生通过对数学知识、技能、概念和原理的理解与掌握来发展数学能力[1]。

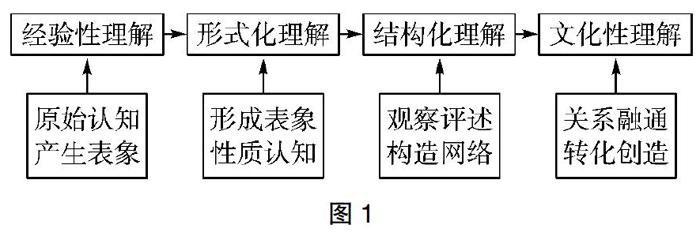
数学理解并不能一蹴而就，它是一个螺旋上升、不断跃迁的过程。首先，数学理解的出发点通常是原始认知、产生表象，即经验性理解;其次，经由形成表象与性质认知步入形式化理解;然后，通过观察评述与构造网络达到结构化理解，最后在知识的关系融通与转化创造中上升到文化性理解（如图1）。

基于此，笔者尝试将游戏教学与数学理解有机结合，以苏教版数学三年级上册“长方形和正方形”一课为例，通过游戏环节与数学理解的匹配设计，把游戏作为介质和干预工具，但又超越游戏本身，帮助学生学习，促进其数学理解[2]。

一、初玩游戏，在萌芽中产生认知表象

在小学低年级，学生已经认识点、直线、线段、角等几何元素，同时对长方形和正方形有了直观的认识，并初步积累了一定的图形探究活动经验。因此在长方形、正方形的二次认识与概念建立的过程中，教师可以利用游戏引导学生建立平面图形与现实生活的联结，明晰长方形、正方形与其他平面图形的区别，感受长方形和正方形的意义。

【环节1】谁是侦探小能手？

师：今天我们一起来做一回小侦探，找一找图片中有哪些不同的平面图形（教师展示相应的PPT）？

生：黑板的面是长方形。

生：卫生红旗的面是三角形。

生：课桌面是长方形。

生：凳子的面是正方形。

生：挂钟的面是圆形。

生：我发现教室的栏杆上有平行四边形。

（学生指着图片，屏幕上出现侦探柯南用放大镜寻找相应的平面图形。相应的图形从水平状态旋转为非水平状态，再逐渐复原。）

师：大家能将这些图形进行分类吗？

生：三角形一类，长方形、正方形和平行四边形一类，圆单独一类。

师：很好。其实像圆这样由曲线围成的图形，我们称它为曲线图形;像长方形、正方形和三角形这些图形，它们的边是直的，我们称它们为直线图形。今天，我们来研究最常见的直线图形——长方形和正方形。

数学理解是学生数学学习过程的中心环节，它一般是源于利用具体的材料、图形、符号等进行的数学活动[3]。在学生的原有认知中，实物与几何图形是没有关联的。因此，在教学的第一个环节，教师采用生活中的材料组成游戏元素，通过人人争做小侦探的游戏环节，激发学生学习的兴趣。在几何图形从物体的面上剥离的过程中，教师引导学生用数学的眼光观察生活中的物体，通过图形的不同位置，让学生形成视觉表象，关注几何图形的本质特征，并进行个性化分类。

二、放玩游戏，在探索中明晰图形特征

《义务教育数学课程标准（2011年版）》指出，学生学习应当是一个生动活泼的、主动的和富有个性的过程，学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程[4]。数学理解的积累离不开丰富的数学操作活动的支撑。因此在图形特征的探索阶段，可以采用学生喜欢的折纸游戏组织操作，使学生在图形特征获取的同时，感受图形的运动;在操作与思考中，体会变与不变的数学思想，收获丰富的活动经验。

【环节2】谁是折纸小达人？

师：长方形和正方形分别有哪些特征呢？

生：长方形的四个角都是直角，正方形的四条边长度相等。

师：怎么验证你的猜想？

生：用尺子测量它们的边，用直角三角板上的直角比画。

師：还有别的方法吗？

生：还可以把长方形和正方形折一折。

师：今天我们就一起来化身折纸小达人吧。请大家自由折纸，边折纸边画图，并记录操作过程与发现。

师：怎么折纸呢？有什么发现？

（学生上台演示对折，边折边说出长方形上下两条边长度相等，左右的两条边长度也相等。）

生：我补充，通过对折，我发现沿着折痕，长方形的上下两部分可以完全重合。

生：正方形通过对折也可以完全重合，而且它的四条边相等。

师：正方形还有什么特征吗？怎么证明它的四条边都相等呢？

生：我们可以把正方形斜着对折，这样它的四条边叠在一起，长度相等。

生：我把长方形也斜着折了一下，发现它横着的边比竖着的边长一些。

……

数学理解离不开操作与思考。在教学中，教师可以放慢教学速度，提出折纸游戏的要求，其目的是不仅让学生在自由轻松的氛围中经历操作与思考，利用个性化的折纸方式进行图形特征的体验与理解过程，而且让学生经历从猜想到验证，由质疑到辨析的数学思考过程。理解长方形和正方形的特征是如何得到的，这对于学生来说很重要，而学会从数学的角度看待、思考、解决现实问题更重要。这二者都是数学理解。

三、乐玩游戏，在辨析中建构概念网络

在教学中，通常希望学生得到的是关系性理解，但往往有时只是工具性理解。因此，游戏要关于数学本质做好充分的准备，其不是为了演示明显的数学特征，而是应该作为活动激发学生的数学理解和高阶认知。学生根据教师提示猜测图形的特征，既可以让学生巩固理解长方形和正方形的特征，又可以巧妙地引出长方形和正方形的关系网络。

【环节3】谁是推理小高手？

游戏规则：教师取出信封1，告诉学生里面装了一些四边形，让学生根据提示猜一猜是不是长方形或者正方形。

师：这个四边形对边相等，是什么图形？

生：长方形。

生：不一定，也许是正方形。

师：你们猜得对不对呢？瞧，这个四边形偷偷地露出了一个角（如图2）。

师：大家还猜它是长方形或者正方形吗？

（教师随后抽出图形，发现其实这是一个平行四边形。）

师：咦，这个图形明明就是对边相等的呀，为什么它不是长方形呢？

生：我明白了，判断一个图形是不是长方形，既要看它的边，也要看它的角。

师：信封2里也有一个四边形，这个四边形有4个直角，猜猜看是什么图形？

生：可能是长方形或者正方形。

师：怎么没有人猜别的图形呢？

生：有四个直角的四边形要么是长方形，要么是正方形。

[教师从信封2中抽出一个长、宽比较接近的长方形（如图3）。]

师：看，这是什么图形呀？

（学生众说纷纭。）

生：这是正方形。

生：不对，这是长方形。

生：我觉得说是长方形肯定没错。因为正方形的对边相等，4个角也都是直角，所以即使是正方形，也可以说它是长方形、一种特殊的长方形。

这个游戏环节不仅富有童趣，而且能够发展学生的空间想象能力。学生在游戏中思考，将语言转化为头脑中具体的图形表象，经过对比图形特征与条件提示，进行思考与判断。在逐渐质疑与辨析中，学生发现正方形其实是特殊的长方形，建构了概念的知识网络。当学生以概念同化的方式将正方形纳入长方形系统中，本质上就是数学理解的发生。

四、慧玩游戏，在转化中理解图形变化

在实际教学中，如何从一个长方形中折出或画出一个最大的正方形，是学生较难理解的问题。因此，在环节3猜测图形的游戏后，教师马上预设了环节4的游戏，让学生在质疑中自己动手验证信封中抽出的究竟是长方形还是正方形。

【环节4】谁是百变创意家？

师：这到底是长方形还是正方形呢？怎么验证？

生：可以通过折一折验证，这是一个长方形。

师：为什么确定是长方形了？

生：因为它的四条边不一样长。

师：谁来当百变创意家，把它变成一个最大的正方形？

生：在刚刚折好的图形中，把多余的裁掉。

师：很棒，这样我们就把这个长方形变成了一个最大的正方形。

生：我突然想到了把正方形变成两个相同长方形的方法。从中间把它直直地分开就可以了。

通过游戏方式，学生被引入了图形变化的思考情境中。环节4的游戏设计与前面的游戏密不可分，是建立在放玩游戏的基础上的。当学生有了充分的操作活动体验后，学生自然地由长方形的长和宽的比较中发现了二者之间互相转化的渠道。