巧探古今生活，浸润数学文化

王进敬　余庆纯

【摘要】在“锐角的三角比的意义”课例教学中，研究者将校园生活中的“不可测问题”转化为数学问题，基于多元视角探索不同的解决方案，从一般三角形的全等、相似到直角三角形的相似，自然引出锐角三角比，揭示锐角三角比学习的必要性;借助古代的特色计时工具日晷进行古今对照，揭示锐角三角比、锐角三角函数等初高中相关数学知识和方法的共性，突出学习锐角三角比的重要性。实践表明，“锐角的三角比的意义”教学浸润知识源流、学科联系、社会角色、审美娱乐、多元文化等维度的数学文化，深刻地揭示了数学史的六类教育价值。

【关键词】锐角的三角比;正切;余切;数学史;数学文化

基于数学史的数学文化，可以划分为知识源流、学科联系、社会角色、审美娱乐与多元文化五个维度。但有研究表明，数学文化的五个维度在教学实践中运用并不均衡[1]，因此，在教学中，教师需立足教育现实，挖掘数学史素材，优化课例教学。

“锐角的三角比的意义”是沪教版数学教科书九年级上册第二十五章第一节的内容。《上海市中小学数学课程标准（试行稿）》在“学习内容与要求”中指出，要利用直角三角形定义的锐角三角比，建立直角三角形中边与角的联系，它是定量地研究三角形的基本工具。在锐角三角比的学习中，注重概念的理解[2]。经过实践研究发现，“锐角的三角比的意义”教学大多从直角三角形的相似入手，通过寻找规律，得出锐角三角比的定义。在沪教版教科书的“设计说明”中也明确提出，在三角形及相似三角形中，主要从定性方面研究三角形（或两个三角形）的特征与性质;在锐角三角比中，主要从定量方面研究直角三角形。锐角三角比的概念是三角函数概念的基础。然而，在沪教版教科书中，其以正切为切入点，利用梯子的倾斜程度、测量金字塔的高度为背景引出锐角三角比，并未真正揭示三角比与一般相似三角形的根本联系，没有揭示学习锐角三角比概念的必要性。

鉴于此，本研究从学生熟悉的校园场景入手，设计一系列“不可测问题”，借鉴20世纪上、中叶英美教科书中的锐角三角函数的引入方式，选择性地进行教学重构，在分析问题、解决问题的过程中追本溯源，突出锐角三角比学习的必要性和重要性。

基于HPM视角，拟订“锐角的三角比的意义”的教学目标如下。

（1）经历锐角三角比概念的形成过程，经历将校园生活中“不可测问题”转化为数学问题，再抽象出数学概念的过程，学会抓住事物的本质属性。

（2）掌握锐角三角比的概念，能根据直角三角形中两边的长，求解锐角三角比的值。

（3）在概念形成的探究过程中，体会初中和高中数学内容、数学与其他学科、数学与生活之间的紧密联系，培育善于思考、严谨求实的理性精神，增强“学数学、用数学”的实用数学观，欣赏多元的数学文化。

一、史料运用

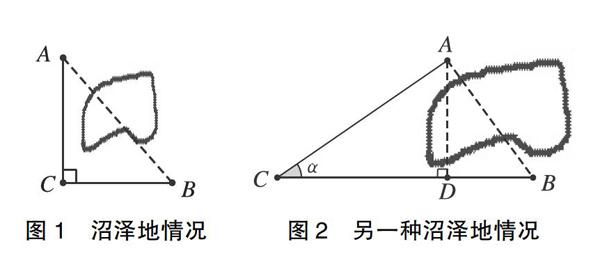
20世纪上、中叶美英教科书中，已有锐角三角函数丰富的引入方式。其中，有一个“水管求长”的生活情境：假设A地为水源，B为房屋，A、B之间以一片沼泽地分隔开来，现要用一根水管将A处的水流引到B处，问需要多长的水管（即计算AB的长度）。若沼泽地的位置相对特殊（如图1），则能够找到一点C，使得∠ACB=90°，且AC、BC的长度均易于测量。通过测量AC、BC的长度，运用勾股定理可得出AB的长度。但若沼泽地的位置相对一般（如图2），因无法直接找到点C使得∠ACB=90°，则需要通过构造直角三角形的方式，测出AC和BC的长度以及∠ACB的度数，若能求得图中AD和CD的长度，即可求出AB的长度[3]。于是，可以得到“已知直角三角形的斜边和一个锐角，可求出直角边”的解决方法。

日晷是中国古代经典的计时器物之一，其是锐角三角比运用于社会生产、生活中的重要体现。为了研究日晷如何记录节气、测量，假设点S表示太阳，GN为日晷的晷针，AN为正午的晷影（如图3），记录每天正午的晷影长度。一年中，晷影长度最长的那一天是冬至，晷影长度最短的那一天就是夏至。当晷影长度达到最长之后，逐日变短，直到最短，然后又逐日变长，直到最长，共经历一个完整的回归年。观察Rt△ANG，在∠A不变的情况下，当晷影AN由长变短，∠A的对边与邻边、邻边与对边之比是固定的;当∠A变大时，∠A的对边与邻边的比值GN/AN变大;当∠A变小时，比值GN/AN变小，即∠A的对边与邻边的比值随∠A的变化而变化（如图3）。

在我国许多地方，保存着相对完整的古代日晷，比如北京故宫的日晷、江苏常州天宁寺的日晷，以及复旦大学和上海交通大学等校园里的日晷等。依据晷面摆放的位置、角度与使用地区的不同，古代日晷常分成多种不同的类型，其应用范围也不尽相同。按照晷面摆放的位置进行分类，可分为赤道式、地平式、垂直式三类日晷。

（1）赤道式日晷（如图4），又称为斜晷，其晷面与赤道面平行，晷针平行于地球自转轴且两端分别指向天北极（北极星）、天南极，晷针与平坦地面所形成的角度代表当地的地理纬度，如北京故宫的日晷就是赤道式日晷。

（2）地平式日晷（如图5），其晷面与平坦地面相互平行，晷针分别指向天北极（北极星）与天南极，晷针与晷面之间的夹角代表当地的地理纬度。在北京故宫博物院里，收藏着清朝顺治年间的一个新法地平日晷。其晷面上分别刻着时刻线、节气线;晷针是可起落的三角形晷针;靠近晷针的一侧安放着一个指南针，便于测定方向。

（3）垂直式日晷（如图6），又称为立晷或竖晷，其晷盘面垂直于平坦的地平面。大多数垂直式日晷安置在房屋的墙壁、石碑等建筑物向阳的竖直方位上，如江苏常州天宁寺的垂直式日晷（又称为面东西日晷），其是清代阳湖（今常州武進）知县张作楠所制。此外，在欧洲许多国家的建筑外墙上，常常会附建有各式各样、颜色各异的垂直式日晷。

鉴于此，基于20世纪早期美英教科书中锐角三角函数的引入方式，创设“不可测问题”情境，借助相似三角形的相似比进行深入探究，引入锐角三角比的概念，借助古代的特色计时工具日晷进行古今对照，自然地揭示锐角三角比从静态到动态变化过程中所蕴含的函数思想本质，突出学习锐角三角比的重要价值，感悟数学源于生活，服务于生活的社会角色，揭示数学与天文学之间的学科联系，展现数学文化之魅。

（五）课堂小结

本节课建构了三角形边与角的转化桥梁，学生学习了正切、余切等锐角三角比，根据直角三角形中两边的长求解锐角三角比的值，感悟初中和高中数学内容、数学与其他学科、数学与生活之间的紧密联系。

三、学生反馈

课后，教师对两个教学班的61名学生进行问卷调查，调查结果如下。

1.本节课中，你印象最深的环节是什么？为什么？

大部分学生对锐角三角比的引入过程印象深刻（如图18），其原因有三个方面：第一，传统课堂大部分采用“输入—被动接受”的学习方式，缺乏知识探究的过程，不能很好地解答学习锐角三角比的必要性，而本节课以校园中“不可测问题”的探究，引入锐角三角比，重构式地展现了对锐角三角比的思考和探究过程。第二，以校园实际问题为例，将现实问题抽象成数学问题，运用所学的数学知识进行分析问题、解决问题，真正做到学以致用。随着问题条件越来越一般化，难度越来越大，对知识的灵活运用程度也越来越高，不仅具有挑战性，而且需要触类旁通，并建构体系化的知识网络。第三，很多学生表示喜欢探究式学习的氛围，在分析问题、解决问题过程中与同学进行多次互动，使得探究式学习富有生机活力。

还有一些学生表示对介绍日晷的视频印象深刻，其原因主要是日晷与所学的锐角三角比的知识联系紧密，激发了其学习兴趣与动力，使其体会到数学源于生活，服务于生活;还有的学生觉得教师制作的微视频条理清晰，有理有据，与学习内容很贴切，有力地论述了古人设计日晷时的高超智慧。

2.在日后旅游或参观时，是否会更加关注日晷？为什么？

在问卷调查中，大部分学生表示会更加关注日晷，其主要原因是理解了日晷的实践运用与数学本质的联系，激发其深入探究的学习兴趣。其次，对于现在的学生，电子手表是他们日常的计时工具，而日晷这一古老的计时工具是如何工作的、日晷与电子手表相比哪个更加准确等问题，激发了学生的学习兴趣与求知欲望。此外，有一部分学生还提到以前很困惑日晷的计时原理，现在终于解开谜团，深刻感受到数学与生活的紧密联系。

四、文化分析

“锐角的三角比的意义”课例教学以史为源，古为今用，重构式地融入知识源流、学科联系、社会角色、审美娱乐、多元文化等，浸润数学文化的芬芳。

（1）知识源流。借鉴20世纪上、中叶英美教科书中的锐角三角函数的引入方式，选择性地进行教学重构，以校园生活为背景，引导学生基于不同实际情境，探究系列“不可测问题”的解决方法，在分析问题、解决问题的过程中掌握锐角三角比的概念定义，学会根据直角三角形中两边的长求解锐角三角比的值，揭示学习锐角三角比的必要性。锐角三角比不仅探析了三角形角度与边的比值关系，而且为学生今后学习三角函数奠定了基础。

（2）学科联系。锐角三角比是天文观测、航海测量等跨学科内容的基础，能助力学生进行跨学科知识的学习与方法运用。

（3）社会角色。以微视频的形式展现日晷与锐角三角比的密切联系，突出锐角三角比在社会生活中的实际运用，展现数学源于生活、服务于生活的重要角色。

（4）审美娱乐。正切、余切等锐角三角比，定量地刻画了直角三角形中锐角的角度与两直角边长度之间的紧密联系，突出数学的简洁美、统一美。

（5）多元文化。基于20世纪早期英美教科书，创设校园生活中“不可测问题”的活动探究，引出锐角三角比的概念;再以日晷介绍古代人们运用锐角三角比的知识，制作日晷来测量时间、记录节气等，古为今用，洋为中用，展现多元数学文化的交融。

五、教学反思

“锐角的三角比的意义”课例教学揭示了数学史的六类教育价值。

（1）知识之谐。全等三角形、相似三角形主要从定性的角度研究了三角形的性质，而锐角三角比主要从定量的角度研究了三角形中边与角的数量关系，奠定了锐角三角函数的学习基础。借鉴20世纪早期美英教科书中的锐角三角函数的引入方式，设计校园“不可测问题”的学习活动，通过构造全等三角形、借助中位线或平行线等构造相似三角形等方式来分析问题、解决问题，体现了锐角三角比与相似三角形（包括全等三角形）的本质联系，突出学习锐角三角比的必要性;正切、余切等锐角三角比随着锐角的变化而变化，有助于理解锐角三角比是三角函数的雏形，体现知识之谐。

（2）方法之美。在“不可测问题”的解决过程中，展现了从一般到特殊的演绎推理（从一般三角形的相似到直角三角形的相似）与从特殊到一般的类比推理（从解直角三角形到解一般三角形）等数学思想方法的有机统一，培养学生有逻辑、有条理地分析问题、解决问题，揭示方法之美。

（3）探究之乐。通过活动探究，从多维角度将校园“不可测问题”转化为“可测问题”进行深度分析，经历知识发生、发展的过程。发现当直角三角形中的锐角固定时，锐角α的对边锐角α的邻边是一个定值;当直角三角形中的锐角变化时，锐角α的对边锐角α的邻边比值也随之变化，滲透函数思想，积累数学活动经验，品味探究乐趣。

（4）能力之助。借助校园生活中的“不可测问题”情境，培养学生学会从不同的数学知识领域来分析问题、解决问题，这是综合运用数字知识、技能、思想方法等进行数学抽象与逻辑推理（数学化）的过程。这不仅有助于培育学生进行数学表达与交流，发展问题解决能力，而且有效地提升了学生数学抽象、逻辑推理、数学建模等数学学科核心素养。

（5）文化之魅。基于20世纪美英教科书中的锐角三角函数引入方式，展现中西方多元文化的交融。其次，通过播放微视频，介绍江苏常州天宁寺、复旦大学和上海交通大学等地的日晷，揭示锐角三角比在中国古代传统计时器具日晷中的应用价值，贯古连今，传承中国优秀的传统文化。

（6）德育之效。情感方面，以“不可测问题”情境引导学生亲近数学、发现数学、探究数学，引发学生学习动机，激起学习兴趣;理性方面，综合运用数学知识、方法等来分析、解决“不可测问题”，培育学生善于思考、严谨求实的理性精神;信念方面，引导探索日晷背后的数学本质与人文故事，增强文化自信。

参考文献：

[1]余庆纯，汪晓勤.基于数学史的数学文化内涵实证研究[J].数学教育学报，2020（3）：68-74.

[2]上海市教育委员会.上海市中小学数学课程标准（试行稿）[M].上海：上海教育出版社，2004.

[3]卢成娴，汪晓勤.20世纪上、中叶美英教科书中的锐角三角函数引入方式[J].中学数学月刊，2019（2）：45-48.

（责任编辑：陆顺演）

【作者简介】王进敬，高级教师，上海市数学教育教学研究基地HPM工作室骨干成员;余庆纯，华东师范大学数学科学学院在读博士研究生，主要从事数学史与数学教育研究。

【基金项目】上海高校“立德树人”人文社会科学重点研究基地之数学教育教学研究基地研究项目——数学课程与教学中落实立德树人根本任务的研究（A8）