弄清等号的意义，让学生的代数思维更成熟

2021-03-24王小云

小学教学参考(数学) 2021年3期

王小云

[摘要]学生初学等号，了解它是用来连接两个等值的数，表示相等关系。在后续学习算术时，等号功能发生转变，作用变成标记计算结果。教学时要遵循学生认知的发展演变规律，选择时机来引导学生理解等号表示大小相等关系的功能。这样有利于学生理解代数关系式。

[关键词]代数关系式;加法;启蒙 ;数形结合

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）08-0022-02

义务教育阶段的数学知识的连贯性越来越强，小学算术与初中代数之间的“代沟”几乎弥合。新版小学教材中，一些带有“代数启蒙隐喻”的题目开始出现，如苏教版教材第一册第71页第9题（如图1）。

某位教师讲解这个问题时指导学生利用代数关系式“a+b=（a+1）+（b-1）”来解答第一个算式，但学生自主完成其他算式时状况频发：有的学生在填写第二个算式时想到6+1=7，于是在左端方框填入1，右端方框则随意填写;有的学生觉得一个等式中等号两边的方框里应填同一个数，左式是6+3，右式则是7+3;有的学生做对了，但他们是先自定左式的得数，再去推算右式中应填入什么数才得到这个得数。按照教师教授的方法做题且做对的学生仅有2名。

从上述情况来看，问题有二：其一，学生对等号意义的理解不透彻;其二，学生不理解代数关系式“a+b=（a+1）+（b-1）”。如何让学生在接触这道题前做好思想准备和知识铺垫？

一、多维度建构，理解等号的意义

在学生学习了“等号表示大小相等关系”之后进行巩固练习，让学生加深对等号这一功能的理解。如教学苏教版教材第一册第51页第5题（如图2）：

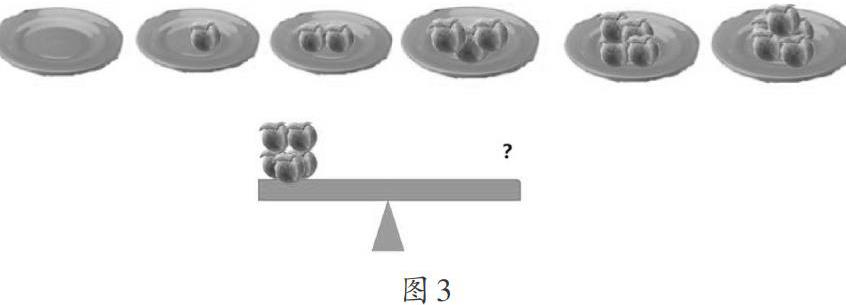
师（出示图3）：每个桃子一样重，要使天平平衡，右端可以放哪两盘中的桃子？

生1：1个桃子和4个桃子这两盘。

师：为什么？

生1：天平左端有5个桃子，右端也应放5个，天平左右两端桃子质量相等，才能平衡。

师：左端放有5个桃子用“5”表示，右端放4个桃子和1个桃子，怎么用数学算式表示？

生2：用“4+1”或者“1+4”表示。

师：此时，天平两端桃子的个数都是5，天平平衡，怎么用数学算式表示这种平衡关系？

生3：有两个算式可供参考，5=4+1或5=1+4。

师：真聪明！还有别的摆法吗？你们能够边摆桃子边解说吗？（学生上台演示并写出算式：5=2+3;5=3+2;5=5+0;5=0+5）

师：这些算式和以往学的算式有什么区别？

生4：以往学的算式，加法运算在左边，得数在右边，现在刚好颠倒过来。

师：你发现等号两边的算式和得数互换位置了。

生5：如果换回来还是和原来一样。

生6：就像天平两端的重物交换位置，天平仍然保持平衡。

师：联想到天平两端的重物交换位置，真棒。

（教师板书算式）

师：比较上面两组算式，它们有什么共同点？

生7：加法运算的计算结果都是5。

生8：中间都是用等号连接的。

生9：左边这组算式，数字5在左端，算式在右端，两边的值相等;右边这组算式，算式在左端，数字5在右端，两边的值相等。

师：以往我们习惯把算式写在等号左端，得数写在等号右端，现在算式和得数刚好调换位置，但是两边始终相等，所以中间一直用等号连接。

上述教学过程中，教师利用天平的平衡原理来类比等式的相等关系，并概括出等式，让学生把抽象的“等号的关系性质”融入具体的天平平衡中。在新旧算式的对比中，学生自觉应用“等式性质”改变原有对算式的狭隘认知，通过调换位置，把等号的功能从“表示计算结果”转向“表示相等关系”，加深对等号“表示相等关系”的理解。

二、动手操作，初步感知

学生在解决图1中的问题时，要用到“a+b=（a+1）+（b-1）”这个代数关系式，所以必须深入理解它。在“代数思想启蒙”阶段，并不需要学生将题目中隐含的代数关系提炼出来，但是学生要对这个代数关系有一个初步感知、大致理解和简单应用的过程，能够用自己的方式来理解和运用它，形成代数关系的意识，这样才有可能运用上述的代数关系式来解题。

动手操作是学生理解运算符号意义的最佳手段，同时也是理解算式数量关系的最佳途径，学生对于“a+b=（a+1）+（b-1）”这个代数关系式的理解也应从动手操作开始。如教学苏教版教材第一册第13页第2题（如图4）：

（讓学生先根据指定的数目给圆圈着色，然后观察结果，说说自己的发现）

生1：涂色圆圈的个数依次是2、3、4，空白圆圈的个数就是3、2、1。

生2：涂色圆圈每次增加1个。

生3：空白圆圈一个个减少。

生4：涂色圆圈每次增加1个，空白圆圈每次减少1个。

师：这是为什么？

生5：总共5个圆圈，涂色圆圈每增加1个，空白圆圈的数量自然就会相应减少1个。

师：没错。5个圆圈总数不变，涂色圆圈每增加1个，空白圆圈就会减少1个。

上述教学过程中，在涂色之后交流研究，学生的注意力从按照指定数量涂色，转移到涂色圆圈与剩下的空白圆圈之间的数量对应关系上，学生根据操作中的现象来描述这种数量变化关系，形成对“a+b=（a+1）+（b-1）”这个代数关系式的初步感知和印象。

三、数形结合，多元表征

在前面的学习中，学生对“a+b=（a+1）+（b-1）”这个代数关系式的认识和了解，是建立在动手操作和对数的分合上的。在后续学习中，学生还要通过对结果相等的加法算式的有序整理，归纳出算式形式与结果的变化规律，重新在加法运算意义上构建对原代数式的认知。如教学苏教版教材第一册第53页第6题（如图5）时，教师让学生在操作之后，依序呈现所有可能的情况（如图6），并且与得数是6的加法算式进行对应。

师：观察以上算式，大家有什么有趣的发现？

生1：它们的结果都是6。

生2：蜜蜂方阵被划分成两个三角形阵型，左边的三角形阵型从上到下不断增加，右边的三角形阵型从上到下不断减少。

生3：从上往下看这一列算式，被加数逐次加1，加数逐次减1，得数不变。

师：好眼力，你是从上往下看的。思考一下，得数不变，为什么前面加了1，后面刚好就减1呢？

生4：答案就在图中，总共有6只蜜蜂，分成两组，左边多了1只，右边自然就减少1只。

生5：如果从下往上看，左边每次减少1只蜜蜂，右边每次增加1只蜜蜂，总数不变。

师：其实不管沿着哪个方向看，它们的变化规律是恒定的。

生6：在一个加法算式里，一个加数增加1，另一个加数减少1，和不变。

师：想一想，以前见过这种现象吗？

生7：和圆圈涂色是一个道理，圆圈总数不变，涂色圆圈每增加1个，空白圆圈的个数就减少1。

生8：数的拆分与组合中也存在类似现象，总数不变，左端增加1，右端就减少1。