基于视觉的折射误差校正在位移测量中的研究
2021-03-24赵柳月王全保周平方段登平
赵柳月,王全保,周平方,段登平
(上海交通大学航空航天学院,上海 200240)
0 引言
位移测量技术在工程中具有重要意义,是其他变形测量的基础。为了解决高低温等非常温下进行亚像素位移测量的问题,研究了多种测量方法,包括非接触式全场变形测量技术,如云纹干涉法、数字图像相关方法、电子散斑干涉法、电子散斑干涉法等[1]。其中,数字图像相关(digital image correction,DIC)是一种非接触全场测量方法,量程大、精度高、设备简单、对测试环境要求低且易于操作,被广泛应用于位移场和应变场测量[2]。该方法利用图像处理技术对材料结构实现位移、变形以及应力测量,通过匹配变形前后散斑图像的对应点,确定散斑图像点的位移信息,从而确定全场位移。为了解决整数形式的像素坐标导致摄影测量精度只能达到像素级的问题,一般采用插值或亚像素算法求得更精确的亚像素位移,曲面拟合法是常用的方法之一[2]。
高低温环境下的数字图像相关方法需要利用保温装置将相机与外界非常温环境隔离。文献[2]表明相机装上保护装置后,透过光学窗口拍摄的照片足够清晰可进一步分析。文献[3]将玻璃折射简单类比为镜头径向畸变,通过畸变校正减弱了玻璃折射对光路改变的影响。Lyons等[4]用对比实验证明保温实验箱的光学窗口对图片质量和测量匹配有影响并最终影响数字图像相关方法的测量结果。然而当前对光学玻璃引起的折射误差进行详细地评估和修正的研究还不够充分。
本文推导了光学窗口玻璃折射下的误差模型,针对偏移误差提出了一种基于DIC方法的理论校正模型,以减小位移测量时由光学窗口折射引起的测量误差。通过研究光学窗口的玻璃折射光路,分析了其折射效应对偏移误差的影响,定量研究了玻璃和拍摄距离等因素对误差的影响,验证本文的校正方法对DIC测量精度的提高作用。
1 数字图像相关方法测量系统
1.1 测量系统
数字图像相关技术(DIC)是常用的变形测量技术和图像匹配技术。典型的二维数字图像相关方法测量系统如图1所示,系统由计算机、工业摄像机、照明光源和试件等构成。试件表面有承载物体信息的纹理图案,如果原有的纹理图案不足以表现其变形信息,则在其表面制作人工散斑[5]。

图1 数字图像相关方法测量系统
1.2 亚像素位移算法
摄像机对不同变形情况下的物体进行拍摄,数字图像相关算法通过相关函数寻找变形前后对应的像素点。为了得到精度更高的亚像素位移发展了多个亚像素位移算法,如牛顿-拉夫森(N-R算法),梯度法和曲面拟合法。文献[6]表明曲面拟合法能够兼顾精度和效率,常用于实际工况中。
像素点信息由以该像素点为中心的正方形子区表征。假设变形前后像素点坐标为(x,y)和(x′,y′),变形前后图像中对应的灰度值分别为f(x,y)和g(x′,y′),u和v表示横纵方向的位移,变形前后像素点对应关系为:x′ =x+u;y′=y+v。
相关函数是描述变形前后图像子区相似程度的函数,最小平方距离相关函数[6]表达式如下:
(1)
其中,2M+1是子区大小。在变形后的图像中搜索与变形前像素点(x,y)相似度最高的像素点,但通过相关搜索获得的位移u和v只能是整像素。为了获得更加精确的小数位移值,使用曲面拟合法进一步定位变形后像素点,常用二元二次多项式拟合相关函数曲面[6]。对于整像素变形像素点(x′,y′),邻域像素点如图2,拟合的曲面表达式为
(2)

图2 曲面拟合像素点
文献[6]证明拟合窗口大小为3×3时,精度最高、效果最好。因此有3×3个表达式,完全足够求解a0,…,a5的6个未知数。拟合的曲面求得极值时认为变形后的亚像素位置定位准确,即

(3)

(4)
综上,使用最小二乘法求解二次曲面的待求系数,拟合曲面的极值点坐标和亚像素位移分别为:
(5)
u=x′-x;v=y′-y
(6)
1.3 保温装置
非常温环境下,需要特殊的保护措施才能保证相机正常工作,图3展示了常见的I-CAN保护罐。保温罐可正常工作的温度范围为-200~100 ℃,内部温度保持在相机正常工作温度范围内,保温罐前端会开设一个由玻璃组成的光学窗口,相机在保温罐内透过光学窗口对图片进行拍摄。

图3 保温罐
2 玻璃折射误差及校正
2.1 折射误差
保温罐由一个保温罐体和一个光学窗口组成,相机通过光学窗口对待测物进行摄影,试样放置在观察窗口前方,保温罐内放置CCD照相机,其光轴垂直于样品表面。对于带有普通光学玻璃的保温罐,高低温下DIC实验中的测量光路如图4所示,由于玻璃折射的影响,像素点由真实的位置A点偏移至A′点。L为相机镜头到试件的距离,t为玻璃厚度,n为玻璃折射率,x为垂直方向像素点到中心的距离。Δx为因为折射产生的位移偏移。
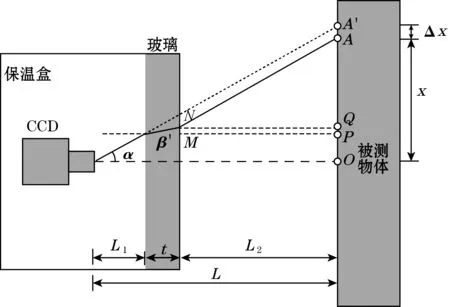
图4 包含玻璃影响的DIC实验的光路
分析图4中的偏移误差,由折射定律、几何相似关系及MN=OA′-AA′-AQ-OP,化简得到Δx的表达式为
(7)
式(7)是玻璃折射引起的像素点位移误差。为了进一步分析其对数字图像相关方法的位移精度的影响,必须对其进行简化处理。
为了分析像素点偏差规律,对两块玻璃a和b分别进行测试。玻璃各项参数如表1所示。图5展示了不同玻璃不同距离下不同阶次的拟合误差,计算范围为到中心点50 pixel距离内的点。

表1 玻璃参数
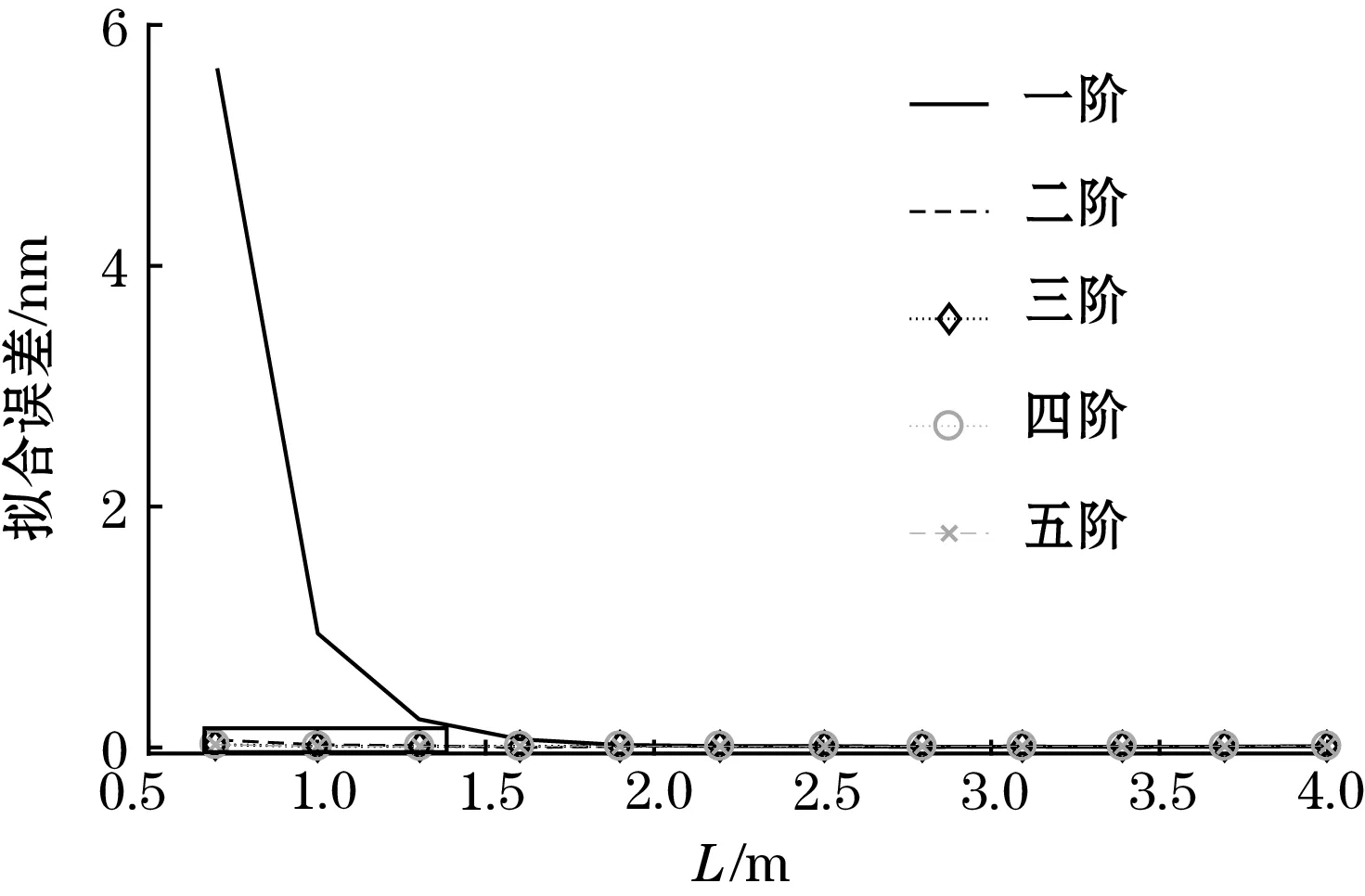
(a)玻璃a

(b)玻璃b图5 不同玻璃不同拍摄距离下折射偏移的拟合误差
图5表明当拍摄距离较小时,二阶和三阶等函数更好地拟合真实的偏移误差的走势,更高次项的拟合没有明显减小误差,但增加了计算量。根据误差拟合分析,可以合理假设偏移误差可以由x的多项式近似拟合,为了证明假设的正确性,令
(8)
式中f为一个关于x的未知函数,且满足x的阶数在-3~0之间。
这样的假设是基于二次和三次函数,可以很好拟合偏移误差的验证。由于x是小于1的数,为了简化,省略x高阶项x4,x6,x8得到:
(9)
最终可以得到:
(10)
任意方向上的偏移误差只与像素点到光心投影中心的距离有关,分解在x轴和y轴上为
(11)

至此,基于实验分析和假设验证合理推出折射误差模型,根据玻璃折射的各方向同理性折射仅对像素点相对于图像中心的模长有影响,该偏移误差随着像素点距离中心点距离的增大而增大,外部因素仅与玻璃折射率和厚度以及相机拍摄距离有关,偏移误差随着像素点的远离光心投影点的距离的增大而增大。
2.2 数字图像相关方法校正
玻璃折射使参考图像上的像素点A偏移了原来的位置,折射前后的坐标分别为(xA,yA)和(x′A,y′A)。经过变形之后A点在变形图像中的对应点表示为A′,其在折射前后的坐标分别表示为(xA,yA′)和(x′A,y′A)。则折射下的像素点的位移可以表示为:
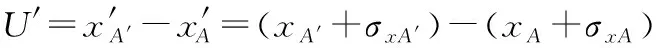
(12)

(13)
式中:σxA、σyA分别为变形前x和y方向的折射偏移量;σxA′、σyA′分别为变形后的x和y方向的折射偏移量,具体值由式(11)给出;U和V分别为变形前x和y方向的位移。
考虑到像素点坐标是整数的形式,直接进行坐标变换无疑在增加工作量的同时引入插值算法的误差。因此,寻求一个能够在经典曲面拟合的求解过程中便捷地处理玻璃折射误差的算法。在玻璃折射后的变形图像中使用相关函数寻找极值,通过整像素搜索得到整像素位移值。此时,待求参数为P=(a0,…,a6),确定n(n≥3)个匹配点代入式(3)和式(4)即可由最小二乘法求得待求参数的初值。
求得拟合曲面的系数后,根据式(5)和式(6)可以得到有折射的位移值,再根据式(12)和式(13)进行校正得到校正后真实的位移表达式,其中像素点到图像中心的距离近似为变形前的坐标距离,在推导时做了逆向的近似,因此互相抵消。真实位移值如下:
u={U′-K2[x′(x′2+y′2)-x′(x′2+y′2)]}/(1+K1)
(14)
v={V′-K2[y′(x′2+y′2)-y′(x′2+y′2)]}/(1+K1)
(15)
式中:U′和V′分别为变形后x和y方向的位移。
3 实验验证
3.1 标准标定板实验
为了对光学窗口的玻璃折射对数字图像相关方法测量精度的影响进行定性的分析,设计标定板实验在有玻璃遮挡和无玻璃的情况下对算法计算的位移结果进行研究,如图6。实验主要分为静态试验和平移试验。静态实验中可以对玻璃引起的偏移误差进行观察,对比理论结果,对玻璃折射的理论误差模型的推导结果进行验证。平移试验是为了研究光学窗口的玻璃折射对位移测量的影响以及校正方法的有效性。

图6 实验图片
3.2 折射误差模型验证
标定板实验共分为3组,在相机和试件静止的情况下,对镜头前加玻璃进行保温装置光学窗口的模拟,镜头情况分别为无玻璃-有玻璃遮挡,无玻璃-左半部分玻璃遮挡,无玻璃-右半部分玻璃遮挡。使用2个玻璃分别做了对比实验,实验结果类似。下面给出玻璃a的实验结果。
其中实验步骤中无玻璃的图片可以相互验证,位移值近似为0可认为平台稳定。图7~图9展示了在摄像距离为1.5 m的情况下,在玻璃分别对镜头进行全遮挡、左半部分遮挡、右半部分遮挡下,与未进行玻璃遮挡拍摄的图片进行数字图像相关方法计算得到的u方向的位移变化三维图。可以看出玻璃折射对位移有着明显的影响,有玻璃遮挡的部分位移明显呈现以图片中心为辐射点,越向外位移量越大的趋势,与折射误差模型相符合。图中展示的测量范围是100~400 pixel,由玻璃折射产生的偏移误差达到了4个像素,测量范围变大误差将更大。像素点的位移是计算应变、匹配的基础。相应地,折射也会引起其他力学信息的测量。

图7 全部玻璃遮挡下折射导致的u方向位移三维图

图8 左半玻璃遮挡下折射导致的u方向位移三维图
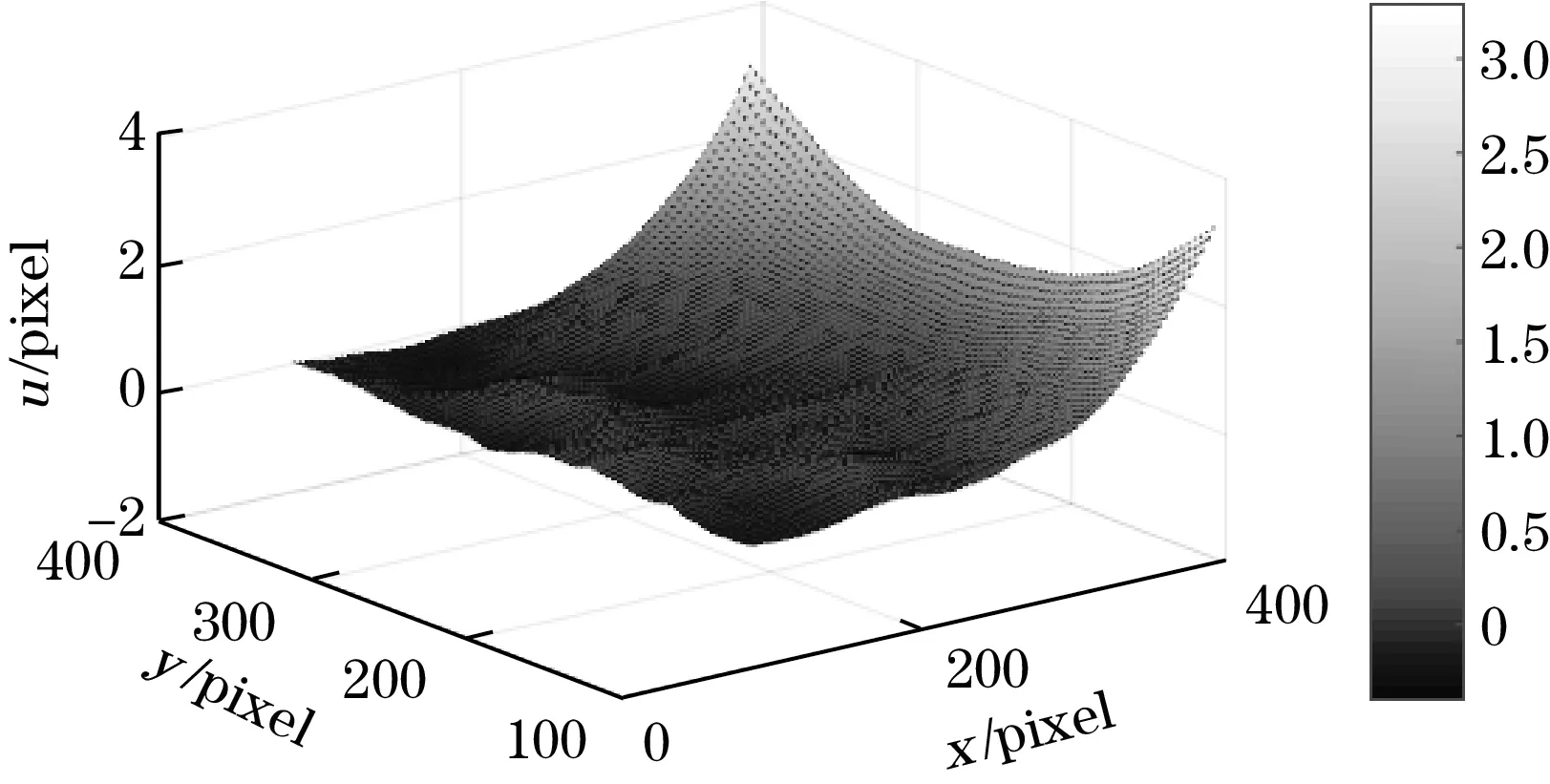
图9 右半玻璃遮挡下折射导致的u方向位移三维图
3.3 校正方法验证
采用本文提供的校正方法,根据玻璃参数和拍摄距离常量参数对变形前后的图片进行误差修正,最终得到校正后的图片的u方向和v方向的三维位移图,如图10所示。对比校正前后的图片可以看到,位移偏差基本上由4 pixel降到了0.2 pixel。允许测量中微小变动的误差存在,基本上可以认为通过本文的校正方法,玻璃折射对位移产生的偏移误差被显著减小,能够很好地提高数字图像相关方法的测量精度。

图10 校正后的位移云图
进一步研究平移情况下玻璃折射的偏移误差对测量精度的影响。在玻璃遮挡的情况下,对标定板进行拍摄,标定板在仪器控制下每次进行1 mm的水平移动,根据拍摄情况1 mm对应2.5 pixel。不同位移下,无玻璃拍摄图片与镜头覆盖玻璃的拍摄图片分别作为变形前后图片,使用数字图像相关方法对其进行计算,得到校正前后的位移量如表2所示,未校正的最大绝对误差为0.192 9 pixel,校正后的最大绝对误差为0.030 9 pixel,随着测量范围的增大,校正对测量精度的改善会更加明显。

表2 位移计算结果比较 pixel
图11为位移测量值误差。从图11可以看出不进行校正的图片由于偏移误差的存在,导致数字图像相关方法最终得到的位移测量值不稳定,误差较大。经过校正后的位移测量误差低于3%,提高了5%左右。整体测量误差小于未校正的测量误差,且测量结果更加稳定。
4 结束语
针对非常温环境下,摄影测量技术需在保护装置中进行,无法避免光学窗口的玻璃折射影响的问题,本文提出可靠的误差模型及校正方法。本文通过分析保温装置光学窗口的玻璃折射光路,在合理的简化、假设基础上提出了玻璃折射误差模型,并根据误差模型对数字图像相关方法进行校正。该误差模型可以准确地表征折射带来的位移偏差,相应的校正方法可以有效地降低数字图像相关方法测量中玻璃折射的影响,提高匹配的精度和位移测量精度,解决了玻璃厚度和测量精度的制约问题,可以在低成本光学玻璃的情况下进行高精度的测量。

图11 位移测量值误差
