振弦式陀螺频率检测结构设计与振动分析

陈志龙，刘 鹏，黄 鸣，舒 凯

(1.南昌理工学院，江西南昌 330044;2.华东交通大学机电与车辆工程学院，江西南昌 330013)

0 引言

陀螺是构成惯性导航系统的核心部件，为了测出从地面飞向太空的火箭、人造卫星和宇宙飞船等宇航设备的角速度和转动角度，并控制他们的姿态，陀螺是必不可少的[1]。振动式陀螺是应用微机械加工技术与微电子工艺技术制作的一种惯性传感器，它具有体积小、质量轻、功耗低、易于集成等特点，在车辆驱动防滑控制系统、机器人姿态感知与控制系统、平台稳定系统、炮弹制导等领域得到了广泛的应用[2-4];振弦式陀螺是把振动式陀螺的工作机理与振弦式传感器的测量机理相结合的一种陀螺。

驱动系统与检测系统是振动式陀螺重要组成部分，驱动系统的主要功能是使敏感部件产生高频振动，振动式陀螺的驱动方式主要是运用场力来驱动，如静电力、电磁力等。文献[5-7]报道的振动陀螺都是采用静电驱动，虽然静电驱动具有功耗低的特点，但工作电压高，与目前片上常用的工作电压(<5 V)不兼容，难以适应系统集成与微电子器件的发展趋势[8]。检测系统的主要功能是对敏感部件受到外界信号的检测，振动式陀螺的检测方式主要有运用压电、光电、频率来检测信号，文献[9]报道的压电振动陀螺，该陀螺输出非线性特性优于0.1%FS，但制造工艺比较复杂；文献[10]提到了一种光电检测传感器，该传感器能达到分辨率为0.1%FS，数据拟合曲线比较线性，但还处在试验阶段，传感器体积较大。随着高深宽比微结构加工的半导体工艺、设备的发展，原先困扰电磁驱动与频率检测研究的加工手段问题已不再突出[11]；频率检测能获得较高的频率分辨率。

1 振弦式陀螺的工作原理与频率检测模型

1.1 振弦式陀螺工作原理

图1为振弦式陀螺的简化模型。质量块m固连在旋转坐标系的xy平面内，模型具有2个振动模式，每个模型简化为弹簧-阻尼-质量模型。假定质量块在y方向受到某种激励作用而受迫振动，而z轴有角速度Ω输入时，质量块在x方向就会受到交变的科氏力(Coriolis force)作用而沿x轴方向产生诱发振动，从而可通过振弦的频率检测，测出角速度输入量[12]。

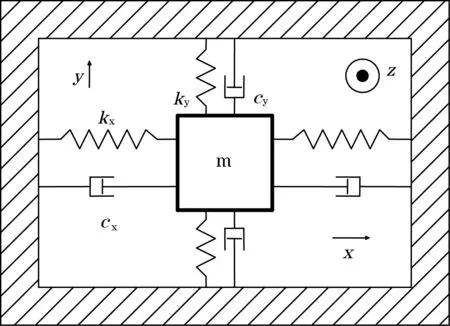
图1 振弦式陀螺的简化模型

1.2 振弦式陀螺频率检测数学模型

振弦式陀螺敏感元件为振弦丝结构，其具有较大的长径比，振弦式陀螺在工作时，检测结构模型可以简化为两端固支的振弦丝结构，振弦在振动时受力如图2所示。

图2 两端固支弹性弦丝振动受力示意图

取振弦上任意一微小段(x，x+dx)，振弦传感在工作时，其振动幅度相对比较小，所选微小段对应弧长近似为dx，对微段进行受力分析有如下平衡式：

式中：β为阻尼系数；ρ为振弦丝的线密度。

由于振弦振动的幅度相对比较小，α1≈α2≈0，则有：

(2)

振弦式陀螺采用永磁体电磁间歇式驱动,初始时刻所有的点均处于平衡位置,则有初始条件：

y(x，0) =0，y(0，t) =0，y(1，t) =0

对于永磁体电磁驱动的振弦式陀螺信号敏感系统来讲，高频信号的检测难度要高于低频信号，因而要尽量保证振弦式陀螺振弦敏感结构处于基频状态。当振弦处于1阶振动模态时，振弦中心处振幅最大，在该处对振弦振动信号进行检测，有利于提高信号的信噪比，因而只需解算出振弦中心1阶振型的振动方程[13]。

(3)

约去高阶小量整理并由欧拉公式得到振弦中点的振动方程为

(4)

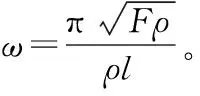
则振弦丝振动的频率可用式(5)表示:

(5)

通过检测振弦自由振动的基频，利用上述公式即可解算出振弦所受科氏力大小，进而可计算出输入角速度大小。

2 振弦式陀螺检测结构设计分析

振弦式陀螺电磁驱动初步结构模型如图3所示。它是由一对背轭架为支撑的对杆磁铁和一个带有支架的线圈框架组成的，线圈框架位于永磁体边界内，获得均匀的磁感应强度。

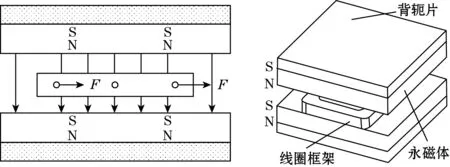
图3 驱动结构设计示意图

2.1 振弦式陀螺频率检测部分结构设计

振弦式陀螺采用振弦与中心敏感质量块组合的方式来敏感科氏力，通过检测振弦上的频率改变量来实现输入角速度ω的转化。由驱动结构设计初步得到的参数可知，线圈框架的尺寸参数：宽度为15 mm、长度为30 mm、厚度为3 mm；314不锈钢丝韧性好、抗磨损、硬度高、弹性强，选择314不锈钢丝作为振弦材料。采用软铜板簧片作为驱动框架的两端支撑，这样有利于线圈框架的驱动且可以克服线圈框架的重力。

2.2 振弦线径对模态频率的影响

振弦的线径不同会影响振弦的振动，也会影响驱动系统与检测系统对振弦驱动与检测。根据314不锈钢的材料特性，定义振弦模型的弹性模量为2.06×1011N/m2，泊松比为0.3，密度为7 750 kg/m3，材料阻尼为0.02。根据振弦式陀螺的初步结构尺寸，选择30 、50 、80、100 μm的线径、长度为30 mm的不锈钢丝，建立有限元振弦模型，应用ANSYS软件进行分析，分析数据处理采用基数为1.5×104Hz上的增量值，分析结果如图4所示。

由图4分析结果可知，随着振弦线径的增大，各阶响应频率也随之增大，这是由于振弦线径的增大，振弦刚度系数也随之增大，使得振弦基频以及高阶频率也随之增大。但在选择振弦时也需考虑振弦在振动过程中受重力、空气阻力影响，如果振弦线径太大，则振弦振动产生的驻波波节相对较短，使得振弦弦振动时间较短，电磁驱动周期增大，且振幅也会减小，不易驱动；目前国内外的振弦传感器选用的振弦直径均在50 μm左右；其次由振弦式陀螺频率检测数学模型可知，振弦振动频率与振弦长度成反比，对于受相同科氏力的振弦而言，长度越长，振弦振动频率越小，传感器灵敏度下降，且会带来振弦式陀螺结构尺寸的变大；基于振弦式陀螺结构尺寸以及市场上能满足的要求，选择线径为30 μm，长度为30 mm，振弦式陀螺频率检测初步结构模型如图5所示。

图5 频率检测结构设计示意图

3 振弦式陀螺结构分析与优化

对振弦式陀螺谐振频率分析时可以利用瑞利能量法得到振弦式陀螺机械结构各阶振动模态的谐振频率的表达式[14]：

(6)

式中：kτ为板簧片连接方向τ的刚度系数；mτ为线圈驱动框架等效质量。

振弦式陀螺机械结构各阶振动模态与kτ和mτ有关，而kτ、mτ也仅与结构材料和尺寸有关，因此可知，振弦式陀螺各阶模态的谐振频率主要取决于振弦式陀螺板簧片在各方向的刚度系数和被板簧片所带动部分的等效质量，这两项参数都由振弦式陀螺的结构材料和尺寸决定。因此，当材料一定时，可以通过改变振弦式陀螺的结构尺寸达到模态匹配的效果。

3.1 板簧片结构参数对驱动模态的影响

采用单一变量分析原则，应用ANSYS有限元软件分析板簧片结构参数对振弦式陀螺驱动模态谐振频率的影响；在对板簧片长度仿真分析时，仿真条件为：驱动框架采用树脂材料，板簧片采用铜铝合金材料，线圈驱动框架采用等效质量，激振力为1 N，两板簧片连接端面全约束进行仿真。

3.1.1 板簧片长度的影响

选择板簧片宽度为3 mm，厚度为0.1 mm，考虑振弦式陀螺的设计尺寸，取板簧片长度为3～9 mm，步长为1 mm。图6为板簧片长度与模态频率的关系。振弦式陀螺的各阶模态频率随着板簧片的长度增长而不断减小。在板簧片长度增大至8 mm时，前三阶模态频率趋于稳定，基于振弦式陀螺抗振考虑，1阶模态频率须在1 kHz左右，3阶模态频率须在2 kHz以上，但也不能过高，不然会使高频驱动电路设计相对复杂；综合考虑振弦式陀螺尺寸，选择板簧片有效长度4 mm为宜；这样有利于减小振弦式陀螺整体结构尺寸。

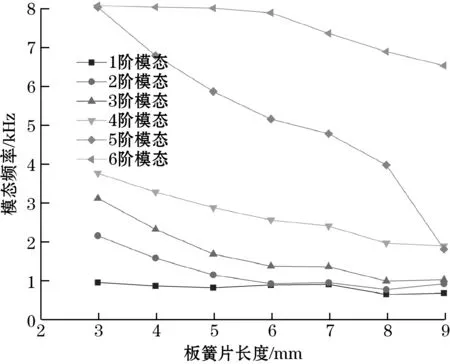
图6 板簧片长度对驱动模态频率的影响

3.1.2 板簧片厚度的影响

选择板簧片宽度为3 mm，有效长度为4 mm，考虑振弦式陀螺的设计尺寸与电磁驱动最大驱动力，取板簧片厚度为0.1～0.5 mm，步长为0.1 mm进行仿真。图7为板簧片厚度与模态频率的关系。随着板簧片厚度增加，驱动模态频率也逐渐增加，这是由于板簧片厚度的增加使得板簧片刚度系数增加，前四阶模态频率增加较快。考虑不让驱动力过大和振弦式陀螺抗振等问题，选择1阶模态频率大于1 kHz，4阶模态频率低于5 kHz，选择板簧片厚度应在0.2～0.3 mm。

图7 板簧片厚度对驱动模态频率的影响

3.1.3 板簧片宽度的影响

选择板簧片有效长度为4 mm，厚度为0.2 mm，考虑振弦式陀螺的设计尺寸与板簧片纵向抵抗重力刚度，取板簧片宽度为2～3 mm，步长为0.2 mm进行仿真。如图8所示，从板簧片宽度与模态频率的关系可知，随着宽度的增加，各阶模态频率有微幅度增加，在宽度为2.8 mm左右，2、3、4阶模态频率有降低趋势；考虑振弦式陀螺抗振性以及抵抗线圈框架重力因素的刚度问题，选择板簧片宽度应在3 mm为宜；这样有利于在电磁驱动时受力，且纵向刚度可以很好地抵抗线圈框架的重力，很好地抵抗外界频率的干扰。

图8 板簧片宽度对驱动模态频率的影响

3.2 敏感质量块结构参数对检测模态的影响

振弦式陀螺敏感科氏力最重要的一部分就是敏感质量块结构，合理设计敏感质量块结构参数对于提高结构灵敏度以及提高振弦式陀螺振动频率具有重要意义。图9为振弦式陀螺敏感质量块与限位器示意图。

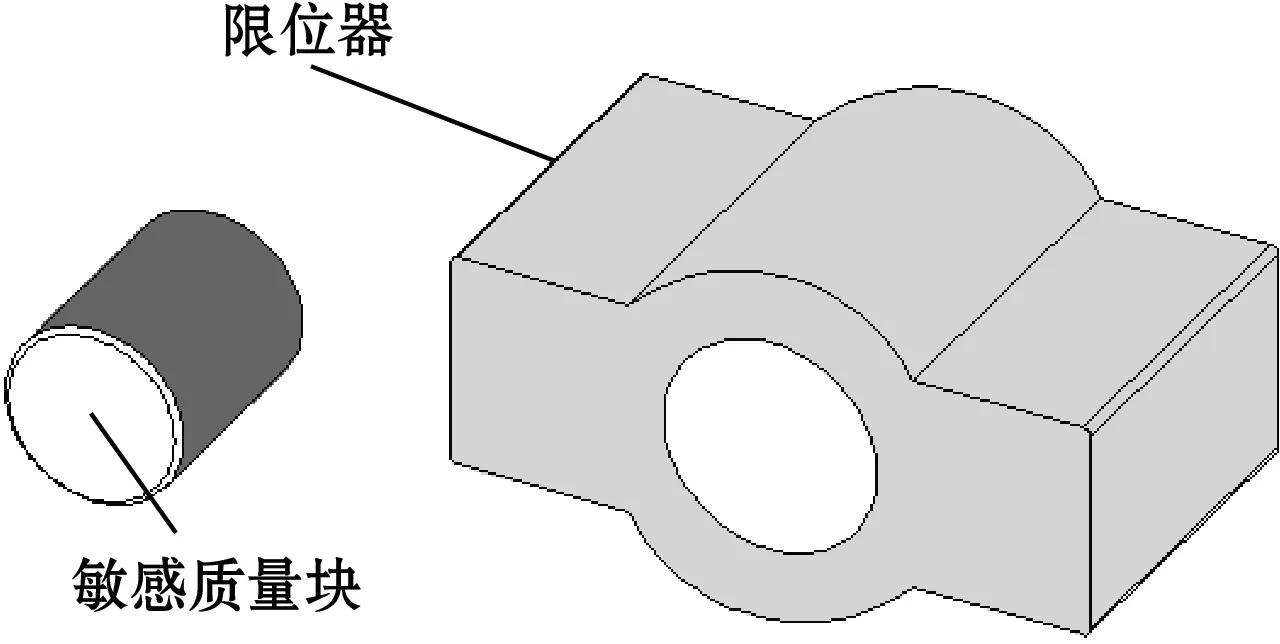
图9 敏感质量块与限位器示意图

3.2.1 敏感质量块直径对检测模态的影响

考虑质量块结构以及加工装配问题，限位器采用树脂材料，质量块采用圆柱紫铜材料。选择长度为4 mm，考虑敏感质量块的设计尺寸，取质量块直径为0.6～3 mm，步长为1 mm，进行仿真分析。如图10所示，振弦式陀螺的各阶模态频率随着敏感质量块直径增大而不断减小，当质量块直径增加到2 mm以上时，振弦式陀螺检测1阶模态非常低，非常容易受外界的干扰，考虑1阶模态频率大于1 kHz、检测模态与驱动模态相匹配、敏感质量块重力对振弦频率的影响问题，选择敏感质量块直径为1 mm左右为宜。

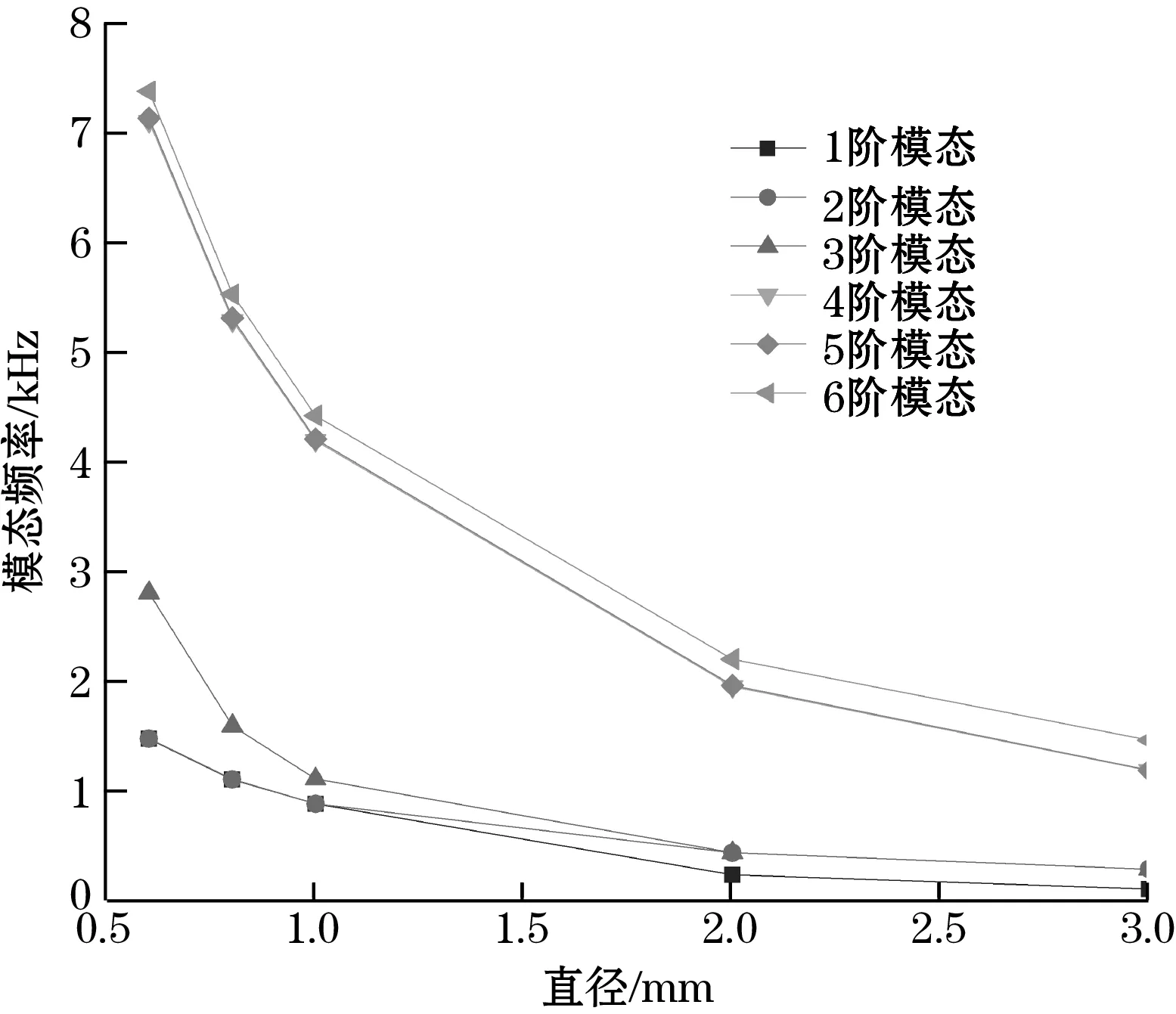
图10 敏感质量块直径对模态频率的影响

3.2.2 敏感质量块长度对检测模态的影响

在进行敏感质量块长度仿真分析时，选择振弦长度为30 mm，质量块直径为0.8 mm，取长度为2～6 mm，步长为1 mm；如图11所示，振弦式陀螺的1、2阶模态频率线几乎重合，且振弦式陀螺的各阶模态频率随着敏感质量块长度增大而不断减小，前三阶模态减小的幅度较小；长度增大到3 mm时，高阶模态下降的幅度较大。质量块长度增加到6 mm时，振弦式陀螺检测1阶模态非常低，非常容易受外界的干扰，考虑1阶模态频率大于1 kHz、检测模态与驱动模态相匹配、敏感质量块重力对振弦频率的影响问题，选择敏感质量块长度为4 mm。

图11 敏感质量块长度对模态频率的影响

4 振弦式陀螺振动响应仿真分析

4.1 振弦振动有限元静态分析

在ANSYS Workbench软件中选择不锈钢材料，定义振弦模型材料属性，314不锈钢材料属性如表1所示。

表1 314不锈钢材料属性

根据前面章节确定的振弦尺寸：选择线径为30 μm，长度为30 mm。用Solidworks三维软件建立振弦模型，并保存IGS格式文件，导入到ANSYS Workbench 软件Static Structural模块中；首先定义材料参数，采用四面体单元划分网格，设置单元长度为0.1 mm，采用全约束振弦的一端，另一端采用Y、Z方向约束，在X方向施加1 N的预应力，最后进行静态求解。振弦预应力加载整体节点变形量图如图12所示。

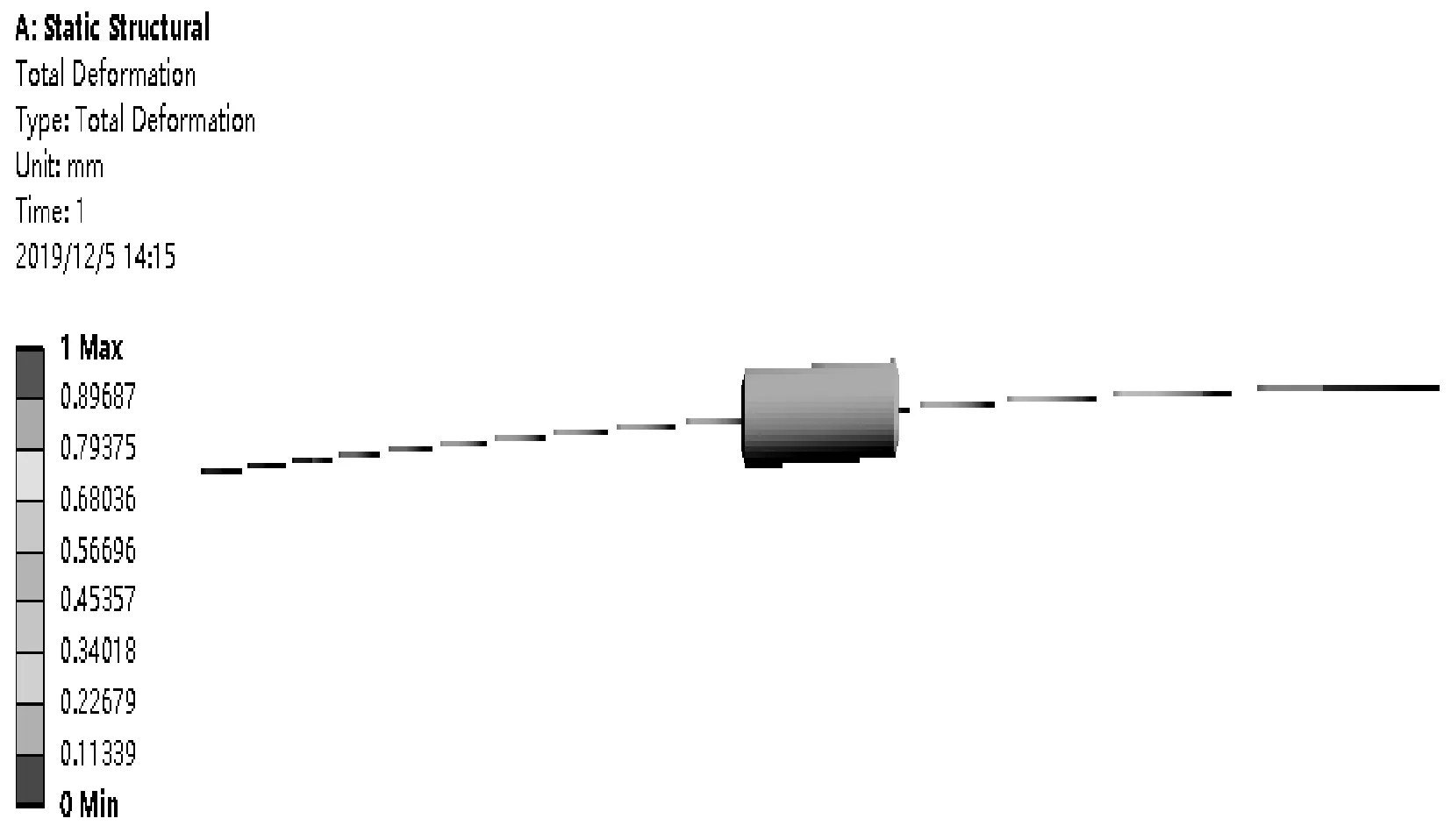
图12 振弦预应力加载整体节点变形量图

在振弦绷紧的状态下，振弦在X、Y、Z方向上的最大变形量与最小变形量如表2所示。

表2 振弦在不同方向上的变形量 mm

从有限元静态分析与有限元分析可以看出频率检测振弦部分振动时会产生小变形状态，但是变形量相对较小，对驱动没有带来影响。

4.2 振弦振动有限元模态分析

模态分析技术常用于结构固有振动特性的研究，因此为了研究频率检测结构的固有振动特性，利用ANSYS Workbench有限元分析软件中的模态分析Pre-Modal模块对频率检测结构进行有限元模态分析。将上一步完成的预应力静态分析结果加载到模态分析过程中，加载模态为前六阶，然后开启模态求解器分析有预应力作用下频率检测振弦的6阶模态值，图13为频率检测振弦的1、2模态。

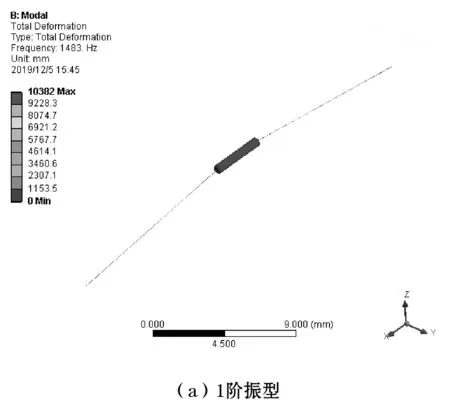
图13 频率检测振弦的1、2阶模态

在做Pre-Modal有限元模态分析的同时也可以得出每阶模态所对应的频率大小，结果如表3所示。

表3 振弦6阶模态频率值 Hz

4.3 振弦陀螺整体结构有限元仿真分析

结合振弦式陀螺初步设计与结构尺寸分析结果，优化设计振弦式陀螺结构，设定振弦式陀螺振动板簧片结构参数：4 mm ×0.2 mm ×2.8 mm，敏感质量块结构参数：直径为0.8 mm、长度为4 mm，线圈框架的尺寸参数：宽度为15 mm、长度为30 mm、厚度为3 mm；为了验证设计的振弦式陀螺结构的可行性，通过SolidWorks三维软件建立陀螺模型，采用ANSYS有限元仿真方法对振弦式陀螺的振动响应进行分析，图14为仿真网格划分与1阶模态图。

图14 振弦式陀螺仿真图

在进行优化后的振弦式陀螺驱动结构振动响应分析时，施加驱动力为1～10 N,步长为1 N；如图15所示，振弦式陀螺驱动结构振动响应随着驱动力的增大而增大，且驱动力与位移量之间具有很好的线性关系；从模态分析中得到驱动频率达到1 922.6 Hz；从而可以很好地减小电磁驱动难度，提高陀螺框架控制精度，且驱动过程中驱动基频很好地抵抗外界干扰，具有很好的驱动响应。

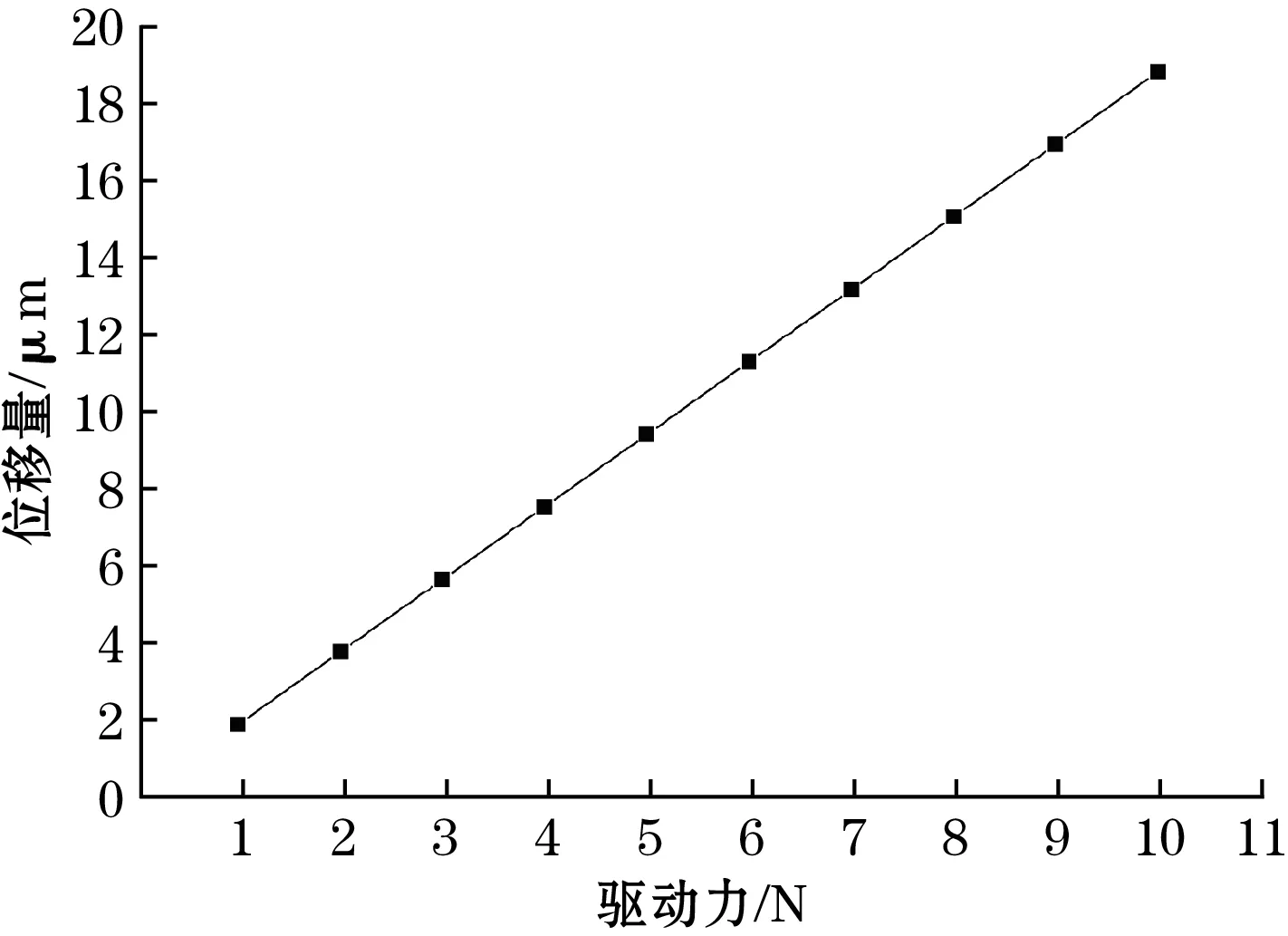
图15 驱动力大小对驱动结构位移量的影响

5 结束语

采用电磁驱动与频率检测的工作原理建立了振弦式陀螺频率检测数学模型；应用ANSYS软件分析了振弦线径与响应频率的关系，振弦线径增大时，各阶响应频率也随之增大，使得振弦基频以及高阶频率也随之增大；从初步的振弦式陀螺检测结构设计中，得出振弦式陀螺频率检测系统主要受板簧片尺寸、振弦尺寸、敏感质量块尺寸等因素的影响。通过分析频率检测系统中板簧片结构尺寸对驱动模态的影响，优化了振弦式陀螺整体结构，建立了振动响应仿真；结果表明频率检测模型频率满足驱动与检测设计要求。