D-S证据理论在教师授课认真程度综合评价中的应用*

◆布少聪 杨波

0 引言

高校教师教学评价是非常重要的一个教学环节，常用的评价方式是学生评价和督导组听课评价二者结合。学生评价即学生在网上匿名一次性评价，打分受较大主观因素影响，如课程难、教师要求高、不及格率高的课程，学生给的分数往往偏低。督导组听课一般1～2次，难以对一学期的教学作出全面评价，且非背靠背评分，评分难免主观。两种方式的评价意见均不够具体，且两项成绩合成缺乏科学依据。

鉴于此，可以将教师授课认真程度综合评价和研究生学科核心课程检测技术与自动化中的基于D-S证据理论的信息融合方法结合起来，作为课程的研究型设计报告，以全面评价教师的投入程度。以某教师授课情况作为研究对象，通过建立两层评价指标体系，由听课教师或学生进行百分制的单项指标评价，然后按不同的权重给定融合判定依据，采用D-S证据理论对教师授课质量进行综合评价，提供多角度的分析信息，使评价结果更具客观性、科学性和有效性。

1 问题描述

基于D-S证据理论实现对教师授课认真程度的评价，首先要构建评价指标体系、评定标准与规则和处理原始数据。

1.1 评价指标与辨识框架

通过调研，将教师授课认真程度的评价指标设为八项，可理解为D-S理论中的“证据”；将这些指标分为两类，构建两级指标评价体系，即完成两次D-S证据理论信息融合。定义辨识框架Ω中包含A到E五个元素，表示从高到低的程度，用于评价各项指标以及指标最终合成的“认真程度”。具体的指标及评价等级描述如表1所示。表中的指标说明如下。

表1 教师授课认真程度评价项目

1）一级指标“客观状况”下设五个二级指标。

①出勤情况：参照学校关于教学事故的说明拟定。

②课堂不良行为发生率：参照学校关于教学事故的说明及教师规范拟定。

③知识信息量：教师在一堂课上讲授有关课程主题的内容多少，选择用时间比例来衡量（与课程内容相关的时间/一节课的总时间）教师在该节课中的真实工作量。

④授课形式：主要是描述教学手段是否多样化。

⑤脑力负荷水平：脑力负荷（mental workload）可理解为人在单位时间内的脑活动量、大脑资源占有率和信息处理能力等[1]，研究表明，该水平与工作投入度和工作能力挂钩[2-3]，选用该指标衡量教师一节课的工作投入与工作效能。

2）一级指标“学生评价”下设三个二级指标，每个学生仅以自身的感受作出评判。

1.2 情景假设与数据来源

本设计中假定每位教师一学期授64节课，并有100位学生参与评教。对于“客观状况”下属的指标，每节课进行一次评价，如此统计并分类得到64个评价结果。对于“学生评价”下属的指标用同样的方式统计并分类得到100个评价结果。

对于“脑力负荷水平”这项指标，可采用生理测量法完成，或通过主观评价法[使用美国航空航天局提供的脑力负荷评价（NASA-TLX）量表和工作能力指数（WAI）量表]、主任务测量法、辅助任务测量法测评[2]。

2 综合评价设计方法及实例分析

如上文所述，各指标的评价结果统一到Ω=｛A,B,C,D,E｝中，数据合成过程使用到的方法如图1所示。首先对原数据概率化，得到八项指标m1～m8的基本概率分配矩阵，它以各指标为行，以各等级评价为列；通过度量证据相似性获得每个指标的可信度，作为证据融合时的权重；再利用可信度权重对两大类指标分别进行第一次D-S证据理论融合，得出两个一级指标的基本概率分配M1和M2；之后利用信息熵获取一级指标权重，进行第二次数据融合；根据判定准则分析最终概率分配，从而得出关于认真程度的判定。

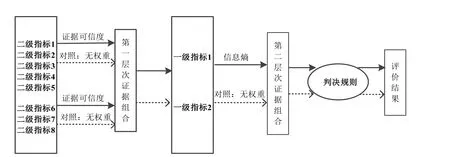
图1 基于D-S证据理论的教师授课认真程度评价方法流程框图

2.1 原始数据概率化

每个指标每个等级对应的概率数即为该位置原始数字与测试总量之比。对于前五项，每个指标的测试总量为64（课时数），后三项每个指标的测试总量为100（参评学生数）。为方便后续计算与融合，遇到概率数为0时，将其改为0.000 001，同时将该指标中最大概率减去0.000 001，以保证对后续影响最小。得到一个不含0值的8×5的概率分配矩阵Origin_matrix。

2.2 利用证据相似度获取第一层次D-S证据合成时的权重

此处获取权重并引入证据融合是为了缓解证据之间的冲突，权重采用度量证据相似性方法获得[4]。利用证据间的关联度，由证据可信度来确定证据权重，即若某个证据与其他证据的冲突较小，则可信度较高，权重较大。下面结合程序设计给出计算方法。

定义一个度量证据体间相似程度的证据距离函数来表示两个指标间的相似性：

该式计算的是欧式距离，值越小说明两个证据之间越相似，冲突越小。

把每两证据之间的距离值正则化，然后聚集起来构成证据相似性距离矩阵：

利用信度函数confi=f(si)=(1-si)e-si计算每一个证据的可信度。可信度confi描述该证据的重要程度和融合结果的影响程度。用于计算可信度的信度函数应选用单调递减型，且值域配合定义域为（0,1），董增寿等[4]选择上述指数关系函数。将同一证据集中的n个confi值聚合为矩阵，得到两大类指标对应的可信度矩阵Conf11（1×5）和Conf12（1×3）。

按式（2）归一化可信度形成证据权重：

由此得到两大类指标对应的权值矩阵Weight11（1×5）和 Weight12（1×3）。

2.3 利用信息熵获取第二层级D-S证据合成时的权重

第一层次D-S证据理论融合后，得到两个一级指标的基本概率分配M1和M2，由于融合证据数目较少，因此忽略冲突情况，而是基于人工智能领域中决策树的相关知识，考虑用信息熵（Entropy）的概念来计算权重，每个证据的信息熵为：

熵描述了信息的纯度，值越小表明系统越有序，信息确定性越大，其值介于“0到Ω中元素数”之间，因此根据这种关系计算权值：

每一层次得到权值后，按式（5）计算即可得到加权平均证据，之后可按照规则合成证据。

2.4 D-S证据理论合成规则

在这里仍然要列出D-S证据理论合成公式：

其中归一化常数因子K为：

本设计两次D-S证据理论合成均用到式（6）和式（7），并且在对照实验中更是直接利用两式对证据进行融合，因没有计算权重，在后文中称此为传统方法。所有证据融合完成后得到最终的基本概率分配BPA，决策的基本原则是选择BPA中拥有最大概率数的等级作为终期评价结果，即为A～E中的一个值，在此前提下细化规则如下。

1）若最大概率数与第二大概率数之差≥0.1，则认为拥有最大概率数的等级占绝对优势，将该等级作为终期评价结果。

2）若最大概率数与第二大概率数之差＜0.1，则认为两者有比重相当；若最大概率数所属等级优于第二大概率数所属等级，则终期评价结果为“最大概率数所属等级-”，反之则终期评价结果为“最大概率数所属等级+”。

综上，可能的评价结果有{A,A-,B+,B,B-,C+,C,C-,D+,D,D-,E+,E}共13种。

2.5 实例分析

以李老师为例，原始数据信息如表2所示，经概率化并作非零值处理后的概率分配如表3所示。从直观的角度看，李老师的授课认真程度中等。

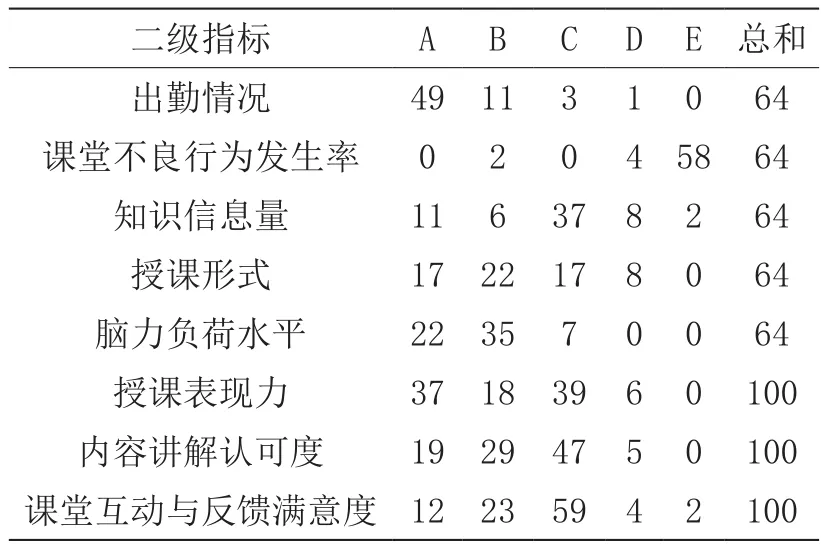
表2 李老师各项指标原始评价统计信息

表3 李老师评价指标的基本概率分配

可以看到m2与m1～m4存在相对最为严重的冲突，因此可以尝试通过上文介绍的方法，获得可信度权重来减弱m2对于合成结果的影响。计算得出各类矩阵：

各证据的可信度分别如下：

conf11和conf12值直接反映该证据对于其他证据的支持程度。conf11中的第一和第三个元素大小相当，也就是m1与m3的支持度相当，m4和m5是同样的道理，但m2可信度明显比其他四个指标低，这符合原始数据中的冲突情况。而conf12中三指标的可信度大小相差不大，结合其原始数据信息看，三证据的概率分布确实有相同的情形（C级概率均为最大，DE的概率数都接近0）。通过实验验证上文获得的可信度权重是合理的。

第一层次数据融合时的各证据权重分别如下：

Weight11=[0.186 3 0.075 2 0.206 4 0.287 9 0.244 3]

Weight12=[0.312 3 0.357 0 0.330 7]

两类别内部各证据的加权平均基本概率分配为：

Mean_BPA11=[0.338 5 0.286 3 0.231 2 0.069 4 0.076 4]

Mean_BPA12=[0.223 1 0.235 8 0.484 7 0.049 8 0.006 6]

第二层次数据融合时的两个一级指标权重如下：

weight2=[0.474 5 0.525 5]

加入权重的方法与传统方法在融合结果和评价结果中的差异如表4所示。

用传统方法得到的认真程度为B，加入权重后为C。如上所述，李老师的授课认真程度中等，因此，加入权重的方法更适合评估教师授课认真程度。从理论层面分析，是因为在第一层次证据融合中，m1～m5中的m2与其他证据冲突较大，若不加以缓解，就会出现传统方法实验结果BPA11_trad中极端的概率分配情况；设计中加入证据可信度权重后，BPA11的概率分配不仅值不再是极端接近于0或1，其总体分配也更符合原始数据带来的直观信息。

3 结束语

针对目前高校教师授课评价中存在的问题，本文利用研究生课程检测技术与自动化中多元信息融合方法的授课内容，以课程研究型设计报告的形式对教师授课认真程度综合评价进行研究。建立双层评价体系指标，从主观和客观两方面制定多角度评价指标，分别利用证据相似度和信息熵获取第一层次和第二层次D-S证据合成时的权重，采用D-S证据理论对教师授课质量进行综合评价，对综合评价的有效性进行验证，评价结果更具客观性、科学性和有效性。

表4 两种方法的两次证据融合结果与评价结果对比