聚硅氧烷硅胶的黏超弹性力学行为研究

黄锐宇 于培师,1) 刘禹 田常录 常晋源 王鹏飞 赵军华,2)

∗(江南大学机械工程学院江苏省食品先进制造装备技术重点实验室,江苏无锡 214122)

†(中国科学与技术大学工程科学学院,合肥 230027)

引言

多孔材料因其独特的微结构而具有优异的减振、轻质、隔热、隔音等性能,如泡沫塑料、泡沫金属等在航空航天、石油化工、交通运输等领域得到了广泛的应用.传统发泡技术通过物理或化学方法在材料内部产生大量空隙,可实现多孔材料的发泡法制备.此类方法对整体孔隙率可实现较为精确的控制,但孔的尺寸与空间分布依然具有较大随机性[1],导致传统发泡材料的结构均匀性较差、且易导致局部提前老化.随着航空航天等特殊高精密高强度领域的发展,对多孔材料的结构,寿命等性能的要求不断提高,而传统发泡工艺无法克服气泡的随机性分布而面临巨大挑战.直书写3D 打印技术的发展[2]为制备多孔材料提供了另一种途径,该技术可对孔的尺寸与排列方式进行精准控制[3-4],能够有效地避免传统制备方法带来的结构不均等问题[5-6].聚硅氧烷硅胶以其较低的成本、弹性优良、断裂伸长率大、耐化学腐蚀、抗腐蚀老化、惰性好及优异的流变性能而备受关注[7-8],逐渐成为直书写3D 打印的优选材料.然而,为了实现多孔结构的精准设计与拓扑优化,需要对材料本身的力学行为进行充分的测试与表征,并建立精准的材料本构模型,从而更加有效地优化不同设计方案的性能参数,为结构优化奠定基础.

针对聚硅氧烷硅胶具有复杂的静、动态超弹性特征,本文首先通过解耦其超弹性和黏弹性本构关系来确定其黏超弹性本构方程的基本框架[9-10],其次通过不同类型的试验确定了上述黏超弹性本构模型的各项参数.基于该本构模型,对落锤冲击下的该硅胶薄片进行了有限元模拟,并结合落锤冲击试验与有限元结果进行对比,验证了本文确立的该硅胶黏超弹性本构模型的有效性.

1 黏超弹性本构模型

1.1 超弹性模型

聚硅氧烷硅胶是各向同性的体积近似不可压缩材料,在均匀应变下,其高弹性特征可由超弹性本构模型描述[11-14]

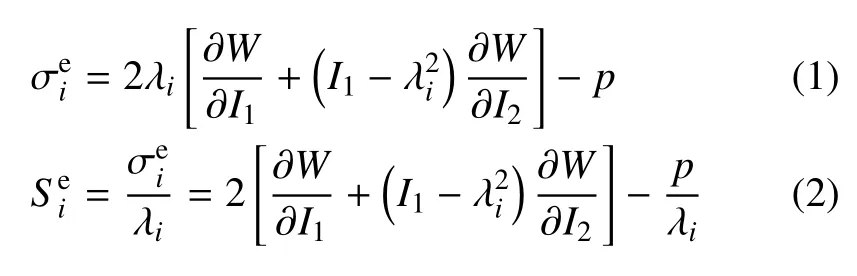
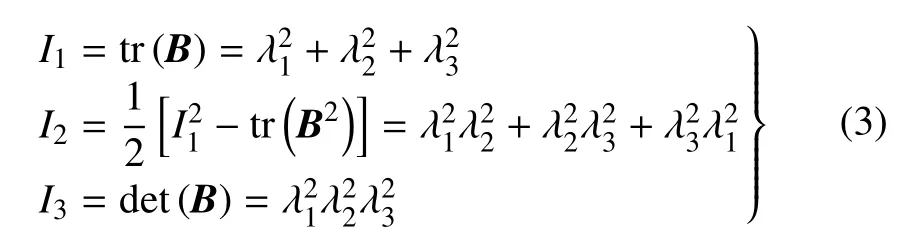
对于不可压缩聚硅氧烷材料,I3=1,W为应变能密度函数,最常见的有多项式应变能密度函数[15-17]和Ogden 应变能密度函数[18].

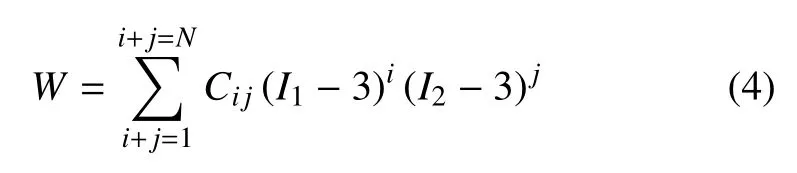
式中,Cij是材料参数,N是多项式阶数.多项式应变能密度函数取不同的低阶项可得到一系列的简化模型.取j=0 可得到Yeoh 模型;取N=1,可得到广义Moony-Rivlin(MR)模型;取N=2,多项式应变能密度函数展开形式如下

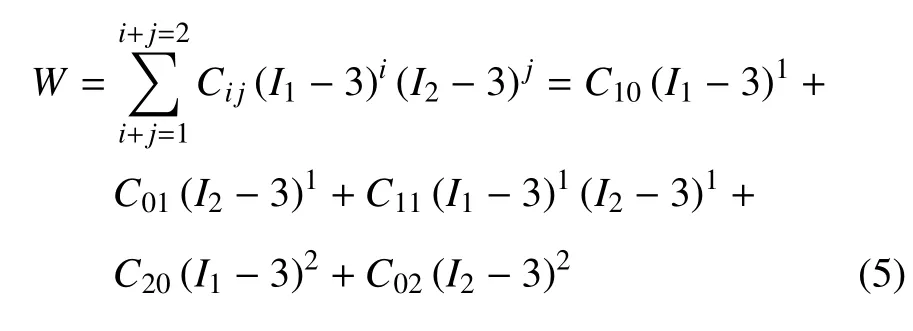
Ogden 应变能密度函数

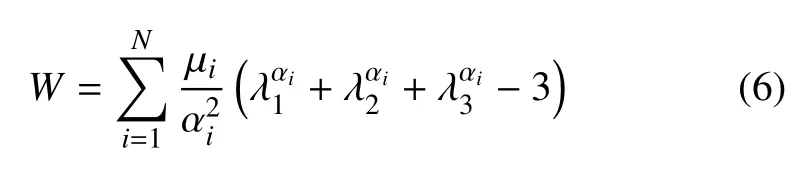
式中,µi和αi是材料参数,N是多项式阶数.

假设方向1 是加载方向,对于单轴拉压[19-20],则有λ1=λ,根据式(2),单轴加载的应力表达式为

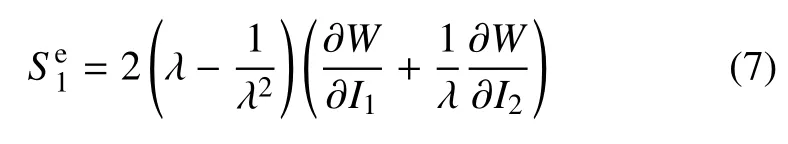
对于平面拉伸,宽度保持原尺寸[19],则有λ1=λ,根据式(2),平面拉伸的应力表达式为

步骤6 一次迭代完成，判断是否达到最大迭代次数gmax，若达到则输出最优解，即得到最优调度作业顺序，否则返回步骤2。

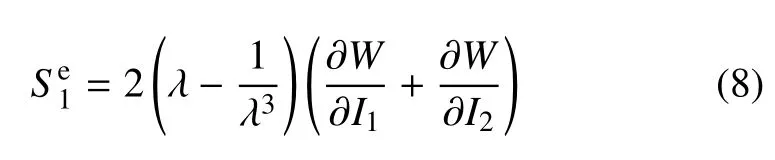
本文采用静态试验数据对聚硅氧烷材料的两类超弹性本构模型进行参数拟合,并选取与试验数据偏差最小的为最佳模型.

1.2 黏弹性模型

麦克斯韦黏弹性本构模型由于模型结构简单,能较精准的表征复杂的线性黏弹性行为而得到广泛的应用,在该模型中,松弛时间常数是描述材料黏弹性特征的重要参数[21-22].Maiti[23]采用10 个松弛时间常数来描述聚硅氧烷材料的黏弹性特性,但在大应变范围下,模型预测结果与试验结果相差较大,因此需要采用更多的松弛时间常数,然而松弛时间常数个数越多,此模型形式越复杂,模型参数也越多,为了确定模型参数需要数量可观的试验.一个好的材料模型应该是用尽可能少的参数去描述材料的实际特性并且没有显著的偏差,因此本文采用非线性黏弹性模型来减少松弛时间常数的个数,即采用函数G(I1,I2) 来代替麦克斯韦黏弹性本构模型中的材料常数Gi[24]

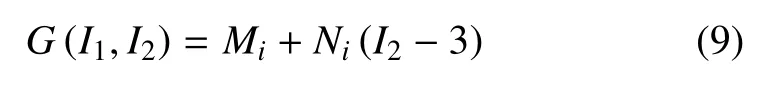
式中Mi,Ni为材料参数.

因此,非线性黏弹性本构关系为

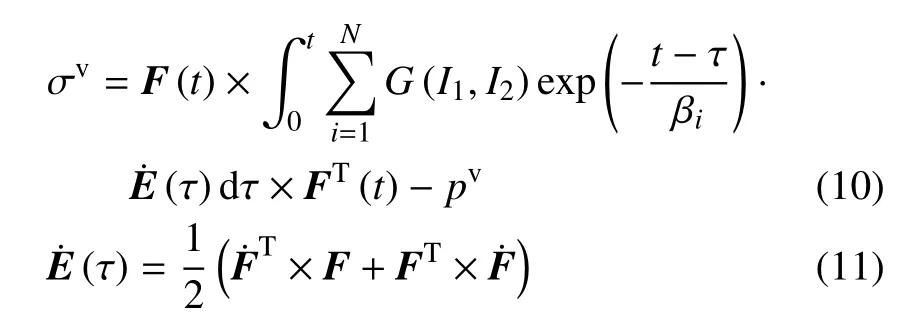
式中,σv是柯西应力(真实应力),pv是黏弹性材料的静水压力,˙E是应变率,F是变形梯度张量,βi是松弛时间常数.

1.3 黏超弹性模型

王锐等[24-25]通过大量试验表明,橡胶类材料在动载荷作用下的总应力是超弹性应力和黏弹性应力的总和,即σ=σe+σv,其中σe和σv由式(1)和式(10)确定.设加载开始的时刻为时间零点,黏超弹性本构模型[24]为

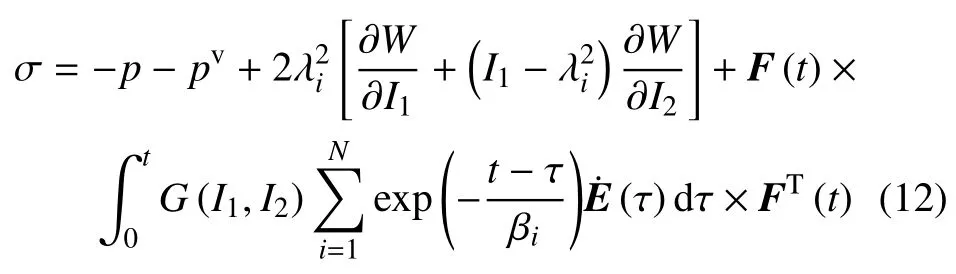
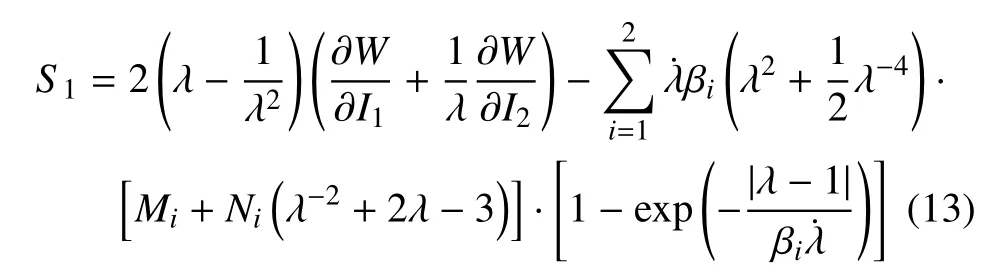
黏弹性模型参数可通过霍普金斯森压杆试验拟合得到.

2 试验与模型参数的确定

2.1 准静态试验与超弹性本构模型参数的确定

2.1.1 试件准备

SE1700 是DOW Corning 公司生产的一种聚硅氧烷硅胶材料,由SE1700 基材、SE1700 固化剂与三丁炔一醇按100:10:1 的比例制成,为使硅胶液能充分填满模具并减少气泡造成的缺陷,使用针筒将硅胶液挤进圆形模具(内径分别为65 mm 和10 mm)中,再放入真空搅拌机抽真空去除气泡,重复操作直至所需厚度,再将其放入固化箱内,设置固化温度为80◦C,固化时间为8 h,固化后密度为1129.96 kg/m3,采用国家标准GB 528—2009 的4 型裁刀切取单轴拉伸试样;平面拉伸试样为20 mm×20 mm 的薄片,厚度1 mm,然而在制作过程中难以保证挤入模具的硅胶质量一致,因此实际厚度会有稍许偏差;单轴压缩试样为厚度约10 mm,直径10 mm 的圆柱.

2.1.2 准静态试验与结果

采用标准的试验方法以及标准试样,对聚硅氧烷硅胶进行了单轴拉伸、单轴压缩与平面拉伸试验,得到不同工况下工程应力与工程应变的关系,从而确定聚硅氧烷硅胶静态本构模型的参数.试验加载速率均为5 mm/min.单轴压缩试验中,硅胶表面涂抹润滑油以减小摩擦产生的影响,待上下夹具均与试样接触时,记夹具间距h0,测试时记录压力F及夹具位移h,名义压缩应力σ 及名义应变ε 分别通过σ=4F/(πD2) 和ε=h/h0计算得出,其中D和h0分别为试样初始直径和高度.平面拉伸可得到在纯剪切条件下的应力应变关系[26].试样与准静态试验结果如图1 所示.

在平面拉伸试验中,试件在高应变下(应变大于3.5)与夹具产生滑移,导致数据可信度不高,并且实际应用中并不考虑高应变情况,因此本文中应变取−0.7～2 (将单轴压缩加载下的工程应力与工程应变取负值[27]).由于多项式应变能密度函数的项数随N呈阶乘式增大,在保证模型精度的前提下,N应取尽量小的值.因此,本文取N=2.将三种工况下的试验数据进行拟合,确定了不同超弹性本构模型的参数,并得到模型结果与试验结果的相对误差.Mooney-Rivlin 模型、N=2 多项式模型、Yeoh 模型、Ogclen三项模型、Ogclen 四项模型的相对误差均方根分别为7.96%,3.90%,8.02%,6.39%和5.12%.C10,C01,C20,C11和C02分别为0.129 2,−0.015 1,0.002 68,−0.005 9,0.002 63 MPa.

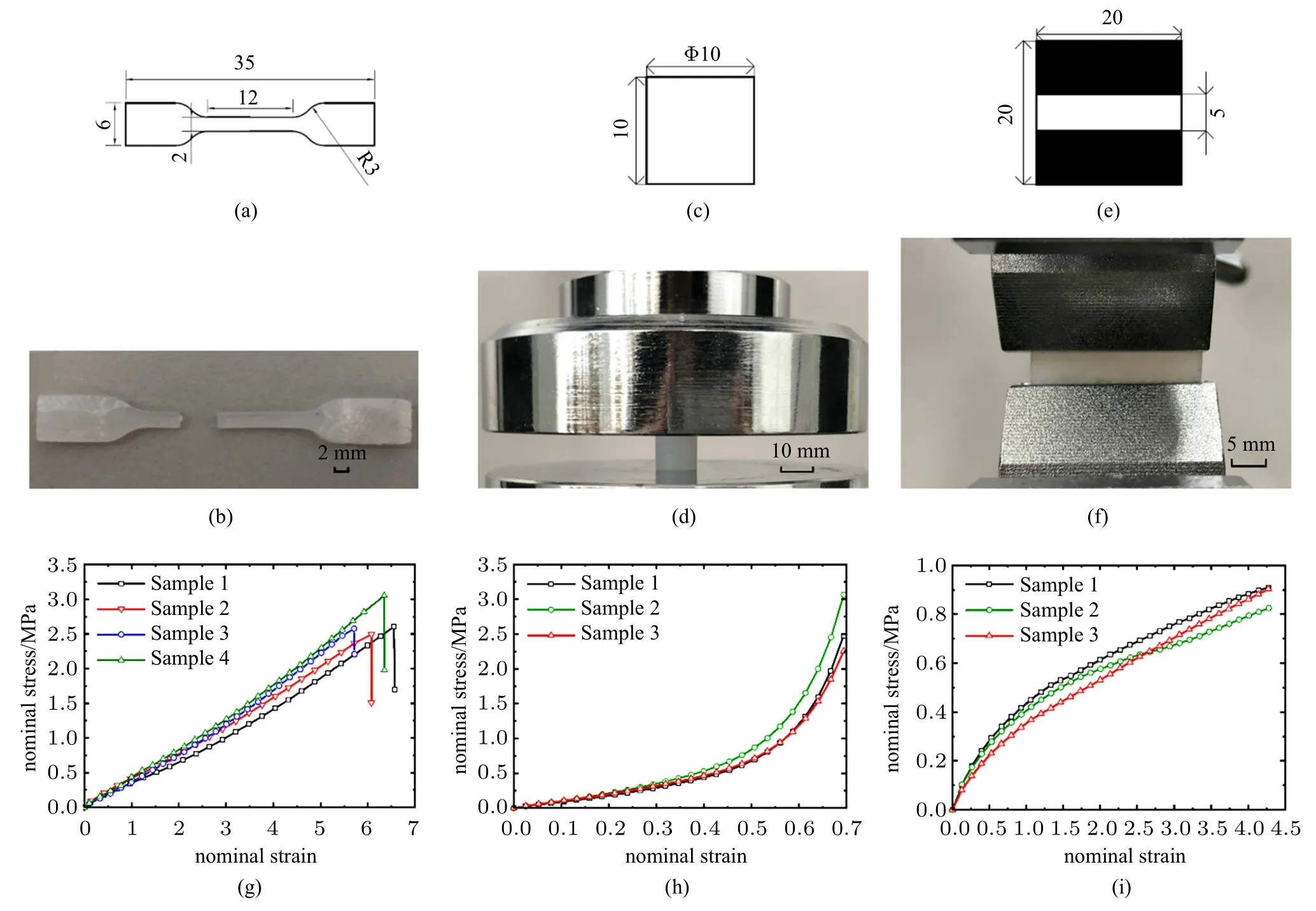
图1 试样尺寸与试验结果:(a)为单轴拉伸试样的理论尺寸;(b)为单轴拉伸断裂试样;(c)和(d)分别为单轴压缩试样的理论尺寸与单轴压缩试验;(e)为平面拉伸试样的理论尺寸,其中黑色区域是夹持部分;(f)为平面拉伸试验;(h),(i)和(j)分别为单轴拉伸、单轴压缩和平面拉伸的试验结果Fig.1 Sample size and test results:(a)Theoretical dimensions of samples before uniaxial tensile;(b)samples after fracture;(c)theoretical dimensions of samples before uniaxial compression;(d)Uniaxial compression test;(e)theoretical dimensions of samples before planar tensile,and the black area is clamping part;(f)Planar tensile test;the results of(g)uniaxial tensile test;(h)uniaxial compression test and(i)planar tensile test data

如图2 所示,四种本构模型都可以较准确地描述单轴加载情况(图2(a)和图2(b)),但对于平面加载情况,N=2 多项式模型精度最高(图2(c)和图2(d)).由于N=2 多项式模型得到的相对误差最小,因此,本文选取N=2 多项式模型来描述聚硅氧烷的静态特征.

2.1.3 准静态本构模型的有限元验证

在求解准静态问题上,一般采用隐式方法,但该方法在计算非线性大变形问题时很难保证计算稳定收敛,因此本文使用ANSYS/LSDYNA 的显式算法来对三种试验进行数值模拟计算.在求解过程中,通过如下方法来使显示求解结果与静态求解结果相近,首先增大加载时长,其次使用光滑幅值曲线的加载方式来避免震荡,最后进行质量缩放.

在对单轴拉伸与平面拉伸有限元仿真中,加载方式与试验相同,模拟结果如图3 所示,从应力云图可以看出,在单轴拉伸下,模型中部区域变形均匀,在单轴压缩下,模型整体变化均匀,在平面拉伸下,模型中部受力均匀,呈现纯剪切的应力状态,有限元分析与试验相符,且数值模拟结果与试验结果相差较小,所以,N=2 多项式超弹性模型可以描述聚硅氧烷的超弹性特征.从能量比值可以看出,变形材料的动能低于内能的5%,所以显式分析结果较为可靠,为探讨不同结构多孔材料的静态力学响应提供了途径.

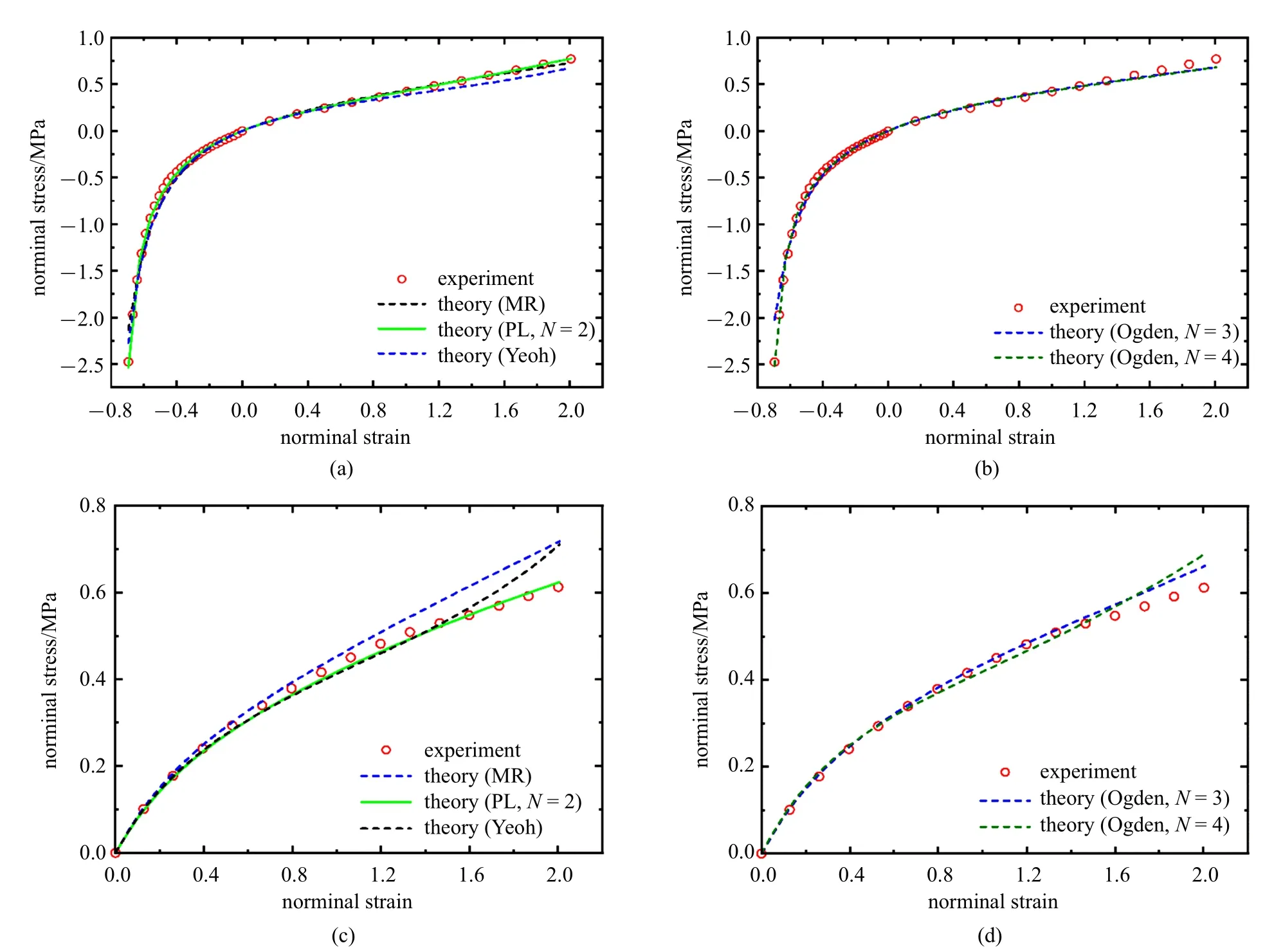
图2 (a)和(b)为Moony-Rivilin 模型、N=2 多项式模型、Yeoh 模型、Ogden 三项模型、Ogden 四项模型对单轴加载试验数据进行拟合后的结果;(c)和(d)为Moony-Rivilin 模型、N=2 多项式模型、Yeoh 模型、Ogden 三项模型、Ogden 四项模型对平面拉伸试验数据进行拟合后的结果.图中MR 代表Moony-Rivilin 模型,PL N=2 代表N=2 多项式模型Fig.2 (a)and(b)The fitting results of uniaxial tests by using Moony-Rivilin model,N=2 polynomial model,Yeoh model and Ogden model;(c)and(d)The fitting results of planar tensile test by using Moony-Rivilin model,N=2 polynomial model,Yeoh model and Ogden model.MR represents Moony-Rivilin model,PL N=2 represents N=2 polynomial model

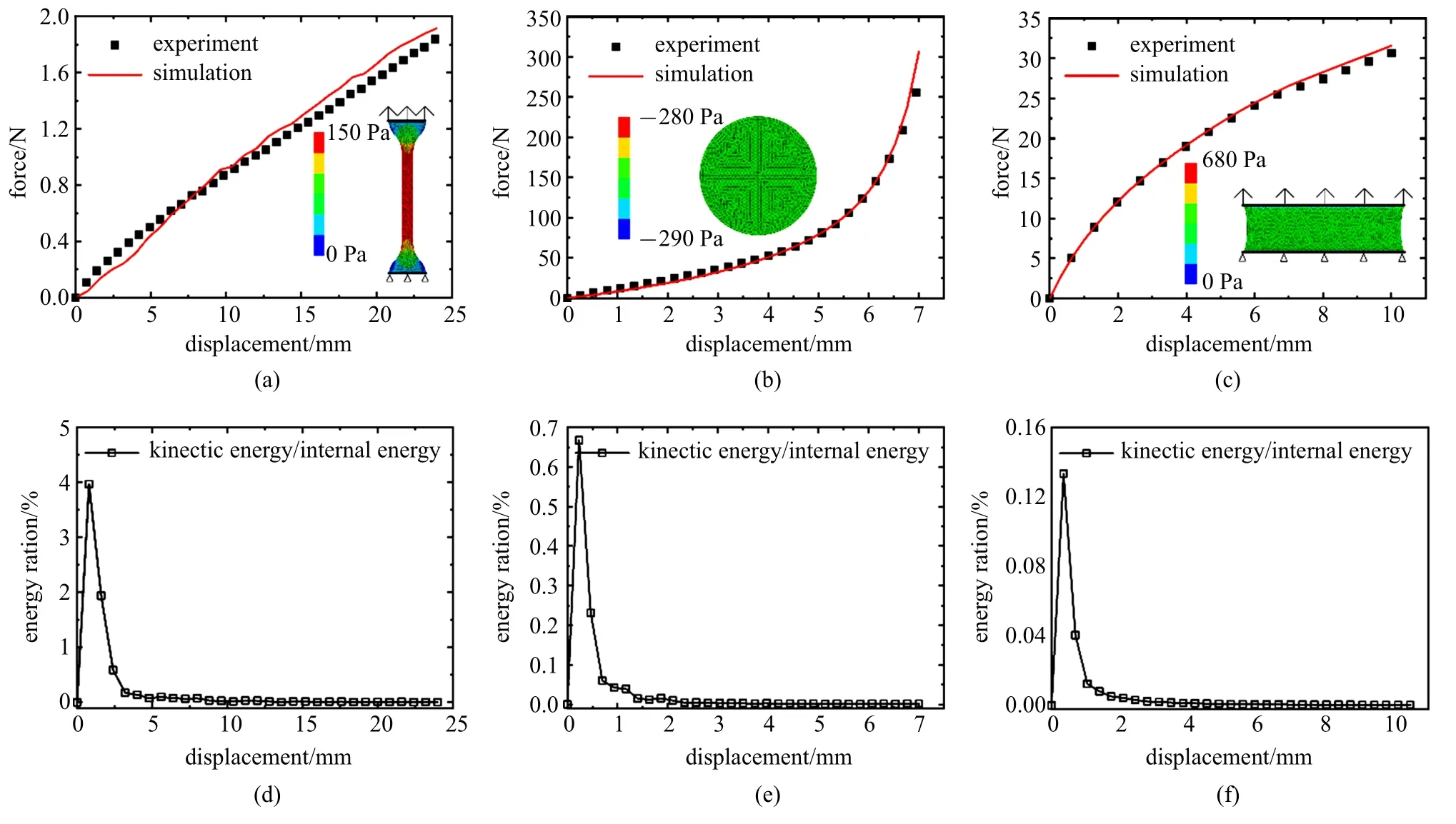
图3 (a),(b)和(c)为试样载荷与位移的有限元分析结果与试验结果.(d),(e)和(f)为单轴拉伸、单轴压缩、平面拉伸中材料的动能与内能的比值Fig.3 (a),(b)and(c)The results by finite element analysis and tests of sample under load and displacement;(e),(f)and(f)ratio of kinetic energy and internal energy of materials under uniaxial tension,uniaxial compression and planar tension

2.2 动态试验与非线性黏弹性参数的确定

2.2.1 霍普金森压杆试验

霍普金森压杆试验装置的系统示意图与装置图如图4 所示.SHPB 装置包括一根撞击杆、一根入射杆、一根透射杆和放置在入射杆和透射杆之间的试样.压杆材料为LC4 超硬铝合金,压杆直径为20 mm,入射杆和透射杆长度分别为2000 mm 和1000 mm,子弹长300 mm.入射杆与透射杆上应变片距试样两端面分别为1200 mm 和500 mm.气枪将撞击杆发射到入射杆上,使冲击杆在冲击面上产生弹性压缩波,弹性压缩波沿着入射杆向试件移动,当弹性压缩波到达入射杆与试件的接触面后,由于材料阻抗差别较大,一部分入射脉冲将从杆−试件界面反射,另一部分将传递给试件.在试件中传递的压缩波将继续沿透射杆传播,直到到达末端.安装在入射杆上的应变片测量入射脉冲(εi)和反射脉冲(εr),安装在透射杆上的应变片测量透射脉冲(εt).

为使应力波在试件内部更快的达到均匀状态,试验中采用直径7 mm,厚度2 mm 的薄片试件[28],并使用灵敏度较高的半导体应变片来获取较低应变率加载下的脉冲信号,同时通过整形器来控制加载速率的变化[29-30].最后,在试件两端涂抹二硫化钼润滑剂以减小摩擦效应给试验结果带来的误差.

试样的平均工程应力,平均工程应变和平均工程应变率可根据应变片记录的信息计算得到,其中,电压信号与应变的转换系数为1 V 相当于1.0×10−3的应变,计算公式如下

式中,E和A分别为入射/透射杆的弹性模量和横截面积,As为试件的横截面积,C0是杆中的应力波波速,εi,εr和εt分别为弹性杆中的入射应变、反射应变和透射应变.

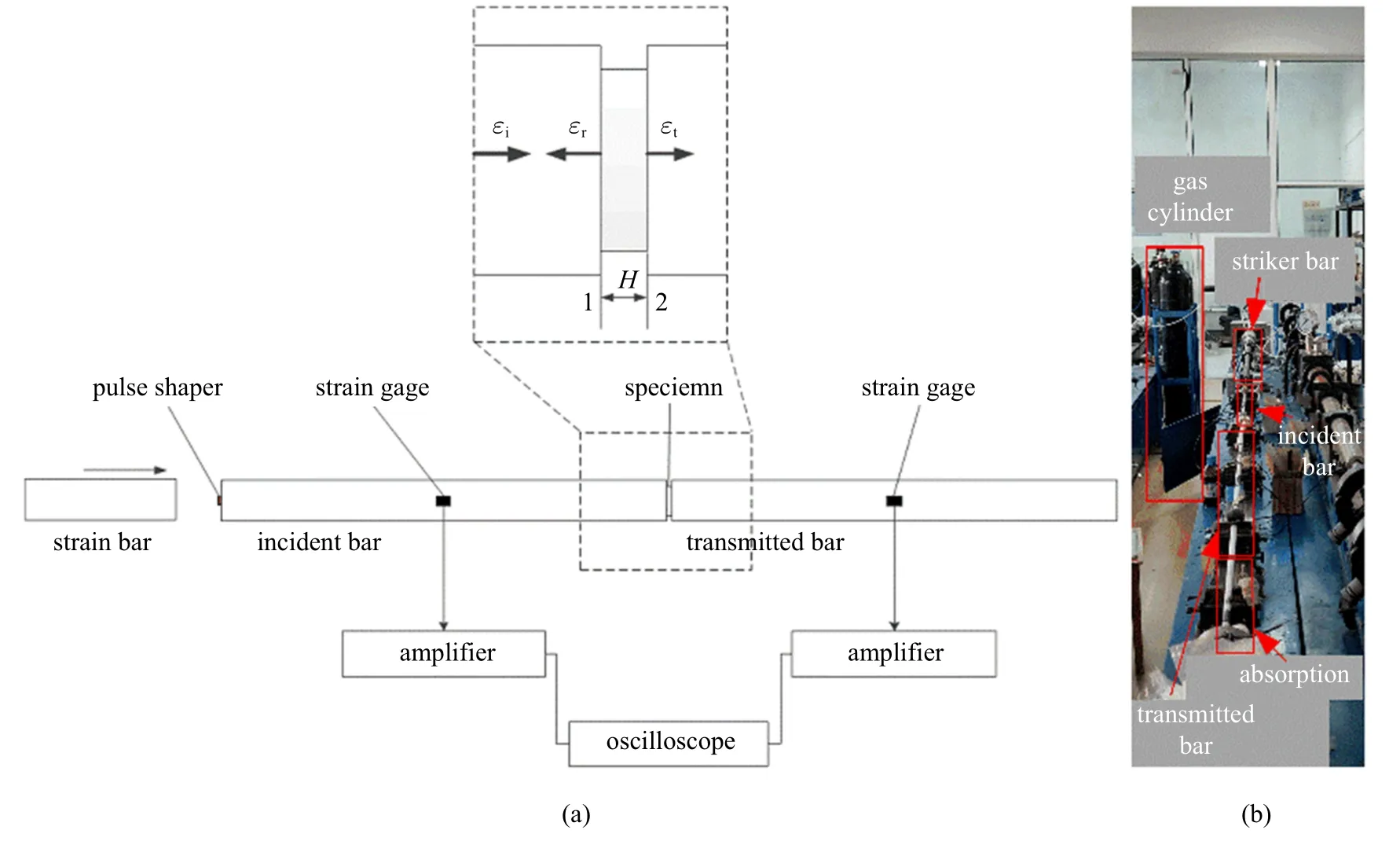
图4 (a)为霍普金森压杆试验装置的简易示意图;(b)为霍普金森压杆试验装置Fig.4 (a)Simple diagram of the Hopkinson pressure bar test device;(b)Hopkinson pressure bar test equipment

2.2.2 试验结果

基于前述测试技术对SE1700 硅胶进行不同应变率的单向压缩测试.从图5 可以看出入射杆和透射杆上应变片实测得到的入射脉冲平稳光滑,透射波信噪比能满足测试精度要求.通过信号计算得到的应变率显示,试验实现了恒应变率加载,数据较为可靠.

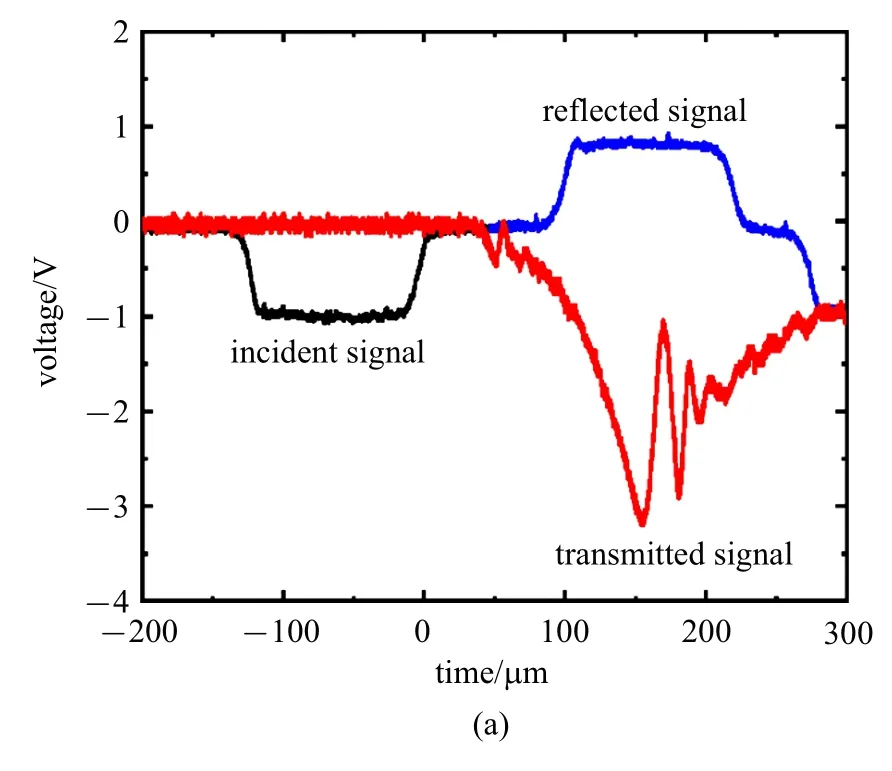
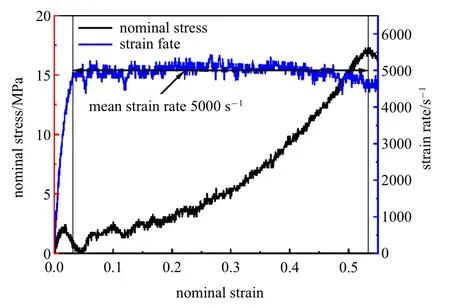
图5 (a)应变率5000 下的入射杆与透射杆应变片记录的脉冲信号;(b)应变率5000 下的应力应变曲线Fig.5 (a)Pulse signal recorded by strain gauge of the incident bar and the transmission bar under the strain rate of 5000;(b)stress-strain curve under the strain rate of 5000

在超弹性材料参数确定的基础上,通过拟合聚硅氧烷硅胶在应变率2050 s−1下的名义应力−名义应变曲线得到黏弹性部分材料参数.图6 是聚硅氧烷硅胶在不同应变率下的应力应变曲线与拟合结果,从图中可以发现,聚硅氧烷硅胶的应力应变曲线具有高度非线性,并存在明显的应变率效应,在准静态下,黏超弹性模型理论曲线与试验曲线一致,证明黏超弹性模型中的假设是合理的;在较高应变率的情况下,聚硅氧烷的杨氏模量随着应变的增大呈现先上升后下降再上升的趋势,其压缩力学响应呈现典型的非线性弹性;随着应变率的升高,模量和定伸长应力均上升,表现出应变率硬化的特征,模型结果和试验结果具有较好的重合性,并且模型结果能很好地体现试验曲线的变化趋势,说明包含两个松弛时间常数的黏超弹性模型能很好地描述聚硅氧烷材料在大应变率跨度内的黏超弹性变形特征.

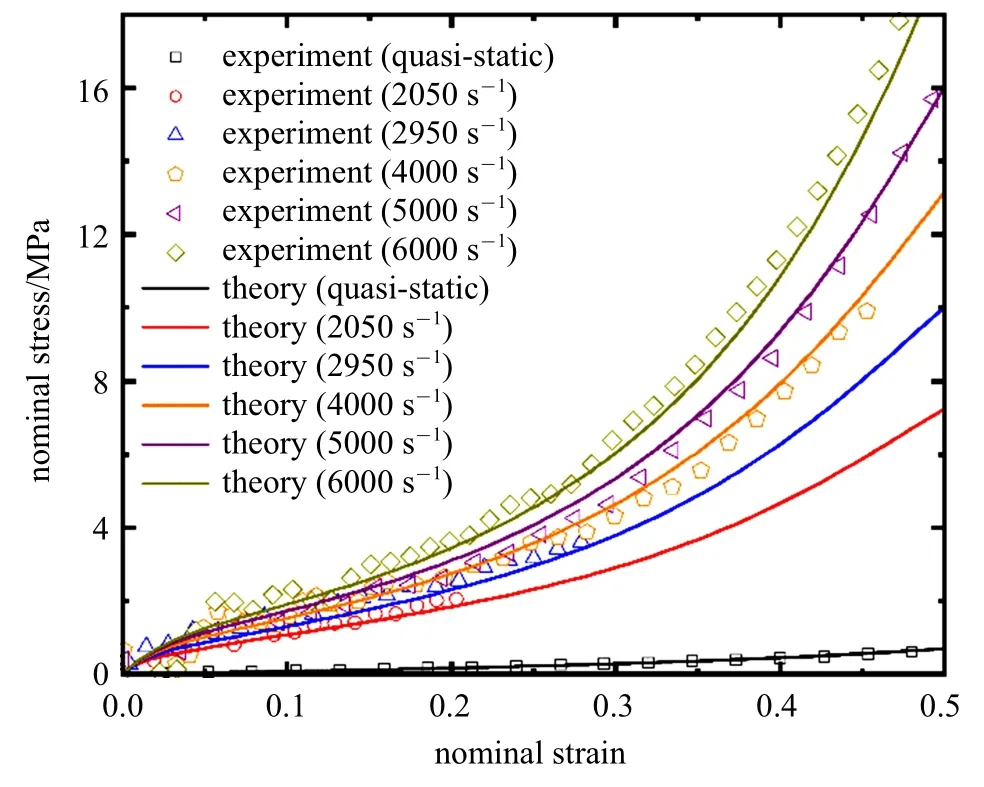
图6 不同应变率下的试验结果与模型拟合结果Fig.6 Test results and model fitting results of samples under different strain rates

3 落锤冲击试验与有限元模拟

为了验证非线性黏超弹性模型的有效性,对聚硅氧烷硅胶圆薄片进行落锤冲击试验,并利用上述模型建立有限元模型对试验结果进行对比.落锤冲击平台与试验参数如图7 所示,加速度传感器和压电石英力传感器分别为一轩YD-128 和YD-3103,并使用控宇UT4004 电荷放大器与优泰UT8516 动静态应变采集分析系统进行信号的放大与采集;聚硅氧烷硅胶圆薄片黏附在铝板上;加速度传感器与力传感器分别记录冲头加速度与试样所受冲击力的电荷信号,并通过电荷放大器进行电荷电压转换,最后将电压信号输出至计算机端;冲头的速度可由下落阶段的加速度与时间数据得到.在有限元分析中,假设铝板与落锤为刚体,设置冲头的速度为1.3 m/s 和2.1 m/s,将聚硅氧烷硅胶在不同应变率下的应力应变输入到LSDYNA 显示有限元分析软件中,为简化计算,取对称的四分之一模型,且均采用4 节点实体单元进行网络划分.

图8(a)和图8(b)是试验数据与有限元分析结果的对比,其中图8(a) 为两种冲击速度下的加速度与时间的对比,图8(b) 为铝板传递到下方力传感器的力对比.由于落锤与试件接触时间较短,并且采集仪对时间进行插值处理,试验数据会存在可变性,与有限元里的时间起点存在一定的差异,但是重复性试验表明,试验结果较为可靠.为了减小时间的影响,将冲头在冲击过程的加速度换算成位移,从而得到力−位移曲线,图8(c) 和图8(d) 为根据上述试验数据得到的力−位移对比图,在两种速度下,有限元分析的力−位移结果与试验结果差异较小,因此数值模拟能较好地描述了聚硅氧烷硅胶薄片在冲击下的变形行为,从而说明非线性黏超弹性本构模型可以用于聚硅氧烷硅胶在不同应变率下的数值模拟分析.

4 结论

(1)本文建立了一个可以描述聚硅氧烷橡胶的非线性黏超弹性力学行为的本构模型,模型的拟合结果和试验结果对比显示该模型能较好地表征大应变和大应变率范围内高弹性和率相关性特征.

图7 落锤冲击的示意图与试验参数:(a)为示意图;(b)为平台图Fig.7 Schematic diagram and test parameters of drop hammer impact:(a)Schematic diagram;(b)platform diagram

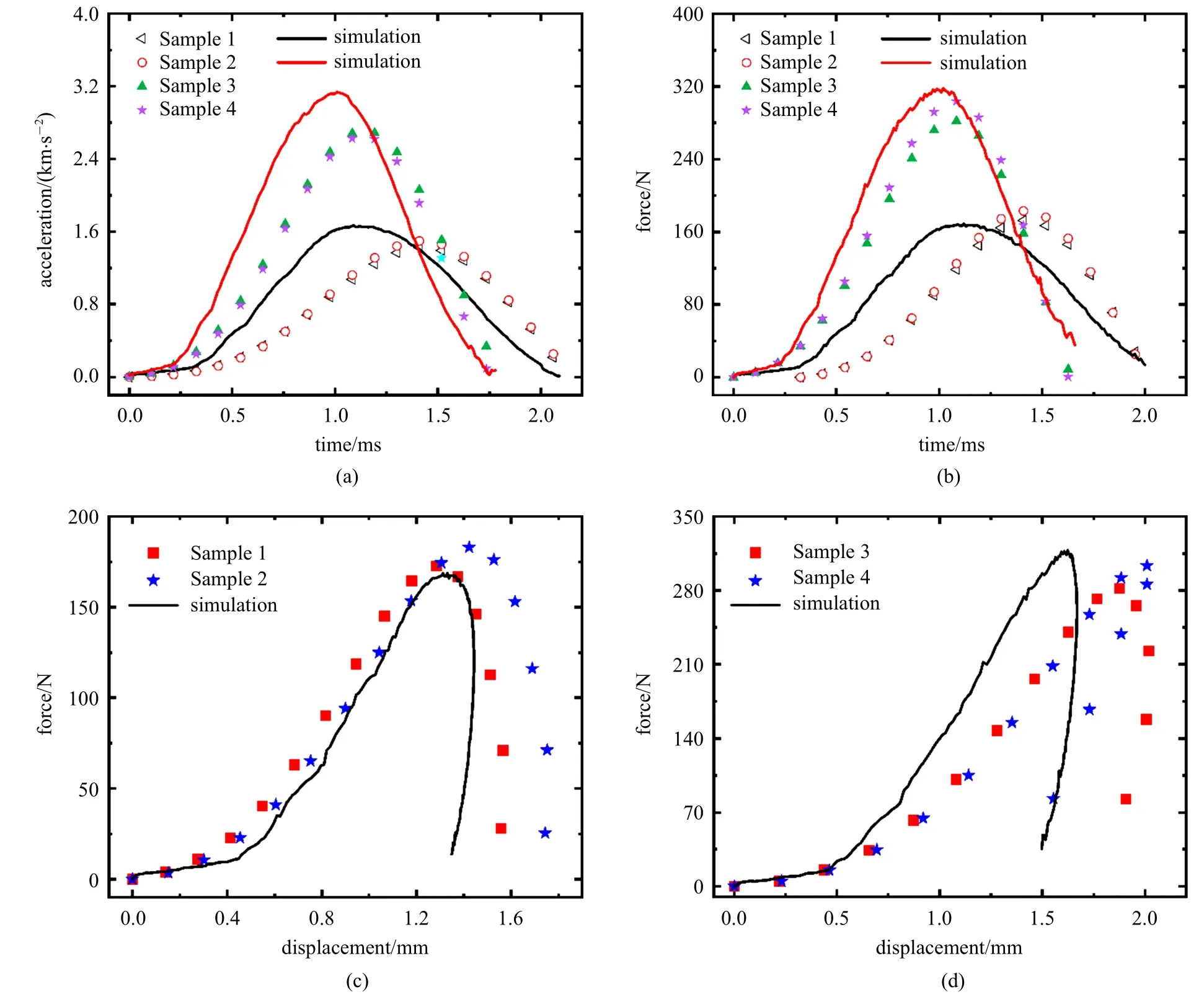
图8 落锤冲击的试验结果与有限元模拟结果的对比:(a)为加速度−时间;(b)为力−时间;(c)和(d)为力−位移Fig.8 Comparison between recorded data and the simulation results of drop hammer impact:(a)Acceleration-time;(b)force-time;(c)and(d)force-displacement

(2)基于非线性黏弹性模型,数值模拟了聚硅氧烷圆薄片的落锤冲击试验,得到在较大应变率范围下,聚硅氧烷硅胶所受冲击力与落锤位移的关系,模拟结果与试验结果吻合较好,因此本文建立的本构模型是有效的,可以用于分析聚硅氧烷硅胶打印的多孔材料在冲击载荷下的动态响应,对多孔材料结构分析优化具有参考意义.

附 录

扫描如下二维码查看用于处理霍普金森压杆试验数据的Matlab程序