高应变率成形极限图测试与仿真研究进展

2021-03-24孟宪举汤秀佳原政军

锻压装备与制造技术 2021年1期

孟宪举，汤秀佳，张莹，原政军

（山东建筑大学机电工程学院，山东济南250101）

1950 年由Clark 和Wood 首次提出应变率敏感材料在高应变率下可增进成形极限能力[1]，从而提升了设计自由度，有利于加工出更加复杂的零件形状[2]。为系统科学的分析高应变率成形极限提高的原因，更好服务于生产，必然需要研究材料的本构关系。当应变率在1000～10000s-1之间时，可以通过霍普金森拉杆实验测量材料力学曲线；当应变率在1～1000s-1之间时，静态和动态变形均同时发生，霍普金森杆实验不再适用，很多研究者利用液压、气动和电磁等加载方式测试材料成形极限能力，以指导实际生产[3-6]。

准静态下可通过标准化的埃里克森杯突实验测量材料在双轴拉伸下的成形极限能力，而高应变率下的杯突实验目前还没有标准化，存在很多问题需要解决。大量实验结果表明单轴状态和低速杯突下的成形极限曲线很难去评价高应变率下的成形性能[6-8]。通过数值仿真模拟高应变率成形过程，可提高分析效率，方便冲压设计，但仿真模型所需要的材料的应变率、应变路径等反映材料性能的参数还需进一步验证。

本文对已有的几种典型的液压、气动和电磁高速杯突实验设备进行了介绍，并对测试的成形极限曲线进行了比较分析；然后对高速杯突仿真模型及仿真结果进行了介绍和分析；最后对高应变率成形极限图测试研究进行了展望。

1 高速杯突实验设备

1.1 液压高速杯突成形

Kim 设计了高速冲击装置，如图1 所示。装置主要包含四个部分：液压助力单元驱动小车、轨道、试件夹持器和减震器，推头通过压缩液体驱动，290kg重的小车沿轨道运动速率达21m/s 并冲向冲头。由于高速冲击中很难精确在试件的破裂位置停止，Kim假设高速冲击实验的破裂时刻与静态冲压实验相似，在冲头夹持盘与座板之间安装了可以调整厚度的阻挡物，因此设备是通过高速物体撞击冲头实现高应变率成形[6]。Kim 分别对CQ 和DP590 两种钢进行了高速杯突实验，冲头直径20mm，试件厚度1.2mm，为了获得多种变形方式下的结果，试件设计成弧形轮廓和不同宽度，检测试件上的印制网格变化，得到应变分布图[2]。

图1 液压高速杯突装置

Nathalie 设计的高速杯突实验设备也是通过液压驱动，实验设备如图2 所示[7]。本实验冲头直径为150mm，利用此设备对厚度1.5mm 的DC01 钢进行了半静态和动态杯突实验。

图2 液压高速杯突装置

1.2 气动高速杯突成形

Engelhardt 等人为解决高应变率下的成形缺乏可重复制造的问题，并推进高速成形极限测试装置标准化，设计了高速杯突实验测试设备[8]。冲头通过高压气体加速，并通过剪切钉保证高压气体在稳定的起始压力下进行冲击，最大冲速达50m/s，冲压部分如图3 所示。实验中通过激光测速，得到随着冲头速度随剪切钉直径增大而增大。

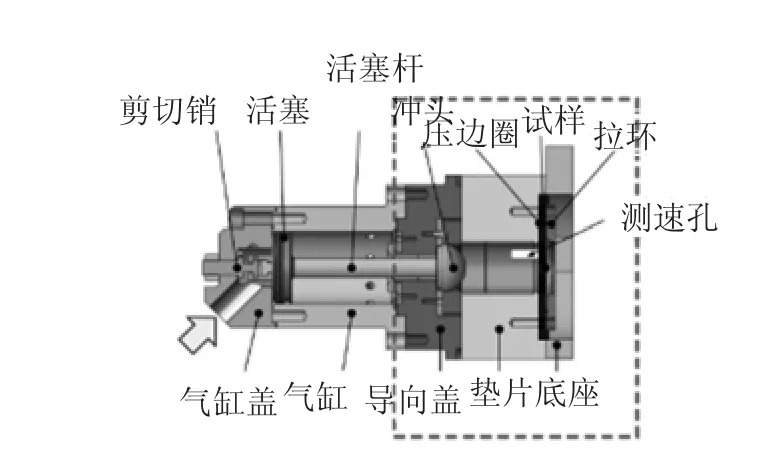
图3 气动高速杯突装置结构示意

江苏大学刘会霞课题组也设计了高压气体驱动的成形装置，对气动高速成形关键装置进行了探索，为研制成形装置提供了指导参考[9]。

1.3 电磁高速杯突成形

为检测多轴拉伸材料性能，Kiliclar 通过电磁高速成形进行了高速杯突实验，实验研究发现高应变率下的拉伸性能得到大幅提升[10]。实验中冲头直径130mm，试件材料为厚度1mm 的铝镁合金和铝合金，试件直径260mm。第一步先深拉50mm，凹模圆角半径20mm，完成材料第一次成形，然后利用电磁高速杯突实现二次成形，凹模半径为10mm。实验设备示意图如图4 所示。

图4 电磁高速成形设备冲头部分

国内学者对电磁成形进行了相应研究，研究多集中在工艺和理论[11]。目前高速杯突成形实验中试件厚度集中在毫米级别[12，13]，更大范围试件尺寸的影响还需进一步研究。而且实验过程中很多状态还不能确切描述，如冲击过程中冲头速度变化及对试件成形的影响，试件破裂位置的准确确定，实验的可重复性均需进一步设计。

2 高速成形极限图测试

Nathalie 通过液压低速和高速杯突实验绘制了材料DC01 的成形极限曲线。结果显示在单轴拉伸区高速成形极限值比低速成形值有所提高，双轴拉伸区低速成形极限值高于高速成形极限值，Nathalie 分析认为实验结果与材料在高应变率下的力学性能有关[7]。

Kim 分别对CQ 和DP590 两种钢进行静态和高速杯突成形[2，3]，汇选试件破裂位置大量点的主次应变绘制了高应变率成形极限图，如图5 所示。通过对比，Kim 得出准静态实验很难评价高应变率下的成形能力。Kim 还对高速杯突实验中的材料的应变率进行了估计，方法是参考静态冲压实验破裂点的位置，根据基于应变率的冲拉过程的有限元分析，提取试件5 个点应变率分布并等价换算确定最终的应变率。

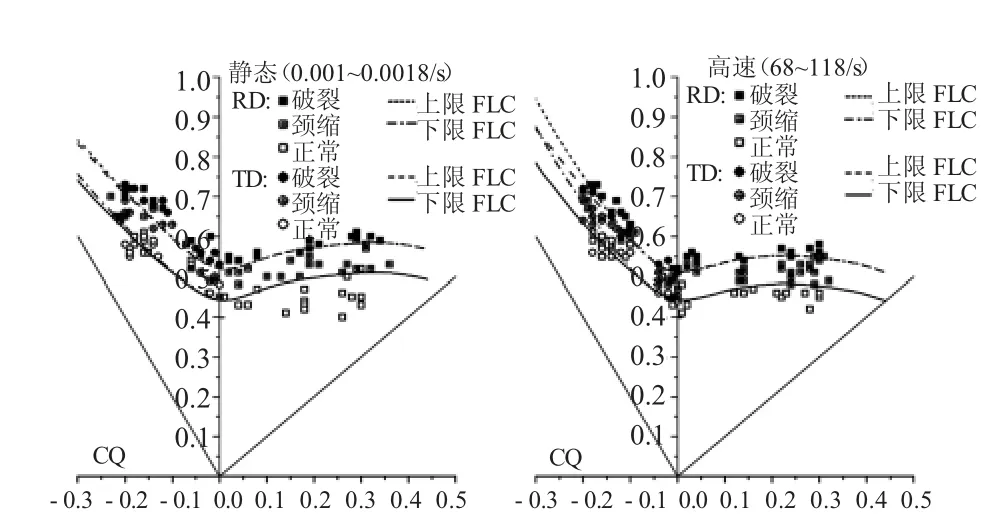
图5 静态与高速成形极限曲线对比

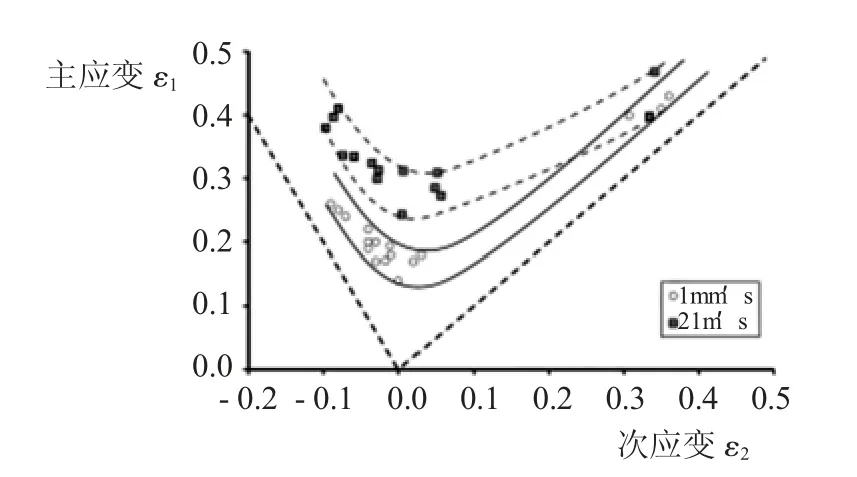
图6 冲头速度1mm/s 和21m/s 下的成形极限曲线

Kiliclar 和Engelhardt 利用气体冲击设备，参考标准进行了杯突实验[8，10]，将实验材料EN A-5083 裁剪成不同的宽度，冲头速度1mm/s 和21m/s，绘制的成形极限曲线如图6 所示，高速下的极限成形曲线比低速下的成形曲线明显提高。Nathalie 的DC01 实验[7]、Kim 的DP590 实验[2]、Korhonen 的AA3104 铝合金和AISI304 不锈钢等实验结果[14]表明高应变率导致了双轴拉伸区成形极限曲线较低，但最大最小应变的极限值确有提高，但要揭示高应变率极限成形的规律还需要更进一步的研究。

3 高应变率杯突成形仿真

3.1 成形极限仿真模型

数值仿真是高速冲压设计的一种重要方法，仿真必须选择合适的模型。很多研究从连续力学角度分析金属成形及破裂过程，在考虑损伤的失稳理论中，基于沟槽缺陷假设的M-K 理论既包含实验结果，在预测成形极限研究中应用较多。李洪周建立了变应变路径条件下材料失稳方程，采用沟槽缺陷假设的M-K 模型对铝合金板进行了成形极限计算[15]。杨晓明建立考虑应变强化和应变速率强化的Fields-Bachofen 本构方程，基于M-K 凹槽理论，预测了铝合金的成形极限曲线[16]。桂良进提出了一种考虑各向异性并以最大凸模力准则作为失稳判据，对高强钢Q490C 的成形极限曲线进行仿真预测的方法[17]。刘健利用最大载荷判断法和应变路径法二者相结合的失稳准则，对板材热拉深成形极限进行数值模拟分析[18]。

仿真模型需要对塑性材料的行为和损伤产生进行了更细致的考虑，Badreddine 提出了高级耦合的连续损伤模型，能反映材料的冲压行为，而且还能描述微观损伤进化过程，预测裂纹产生和扩展[19]。对于压力敏感性材料，Yoon 提出利用不对称的屈服函数，扩充了经典的J2- 塑性参数，在Lode 参数中增加了第三偏差应力不变量，另外各向异性效应又包括了依赖于第二和第三不变量的四阶线性变换张量[20]。Cortese 也遵循这个设想，利用塑性流动的第三不变量，这类模型基于一种假设，即损伤的积累是由三向应力和偏差参数决定的[21]。然而不同应力状态下的合金钢的塑性变形和损伤进行数值和实验结果对比，表明需要对塑性材料的行为需作出更准确的描述。考虑到这些原因，Vladimirov 提出了一种合适的现象学方法，并延伸了塑性破坏[22]。在Pietryga 等人的工作中，进化的四阶张量被用来建模比例加载下的交叉和畸变硬化，这样考虑了塑性各向异性演化与各向同性及运动硬化相结合的问题[23]。

金属板材的破坏受晶粒成核、微孔洞和微裂纹等因素的影响，连续损伤力学可描述损伤随变形演化并最终导致破坏。很多研究利用连续损伤方程，考虑了塑性各向异性和动力硬化，并与各向延性损伤耦合，预测了微裂纹的产生[16，24，27]。如Yue 使用了三类破坏准则：FLD、FLSD 和完全耦合的CDM模型，分析了Al7020 的可成形性[25]。

从本构材料模型的角度看，各向异性粘塑性材料需考虑非线性动力学、各向同性硬化和损伤模型，在高应变率下的成形可能是非线性的应变路径。

3.2 高速杯突数值分析

郭朝选择Johnson-Cook 板料模型，建立了高速冲击下高强度钢DP590 的成形极限图, 模拟验证了Kim 的实验，与实验结果有较好的一致性[26]。

Kiliclar 基于连续力学模型，对铝合金EN AW 6082 T6 进行了高应变率杯突有限元仿真。仿真过程耦合了塑性破坏、非线性动力学和等向同性硬化，通过破坏和粘塑性力学耦合，结合有效应力和等效应变准则，模拟了成形动态过程，并预测了成形极限曲线，与实验结果有较好的一致性[8]。Kiliclar 又将先深冲压技术与后电磁高速成形相结合，利用粘塑性本构模型，各项异性材料模型和延性损伤，应变接近比例路径，仿真了深拉和后续电磁成形，材料参数通过单拉实验并结合反参数识别获取，模拟与实验结果有很好的一致性[10]。

Nathalie 利用Hill48 塑性模型描述材料的流动和屈服，并假设材料变形的应变率独立于应力变化，利用修正最大力学准则判定材料破坏，仿真预测了高应变率成形极限曲线，其中材料属性通过单拉实验获得。预测曲线与实验曲线有较好的一致性[7]。