固体火箭空间快速响应任务规划研究*

2021-03-24蔡应洲贺绍飞谷振丰闫郭伟

现代防御技术 2021年1期

蔡应洲，贺绍飞，谷振丰，闫郭伟

(1.国防科技大学，湖南长沙 410073；2.酒泉卫星发射中心，甘肃酒泉 732750)

0 引言

2002年，美国首次提出“快速响应空间”(operationally responsive space,ORS)的概念，其主要目的是通过发展快速补星能力，保证太空系统受到攻击后仍然能够提供持续可用的空间信息平台，进而使得空间系统具有“弹性”，能够有效规避毁点瘫网式打击[1-2]。快速响应空间以响应时间为第一指标，即要求卫星设计、制造、测试与发射的总时间由传统的数年缩短至几个月，同时对战争、灾害等突发事件的信息支持由当前的几个小时或几天更新一次信息缩短为支持实时信息更新，因此卫星对热点地区的重访周期是其中最为关键的指标[3-4]。考虑快速响应空间的时间要求，ORS计划通常以卫星星座的形式实现。与液体火箭相比，固体火箭具有简单可靠、可长时间贮存、测试发射简单快捷、易于维护等优点，因而成为快速响应空间任务首选运载器[5-6]。我国幅员辽阔，地理环境复杂，各种地震、水灾等突发灾害较多，且随着我国经济全球化的不断深入，海外利益诉求不断加重，同时考虑到我国复杂的周边环境，需要具备对热点地区的应急太空信息支援能力，这对快速响应空间建设和能力生成提出了迫切的需求。

任务规划是指针对某项任务，制定具体计划和指令的过程。成熟的任务规划系统可以极大提高完成任务的效率。目前，我国在空间快速响应任务规划方面的研究相对薄弱，尚未掌握任务规划的流程、方法和关键技术，致使任务组织筹划能力欠缺、资源配置效率低下，因此迫切需要开展空间快速响应任务规划研究，以缩短差距、弥补短板、提升能力。本文以固体火箭空间快速响应任务规划为研究对象，着重研究任务规划的内容、实现方法及流程，为实现固体火箭空间快速响应任务规划能力奠定基础。

1 空间快速响应任务规划总体架构

美军发布的条令文件并未对任务规划(mission planning)相关内容进行定义，但是美军已经研制并投入使用了多款任务规划系统，包括陆军任务规划系统、海军任务规划系统、空军协同任务规划系统和联合任务规划系统等[7-9]。从美军任务规划系统的规划方法和过程看，任务规划主要是在满足一定约束条件的情况下求解任务目标函数最优解的过程。此外，文献[10-13]也对于任务规划，特别是导弹和航天器任务规划，进行了深入广泛的研究。研究认为，任务规划是针对特定任务，在综合分析任务资源、环境条件和安全态势等约束条件的前提下，对任务目标、任务装备、任务时机和行动路线等任务要素进行规划设计的过程。

基于国内外相关研究成果，结合固体火箭航天发射任务实际及其特殊性，将航天应急机动发射任务规划定义为基于上级赋予的空间快速响应任务特性，在火箭、卫星等资源及环境条件和安全态势的约束下，通过计算、分析、仿真等手段，生成任务序列、建立任务方案库并确立最优任务方案的过程。基于上述定义，将空间快速响应任务规划总体架构设计为任务要素分析、轨道规划、弹道规划、机动路径规划、方案评估和仿真演示6个模块。对于空间快速响应任务规划系统，任务要素分析是前提和基础，轨道规划、弹道规划和机动路径规划是核心和关键，方案评估和仿真演示是必要支撑。任务规划系统总体架构组成如图1所示，各模块功能如下：

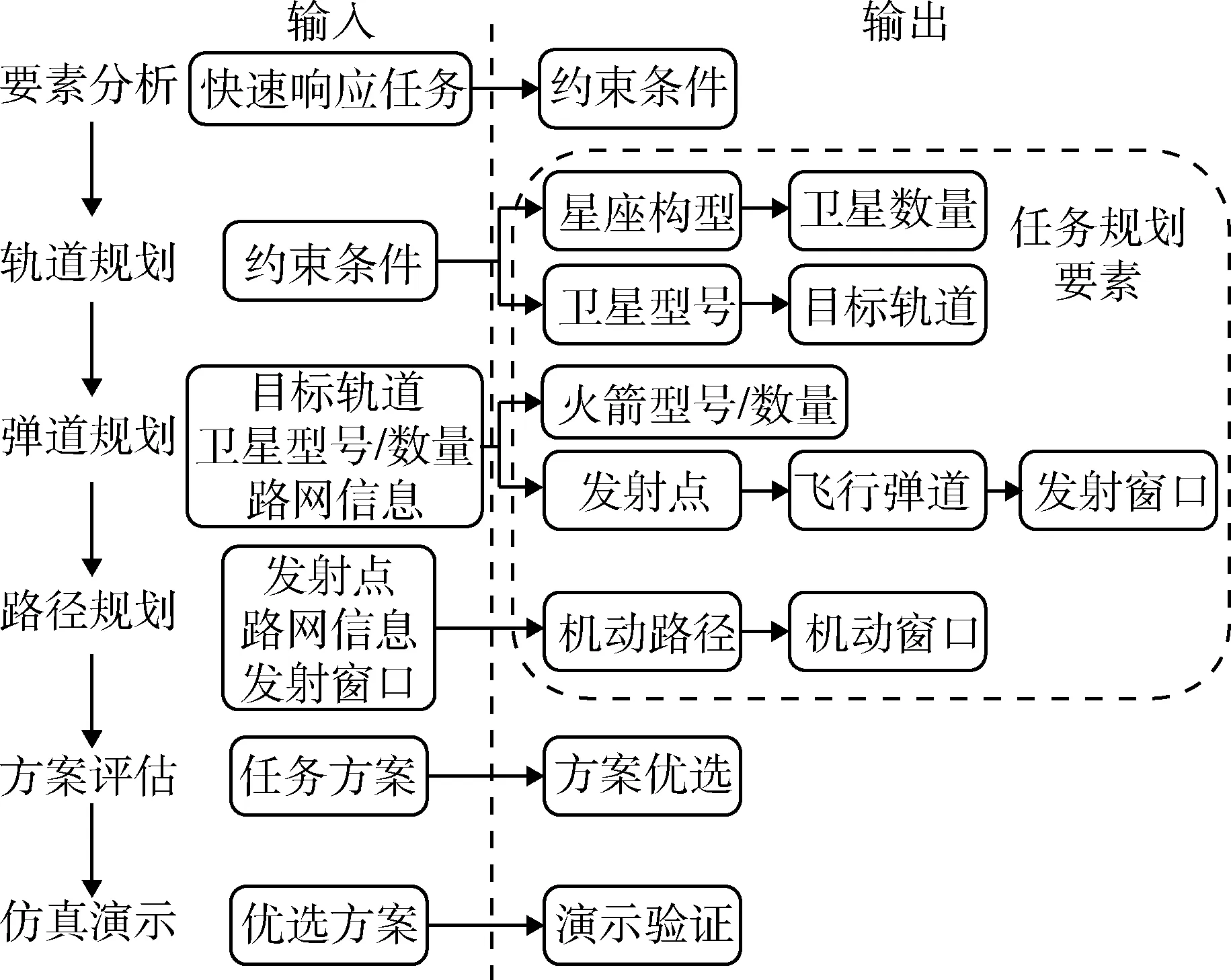
图1 空间快速响应任务规划总体架构图Fig.1 Overall architecture for ORS mission planning

(1) 任务要素分析

任务要素分析主要是针对快速响应任务进行研判、分析，在此基础上明确任务窗口、覆盖性能、目标区域和卫星性能等约束条件。

(2) 轨道规划

轨道规划主要是基于卫星型号数据库，根据覆盖性能、目标区域和卫星性能等约束条件，确定卫星型号、星座构型、卫星数量并开展轨道设计，生成目标轨道库。

(3) 弹道规划

弹道规划主要是基于火箭型号数据库，根据目标轨道参数、卫星型号/数量和路网信息完成火箭选型、火箭数量确定和发射点位选取，进而完成飞行弹道和发射窗口的计算，生成弹道方案库。

(4) 机动路径规划

机动路径规划主要是基于路网和发射点位信息，开展机动路径规划，生成机动路径，并依据发射窗口计算机动窗口，进而生成机动方案库。

(5) 方案评估

方案评估主要是基于任务方案要素，设计构建评价指标体系，进而对任务方案进行评估，完成方案优选排序。

(6) 仿真演示

仿真演示主要是以优选方案为输入，以固体火箭机动、发射、飞行和卫星入轨及在轨运行等过程为典型对象进行仿真模型的构建，进而实现对优选任务方案的全流程演示。

2 空间快速响应任务规划流程

空间快速响应任务规划以空间快速响应任务为输入，以包含星座构型、卫星型号/数量、目标轨道、火箭型号/数量、发射点位、飞行弹道、发射窗口、机动路径和机动窗口等要素的优选任务方案为输出，主要包括任务要素分析、轨道规划、弹道规划、机动路径规划、方案评估和仿真演示6个模块，各模块实现方法及流程设计如下。

2.1 任务要素分析与轨道规划

考虑到ORS计划通常以卫星星座的形式实现，而卫星星座通常由单轨单星和单轨多星组合构建而成，因此，研究卫星星座设计可涵盖所有形式的轨道设计。基于此，设计任务要素分析与轨道规划流程如图2所示，具体流程如下：①根据上级下达的空间快速响应任务，进行要素分析，明确任务窗口、覆盖性能、目标区域和卫星性能等约束条件；②根据卫星性能约束，通过遍历卫星型号数据库进行卫星选型，确定卫星型号；③基于覆盖性能约束和目标区域约束，确定星座构型及卫星数量；④通过构建相关模型，选取合适的优化目标和设计变量，以覆盖性能、卫星型号参数、目标区域经纬度等信息为约束条件，通过智能优化算法进行轨道设计，得到目标轨道集，最终生成轨道方案库(包含星座构型、卫星型号/数量和目标轨道等信息)。

图2 任务要素分析与轨道规划流程图Fig.2 Flow chart of factor analysis and orbit design

对于任务要素分析和轨道规划模块，其核心是轨道设计，关键是模型及优化算法的建立，前提是星座构型的确定。对于卫星星座，其构型通常包括单轨多星构型、单轨单星组合构型、单轨单星与单轨多星组合构型及单轨多星组合构型。通常依据任务的覆盖性能(对地分辨率、重访时间、单次覆盖时间、连续覆盖时间、持续覆盖时间等)要求确定星座构型。星座设计涉及到的模型主要包括轨道动力学模型和覆盖模型，其中轨道动力学模型通常采用解析几何法[14]，覆盖模型通常采用网格法[15]。星座设计是一个多目标多约束优化问题，采用数学模型描述如下[16]：

minF={f1(x),f2(x),…,fs(x)}
s.t.mi(x)=0,i=1,2,…,p,
nj(x)≤0,j=1,2,…,q,

(1)

式中：x为设计变量；fs(x)为目标函数；mi(x)为等式约束；nj(x)为不等式约束；s,p,q分别为目标函数、等式约束和不等式约束的数量。

传统的优化算法无法解决星座设计问题，通常采用智能优化算法进行求解，用于星座设计的典型智能优化算法包括带精英策略的非支配排序遗传算法(non-dominated sorting genetic algorithm-Ⅱ,NSGA-Ⅱ)[17]和多目标粒子群算法(multi-objective particle swarm optimization,MOPSO)[18]，上述2种算法在星座设计中得到了广泛应用。采用智能优化算法进行星座设计，其优化目标通常为星座成本、星座卫星数量和覆盖性能，设计变量通常包括轨道面数、卫星数量、轨道高度、倾角、升交点赤经及卫星相位等。

如前所述，星座设计是一个多目标多约束优化问题，涉及的变量多，需要考虑的约束多，且对于不同的空间快速响应任务，其优化目标通常不同，因此，需要具体问题具体分析，即针对不同的空间快速响应任务，根据其特性，选取合适的优化算法，建立恰当的模型并确定约束条件、设计变量及优化目标，最终完成轨道设计。

2.2 弹道规划

考虑空间系统建设成本约束，同时立足快速响应火箭运载能力实际，对于微纳卫星(1～100 kg)星座，通常采用一箭多星的方式进行部署，而对于小型卫星(100～500 kg)星座则通常采用一箭一星、多箭协同发射的方式进行部署。对于一箭多星部署方式，为了保证卫星寿命，通常采用同轨道面内首颗卫星直接入轨、其他卫星调相入轨方式。调相入轨分为向前调相(调相轨道半长轴低于运行轨道半长轴)和向后调相(调相轨道半长轴高于运行轨道半长轴)，调相轨道半长轴取决于运行轨道半长轴及卫星间相位差，考虑到空间快速响应卫星运行轨道半长轴通常较低，因此，向前调相的调整幅度有限，为了满足快速响应要求通常采用向后调相方式[19]。对于向后调相，忽略调相准备阶段，假设运行轨道周期为Ty，调相轨道周期为Tt，则一个调相周期后卫星向后调整的相位Δu为

(2)

对于一箭一星、多箭协同部署方式，为了提升快速响应能力，通常采用直接入轨方式。考虑到一箭多星发射方式轨道面内首颗卫星采用直接入轨方式，而其他卫星的调相入轨不涉及火箭上升段弹道设计问题，因此，对于弹道规划，可以认为一箭一星、多箭协同方式涵盖一箭多星。

对于一箭一星、多箭协同发射方式，根据固体火箭航天发射任务实际，设计弹道规划流程如图3所示，具体流程如下：

图3 弹道规划流程图Fig.3 Flow chart of trajectory design

(1) 以轨道方案为输入，基于目标轨道和星座构型，对星座中卫星进行编号，根据目标区域约束，计算X号卫星对应的星下点轨迹；

(2) 在发射区域(发射点位的可选区域)内，通过路网数据库寻找卫星星下点轨迹与路网交点，作为备选发射点集(假设固体火箭依托公路进行共面发射)；

(3) 基于火箭型号数据库，以目标轨道和卫星型号/数量为输入，进行火箭选型并确定火箭数量，其中火箭数量决定了发射方式；

(4) 以卫星轨道、发射点、火箭型号参数和落区安全等限制条件为约束，对火箭飞行弹道进行求解，若解存在则进行发射窗口的求解，若解不存在则重复步骤4，以发射点集内的其他发射点为输入重新求解飞行弹道；

(5) 基于火箭飞行弹道计算火箭飞行时间和卫星入轨点，结合目标轨道参数和目标区域位置计算卫星响应时间(卫星自入轨至第一次过顶目标区域上空所用的时间)；

(6) 基于星座构型确定卫星间相位关系，根据任务窗口约束(首次观测目标区域时刻)计算X卫星对应的观测窗口；

(7) 综合火箭飞行时间、卫星响应时间和卫星观测窗口计算发射窗口，若发射窗口实际可行则生成弹道方案(包括卫星编号及其对应的发射点位、飞行弹道和发射窗口等信息)，并将此发射点输入机动路径规划模块作为终端约束进行机动路径规划和机动窗口计算，同时返回步骤4，求解发射点集内其它发射点对应的弹道方案，若发射窗口实际不可行则返回步骤4，以发射点集内的其它发射点为输入重新求解弹道方案，直至遍历发射点集内所有发射点，完成X卫星的弹道方案计算；

(8) 重复步骤2～7计算其他卫星对应的弹道方案；

(9) 考虑到星座卫星间相位相差有限，而卫星在运行轨道的运行速度极快，因此对于不同卫星其观测窗口相差不大，对于同型号火箭，其飞行时间及飞行弹道相差有限，导致发射点位相近的不同卫星对应的入轨点相差不大，卫星响应时间相近，因此，发射点位相近的不同卫星对应的发射窗口相近，相反，发射点位相差较远的不同卫星对应的发射窗口相差较大，考虑火箭协同发射的安全性，需要对所有卫星对应的弹道方案进行安全性筛查，剔除不同卫星发射点位相近的弹道方案，进而生成弹道方案库。

对于弹道规划模块，其核心是弹道求解。运载火箭弹道求解是一类复杂的多阶段、多约束、非线性规划问题，采用数学模型描述如下：

minF(x)=mp，
s.t.h=hm，
v=vm，
i=im，
n≤nmax，
q≤qmax，
Lmin≤L≤Lmax，

(3)

式中：F(x)为目标函数；mp为末级消耗推进剂质量，即弹道设计的优化目标通常为末级消耗推进剂质量最少；x为设计变量，其与飞行程序设计(即火箭型号)相关，通常包括发射方位角、助推段最大攻角、各级飞行段程序角变化率、各级滑行时间和末级工作时间；h=hm，v=vm，i=im为终端等式约束，分别表示入轨高度、入轨速度和入轨倾角满足入轨条件要求；n≤nmax，q≤qmax,Lmin≤L≤Lmax为过程不等式约束，分别表示法向过载、分离动压和落区位置满足飞行安全限制条件。

传统的非线性优化算法(牛顿迭代法、梯度法等)可以求解此问题，但其存在初值敏感、难以全局寻优、计算效率低等问题。由于具有收敛速度快、具备全局寻优能力、初值敏感度低、鲁棒性强等优点，智能优化算法的出现和发展为解决该类问题提供了更优选项。目前，用于快速响应火箭弹道优化的智能算法包括粒子群算法[20]、鱼群算法[21]、遗传算法[22]等。由于不同型号火箭的飞行程序不同，对应的弹道求解模型也就不同，相匹配的优化算法也存在差异，因此，需要针对火箭选型结果，选取恰当的优化算法进行弹道设计。

2.3 机动路径规划

机动路径规划流程如图4所示，具体流程如下：

图4 机动路径规划流程图Fig.4 Flow chart of path planning

(1) 以发射点位可选区域为输入生成路网信息数据库；

(2) 以起始点和弹道方案库中弹道方案的发射点为约束，通过路径规划算法得到机动路径；

(3) 根据机动路径长度和发射车机动速度计算得到机动时间，结合此弹道方案中的火箭发射窗口，计算得到发射车机动窗口，若机动窗口实际可行则生成机动方案(包括机动路径和机动窗口等信息)，若机动窗口实际不可行则返回步骤2，以弹道方案库中其他弹道方案的发射点和发射窗口为输入重新计算机动路径和机动窗口，最终生成机动方案库。

对于机动路径规划模块，其核心和关键是路径规划，其主要包括5个步骤：

(1) 道路建模。道路建模方法包括节点-弧段模型、基于车道的导航模型、GDF模型等，其中节点-弧段模型是道路建模的主流模型。

(2) 路网建模。通常采用分层模型建立路网，即将可用的路网按照通行性和适用性进行层级划分以提高路径搜索效率，例如考虑到火箭发射车通行能力要求，构建2层路网：第1层为高层网络，主要为铁路网；第2层为底层网络，主要为三级以上公路。

(3) 制定搜索策略。搜索策略依据路网模型而制定，对于分层路网模型常用分层搜索策略，即设定路段长度阀值，若发射点和起始点之间的距离超过阀值则优先在高层网络搜索路段，而后在低层网络搜索路段，两者共同组成最短路径；若发射点与起始点之间的距离未超过阀值则直接在低层网络搜索最短路径。

(4) 确定约束条件。对于机动路径规划，其约束条件主要包括2个方面：一是静态约束，对于铁路机动，需要考虑隧道尺寸对于通行的限制，而对于公路机动，则需要考虑桥梁、隧道、道路转弯半径和交叉路口转向对于通行的限制；二是动态约束，主要考虑路网动态通行性，即是否存在自然灾害、人为破坏或交通事故导致的路网临时不通的情况。

(5) 选择搜索算法。在路径规划方面，启发式A*算法[23]及其改进算法[24]由于具有高效的搜索效率，因而被广泛应用，可有效解决路径规划问题。

目前，商业路径规划软件已经较为成熟，其中不乏优异的路径规划算法，具有搜索效率高、精度高等优点，但其并未考虑发射车载箭机动的约束条件，后续可以借鉴商业软件成熟科学的算法同时考虑发射车载箭机动特定的约束条件，进而开发适用于航天机动发射路径规划的方法。

2.4 方案评估

通过任务要素分析和轨道规划可得到轨道方案库，对于轨道方案库内的每条目标轨道，通过弹道规划和机动路径规划可得到多个弹道方案和机动方案，通过计算轨道方案库内的所有目标轨道最终生成弹道方案库和机动方案库，进而生成包含轨道方案、弹道方案和机动方案的任务方案库，用于方案评估。方案评估流程如图5所示，具体流程如下：①根据任务方案组成要素选取适当指标构建指标体系并确定指标权重；②对任务方案库中方案进行指标量化；③选取适当的评估方法，对方案进行评估，依据评估结果对任务方案进行优选排序。

图5 方案评估流程图Fig.5 Flow chart of project evaluation

对于方案评估模块，其基础和前提是评价指标体系的构建，核心和关键是指标赋权方法和评估方法的选取，其中指标体系的构建需要遵循完备性(评价指标体系涵盖用于评估任务方案效能的所有指标)和独立性(构建的评价指标之间应当相互独立，不存在重复)等原则；指标权重的确定通常选用组合赋权法[25]，即将主观赋权法和客观赋权法按照一定的配比进行组合，进而对指标进行赋权，其中层次分析法是最具代表性的主观赋权法，信息熵权法是常用的一种客观赋权法；TOPSIS(technique for order preference by similarity to ideal solution)算法[26]作为一种综合评价排序方法可用于任务方案优选排序。目前，伴随智能算法[27-28]的发展，其在评估优选中的应用是一个发展趋势。