一种高超声速飞行器在线反馈滤波算法*

2021-03-24高长生王越欣荆武兴胡玉东

现代防御技术 2021年1期

高长生，王越欣，荆武兴，胡玉东

(哈尔滨工业大学航天学院自主空间系统实验室，黑龙江哈尔滨 150001)

0 引言

临近空间是指距离地面高度为20～100 km的空域，该空域处在航空和航天之间，比卫星飞行高度低，比飞机飞行高度高，探测信息相对空缺，掌握该空域对取得制空权有很大的作用，临近空间特殊的战略地位对未来战争体系的影响不可估量[1-3],近年来得到了各国军方的高度重视。以美国为代表，如HTV2，CAV等高超声速飞行器，其高速、远程、精确的特点可以实现全球战略打击目的，给其他国家的国防带来了严肃的考验[4-5]。在此背景下，针对该类飞行器的拦截研究已迫在眉睫。

在解决临近空间目标跟踪问题时，一个重要的方面就是构建高超声速飞行器的运动模型，经过近几十年各国科学家和学者的深入研究，其相关理论和模型日趋完善。相关的运动学模型主要有：匀速模型(CV)，状态量只有位置和速度2方面，适合跟踪目标作简单的匀速直线运动，无任何机动情况下的运动形式[6]。匀加速模型(CA)，相较于匀速模型，把目标的加速度加入到状态量中，适合跟踪目标作匀加速运动对应的跟踪模型[7]。圆周转弯模型(CT),指物体的速度和加速度大小均不变化，只有方向改变，主要用于跟踪目标转弯，常用于描述二维运动状态[8]。上述模型均是将加速度假设为高斯白噪声系统，这在实际应用中会出现很大的误差，此外一阶时间相关模型(Singer)，将目标的加速度作为具有零均值指数衰减自相关函数的随机过程，且具有指数自相关的特性，弥补了这一假设误差[9]。在此基础上，国内的周宏仁教授对Singer模型进行了改进，认为下一时刻的加速度不能随意取值，只能在当前加速度的领域内取值，目标加速度的统计特性用修正的瑞利分布来表示。在目标运动过程中实现了加速度均值自适应变化，并且加速度概率分布与均值相关，方差则由加速度均值决定。目标的加速度只能在前一时刻加速度的邻域范围内变化，建模为非零均值的自相关指数衰减过程[10]。

在高超声速飞行器跟踪系统中，工程上应用最为广泛的是卡尔曼滤波。应用卡尔曼滤波算法完成系统状态估计，需要依赖构建的系统模型和实时的测量数据。然而，在跟踪未知临近空间目标时，飞行器的运动规律及参数无法得知，必然会引起跟踪模型的不匹配问题，同时目标运动过程中随时可能存在机动模式切换情况[11]。目标运动的不确定性严重影响了算法的精度和稳定性。目标机动运动实质上是一种非线性现象，可以利用神经网络的强非线性映射能力对目标运动的不确定性建模，对目标机动在线辨识，实时修正滤波估计值[12-14]。BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络，是应用最广泛的神经网络，可以利用BP神经网络对滤波算法的滤波误差进行预测，并补偿给滤波估计值，从而提高滤波精度[15]。

综上所述，本文针对高超声速飞行器难以进行高精度跟踪这一问题，提出了一种高超声速飞行器在线反馈滤波算法。在当前统计模型的基础上，利用BP神经网络与卡尔曼滤波相结合进行滤波器设计，实现对高超声速飞行器高精度跟踪。最后采用数学仿真手段对所提出的算法进行了验证，并进行相关分析。

1 运动学跟踪模型与量测模型

1.1 运动学跟踪模型

目标跟踪模型是跟踪算法的基础，是系统的状态方程部分，即当前时刻目标的状态量由前一时刻状态量的表示方法，目标的运动特性由位置、速度、加速度等状态量表征。

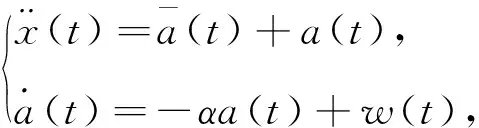
(1)

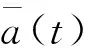
(2)

假设红外采样间隔为T，对上述方程离散化，则离散时间状态方程为

(3)

式中：X(k)为k时刻目标运动的状态量;F(k)为状态转移矩阵;G(k)为输入控制矩阵；W(k)为噪声。

状态转移矩阵F(k)的表达式为

(4)

输入控制矩阵G(k)的表达式为

(5)

当前时刻的加速度均值一般情况下难以确定，用滤波递推过程中的加速度一步预测代替，有

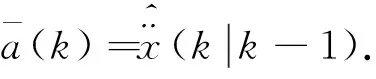
(6)

目标当前加速度方差估计：

(7)

式中：amax和a-max分别为目标加速度的最大值和最小值。

噪声W(k)的协方差为

(8)

Q为对称矩阵，而且有

(9)

综上，“当前”统计模型将上一个时刻的加速度输入到当前时刻来估算加速度方差，进而自适应地调整过程噪声。

1.2 量测模型

首先定义探测坐标系OxPyPzP，简记为P。OyP轴在探测系原点水平面内，指向北极方向，OzP轴垂直于水平面指向上方，OxP构成右手坐标系，坐标系固连在地球表面。如图1所示。

设目标在探测系下的位置矢量：

r=(x,y,z).

(10)

红外探测器基点在探测系下的位置矢量：

Si=(xi,yi,zi).

(11)

目标在本体系下的矢量为

(12)

所以有

(13)

如图2所示。

图2 定位原理Fig.2 Positioning principle

定位：

(14)

整理为矩阵形式：

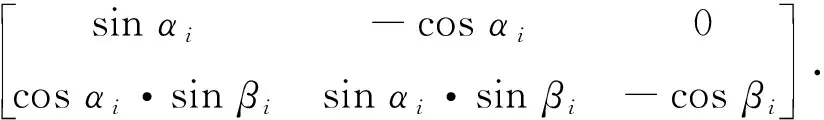
(15)

则有

(16)

综上，使用最小二乘算法定位，则有

M·X=Y⟹X=(MT·M)-1·MT·Y.

(17)

2 基于BP神经网络的滤波器设计

2.1 BP神经网络

BP神经网络由3部分组成，分别为输入层、隐含层和输出层，其中输入层接受外界信息和数据输入，输出层则输出网络对输入信息和数据的处理结果，隐含层作为输入层和输出层的媒介，完成信息和数据的分析、处理过程。如图3所示。

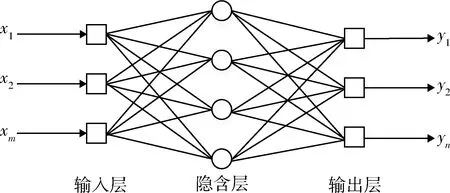
图3 BP神经网络基本结构Fig.3 Basic structure of BP neural network

神经元作为人工神经网络中信息、数据处理的独立单元，主要完成3个功能：加权、求和以及激活，其模型如图4所示。

图4 神经元模型Fig.4 Neuron model

(1) 加权：接受前一层传来的数据，并且每一个输入信号都对应一个不同的权重；

(2) 求和：确定全部输入在不同权重下的组合效果；

(3) 激活：将数据的加权和输入到激活函数，并将函数输出结果传递给下一层。

激活函数采用tansig函数，可以将一个实数映射到[-1,1]区间内，表达式为

y=2/[1+exp(-2x)]-1.

(18)

如图5所示。

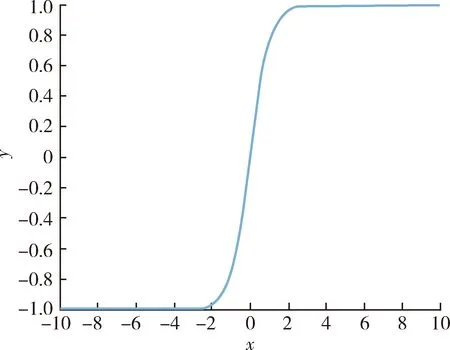
图5 tansig函数Fig.5 Tansig function

2.2 混合滤波器设计

将BP神经网络的学习和适应能力应用到卡尔曼滤波中，使滤波器兼备学习能力和估计性能，从而提高系统的跟踪性能。

输出滤波器的状态估计方程为

(19)

将估计方程做等价变形，有

(20)

图6 算法原理Fig.6 Algorithm principle

2.3 算法流程

(1) 网络结构与参数配置

X=[xyzvxvyvzaxayaz].

(21)

状态估计9维，残差3维，增益为9×3=27维，则输入节点数为39个，输出节点数为9个。本文设置隐含层为2层，节点数分别为45，9。学习率采用Levenberg-Marquardt算法。

(2) 采集训练数据集

本文采用有监督学习的方式离线训练网络，典型弹道及一些常见的机动弹道等弹道的跟踪结果进行数据采集，包含15 000个输入输出时间序列数据。

(3) 数据预处理

BP神经网络的激活函数将数据映射到(-1,1)，需要对输出数据进行归一化处理，考虑到神经网络的输入数据之间存在很大的量级差别，为了避免因量级差异引起网络误差预测较大，需要对输入数据进行预处理。采用最大最小值方法进行数据归一化。用神经网络得到的预测结果还需要进行数据的反归一化处理，反归一化是归一化的逆过程。

(4) 网络训练

设置网络最大训练次数为3 000，训练精度为1×10-5，是输入输出数据归一化后的精度要求。设置隐含层的激活函数为tansig函数，输出层的激活函数为purelin函数。

(5)卡尔曼BP神经网络融合输出

将训练好的BP神经网络嵌入到卡尔曼滤波器中，形成混合滤波器。在对机动目标状态估计时，经过卡尔曼滤波得到网络的输入数据，需要一步数据归一化处理。而后将归一化数据输入网络得到输出数据，需要输出数据反归一化处理，得到网络预测的估计误差。

同时需要对网络的估计误差设置阈值检测，若估计误差超过阈值限制，则认为此次的网络预测值错误，对滤波估计值不进行修正。即：

(22)