信号处理课程中的卷积运算与MATLAB 仿真设计

张广顺 盖琦 蔡锋涛 杨迎接

(天津理工大学中环信息学院,天津 300380)

0 引言

卷积运算是信号处理与系统分析课程中极为重要的一种数学运算,对于连续信号,需要求积分,也称卷积积分;对于离散信号,需要求和,也称卷积和[1]。但由于教材中对于卷积的定义通常拘泥于形式,使学生感觉难以理解,学习起来比较困难,影响了学习效果。事实上,卷积也可称之为“加权平均积”,卷积的离散形式便是人人会用的加权平均,而连续形式则可考虑为对连续函数的加权平均。卷积定理表明,对信号在时间域做卷积运算,相当于在频率域做滤波处理。M A T L A B 是目前广泛使用的科学计算软件,应用M A T L A B 软件编程实现卷积的计算过程,可以帮助学生更好的理解卷积的意义和计算过程,激发学生的兴趣,提高学习质量[2]。

1 卷积的定义

1.1 卷积积分

设 f1(t) 和 f2( t) 为定义在 ( -∞, +∞) 区间上的两个一维连续时间信号,定义积分运算如式(1)所示:

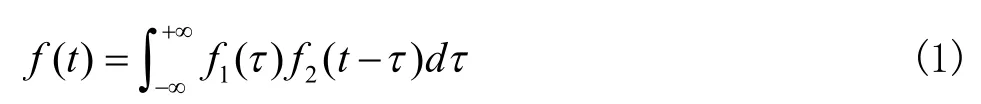
称 f ( t) 为 f1(t) 和 f2(t) 的卷积积分,简称卷积,用*代表卷积运算,表示为[1]。

1.2 卷积和

设 f1(n) 和 f2(n) 为定义在 ( -∞, +∞) 区间上的两个一维离散时间信号,定义求和运算如式(2)所示:

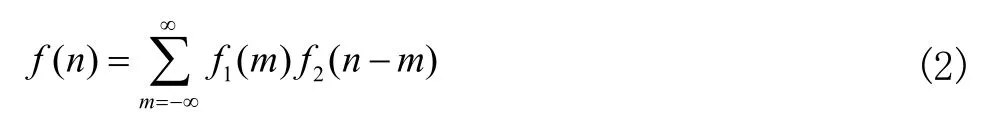
称 f (n) 为 f1(n) 和 f2(n) 的卷积和,简称卷积,用*代表卷积运算,表示为

1.3 计算步骤

根据卷积的定义,计算过程可分为四步[3]:(1)换元;(2)反转、平移;(3)相乘;(4)求积分(或求和)。由于卷积的结果是关于t(或n)的函数,所以当t(或n)取不同值时,卷积结果是不同的,而t(或n)代表的是平移的量。

卷积的物理意义是,任何信号都可以表示成信号本身和单位冲激信号的卷积,不同的信号都可以分解成相同的形式,在分析线性时不变系统时,可以应用卷积运算来求解系统的零状态响应。

2 MATLAB仿真

2.1 卷积计算

下面以连续信号为例,编写MA TLA B代码,计算两个信号的卷积。设,要求画出 f ( t )的波形图[4]。

根据卷积积分的计算过程,卷积的结果实际上是让一个信号 f1(τ) 保持不变,另外一个信号 f2(τ) 先做反转得到f2(-τ) ,然后让 f2(-τ) 在时间轴上做平移,从左往右穿过第一个信号 f1(τ) 所覆盖的区域,平移的量记为t,则卷积的结果就是两个信号重合部分的面积,是关于t的函数。为了能够清楚的表示两个信号之间的相对位置及计算结果,编写MATLAB代码,把两个原始信号的波形及计算过程中两信号的相对位置的变化用动画的形式演示出来,结果如图1所示,其中(a)～(f)分别表示平移t取不同值时,两信号的相对位置。

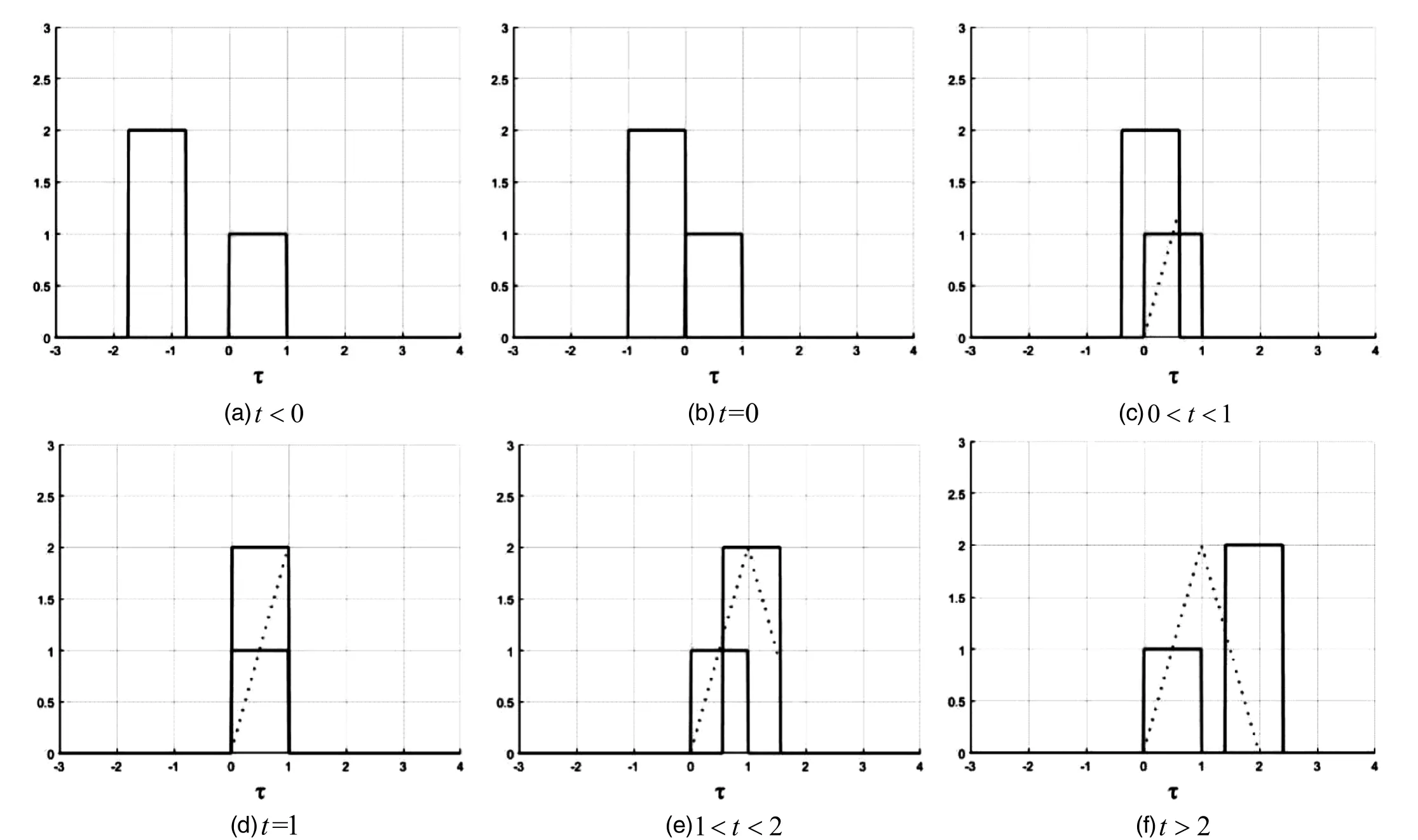
图1 卷积过程演示Fig.1 The convolution process

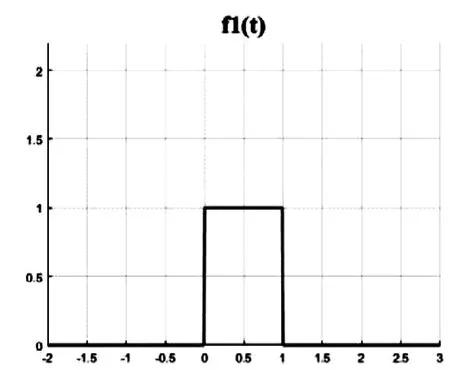
图2 f (t)波形图Fig.2 f1(t) waveform

图3 f 2(t)波形图Fig.3 f2(t)waveform

图4 f (t)波形图Fig.4 f3(t) waveform

同时,把三个信号的波形图分别显示,结果如图2～图4所示。

对于离散信号,在MATLAB 中提供了计算卷积和的函数conv,此函数可用于计算两个起始位置在原点的信号的卷积和[5]。

2.2 卷积滤波实例

下面以声音信号为例,编写MA TLA B代码,通过对纯净的语音信号加噪声,再做卷积运算实现去噪[6]。

调用函数audioread读入一纯净语音信号,语音内容为古诗“人闲桂花落”,记为 x ( n) ;噪声选择为一单频正弦波,将语音信号与噪声信号叠加,得到,画图观察波形图的变化,如图5所示,并调用sound函数,播放声音,体会加噪前和加噪后两段声音的区别,可以听到加噪后的声音信号中有明显的干扰音。

为了实现去噪,我们选择了两种方法:(1)调用conv函数,选择信号,计算;(2)调用filter函数,用 h( n) 作为滤波器,对 x '( n) 做滤波处理。

经过两种方法处理后,分别画出处理后信号的波形图,并播放处理后的声音信号,结果如图6所示。

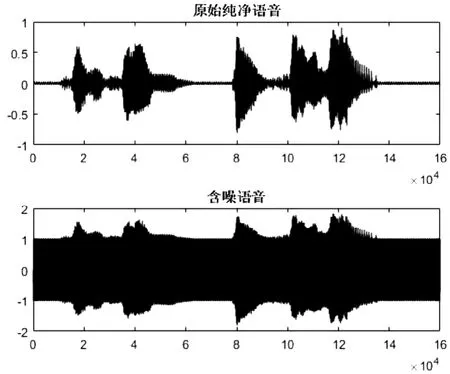
图5 原始信号与含噪信号Fig.5 Original signal and noisy signal

从波形图上看,两种方法都能很好的滤除噪声,从播放的声音效果上,可以听到去噪效果基本相同。通过具体的实例,验证了卷积运算可以实现滤波的效果,所以频域滤波可以通过时域卷积来实现,也验证了卷积定理的内容。

3 结语

通过上述的例子,我们能够更清晰的了解卷积的意义与计算过程,并体会到卷积运算在实际工作和生活中的具体应用,为学好后续知识打下坚实的基础,同时应用M A T L A B 软件编程实现对信号的处理过程,也锻炼了学生的编程能力,调动了学习的积极性,提高了学习效率。

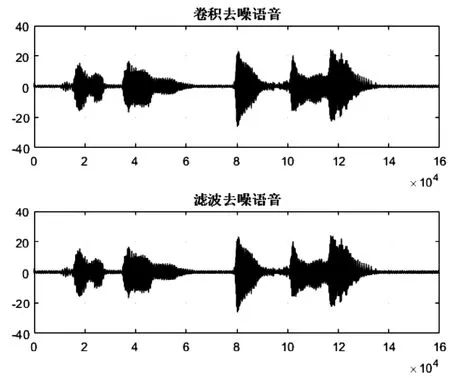
图6 两种方法去噪后的信号Fig.6 Signal denoised by two methods