针对高维数据的马尔科夫毯特征选择

李静星，杨有龙

西安电子科技大学 数学与统计学院，西安 710126

在生物信息学[1]、基因组学[2]、图像处理和文本分类等许多机器学习应用中[3]，越来越多的具有成千上万个特征的高维数据集成为普遍存在的事实[4]。高维数据集中的不相关和冗余特征会导致较高的计算复杂度[5]，严重降低分类精度。同时，高维数据集可能会导致“维数灾难”[6]。因此，处理实际问题中产生的大量高维数据集是一个重大的挑战。为解决这个问题，更好地提取高维数据中有效信息的主要方法是特征选择（Feature Selection，FS）。FS 通过某一准则从原始特征集中选出部分子集组成最优特征子集，然后再应用机器学习算法对数据进行分类分析。其目的是在不造成大量信息丢失的情况下，尽可能多地识别和删除不相关和冗余特征[7]。

传统的特征选择算法是基于信息衡量的单变量特征选择方法，一般是通过信息增益、信息增益率[8]、对称不确定性[9]等信息度量准则计算特征与类属性之间的相关性权值，然后对其进行排序，根据用户定义或给定的阈值选择前K个特征[10]。但是这里K的取值是很难确定的，并且这个方法不能排除冗余特征。近几年，经过国内外学者的研究表明，从本质上来讲，特征选择方法就是一个搜索最优子集的优化问题[11-12]。针对高维数据集的研究，改进后的特征选择算法分为两大部分，首先对原始特征集进行相关冗余分析，然后对输出的子集进行搜索评价得到最优特征子集，其流程图如图1所示。

对于特征选择算法中相关冗余性处理，目前也有一些相应的解决方法。Tsamardinos 和Aliferis[13]将忠实贝叶斯网络中的马尔科夫毯与特征选择中定义的强相关特征进行关联，然后将特征选择任务转移到忠实贝叶斯网络的马尔科夫毯发现问题中。一些学者提出基于马尔科夫毯的滤波器算法，如IAMB[14]、MMMB[15]、HITON_MB[16]、PCMB[17]。这四种方法是在假设数据满足忠实分布的情况下发现单一的马尔科夫毯。但是当数据集不满足忠实分布时，目标节点的马尔科夫毯不唯一，会随着数据集维数的增加呈指数型增加，并且由于特征间的概率关系不易描述，从而导致寻找目标节点的马尔科夫毯具有挑战性。

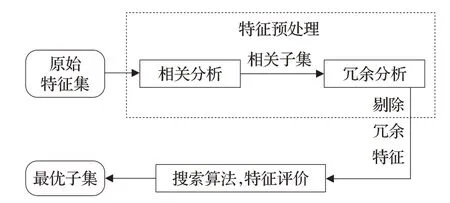
图1 改进的特征选择方法

Statnikov等人[18]提出可以在非忠实条件下发现分布中所有马尔科夫边界的算法TIE*（Target Information Equivalence）。Sun 等人[19]提出了基于近似马尔科夫毯进行特征选择的MIMIC_FS算法，并将得到的子集直接用于训练模型。Yu 等人提出了SRS[20]和SGAI[21]算法，SRS（Selection via Representative Sets）算法对非忠实数据分布进行处理，提出了使用标准的稀疏组lasso从典型集合中选择特征。SGAI（Selection via Group Alpha-Investing）算法首先得到类属性父子节点集中每个特征的代表集，然后通过两种衡量标准分别度量代表集中连续变量和离散变量与类属性的相关性，最后基于衡量标准从权值最高的代表集中选取特征，根据其是否满足惩罚函数判断是否可以加入到预测模型中。在这个过程中没有考虑到冗余特征，并且可能会选到高相关但是低预测的特征。如图2 显示的是数据集Wdbc 在NB 分类器下的分类预测精度随着特征个数的变化情况（特征出现的顺序根据与类属性相关度高低排序），可以看到随着特征子集个数的增加预测能力可能会降低也可能会增加，如何通过搜索算法一次性选出预测能力较高的特征子集显得尤为重要。

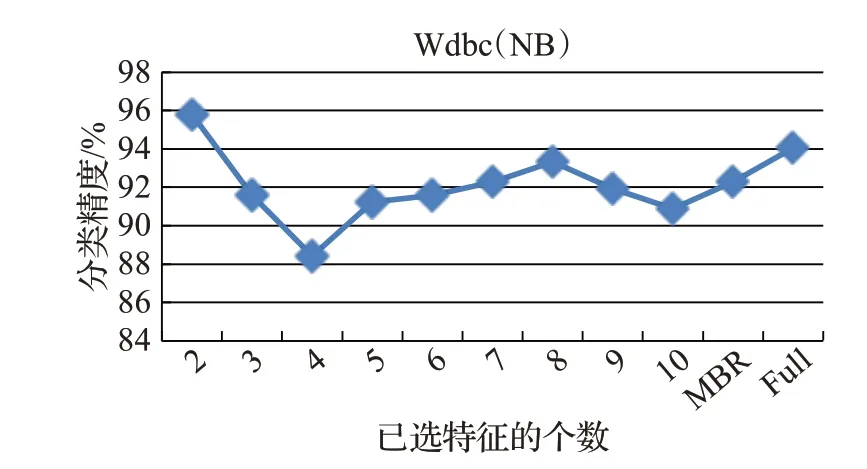
图2 数据集Wdbc的分类精度

为了解决以上问题，本文提出了一种MBRPSO（Markov Blanket Representative Set via Particle Swarm Optimization）的特征选择算法来解决不满足忠实条件的数据分类问题，它充分考虑了特征之间的相关性和特征与子集之间的冗余性，同时又引入了结合特征与类属性相关性和特征子集对分类预测能力的适应度函数，对粒子群算法初始化的粒子进行评价更新。MBRPSO 算法首先利用最大信息系数衡量特征与类属性之间的相关性，得到类属性的马尔科夫毯代表集，然后通过建立特征与子集的冗余性度量准则，删除非主导特征得到次最优特征子集，最后提出新的适应度函数基于粒子群算法选出最优特征子集。通过与先进的特征选择算法和经典的马尔科夫毯滤波器方法比较，在12 个基准数据集上的实验结果表明，MBRPSO 算法对于不同的数据集具有较好的分类效果。

1 特征选择算法MBRPSO

1.1 基础知识

定义1（贝叶斯网络）[22]设G=(V,E)是一个有向非循环图，定义P为随机变量（节点集）V上的联合概率分布，(G,P) 满足马尔科夫条件，因此称B=(G,P)=(V,E,P)为贝叶斯网络。

在有向非循环图G上的分布P隐含着变量间的独立关系。对于三个互不相交的子集X,Y,Z⊂V，如果IP(X⊥Y|Z)成立，则分布P暗含给定Z时X和Y独立，然而从图形的角度看，d-分割也决定着X,Y,Z⊂V间的条件独立关系，可以表示为IG(X⊥Y|Z)。

定义2（忠实分布）[22]如果对于任意三个不相交子集X,Y,Z⊂V满足IP(X⊥Y|Z)⇒IG(X⊥Y|Z)，则称P是定义在G上的忠实分布，记为P∈Faithful(G)。

定义3（马尔科夫毯）[22]设P是变量集V上的分布，变量X∈V，称使得IP(X⊥V-MB-{ }X|MB)成立的一个变量子集MB为X的一个马尔科夫毯。

由以上定义得，如果马尔科夫分布P是G上的忠实分布，则由概率关系决定的条件独立完全等价于图形决定的d-分割。但是当一个数据集不满足忠实分布时，根据定义2的逆否命题，用概率关系推导图中节点的独立是不唯一的，所以此时目标节点的马尔科夫毯不唯一。再者从定义3可得，给定目标节点X的马尔科夫毯MB，则有X与剩余节点独立，即MB中包含了其余特征提供给X的所有相关信息。将这个理念应用到高维数据中，即如果可以找到类属性C的马尔科夫毯MB(C)，则表示不被包含在MB(C)中的特征与类属性C独立，不提供信息，可以安全地删除，因此MB(C)可用于高维数据的特征选择。

利用马尔科夫毯定义高维数据中的冗余特征为：若一个特征Fi是冗余特征当且仅当在特征集F中存在的马尔科夫毯MBi。

1.2 特征预处理

1.2.1 特征相关分析

在之前提出的方法中，信息测量被认为是衡量特征与类属性之间相关性最有效的度量方法之一[23]，通过它可以捕捉特征与类属性之间的线性和非线性关系。为了探索变量间的更多相关性，Reshef 等人[24]提出了一种统计方法，叫做最大信息系数（Maximal Information Coefficient，MIC）。MIC通过蒙特卡罗的思想解决了连续随机变量概率的求解问题，是检测大数据集中各种变量关联的有效手段。最大信息系数主要是通过互信息和网格划分计算得到，将连续随机变量离散在二维空间中并且使用散点图表示，然后用小方格来划分并计算落入每个小方格的概率。其具体实现过程如下：

假设数据集D={(xi,yj),i=1,2,…,n} ，则有随机变量X={xi,i=1,2,…,n}和Y={yj,j=1,2,…,n}，给定划分G，将变量组成的散点图划分为i行j列的网格。根据公式：

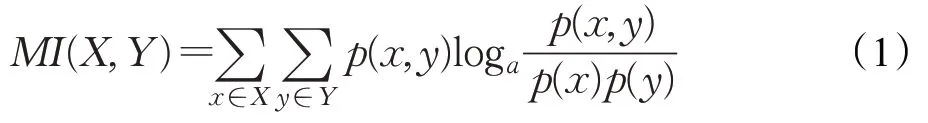
计算每个网格分区的互信息值，并将最大互信息值作为划分G下D的最大互信息，其计算公式为：

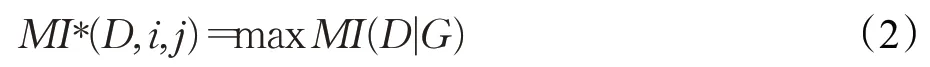
其中，p(x,y)为X和Y的联合概率密度，p(x)和p(y)分别为X和Y的边缘概率密度，D|G表示用G划分数据D。同时将其归一化处理为：

由于G有多种形式，将取不同划分方法下的最大互信息值作为最大信息系数值，定义为：

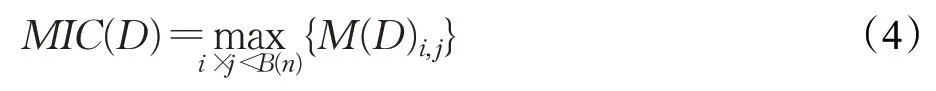
其中，B(n)为i×j网格的上限，一般取B(n)=n0.6，n为数据的大小。

MIC不仅可以应用于离散数据和连续数据，也可以度量线性和非线性变量之间的关系，挖掘出变量间的函数依赖关系。本文将MIC 应用到马尔科夫毯中处理特征间的相关性问题。由于目标节点的马尔科夫毯由目标节点的父子节点PC和配偶节点组成，但是配偶节点寻找的概率模型不易描述。因此，可以转化思想，寻找类属性父子节点的父子节点，从而构成类属性的马尔科夫毯代表集，解决不忠实条件下马尔科夫毯不唯一的问题。

从概率角度来看，如果：

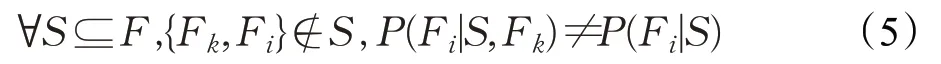
则Fk称为Fi的相关特征。记作Fk=Cor(Fi)。在贝叶斯网络中，如果在Fi∈F和Fk∈F之间存在有向边，那么称Fk和Fi直接相关。

在本文中利用MIC 衡量特征与类属性之间的相关性，然后将得到的权值排序取相关度高的特征子集组成类属性的父子节点ξ=PC(C)，令Rs1,Rs2,…,Rsk为ξ=PC(C)中每一个特征的代表集，定义Rsi={Fi⋃Cor(Fi)},Fi∈ξ,i=1,2,…,k，令

为类属性的马尔科夫毯代表集。

如果一个特征Fi在当前的特征集中存在一个马尔科夫毯Mi，则表示Mi包含了Fi对类属性C和其他特征F-Mi-{Fi}的所有相关信息，因此可以安全地删除Fi。通过对特征与类属性之间的相关性分析，得到类属性的马尔科夫毯代表集，从而可以排除其他特征减少特征搜索空间。

1.2.2 特征冗余分析

由前面讨论可知，在寻找类属性马尔科夫毯代表集的过程中，会含有一些冗余特征被选择，所以需要建立冗余性衡量准则剔除代表集中的冗余特征。

给出一个已被选择的特征子集S={Fi}⊆F，以及一个任意的特征Fi∈F⋂Fi∈S，定义特征Fi与子集S的相关性为：

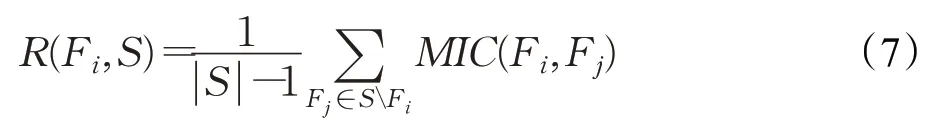
当且仅当特征与类属性的相关性较低且与马尔科夫毯代表集相关性较高时，特征被称为非主导特征。

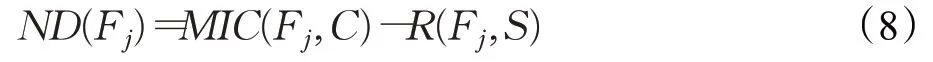
即当等式（8）的值较小时，称Fj为非主导特征。找出这类特征，将其从马尔科夫毯代表集中删除得到次最优特征子集。例如，图3表示类属性C的次最优特征子集寻找过程，图中的几个蓝色节点表示类属性的父子节点，用红线标出的几个大圈表示类属性的马尔科夫毯代表集。即蓝色节点的父子节点组成的集合，假设节点K的ND(K)值较小，小于给定的阈值θ时，剔除节点K，则得到的集合就是类属性的次最优特征子集。

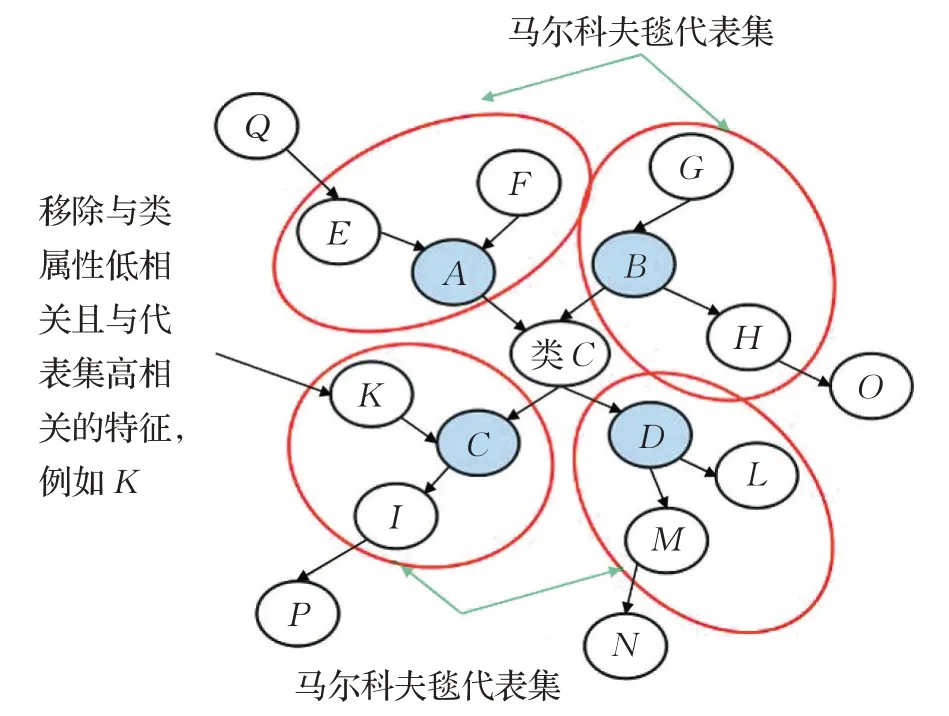
图3 类属性C 的次最优特征子集

1.3 选出最优特征子集

1.3.1 适应度函数的提出

在对数据集的原始特征集进行特征预处理得到类属性的次最优特征子集之后，采用粒子群算法寻找最优解。通过提出相应的适应度函数来确定粒子的最佳位置，从而通过迭代对粒子进行更新，找到问题的最优解，其关键一步就是建立适应度函数。本文利用加权系数μ将平衡分类精度与相关性度量结合得到新的适应度函数，公式如下：

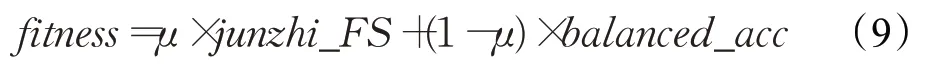
其中，balanced_acc表示平衡分类精度，计算公式为：

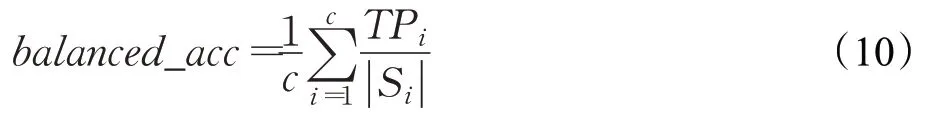
c为类别个数，TPi为第i类正确识别的实例数，为第i类的样本量，所有类均以的权重进行处理。

式（9）中的junzhi_FS表示使用逻辑损失函数将junzhi_MIC归一化得到的值，junzhi_MIC表示当前特征子集与类属性C的最大信息系数均值，其具体计算过程如（11）、（12）所示：

nOfselection是当前选进最优特征子集中的特征个数，MIC(Fk,C)表示当前子集中的特征与类属性的最大信息系数值。逻辑损失函数的参数选择见图4（b），采用系数为-6 的逻辑损失函数可以将均值归一化到[0.5，1]，系数为-1 的逻辑损失函数如图4（a）所示，不能将输入的均值返回到全范围的[0.5，1]中。

1.3.2 MBRPSO算法的实现

本文使用粒子群算法搜索评价特征子集。首先随机产生一群初始化粒子，每个粒子的位置代表一个完整的候选解决方案，粒子实际上是一个有N维实向量，其中N是设定的最优子集特征个数。通过位置和速度两个参数来描述一个粒子的运动状态。并且在每一次迭代中，通过适应度函数记录每个粒子的个体历史最优位置和群体的历史最优位置，最后利用这两个最优位置再结合粒子本身的惯性共同影响粒子的运动状态，由此来更新粒子的位置和的速度。在这个算法中粒子仅有两个属性：速度和位置，速度代表移动的快慢，位置代表移动的方向。位置速度和位置更新是粒子群算法的核心，其原理表达式和更新方式如下：

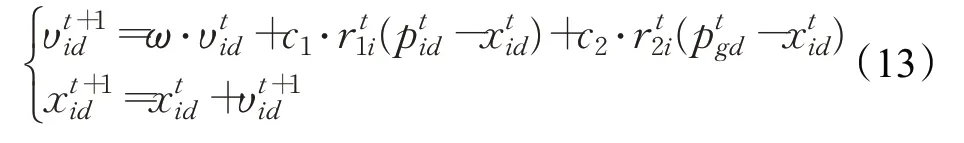
图4 逻辑函数参数的选择

算法1MBRPSO算法

输入：训练集T，特征集合F=(F1,F2,…,Fn,C)，阈值θ和权值系数μ。

输出：最优特征子集FS。

1.fori=1,2,…,n//特征集合中任取一个特征

计算每个特征与类属性的最大信息系数值MIC(Fi,C)；end

2.将MIC(Fi,C)值从大到小排列，得到贝叶斯网络中与类属性C相关的父子节点ξ=PC(C)

3.记K=| |ξ//ξ中特征的个数

4.forj=1,2,…,K//特征集ξ中任取一个特征Rsj=PC(Fj)⋃Fj,Fj∈ξend

5.获得类属性C的马尔科夫毯代表集，记Rs=|L|；

6.当Rs≠Null 时

7.fork=1,2,…,L//从代表集中任取一个特征

8.如果

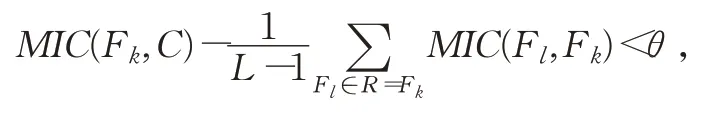
则从Rs中剔除特征Fk

9.否则，继续上述操作

10.end

11.返回类属性的次最优特征子集S；

12.初始化粒子

13.使用式（9）计算每个粒子的适应度函数值，更新粒子的位置和速度，得到最优特征子集FS返回一个具有特定个数的最优特征子集。

2 实验及结果分析

主要评估所提出的MBRPSO 算法的有效性。将MBRPSO 算法与四种先进的特征选择方法和四种经典的马尔科夫毯滤波器进行比较，分别使用三种分类器对来自不同研究领域并且有着不同规模的12个数据集进行实验分析比较，从而验证MBRPSO 算法的可行性和有效性。

2.1 数据集

在表1中，选择了UCI的12个基准数据集，其中有5个机器学习数据集存储库（Spect、Wdbc、Spectf、Promoter、Spambase）、4 个生物医学数据集（Colonoscopy、Scadi、Arrhythmia、Dermatology）、2 个 2003NIPS 特征选择挑战数据集（Madelon、arcene）和1 个图像处理数据集（DrivFace）。这12个数据集涵盖了广泛的实际应用，包括临床成像、基因表达、生态学和分子生物学。12个数据集的维度从22到10 000、样本大小从70到数千、数据集的类别从2到16，代表性广泛。对表1中的每个数据集，随机选取50%的实例作为所有实验应用的训练数据集，其余50%的实例作为测试数据集。利用训练数据通过各种特征选择方法来选择最优的特征子集。然后将所选择的最优特征子集应用于测试数据。

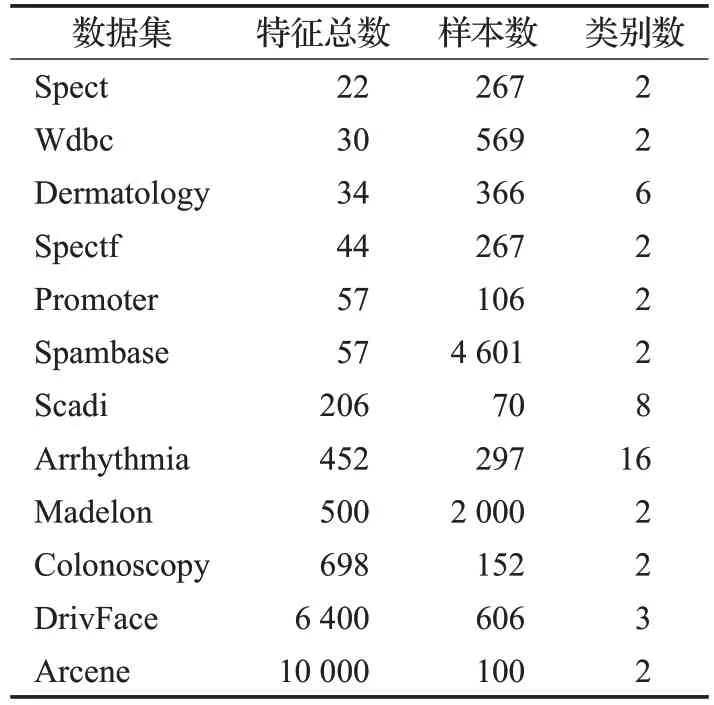
表1 实验数据集

2.2 实验装置

对于表1 中的每个数据集，使用了三个分类器，分别是MATLAB 统计工具箱提供的NB 和KNN 分类器，LIBSVM库提供的SVM分类器，分析数据的预测误差，从而评估特征选择算法的有效性。为了避免所选数据的偏倚，使实验更有说服力，使用十折交叉验证对特征子集进行测试和评价，重复实验20 次。本文将提出的算法与四种经典的马尔科夫毯滤波器和四种先进的特征选择方法进行比较分析。

对于先进的特征选择方法，主要采用以下四种方法进行比较：（1）TIE*算法[18]，在数据集不满足忠实条件时，以HITON_PC作为基本寻找所有的马尔科夫毯，其中参数的设置详见文献[18]。（2）MIMIC_FS 算法[19]，基于最大信息系数和近似马尔科夫毯对特征进行选择，关于参数的设置见文献[19]。（3）SRS 算法[20]，在不忠实的情况下，提出了利用稀疏组从典型集合中选择特征子集，其参数的具体设置见文献[20]。（4）SGAI算法[21]，基于对称不确定性和概率密度函数建立代表集与类属性之间的相关性权值，然后根据权值从每个代表集中选择特征组成最优子集，其关于搜索算法的参数设置见文献[21]。除去这四种特征选择方法，本文还将MBRPSO 算法与1.2节提出的马尔科夫毯代表集Rs进行比较。

对于经典的马尔科夫毯滤波器，主要采用以下四种方法进行比较分析：（1）IAMB[14]，在忠实性的假设下采用启发式搜索从高维数据库中学习类属性的马尔科夫毯。（2）MMMB[15]，采用分治法分两步搜索目标节点的马尔科夫毯。（3）HITON_MB算法[16]，旨在缓解IAMB算法中数据效率低下的问题，同样是分两步学习马尔科夫毯。（4）PCMB 算法[17]，不需要学习全都的贝叶斯网络，而且识别目标节点的马尔科夫毯所需的实例个数不取决于马尔科夫毯，克服了数据无效率的问题。四种算法的显著性水平取为0.01。

在本文提出的MBRPSO 算法中，阈值θ用于控制单个特征与特征子集的冗余性。每个数据集的阈值不一样，取决于每个特征与已选子集的最大信息系数值。对于表1 给出的数据集，θ的取值范围为[-0.3,0.1]。粒子群算法中的惯性权重ω取为0.2，学习因子c1,c2取为2。适应度函数中的参数μ取值为[0.2，03]，迭代次数为50，初始化粒子的大小为特征数20（限制最大为300）。

2.3 实验结果分析

特征选择的目的是在特征信息较少遗漏的情况下，选择较少的特征达到较高的分类预测能力。因此，本文通过分类预测能力和算法最终选择的特征个数两方面对算法的有效性进行分析评价。

2.3.1 比较MBRPSO与先进特征选择算法

（1）比较分类预测能力

表2、表3和表4显示了MBRPSO与SGAI、MIMIC_FS、SRS、Rs、TIE*的实验结果，以及展现了使用不同分类器的同一种特征选择方法在不同数据集下的平均分类精度，最低的预测误差以粗体突出显示。从表中可以看出，MBRPSO 算法的分类性能优于其他先进的特征选择方法。由于所选数据分为离散数据和连续数据，以及两类数据和多类数据，这些都会对数据集的分类和预测能力产生影响。对于KNN分类器，在本节的12组实验中，MBRPSO算法在10个数据集中始终优于其他方法，其平均值为84.77%，分别比SGAI、MIMIC_FS、SRS、Rs和TIE*高出6.23%、3.84%、7.03%、7.96%和6.57%。对于NB 分类器，MBRPSO 算法在8 个数据集中始终优于其他方法，其平均值为85.53%，分别比SGAI、MIMIC_FS、SRS、Rs和TIE*分别高出7.09%、9.65%、7.60%、7.61%和4.13%。对于SVM分类器，MBRPSO算法在9个数据集中始终优于其他方法，平均为85.49%，分别高出其他算法6.28%、7.42%、7.25%、6.72%和5.52%。

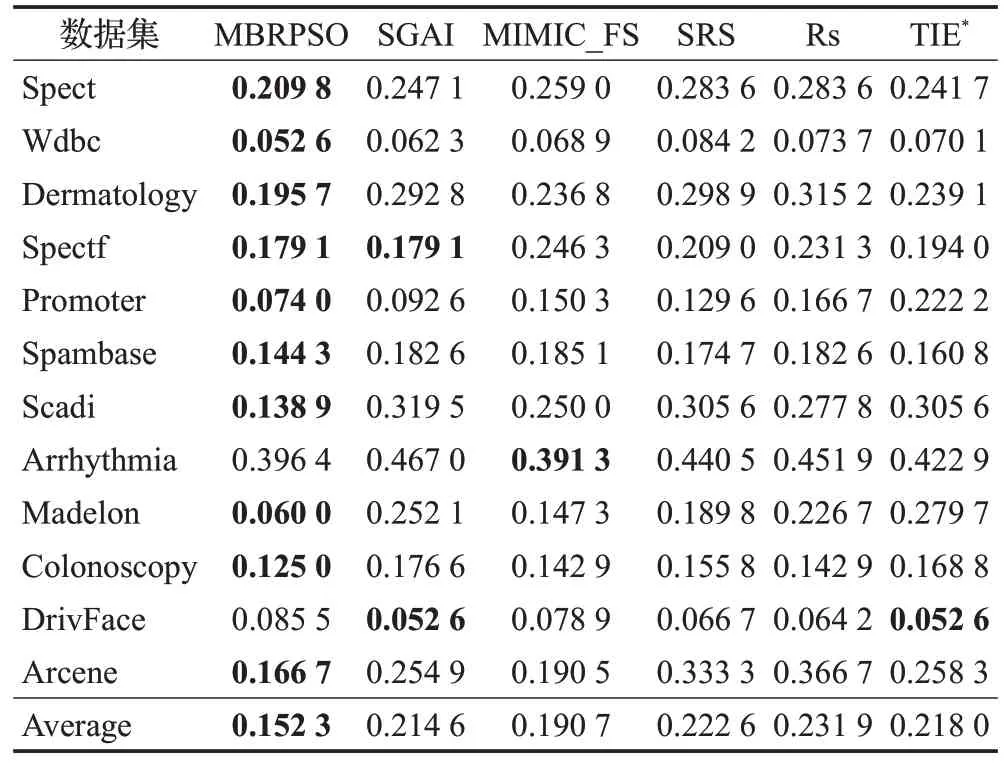
表2 五种特征选择在KNN上的平均分类精度比较

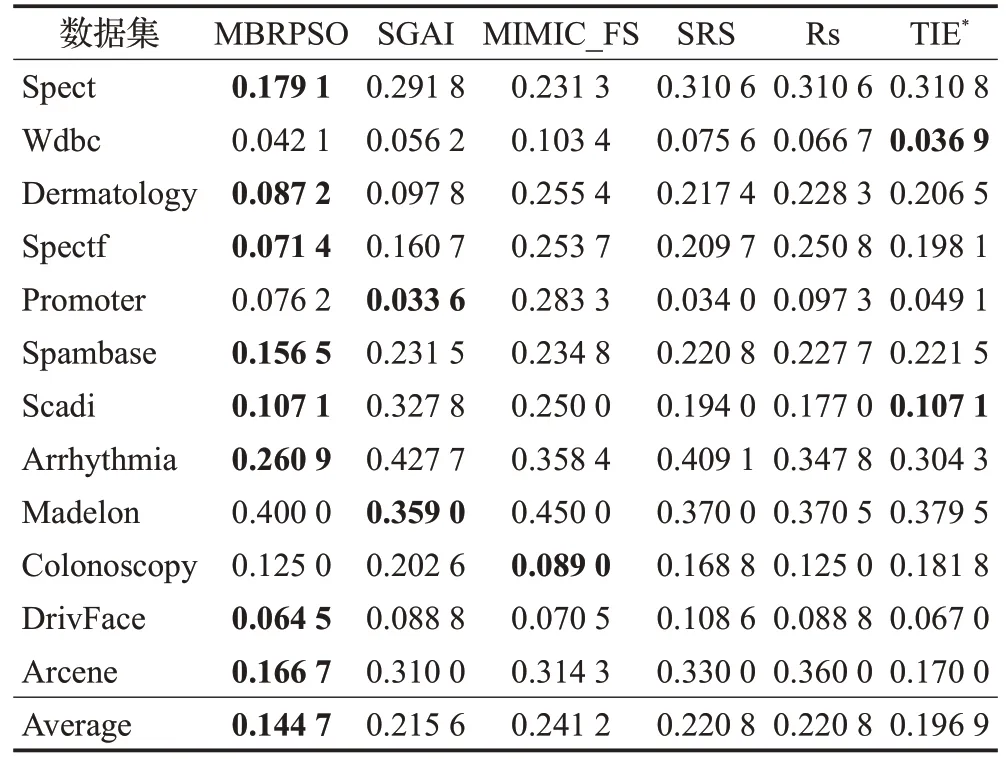
表3 五种特征选择在NB上的平均分类精度比较

以上比较中，MBRPSO 与SGAI 都是通过衡量特征与类属性的相关性，然后通过高相关的特征组成代表集，进而利用搜索算法选出最优子集。主要不同之处在于MBRPSO 得到的是类属性的马尔科夫毯代表集，并利用搜索算法选出一组特征。而SGAI得到的是每个高相关特征的代表集，从空集出发，在每个代表集中一个一个选出特征。通过这两个算法的比较可以直观地看出一次性选出特征子集的优势。其堆积百分比柱状图如图5 所示。图中主要体现的是不同的特征选择方法利用不同分类器的预测误差比较，可以看出特征选择方法与何种分类器搭配预测能力最大。在KNN中，8组准确率差异均在3%以上，分类准确率最高的为19.21%。MBRPSO 中最差的实验结果比SGAI 低3.29%，算法性能具有可比性。通过分析SVM 和NB 分类器的实验结果，得到了MBRPSO 算法的分类性能优于SGAI 算法。从图中看出，与SGAI 相比，MBRPSO 对于多类数据集具有更高的分类预测精度，当样本数量远远大于特征数量时，MBRPSO的效果略差。

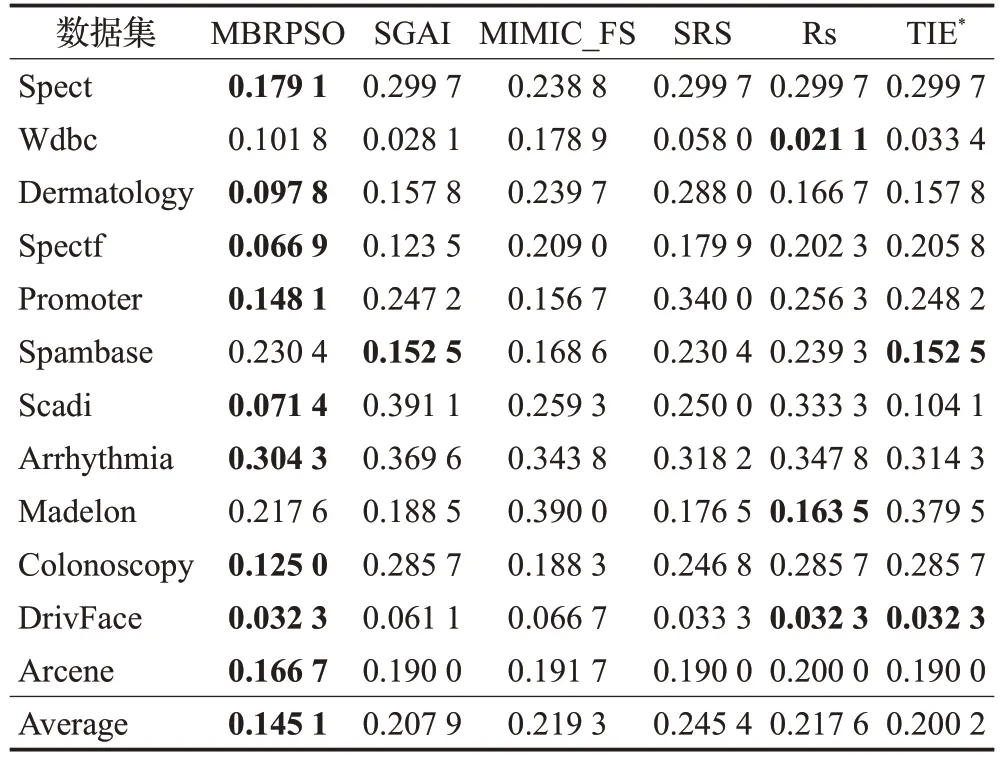
表4 五种特征选择在SVM上的平均分类精度比较

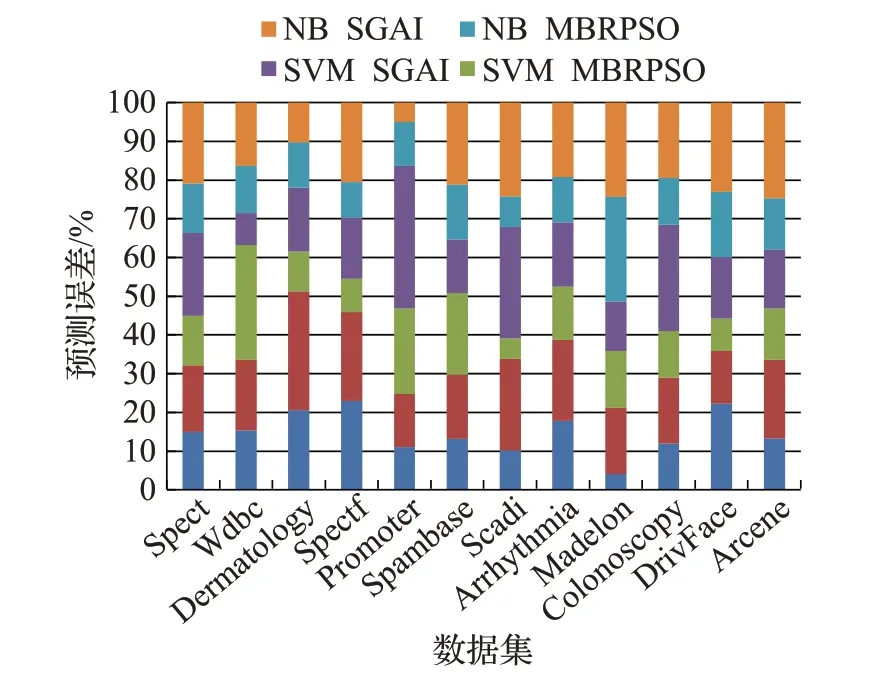
图5 MBRPSO与SGAI基于三种分类器预测误差的比较

（2）比较最终选择的特征个数

图6（a）～（e）显示了使用 SGAI、MIMIC_FS、TIE*、SRS 和Rs 选出的特征数与MBRPSO 算法的比较结果。表5为MBRPSO算法最终选出的特征数。在大多数数据集中，MBRPSO 算法选择的特征比其他算法少。MBRPSO 从特征与类属性的相关性角度出发，最大限度地保留了与类相关的、更有区别性的特征。在特征之间的冗余方面，MBRPSO 可以更有效地去除冗余特征，进一步减少特征之间的冗余，从而在特征分类数据较少的情况下达到最高的分类性能。重要的是，MBRPSO 可以预先确定最终选择特征子集的数量。其他先进的马尔科夫毯特征选择算法在特征数量方面具有不确定性和不灵活性。

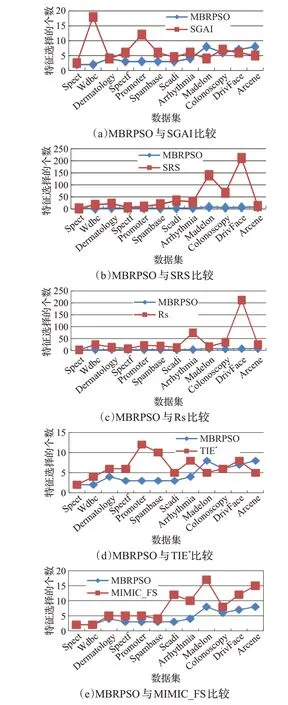
图6 算法所选特征个数的比较

表5 MBRPSO选出的特征数量

2.3.2 比较MBRPSO与马尔科夫滤波器

（1）比较分类预测能力

表6～8 分别给出了算法MBRPSO、IAMB、PCMB、HITON_MB和MMMB的预测误差，以及同一特征选择方法在不同数据集中的平均分类精度。最低的预测误差以粗体突显。从表中可以看出，MBRPSO 的分类性能优于其他马尔科夫毯滤波器，体现出在数据集不满足忠实分布的情况下，引入马尔科夫毯代表集的优势。分析表6得对于KNN，在本节的12组实验中，MBRPSO算法在9 个数据集中始终优于其他方法，其平均值为84.77%，分别比IAMB、PCMB、HITOM_MB 和MMMB高4.28%、7.69%、3.48%和6.97%。表7展现出了对于NB，MBRPSO 算法在10 个数据集中始终优于其他方法，其平均值为85.53%，分别比IAMB、PCMB、HITOM_MB和MMMB高9.44%、10.07%、5.43%和7.78%。从表8可得，对于SVM，MBRPSO算法在9个数据集中始终优于其他方法，其平均值为85.49%，分别比IAMB、PCMB、HITOM_MB和MMMB高9.16%、8.97%、7.09%和7.94%。

表6 五种特征选择过滤器在KNN上的平均分类精度比较

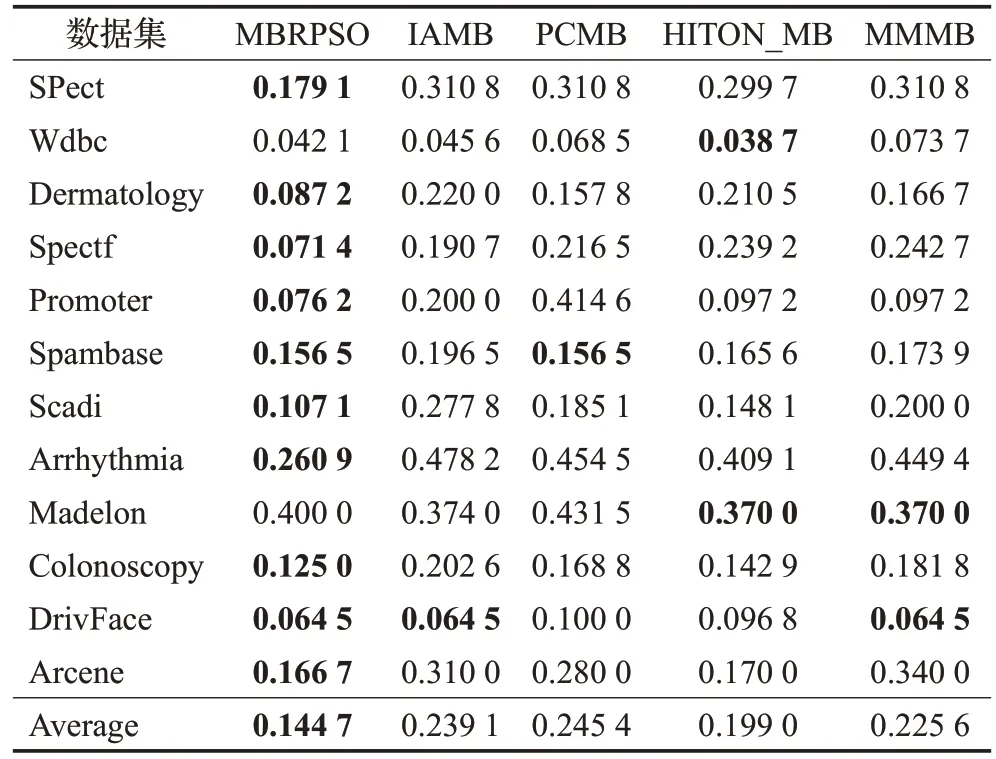
表7 五种特征选择过滤器在NB上的平均分类精度比较

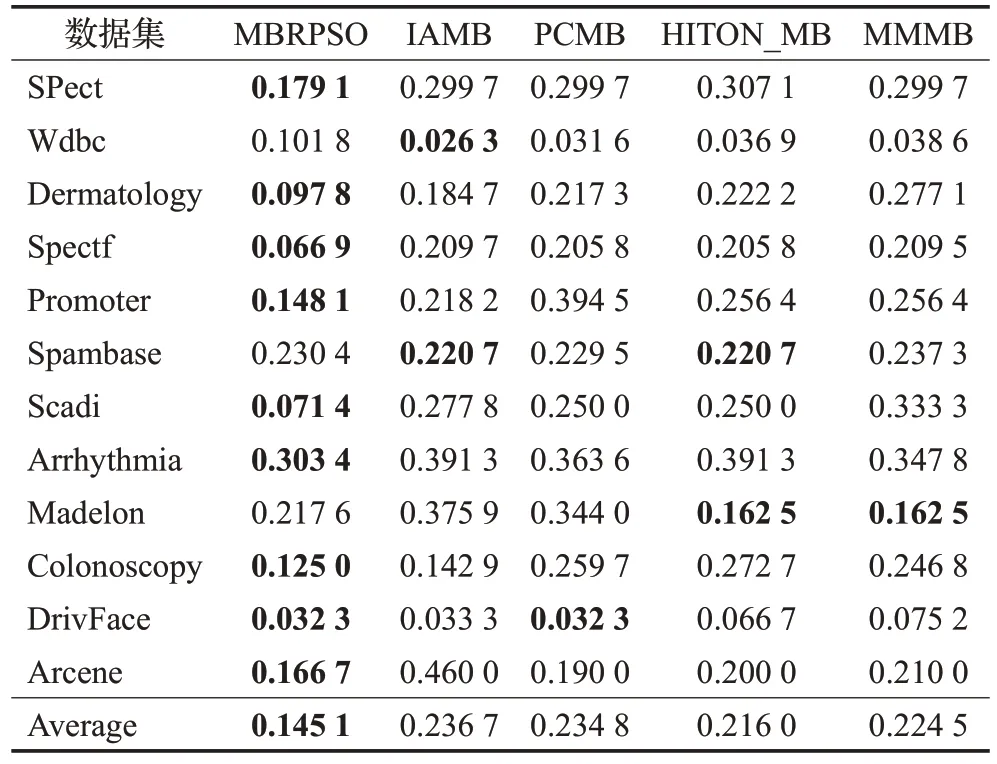
表8 五种特征选择过滤器在SVM上的平均分类精度比较

（2）比较最终选择的特征个数

从图7 显示了MBRPSO 算法选出的特征数与其他算法特征数的比较。分析得到这五种算法在9 个数据集上选出的特征数是相近的，并且在剩余的数据集中，MBRPSO算法与IAMB和HITON_MB算法选出特征数相差较大，与MMMB 和PCMB 算法选出的特征数相近。在特征个数相近的数据集中，可以由分类预测误差得到，MBRPSO算法的性能更强。

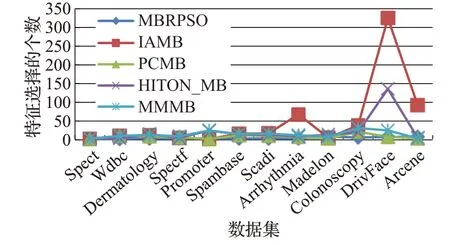
图7 五种算法特征个数的比较

综上所述，研究表明：在数据集不满足忠实条件的情况下，单一的马尔科夫毯特征选择算法选出的特征并不是有较高预测能力的最优特征集。而MBRPSO不需要对真实数据集中所有马尔可夫毯的未知空间进行彻底的搜索，就可以通过剔除与类属性和代表集冗余的特征，有效地找到特征选择的最优特征子集。

3 结束语

随着社会信息化的迅猛发展，数据规模的巨大化，数据结构的复杂化以及数据表现形式的多样化，使得从数据集中提取有效的信息，处理高维数据的分类问题变得极其困难。所以利用特征选择方法避免维数灾难减小特征搜索空间变得尤为重要。

本文针对高维数据的特征选择问题，提出了一种有效的算法MBRPSO来解决数据集不满足忠实分布时类属性的马尔科夫毯发现问题。MBRPSO 算法主要通过最大信息系数建立特征与类属性相关性和特征与子集冗余性的衡量准则，从而得到类属性的马尔科夫毯代表集和次最优特征子集对原始特征集进行预处理，然后设立同时考虑特征子集的相关性和预测能力的适应度函数，利用粒子群算法选出最优特征子集。实验结果表明，与其他相关方法相比，采用特征预处理步骤缩小原始特征集的搜索空间并基于集合的形式搜索最优子集，可以在测试阶段提高分类精度且起到显著的降维效果。