结合马田系统-SVM的滚动轴承故障模式分类研究

韩卫宇，程龙生

南京理工大学 经济管理学院，南京 210094

当前随着互联网、物联网、5G无线通信、移动终端、智能传感器技术的发展和成熟，催生了工业互联网的诞生。工业互联网的本质是将人、机器、数据有机地相连接[1]。机械设备的故障模式分类是工业互联网重要的应用场景之一。在机械设备的关键部件中，滚动轴承是最通用的，最重要的也是最容易发生故障的。在对机械设备的故障产生原因进行统计分析后，发现有将近30%的故障是由滚动轴承的退化而导致的[2]，因此对滚动轴承进行故障模式分类是有意义的，对于日常修理或者更换工作提供了决策依据，既降低了维护成本，又提高设备的可靠性，保证设备正常运行。

在基于振动信号特征提取的滚动轴承故障模式分类中，第一步也是最为关键的步骤就是提取振动信号中有效的故障特征，其将直接影响到整个模型的准确率和效率。采集轴承振动信号的传感器所处的现场环境嘈杂，导致信号中含有大量干扰噪声。并且处于故障状态的振动信号本身就具有非平稳、非线性的特性[3]。常用的信号处理方法包括短时傅里叶变换、小波变换和基于Hilbert-Huang变换（HHT变换）。HHT变换又包括经验模态分解（EMD）和希尔伯特变换。短时傅里叶变换和小波变换等方法无法自适应地根据数据本身特性做相应处理，具有一定的局限性。而EMD 是一种新型自适应信号时频处理方法，于1998 年由Huang 提出来的[4]。EMD 方法在理论上能够分解任何类型的信号，在处理非平稳及非线性数据上，具有非常明显的优势。Ali[5]用EMD提取特征向量，然后利用神经网络进行模式识别，实现了轴承故障模式分类。Guo等[6]采用基于多目标优化的EMD 方法提取滚动轴承故障特征，用于故障识别与分类。但是EMD 分解存在模态混叠现象，影响分类的准确度。为了解决该问题，Huang 等[7]于2009 年提出了一种人为添加白噪声的方法进行信号处理—集合经验模态分解（Ensemble Empirical Mode Decomposition，EEMD），该方法是在原始信号中加入了高斯白噪声，然后再进行多次EMD分解。Deng等[8]结合EEMD和相关系数法计算出轴承的故障特征用于故障模式分类，所提的特征提取方法可以有效地消除模态混叠的影响。Yu 等[9]利用EEMD 和SVD（奇异值分解）从轴承的实时状态数据中提取有效的故障特征，用于状态评估。胡谧[10]先通过变换对信号进行降噪，然后利用EEMD 和HHT变换得到信号的边际谱进行故障识别。

马田系统是一种理论基础深厚，应用场景广泛的多元统计方法，包括了特征约简和分类预测两部分。Shakya[11]采用施密特正交化MTS 有效地筛选出振动信号的时域、频域等多个特征，从而对滚动轴承进行了故障诊断。Zhao[12]将拉普拉斯算子用于降低输入MTS的特征维度，从而对滚珠进行健康评估。

常用的用于分类的机器学习算法有人工神经网络（ANN）、决策树（DT）等。但基于ANN的滚动轴承故障模式分类，需要训练大量的样本，学习速度慢，但是滚动轴承的样本数量少，因此训练很可能会失败。而DT 易出现过拟合问题导致泛化能力不强，也容易忽略各个指标属性之间的相关性等问题。SVM表现出相较于其他算法的优势主要体现在SVM的理论基础是统计学习理论，遵循结构风险最小化原则，具有小样本学习能力，即使训练样本数量较少也只会产生微小误差。并且对独立的测试集仍能保证小的误差，泛化能力强。同时SVM的模型复杂程度与特征空间的特征数量无关。由于SVM 的分类决策函数是由少数的支持向量（Support Vector）确定，其模型的复杂度和计算量只和支持向量的个数有关，不会发生所谓的“维数灾难”。

随着SVM 理论的不断完善，学者也将其运用的不同实际领域中进行模式识别。在滚动轴承故障模式分类中，Zhang[13]等通过EEMD对振动信号进行分解，从中提取了信号的奇异值和能量熵指标，然后使用SVM 对轴承的故障类型进行分类。秦波等[14]提出了一种基于小波包、奇异值分解和GA-SVM 的轴承故障诊断方法。SVM 参数C和δ对分类精度的影响很大，但是难以提前确定合适的取值。各位学者纷纷引入优化算法帮助寻优，如网格搜索算法、蚁群算法、遗传算法等。但这些算法在优化参数时存在一些劣势，如计算开销大导致的寻优效率低等问题。相比之下，PSO算法具有诸多优点，如可调参数少、寻优效率高。所以本文通过粒子群算法优化支持向量机。

SVM 最初是解决二元分类问题的，不能直接进行多分类，必须引入多分类算法。刘志刚[15]总结了SVM在多分类推广的方法，从训练速度、测试速度和泛化水平等维度比较了每个算法的优劣势。

综上所述，本文提出结合马田系统和SVM 的故障模式分类方法。使用特征生成法构建初始多维特征空间，然后使用马田系统进行降维，得到精简特征空间，然后输入到SVM多分类模型中进行故障模式分类。实验结果表明，该方法可以有效识别故障的类型并确定受损程度。

1 相关理论基础

1.1 EEMD方法

EEMD分解步骤如下：

（1）多次在原信号里加入幅值系数为k的白噪声序列ni(t)(i|=1,2,…,h),得到h个新信号，如式（1）所示：

（2）对新信号xi(t)进行EMD 分解，分别得到n个IMF分量，记为cij(t)(j=1,2,…,n)，余量记为ri(t)。

（3）计算每个新信号分解后所得到的IMF的均值和RES的均值，把其看做是最后所得到的IMF分量及余量结果，如式（2）所示：

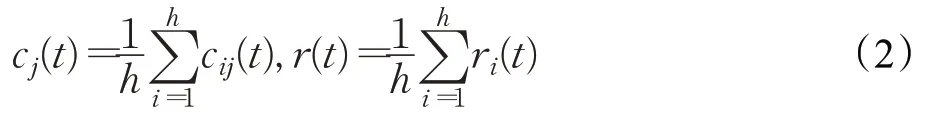
式中，cj(t)表示EEMD分解得到的第j个IMF分量；r(t)表示EEMD分解后的残余函数。

1.2 故障敏感IMF选取方法

在EEMD分解过程中，原始的滚动轴承信号将会成为一系列不同频率范围内的IMF，其中不同的IMF中往往包含了不同的故障信息，也与故障的相关性差别很大，所以对于故障的表达能力存在比较大差异。如果盲目将所有IMF 参与构建初始特征空间，会引入冗余信息，导致运算量增加，识别效率降低，甚至会影响分类准确率。若能有效地建立IMF分量与故障的相关关系，将会为IMF的挑选提供依据，从而挑选出对于故障信息敏感的IMF，去除其他IMF 干扰成分，提高轴承故障特征提取的效率和可靠性。所以在此基础上，本文提出了故障敏感IMF选取方法。该算法具体流程如下：

（1）计算振动信号x(t)和其各IMF分量d1(t),d2(t),…,dn(t)的相关系数pi为：

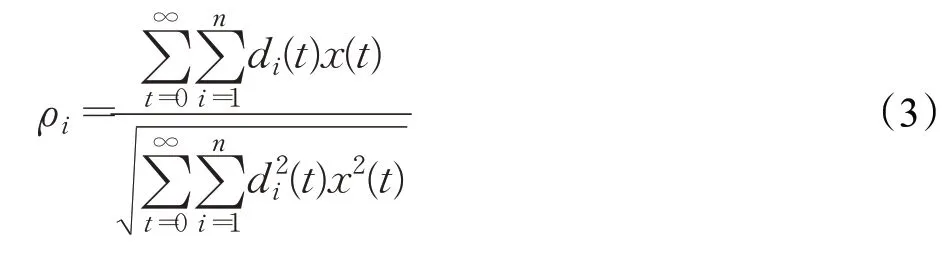
（2）计算各IMF分量的敏感因子：

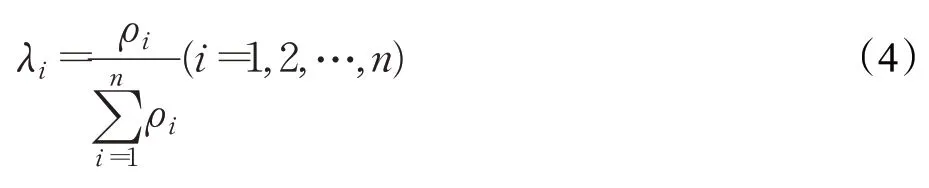
（3）按敏感系数从大到小的顺序将IMF 重新排序，得到新的IMF 序列{d′n(t)} (i=1,2,…,n)，并计算敏感系数的累计和：

（4）给出选择阈值η，当第k个IMF 的敏感系数的累计和hk ＞η，而第k-1 个IMF 的敏感系数的累计和hk-1＜η时，那么 { }d′n中的前k阶 IMF 即为故障敏感的IMF，该算法的阈值η根据具体问题而确定。该算法本质上是根据IMF各分量与原信号的相似性，旨在突出与故障特征相关性大的成分。

1.3 马田系统特征筛选

1.3.1 马田系统原理

马田系统（MTS）是日本著名质量工程学家田口玄一博士提出来的一种针对多变量的模式识别方法。马田系统包括两个部分，即特征变量筛选和样本类型判断。马田系统的核心方法包括了马氏距离、正交表和信噪比等方法。MTS 利用田口方法（包括正交表和信噪比）筛选有效特征变量，剔除冗余变量，从而实现优化空间的工作。

在马田系统中，是根据马氏距离的大小来进行决策归属的，为了避免变量的数量不同影响决策，马氏距离都要除以变量数量，这样在基准空间中的样本数据的马氏距离平均值为1。逆矩阵法是计算马氏距离的常用方法，它的核心是计算相关系数的逆矩阵。设空间F中包含了n×p个样本，n是样本个数，p是样本的变量个数，第i个样本的第j个变量的值为xij(i=1,2,…,n;j=1,2,…,p) ，对空间F进行标准化处理得到tij=(xijxˉj)/sj，xˉj为变量j的均值，sj为变量j的标准差，从而得到样本标准化的向量Ti=(ti1,ti2,…,tip)T,i=1,2,…,n。变量间的相关系数矩阵为U，其逆矩阵为U-1，则第i个样本的马氏距离为：

在多元系统中，数据的变量越多，会增加分类的计算量，降低分类的效率，并且变量与变量之间所表达的信息可能是相同的。所以有必要去除冗余变量。在马田系统中，使用二水平正交表和信噪比来筛选特征变量。

正交表是质量工程学的试验设计的方法，田口玄一将其借鉴过来，目的是通过相对少的试验次数来找到最佳的变量搭配。在MTS 中只使用两水平的正交表，即使用和不使用该变量。在该表中水平“1”指的使用该变量参与建立基准空间，水平“2”与之相反。

信噪比从字面意思来说是指信号与噪声之比，将有效信号与干扰噪声的比值来评价设备的能力，单位为dB。田口玄一将信噪比引入正交实验中的主要目的是作为指标筛选的规则。

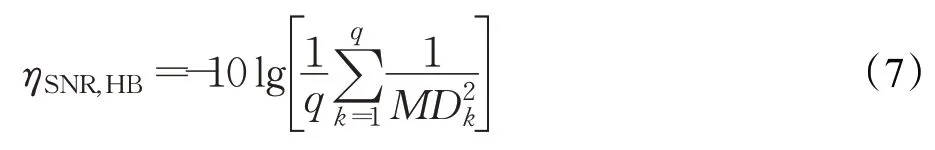
在MTS 中，通过二水平正交表可以构建不同的基准空间，利用每个基准空间计算异常样本的MD，然后根据式（7）计算出每一个试验条件下的信噪比，从而求出每个变量的主效应。

MTS 中特征变量的选择由变量的信息增益差Δ（即变量的主效应）决定。一般来说，信息增益差Δ越大，表明该变量有助于提高分类准确度：

SNR+表示正交表中某个变量水平为“1”时的信噪比之和，SNR-表示正交表中某个变量水平为“2”时的信噪比之和。如果Δ大于0，说明该特征变量对分类起到积极作用，应该挑选该变量；如果Δ小于0，说明该特征变量对分类起到消极作用，应该舍弃该变量。这样就完成了特征变量筛选的工作，使分类效率和准确率更高。

1.3.2 筛选特征变量步骤

马田系统中只有正常样本和异常样本两类数据。根据研究问题的实际情况，定义正常样本并确定原始的特征变量，从而构建基准空间。计算基准空间的均值向量和协方差矩阵等信息。正常情况下，基准空间内正常样本的马氏距离均值大约为1，这种特点使得基准空间可以作为测量尺度的参考集，对识别异常样本有明显的效果。运用2水平正交表Lq(2n)来进行试验，正交表的每一列表示一个变量，每一行表示一次试验。在每一次试验时，都会选择不同的变量组成一个数据集，生成对应的基准空间。在每一次试验过程中，首先先计算正常样本的均值、标准差和协方差矩阵，然后使用正常样本的均值、标准差、协方差矩阵再计算所有异常样品的马氏距离，将结果代入式（7）这样就得到了信噪比。最后计算各变量的信噪比增量，大于0予以保留，小于0予以剔除。这样就得到了最优的变量组合，实现了优化基准空间的目的。

1.4 偏二叉树多分类方法

SVM 是用于解决多维模式识别中的二分类问题。但是，在实践中存在很多多分类问题。因此，构造合理的多分类算法是扩展马田系统应用场景的重要手段。多分类问题可以表述为：给定属于k类的m维n个训练样本 (x1,y1),(x2,y2),…,(xn,yj),其中xi∈Rm,i=1,2,…,n，且yj∈{ }

1,2,…,k，要通过上述训练样本构造一个分类函数f，使对未知样本x进行分类时，错误率尽可能小。目前，一般解决多分类的方法是将多个二分类器相互连接，组成一个整体，当输入样本的数据就输出样本类别。不同的连接方式适用不同的样本，有不同的分类效果。目前多分类器一般包括“一对多”法、“一对一”法、有向无环图法和二叉树法等。二叉树分类器在训练数据时只需建立k-1 个分类器，并且也不需经历所有分类器和所有类别的数据。因为越往下一层级训练，参与训练的数据越少，效率越高。相较于其他三种分类法，它的训练效率、决策速度和预测精度均较高。

虽然二叉树分类器有诸多优点，但是如果待解决的问题背景比较复杂时，二叉树模型层次结构的建立存在一定风险，因为二叉树的不同层次结构对分类精度有很大影响。也即分离的类别顺序不同，整个模型的分类精度也不同。如果在某个节点上发生分类错误，该错误将扩展到下一个节点，后续分类的错误率将会越来越高。因此，有必要选择适当的结构，在这个结构下，先分出容易划分的类别（即与其他类别相差最大的样本），然后再分出不容易划分的类别。这样就尽可能将可能的错误远离根源，提高模型的准确率。

为解决上述问题，本文借鉴“聚类分析”的思想，采用类间距离法来确定二叉树的结构，具体思路如下：首先计算训练集数据各类别之间的距离，得到每个类别距离其他类的距离之和，并得到了每一类相距其他类的“远近顺序”，按照这个顺序建立了偏二叉树结构，然后沿着层级进行训练，并最终依次将各类分离开来。

本文使用计算相对简单的重心法来定义各类数据之间的距离。而两个类重心之间的距离采用欧式距离。假设训练集样本X包含k个类别，X1表示第1 类的训练集，X2表示第2类的训练集，X1和X2的样本数为N1和N2，都有p个特征向量，则X1和X2的样本重心分别为：

则Xi和Xj的样本重心的距离为：

选择样本重心距离其他类样本重心最远的类别作为第一个分离的类别，以此类推就确定了偏二叉树的分离顺序。

2 结合马田系统和SVM的多分类模型

由于SVM模型的两个参数会对故障模式分类的结果有很大的影响，因此对SVM 的参数进行寻优就很有必要了。并且本文所构建的SVM模型中可调参数有两个，分别是惩罚因子C和核函数的参数δ。本文通过比较分析，最终使用PSO 算法来进行SVM 模型的参数寻优。PSO优化SVM的具体步骤如下：

步骤1构建偏二叉树SVM 多分类结构，确定每个二分类器的初始特征空间，并使用马田系统的前半部分（正交表和信噪比）得到精简特征空间，从而构成了SVM多分类模型。

步骤2设置SVM 参数C和δ的范围。初始化粒子群算法的参数。确定种群数量、迭代次数、学习因子和权重，在解空间中随机生成粒子群。

步骤3将训练集的样本输入SVM 模型进行训练，以测试集模型整体的样类别预测准确率为适应度函数值。计算各粒子适应度并寻找当前最优粒子，确定个体最优和全局最优，将更新后的粒子适应度与最优适应度进行比较，选择更优的值。

步骤4监测模型是否达到预先设定的条件（适应度达到100%或者达到最大迭代次数），否则转步骤3。

步骤5对粒子所处的位置和速度进行实时更新。更新SVM的参数C和δ。

步骤6得到最优解，输出最优解对应的SVM 参数C和δ。

粒子群优化多分类SVM模型的流程图如图1所示。

图1 结合MTS和SVM多分类模型

3 实例计算

3.1 实验说明

本文采用的滚动轴承故障振动信号数据集来自于凯斯西储大学轴承故障模拟实验台。在实验初期，先采取电火花加工技术设置好故障点来假定轴承的故障发生。在型号为SKF 的轴承的不同部位预先设置故障点来分别模拟轴承内圈故障（Inner Raceway，IR）、外圈故障（Outer Raceway，OR）和滚动体故障（rolling Body，B）。在每个部位分别设置深度为0.18 mm、0.36 mm、0.54 mm的故障点，以模拟每个部位不同受损程度的故障（分别为轻微故障、中度故障和严重故障）。驱动端轴承故障数据采样频率为48 kHz，风扇端轴承故障数据采样频率则设置为12 kHz。通过16通道的DAT记录器采集振动信号，将原始数据保存为MATLAB 格式用于后期使用。

本文采用SKF驱动端轴承数据，外圈部位故障点为6点钟方向，转速为1 730 r/min，分别采集轴承正常状态和3 种故障类型的不同故障受损程度的振动信号。所以，一共采集到了10 个类型数据。其中每个类型数据包括100 个样本，每个样本信号中由1 024 个数据点所构成，这样就总共有10×100×1 024=1 024 000 个数据点。在每一类型数据中，训练集样本数量和测试集样本数量比值为3∶2，即采用随机抽取方式，将每一类型数据分为5份，选3份作为训练集样本，剩下2份作为测试集样本，这样方便之后的交叉验证。

3.2 信号处理

将采集的1 000个原始振动信号样本进行EEMD分解，均获得5个IMF分量和一个RES余量，图2展示了正常状态的EEMD信号分解图，图中按照频率高低将IMF分量从上到下依次排列，第一排是原始信号，最后一排是RES余量。由图可知，每种状态的振动信号均被分解成了5个IMF分量和一个剩余分量，并且每个IMF分量的图像是平稳的，说明了EEMD分解的良好效果。

图2 正常信号EEMD分解图

3.3 筛选敏感IMF

使用故障敏感IMF 选取方法可以挑选出对故障信息敏感的IMF分量。η取0.6，得到表1结果。

3.4 计算统计特征值

计算原始信号的能力熵特征以及各IMF 分量的时域特征和频域特征。时域特征有4 个，分别为均方根值、峰值、极差、峭度；频域特征有1 个，即频率标准差，即每个IMF 分量提取5 个特征量。各故障模式的原始信号经过故障敏感IMF 选择方法筛选了1～4 个不等的IMF分量，当对不同模式进行分类时要选择不同的IMF分量。当对正常样本进行分类时，选择4个IMF，这样就提取了21个特征值，构成了1 000×21 初始特征空间。

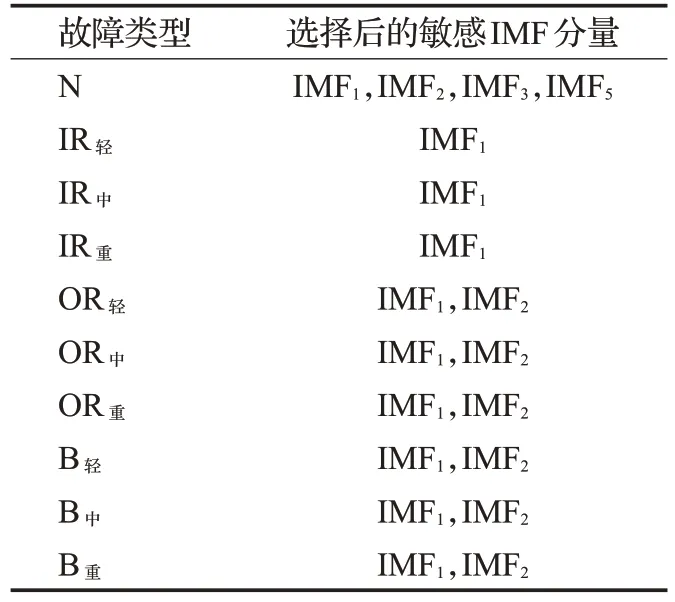
表1 故障敏感IMF选取方法结果

3.5 确定偏二叉树结构

当对未知的滚动轴承样本的故障模式进行类别预测时，首先判断故障类型，其次确定故障的受损程度。所以，先将训练样本分为四大类（正常样本、内圈故障、外圈故障和滚动体故障），通过偏二叉树分类器确定样本的故障类型；然后对每种故障类型再各分为三小类（轻微故障、中度故障和严重故障），分别使用偏二叉树分类器，确定故障的受损程度，这样就完成了马田系统故障模式多分类。

从每类故障模式随机选取60 个样本构成训练集，剩下40个样本构成测试集。为了方便计算类别重心距离，将训练集的特征向量个数都定为21。首先将训练集分为4 大类，分别为正常类和3 种故障类型。正常类样本构成为60×21，各故障样本构成为180×21，然后计算每一类的样本重心，最后计算各个类之间的欧氏距离，结果如表2所示。

表2 故障类型重心距离计算结果

距离其他类最远的类别先分离出去，由表2 可得，二叉树的分离顺序为正常类、滚动体故障、内圈故障和外圈故障，同理可得各故障类型的不同受损程度分离顺序。最终得到了马田二叉树多分类结构，如图3 所示。由图3 可以清晰地看出，一共需要构建9 个二分类器。第1～3 分类器可以判断故障类型，4～9 分类器可以确定故障受损程度。

图3 偏二叉树多分类结构

3.6 马田系统降维

通过前面章节的计算，得到了9 个SVM 分类器的初始特征空间。然后使用马田系统对每个特征空间进行降维，得到精简特征空间。表3是每个分类器的参数。

表3 信噪比增量图

3.7 粒子群算法优化SVM

使用粒子群算法优化SVM。在粒子群的寻优部分参数设置：种群数量20，学习因子c1=c2=2，惯性权重的值w进行线性递减，计算公式为：

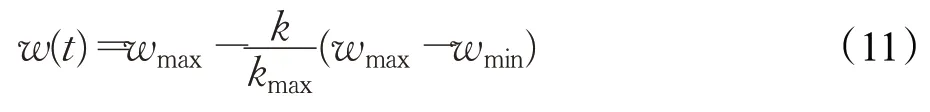
式中，wmax=0.4,wmin=0.1，k为目前迭代次数，kmax为最大迭代次数，kmax=100。

在 SVM 模型构建的参数设置：C∈(0.1,103),δ∈(0.1,200)，粒子维度为2。将训练集样本进行SVM模型训练，测试集样本进行测试，以确定适应度函数值。

3.7.1 故障类型寻优

当对故障类型进行分类时，图4 刻画了在测试时PSO寻优的过程，红色线代表每次迭代的最佳适应度的情况，当迭代到第23次时最佳适应度达到98.50%，之后就不再变化；蓝色线代表每次迭代的平均适应度的情况，分布在90%和97.75%之间，平均值为94.175%。通过寻优的过程得到了最佳的参数组合，即惩罚因子C为24.56，RBF 核函数参数σ为 5.58。所以，将 400 个测试集样本输入PSO 优化的SVM 模型，分类准确率达到98.50%（394/400），具体分类结果如表4所示。

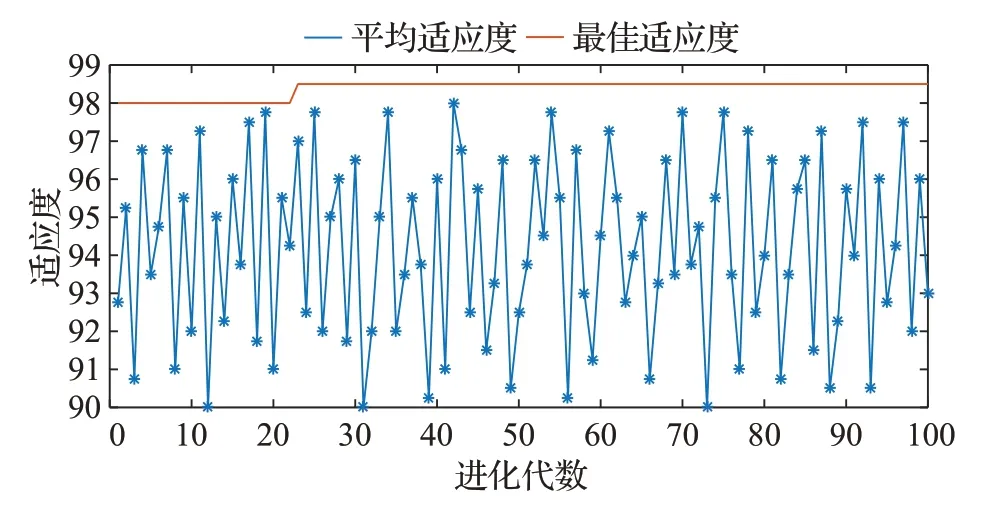
图4 PSO-SVM故障类型分类模型迭代适应度值

表4 故障类型预测结果

3.7.2 故障受损程度寻优

当对故障受损程度进行分类时，图5刻画了在测试时PSO寻优的过程，红色线代表每次迭代的最佳适应度的情况，在前17 次都处于95%，第18 次到37 次达到了95.75%，第38次时达到了96.5%，之后就不再变化；蓝色线代表每次迭代的平均适应度的情况，分布在84.25%和94.5%之间，平均值为90.807 5%。通过寻优的过程得到了最佳的参数组合，即惩罚因子C为16.82，RBF核函数参数σ为2.96。将400 个测试集样本输入PSO 优化的SVM模型，分类准确率达到96.5%（386/400），具体分类结果如表5所示。

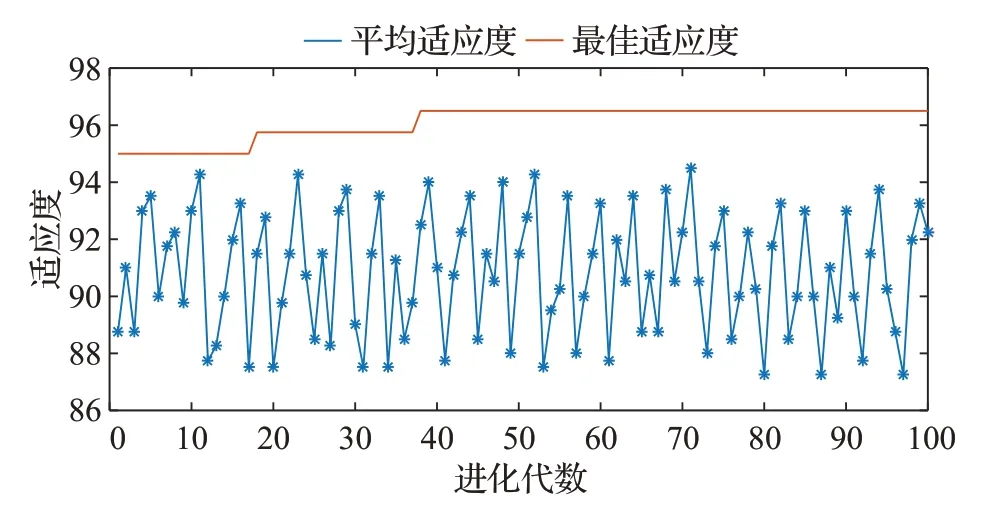
图5 PSO-SVM故障受损程度分类模型迭代适应度值

表5 故障受损程度预测结果

为了进一步分析误分情况，得到测试集的混淆矩阵，见表6。

表6 测试集混淆矩阵

由表4和表5可得，PSO-SVM多分类器对故障类型和故障受损程度的预测准确率都很高。由表6可得，误报率（即正常样本被错分为故障状态）为0，漏报率（即故障状态被错分为正常状态）也为0。从虚线框内可以看出3 种故障类型之间的错分率很低。故障受损程度之间的错分率也很低，说明该模型的有效性。

本文使用交叉验证，即将每种故障模式的100个样本随机分为5份，每份20个样本。轮流选择3份作为训练集，剩余2 份作为测试集，一共需要做C35=10 次实验。计算10 次分类结果平均值，即为该模型最终的准确率。经过10 次试验后，故障类型的类别预测准确率为97.90%，耗时34.7 s。故障受损的类别预测准确率为95.975%，耗时57.6 s。

4 对比分析

本文通过EEMD进行信号处理，得到一系列IMF分量，然后使用故障敏感IMF选取算法筛选出一部分IMF分量，然后从中提取出21 个特征值构成了初始特征空间。使用马田系统的前半部分，即正交表和信噪比进行特征约简，得到了精简特征空间。最后通过PSO优化的SVM进行故障模式多分类。为了验证本文所提出的方法的有效性，需要进行对比分析，每组实验都经过交叉验证。

（1）使用EMD 方法进行信号处理，其他方法不变，来验证EEMD 方法的有效性。预测结果如表7 所示。由实验1 和4 可知，EEMD 进行信号处理后模型的预测准确率高于EMD方法，说明了EEMD较EMD的优越性。

表7 特征生成方法对比分析

（2）为了验证故障敏感IMF 选取算法的有效性，对照组为全部IMF分量参与计算特征值，这样每个分类器的初始特征空间都是21 维。预测结果如表7 所示。由实验2 和4 可知，通过选取敏感IMF 分量可以有效提高分类模型的准确率。

（3）为了验证正交表+信噪比降维的有效性，对照组设置为不经过降维的过程，直接将初始特征空间输入到分类模型中。预测结果如表7 所示。由实验3 和4 可知，不经过降维的初始特征空间输入到多分类模型后准确率略低于正交表+信噪比降维，此组实验说明了特征降维是非常有必要的。

（4）对SVM 模型的两个参数进行寻优的方法有很多，如粒子群算法、网格搜索算法和遗传算法等，本文将这些分类方法进行比较，预测结果如表8 所示。由表8可知，未经优化的SVM 准确率远低于3 种优化SVM 的方法，但所用时间远少于3 种优化方法。在对3 种优化方法之间对比后发现，粒子群方法的准确率和效率都优于其他两种方法，说明了本文所提出方法的有效性。

表8 SVM寻优方法对比分析

5 结论

本文构建了结合马田系统和支持向量机的故障模式分类模型。首先利用EEMD 方法对原始振动信号进行分解，得到一系列IMF。经过故障敏感IMF选取方法筛选IMF 后计算其时域和频域特征参数以及原始信号的能量熵参数，构造初始的多维特征空间。接下来运用马田系统中的正交表和信噪比进行特征降维，得到精简特征空间。接下来使用偏二叉树方法构建支持向量机多分类模型。最后通过实验数据进行模型验证，结果表明该方法可以实现滚动轴承故障模式分类。主要结论有3个。

（1）运用故障敏感IMF选取方法可以有效筛选出与故障敏感度高的IMF，提高特征量空间合理性。

（2）马田系统可以高效地剔除冗余变量，使构建的精简特征空间更加的合理。

（3）构造了改进的偏二叉树SVM结构，并采用类间距离法来确定二叉树的结构，该结构可以高效地判断故障类型并确定故障的受损程度，提高模型的效率和预测精度。