融合粒子群与改进蚁群算法的AUV路径规划算法

朱佳莹，高茂庭

上海海事大学 信息工程学院，上海 201306

海洋资源已经成为人类开发的重点，但复杂的海洋环境对人类水下作业有着极大的限制，水下机器人正在成为海洋作业的主角，自主式水下机器人（Autonomous Underwater Vehicle，AUV）依靠自身携带的能源进行水下作业。由于在整个过程中无法补充能源，因此利用路径规划与安全避障技术对AUV 导航控制，是其能否精确、安全和完整地完成水下作业的关键。AUV路径规划问题已经成为了一个研究热点[1]，主要涉及两方面问题：一是对海洋环境进行三维建模；二是选取合适的算法进行全局路径规划。

海洋环境建模主要有两类方法：一类是规则地形模型，主要利用正方形、矩形等规则形状进行组合来表示海底表面；另一类是不规则地形模型，将三角形、多边形等不规则形状作为模型单元的基础[2]。文献[3]使用Voronoi图法简化三维水下环境，生成全局路线图；文献[4]将Delaunay 三角模型应用于被测地标，建立拓扑模型。文献[5]利用八叉树模型来反映AUV 工作环境，但主要应用于较大障碍物之间的路径规划，不适合存在许多小障碍物的环境；文献[6-7]不考虑水深，将三维空间简化为二维栅格模型，节省了空间，但却丢失了环境信息；文献[8-9]将三维空间划分为若干平面，然后利用二维栅格模型将每个平面栅格化，有效实现三维栅格建模。综上，文献[3-4]使用不规则地形模型，虽然能够真实地反映环境信息，但计算较复杂，占用较多空间。文献[5-9]采用规则地形模型，简单、计算量小，适用于三维路径规划问题，其中的栅格模型更适合与各种智能算法相结合。

路径规划算法可以归纳为以下四类：基于几何模型搜索的算法（Dijkstra、A*等）、基于概率采样的算法（概率路线图、快速拓展随机树等）、人工势场算法和智能算法（粒子群算法、蚁群算法、遗传算法、模拟退火算法、人工神经网络等）[2]。文献[10]使用A*算法求解最短路径规划问题，能在规划过程中及时中断和恢复，但其空间复杂度是指数级别的，不适合大规模复杂环境；文献[11]采用RRT*（Rapidly-exploring Random Trees）算法在线进行二维AUV 路径搜索，但随机性强，往往难以得到全局最优路径；文献[12]将人工势场算法与速度合成算法相结合，实现准确避障，但容易陷入局部最优解。文献[13]提出一种混合自适应蚁群算法（Ant Colony Optimization，ACO），有很强的全局搜索能力，但缺乏早期信息，收敛速度慢；文献[14]将粒子群算法（Particle Swarm Optimization，PSO）应用于路径规划问题，算法简单、初期收敛速度快，将它与蚁群算法相结合能够有效改善蚁群算法的不足。

近年来，AUV 路径规划与安全避障技术得到了快速的发展，但仍存在一些急待解决的问题，一是为简化处理，现有的水下机器人路径规划研究大部分没有考虑海拔信息，将三维环境简化为二维环境，无法满足海洋勘探的实际需要；二是现有的AUV 三维路径规划算法在面对复杂的实际问题时还存在计算复杂度大、路径规划效果不理想、不稳定等问题。

针对上述问题以及国内外研究现状，本文对AUV三维路径规划问题展开研究，采用三维栅格模型对真实海洋环境进行建模，将粒子群算法与改进蚁群算法相融合实现三维海洋环境中的AUV 全局路径规划，找出一条从给定起点到终点的最优或近似最优的无碰撞路径。

1 相关模型

实现水下路径规划包括两方面的基础：一是对AUV 所处的海洋环境建模，将水下环境信息转化为一种计算机能够识别的表达方式；二是对AUV 三维路径规划问题建立路径评价模型，用来衡量路径的好坏，也可以看作本文优化问题的目标函数。

1.1 海洋环境模型

建立海洋环境模型是实现AUV路径规划的前提条件，下面先介绍本文真实海洋环境数据的获取方式；再介绍基于空间分层思想建立三维栅格模型并进行海洋环境建模；最后介绍如何在该环境模型中实现路径规划任务。

1.1.1 真实海洋环境数据的获取

目前有多种海洋环境开源数据库，本文使用的海底地形数据来源于全球海陆数据库（General Bathymetric Chart of the Oceans，GEBCO）。在 GEBCO 地图上选取某海域进行采样，形成采样矩阵，下载可以得到采样矩阵中各点的海拔数据，并使用环境建模方法对获取的环境数据进行建模。

1.1.2 真实海洋环境数据三维栅格建模

海洋环境模型需要在采样得到的海洋环境上建立三维空间坐标系，如图1所示。

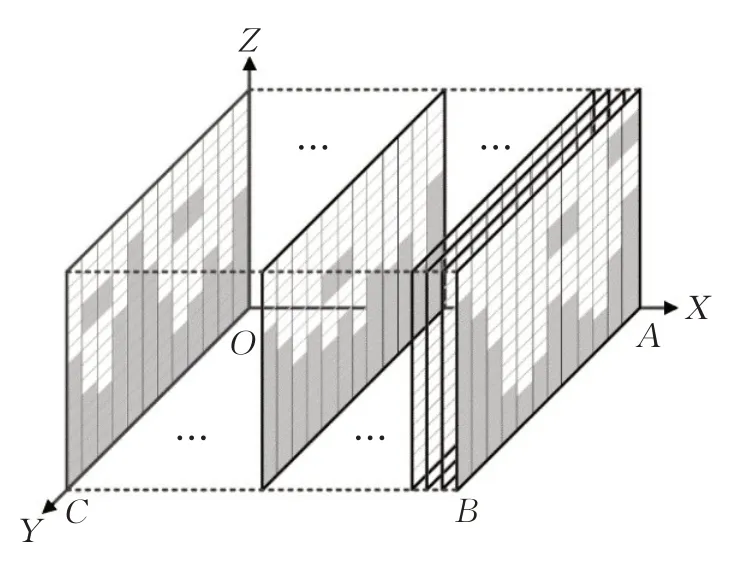
图1 三维栅格环境模型示意图

其中，X轴、Y轴分别表示水域的长度和宽度，Z轴表示海拔高度，OABC 表示AUV 整个工作区域。沿X轴将三维空间等距离切片分层，每个YOZ平面都是一个二维栅格平面，对平面上的每个栅格进行考察，小于等于该处海底海拔值的栅格为障碍栅格，标记为0，其余为自由栅格，标记为1。通过若干层二维栅格，最后组成三维栅格来表示整个海洋环境。除海底山脉外，本文还随机产生了若干悬浮球形障碍来模拟真实海洋环境，并将对应位置处的栅格标记为障碍栅格。最终，AUV 工作环境由一个三维0-1矩阵表示。

1.1.3 路径规划算法在三维栅格模型中的实现

三维栅格模型中引入了空间分层的思想，将整个AUV 工作空间均匀划分为N个二维栅格平面。令起点和终点分别设置在第一层和最后一层平面上，则一条完整的路径必定与每一层平面都会有一个交点，由此，AUV 路径规划问题可以转化为在N-2 个中间栅格平面上分别求一个最优中间路径点的问题。

若要将路径规划算法应用于该三维栅格模型中，也必须融入这种空间分层思想。本文路径规划算法均为智能算法，先在中间每层平面上随机选取一个中间路径点的位置，再通过多轮迭代的不断学习，最终依靠群集智能收敛到最优中间路径点附近，将所有路径点相连即为求得的最优路径。

1.2 路径评价模型

从给定起点P1开始，经过若干中间路径点P2,…,PN-1,最后到达给定终点PN，将这些路径点相连，得到一条完整路径path，即为一个可行解，解的形式如式（1）所示：

对于所有可行解，必须建立一个路径评价模型来评估路径好坏[15]。本文综合考虑路径长度、崎岖性和危险性等指标。

1.2.1 路径长度

路径长度是路径规划问题首要考虑的一个因素，其计算如式（2）所示：

式（2）中，Pi表示第i层栅格平面上路径点的坐标(i,yi,zi)；‖Pi+1-Pi‖ 表示Pi与其下一路径点Pi+1之间的距离，其距离度量采用欧氏距离计算；N为路径点总数。对所有路径段距离求和得到总的路径长度，该值越小则路径越短。

1.2.2 路径崎岖性

由于AUV 携带能源有限，过多的起伏会导致能源的快速消耗，因此希望规划的路径尽可能平滑。路径崎岖性通过式（3）计算：

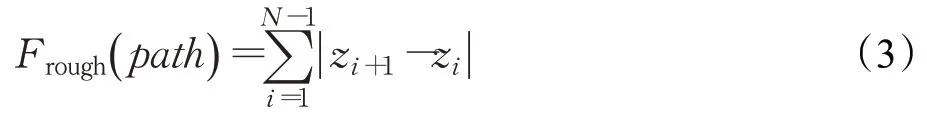
式（3）中，|zi+1-zi|表示Pi到下一路径点Pi+1深度方向的位移，为简化计算，将所有求和，近似表示路径的崎岖程度。该值越小则路径越平缓。

1.2.3 路径危险性

由于AUV 在实际的航行过程中难免存在误差，路径越贴近障碍物则潜在的风险就越大，所以将路径周围的危险性也作为一个评价因素，主要考察距离路径两个栅格范围内的障碍物情况，其余较远的障碍物假定不会威胁到AUV。路径危险性的计算如式（4）所示：

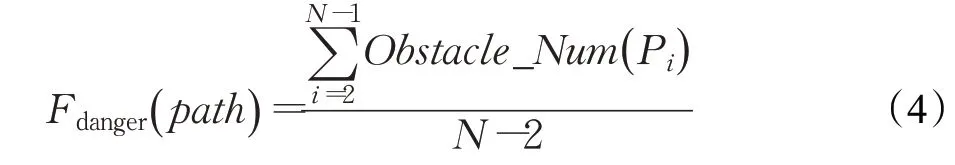
式

（4）中，Obstacle_Num(Pi)表示距离Pi两个栅格范围内的障碍物总数；Fdanger(path)表示一条路径上每个路径点周围平均存在的障碍物个数，该值越小则路径越安全。

在环境建模阶段可以预先计算每个栅格周围的障碍物数量，存储在一个三维矩阵中，在路径规划阶段直接调用，可以减少算法的运行时间，提高运行效率。

针对上述三个评价指标，为了将多目标的优化问题转化为单目标问题进行求解，先使用min-max标准化方法对求得的三个指标值分别做归一化处理，再对三者加权求和得到总的路径评价值，该值越小则说明规划出来的路径越好，将其作为路径评价函数，并求其最小化，具体计算如式（5）所示：

2 PSO-ACO路径规划算法

本章将具体介绍本文所提出的AUV三维路径规划算法（PSO-ACO），先使用粒子群算法预搜索路径，其结果用来优化蚁群算法的初始信息素；然后再对蚁群算法的状态转移规则、信息素更新方式作出进一步改进，并加入奖惩机制，实现AUV全局路径规划。

PSO-ACO路径规划算法流程如图2所示。

图2 PSO-ACO算法流程图

2.1 粒子群算法预搜索路径

传统蚁群算法将每个路径点上的初始信息素设定为一个常值，蚂蚁在搜索初期将等概率地从周围可行点集中选择一个路径点走，蚂蚁需要迭代更多次，才能在不断尝试中找到一条完整路径，这也是传统蚁群算法初期收敛速度慢的主要原因之一。

为解决初期收敛速度慢的问题，引入粒子群算法，利用其初期收敛速度快的特点，与蚁群算法互补。先使用粒子群算法快速预搜索路径，再将每个粒子路径上的初始信息素提高，从而加强蚁群算法初期的搜索能力。

2.1.1 粒子群算法路径预搜索原理

粒子群算法用粒子表示可行解，一个粒子表示一条路径。一开始，粒子群初始化为一组随机解，每个粒子有速度、位置两个属性。每一轮迭代中，通过计算每个粒子的路径评价值来更新个体最优解和全体最优解，然后再依据这两个变量不断更新自己的速度和位置。通过多轮迭代，最终粒子群将聚集到最优路径四周，实现路径预搜索任务。

假定粒子群规模为m，则第t轮迭代粒子群的位置、速度矩阵如式（6）、式（7）所示：

由式（6）、式（7）可知，第t轮迭代中粒子i在第j层栅格平面的位置坐标和速度向量分别为和。

粒子i的速度、位置更新分别如式（8）、式（9）所示：

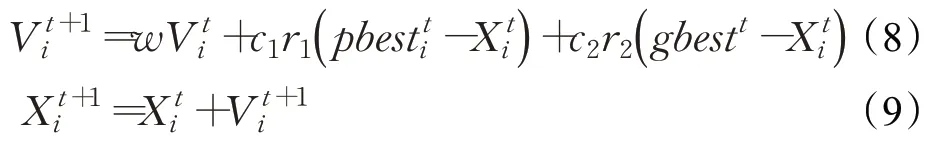
式（8）、式（9）中，表示粒子i在第t轮迭代的个体最优解；gbestt表示第t轮迭代的全体最优解；w为非负的惯性因子，其值越大表示全局搜索能力越强；c1和c2为学习因子；r1和r2为介于( 0,1) 之间的随机数。

个体与全体最优解的更新分别如式（10）、式（11）所示：

式（10）、式（11）中，i=1,2,…,m，m为粒子群规模。

2.1.2 粒子群算法路径预搜索策略

粒子群算法预搜索路径时，仍需考虑以下几点：第一，粒子在更新位置过程中很有可能会导致路径穿越障碍物，所以在计算路径评价值时要加入一定惩罚；第二，为了简化算法，在预搜索过程中，暂时不考虑悬浮障碍物；第三，该算法最后并不是输出一个最优解，而是输出所有粒子最终所在的路径，以提高这些位置的初始信息素。因此对于粒子群规模和它们最后的收敛程度也有一定要求，粒子群规模按照环境规模进行调整，粒子群最后的收敛程度通过调整参数来控制，既不能使粒子群几乎完全收敛于最优路径附近，又不能使粒子群太过发散。

通过PSO 路径预搜索，使蚁群算法在开始前，其初始信息素已有较好分布，算法初期寻径能力极大加强。且由于PSO算法执行速度快，加上路径预搜索无需等到算法完全收敛，因此，将ACO 与PSO 相结合，算法的收敛速度反而更快，算法的复杂性也不会很高。

2.2 改进蚁群算法全局路径规划

蚂蚁走过的路径点集合代表一个解，路径越优则蚂蚁在该路径上留下的信息素就越多。随着迭代次数的增加，越好的路径上累积的信息素越高，蚂蚁走这条路的几率就越大，最终在正反馈的作用下，蚂蚁会逐渐收敛到最优路径上。

PSO-ACO 的蚁群算法部分，除了导入优化后的初始信息素之外，还对传统蚁群算法做出三方面改进，具体改进措施将在下面三小节进行介绍。

2.2.1 状态转移规则改进

蚂蚁根据状态转移规则来选择下一路径点，传统状态转移规则的思想是先确定下一步所有可行点并计算它们的转移概率，然后根据轮盘赌原则，从所有可行点中选择一个点作为下一路径点。可行点转移概率的计算如式（12）所示：

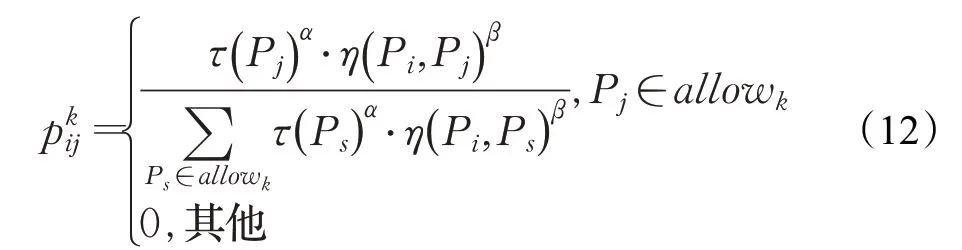
式（12）中，表示蚂蚁k从Pi移动到Pj的概率；τ(Pj)表示Pj上存储的信息素浓度；η(Pi,Pj)表示Pi到Pj的启发信息；allowk表示蚂蚁k的可行点集合；α和β分别表示信息素和启发信息在蚂蚁寻径中的重要程度，本文令α=β=1。易知，信息素和启发信息加权乘积越大的可行点被选择的概率就越大。

虽然这种轮盘赌的选择方式能有效保证路径的多样性，但也存在着一些弊端。实验发现，由于每个可行点的信息素和启发信息加权乘积的差距没有那么大，以至于轮盘赌只有小概率会选择当前最优的可行点，导致算法收敛速度缓慢。为此，对状态转移规则做出改进，具体如式（13）所示：

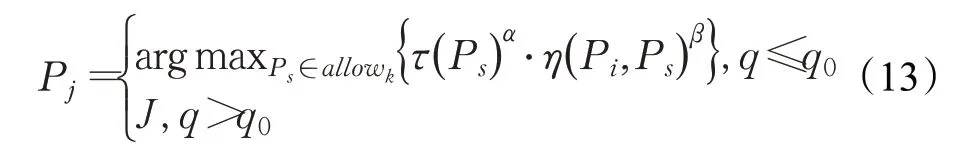
式（13）中，Pj表示下一个被访问的路径点；J表示根据式（12）按概率选择出来的下一路径点；q0为( 0,1) 之间的一个给定阈值，以此来调节算法对新路径的探索能力，本文令q0=0.1。

改进后，算法有更大的机会选择信息素和启发信息加权乘积最大的点作为下一路径点，加快了算法的收敛速度。通过实验验证，在本文设定的阈值下，不会妨碍算法对新路径的探索能力，仍保证了路径的多样性，不会导致算法易陷入局部最优。

2.2.2 信息素更新方式改进

信息素更新方式主要有两种：一种是信息素全局更新，在每轮迭代结束时进行。好路径上的信息素将越来越高，坏路径上的信息素将越来越低，以此提高蚂蚁往好路径上走的概率；另一种是信息素局部更新，蚂蚁每走一步就对该路径点上的信息素做挥发处理。通过降低蚂蚁走过路径上的信息素，来保证同一轮迭代中蚂蚁不会集中在某条路径上，而会尝试走不同路径，保证当轮迭代中路径的多样性。

信息素全局更新公式如式（14）、式（15）所示：

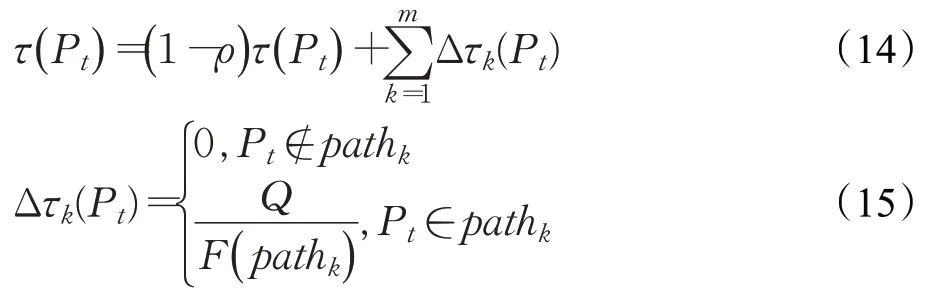
信息素局部更新公式如式（16）所示：

式（14）～式（16）中，τ(Pt)表示Pt上的信息素浓度；ρ表示信息素挥发因子；Δτk(Pt)表示蚂蚁k对Pt的信息素增量；Q为常数；pathk表示蚂蚁k的路径。

在这里，两个变量是动态变化的：

第一，信息素增量动态变化。由式（15）可知，令Δτk(Pt)随路径评价值变化，路径越好，增量越大。

第二，信息素挥发因子ρ也是动态变化的，如式（17）所示：

式（17）中，T表示当前迭代次数；Tmax表示最大迭代次数。根据信息素在路径规划不同阶段的重要程度，可以分成三部分：规划初期，由于PSO 预搜索已经得到了较好的初始信息素分布，此时蚂蚁主要依靠初始信息素寻径，令ρ取较小值；规划中期，令ρ变大，加强算法对新路径的探索能力，让信息素不会堆积在个别路径上而导致蚂蚁只往这些路径走；规划后期，路径基本探索完毕，为尽早收敛，所以ρ再取较小值。

2.2.3 加入奖惩机制

定义能够顺利到达终点的蚂蚁为活蚂蚁；不能顺利到达终点的蚂蚁为死蚂蚁。对死蚂蚁加入惩罚，降低其路径上的信息素，降低后面蚂蚁选择该路径的概率；对活蚂蚁加入奖励，提高其路径上的信息素，增加后面蚂蚁选择该路径的概率。

通过加入奖惩机制，可以很大程度上避免后续蚂蚁陷入死区，提高每轮迭代中蚂蚁的存活率，即每轮迭代中产生有效解的个数，这样就更可能找到更优的路径去不断刷新全局最优解。

3 实验结果分析

为验证本文改进算法在解决AUV三维路径规划问题上的可行性和有效性，本章选取了两个不同规模、不同地形的海洋环境进行实验。通过PSO-ACO与其他智能算法的对比，分析几种算法在本文问题上的表现及PSO-ACO算法的改进效果。

3.1 实验数据及实验环境

从GEBCO全球海陆数据库中选取的两个海域分别为：一个为较小规模平缓海域，坐标（Lng：27.512 5，Lat：123.000 0），采样矩阵大小为50 km×50 km；另一个为较大规模复杂海域，坐标（Lng：40.050 0，Lat：154.000 0），采样矩阵大小为100 km×100 km。令海域最深的点作为Z=0 处，其他位置的Z值依据这个确定。起点和终点分别取在两个对角。

实验的硬件环境为Intel Core i7 处理器，8 GB 内存，操作系统为Windows 10，算法使用Matlab实现。

3.2 较小规模平缓海域仿真实验

本节的实验环境为较小规模平缓地形，主要考察算法在简单环境下是否能达到预期效果。

PSO-ACO算法的参数设置如表1、表2所示。其粒子群算法部分，由于实验环境规模较小，将粒子群规模设为500，v的范围设为[-10,10]。通过实验不断调整其余参数，最终选取c1=c2=2，w=0.6，最大迭代次数为100；其蚁群算法部分，同样因为较小规模的实验环境，将蚂蚁规模设置为50。实验发现ACO 总能在150次迭代之前收敛完全，因此，将150 定为最大迭代次数。通过实验验证，将权值α和β设为1。ρ和τ0由于算法的改进，这里不再为一个常值。

表1 较小规模实验PSO-ACO中粒子群算法参数设置

表2 较小规模实验PSO-ACO中蚁群算法参数设置

将PSO-ACO 算法与蚁群算法、粒子群算法和遗传算法进行对比实验，结果如图3所示。

其具体的仿真结果数据如表3所示。表3中第二到第四列为路径评价模型的三个指标，F值为综合下来的路径评价值，本文通过多次实验，确定三个评价指标的权重如下：w1=0.5、w2=0.2 和w3=0.3。从实验结果可以发现：GA算法由于交叉变异等操作，使得有些相邻的路径点之间水平和垂直方向变化较大，路径崎岖程度明显大于其他算法，且算法运行时间14 s 之久，它需要迭代更多次才能找到较优解；PSO算法虽然收敛运行时间最短，但多次实验表明，该算法不够稳定，易早熟收敛、陷入局部最优；ACO 算法全局搜索能力良好，但收敛迭代次数较多，算法运行时间较长；本文算法规划的路径在三个指标上都是较好的，且收敛迭代次数和运行时间也有优势，综合性能最佳。

图3 较小规模实验四种智能算法规划的路径

表3 较小规模实验四种智能算法的仿真结果

为了更好地展示PSO-ACO 算法对ACO 算法的优化效果，这里进一步提取了两种算法在仿真实验中的收敛曲线，对比如图4所示。

图4 较小规模实验PSO-ACO与ACO的收敛曲线

除了改进后动态变化的部分，PSO-ACO和ACO算法的参数设置保持一致。从图4 可以发现，规划初期，PSO-ACO 算法寻径能力明显提高，迭代25 次就能找到第一条完整路径，而ACO 算法要迭代58 次。这主要是因为PSO-ACO 的初始信息素得到了优化，其粒子群算法的预搜索结果如图5所示。

而规划中期，PSO-ACO 算法能更频繁地找到更优解；规划后期，PSO-ACO 算法也能更早收敛，且最终找到的路径比ACO算法的更优。综上，PSO-ACO算法对ACO算法的改进是可行、有效的。

3.3 较大规模复杂海域仿真实验

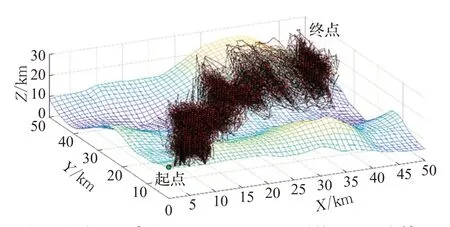
图5 较小规模实验PSO-ACO中粒子群算法预搜索结果

为了考察上述算法是否能适应不同环境，这里选取了规模更大、地形更复杂的海洋环境做进一步实验。

PSO-ACO算法的参数设置如表4、表5所示。其粒子群算法部分，由于实验环境变大，将粒子群规模调整为1 000，v的范围调整为[-20,20]。通过实验验证，其余参数保持不变；其蚁群算法部分，在较小规模实验参数设置的基础上，通过实验发现ACO总能在500次迭代之前收敛完全，因此，将最大迭代次数调整为500。

表4 较大规模实验PSO-ACO中粒子群算法参数设置

表5 较大规模实验PSO-ACO中蚁群算法参数设置

四种算法在较大规模实验中的规划结果如图6所示。

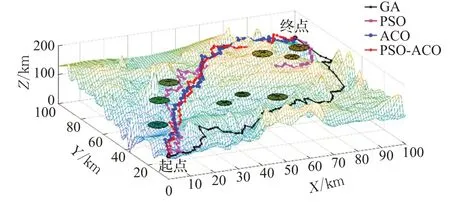
图6 较大规模实验四种智能算法规划的路径

其具体的仿真结果数据如表6所示，这里同样通过多次实验确定了路径评价模型的三个权重，分别为：w1=0.5、w2=0.2 和w3=0.3。

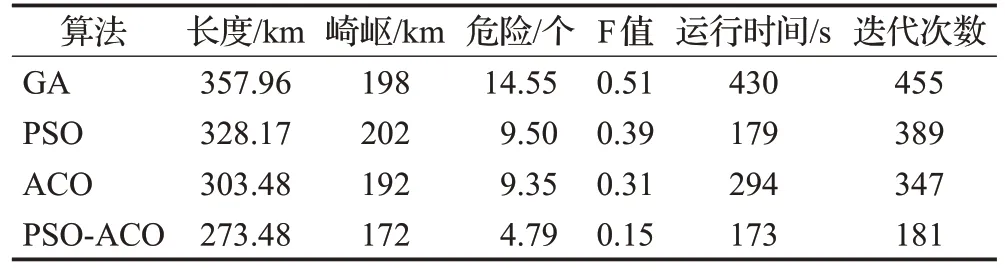
表6 较大规模实验四种智能算法的仿真结果

通过实验，发现GA 算法局部搜索能力较弱，在较大规模复杂环境下需要430 s 才能得到较优解，明显慢于其他算法，且得到的路径也不佳；PSO 算法执行速度依然较快，但是它对初始粒子群有一定依赖性，在较大规模复杂环境中更容易陷入局部最优，算法效果并不够稳定；ACO算法在复杂环境中相较于其他智能算法，其综合表现良好；PSO-ACO 在较大规模复杂环境中表现更加突出，算法稳定，规划的路径最优且耗时最短。

PSO-ACO与ACO的收敛曲线对比如图7所示。

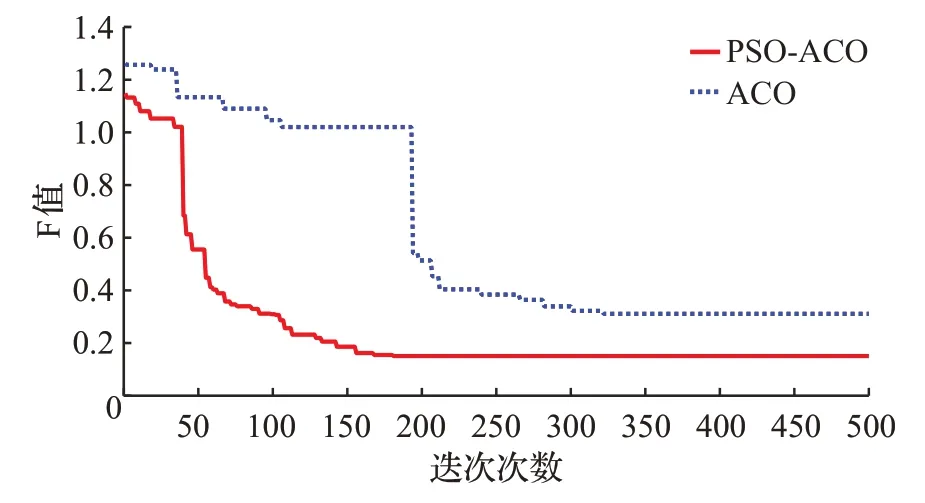
图7 较大规模实验PSO-ACO与ACO的收敛曲线

PSO-ACO的粒子群预搜索结果如图8所示。

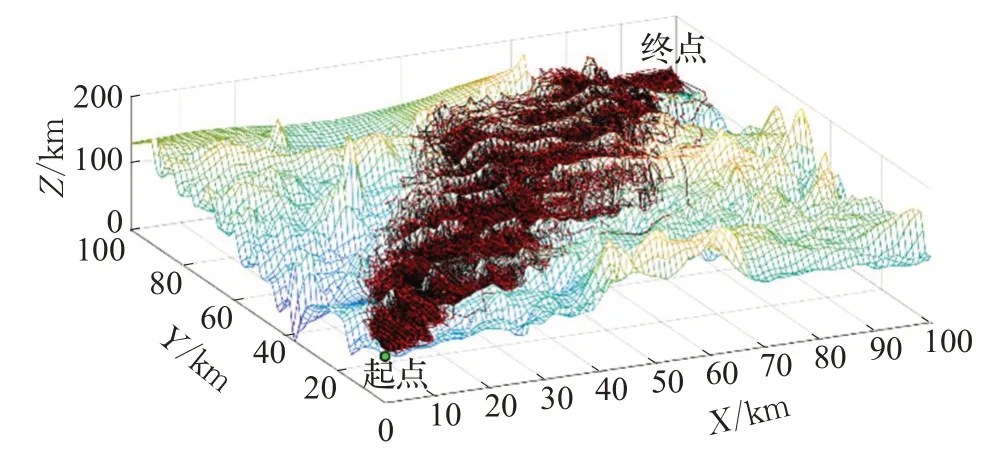
图8 较大规模实验PSO-ACO中粒子群算法预搜索结果

由图7、图8可知，PSO路径预搜索在复杂环境中依然有效。PSO-ACO 的寻径能力、算法收敛速度等各方面都有了明显的提高，PSO-ACO算法对ACO算法的优化在较大规模复杂环境下依然有效，且更加突出。

4 结束语

本文研究AUV 三维路径规划问题，提出粒子群与改进蚁群算法相融合的AUV路径规划算法。使用三维栅格模型对海洋环境建模，综合考虑路径长度、崎岖性、危险性三方面来衡量路径好坏来建立路径评价模型。采用粒子群算法预搜索路径优化初始信息素，再使用改进蚁群算法进行全局路径规划。实验结果表明，本文的改进算法比起蚁群算法和其他智能算法具有更良好的全局搜索能力，迭代次数更少，收敛更快，耗时更短，最终得到的路径更优。但由于算法基于空间分层思想，在每个二维栅格平面选取一个中间路径点，从而导致规划得到的路径拐点较多，且为折线，对AUV来说会产生更大的能耗。

下一步，可以对规划出来的路径去除冗余拐点并进行平滑处理。其次，可以对环境模型做进一步优化，使其更大程度上接近真实海洋环境。