考虑轴向变形的谐波减速器柔轮中面位移计算*
2021-03-23范元勋
赵 彬,范元勋
(南京理工大学 机械工程学院,江苏 南京 210000)
0 引 言
随着计算机科学、仿生学、人工智能等学科的进步,机器人技术如今正处于蓬勃发展的阶段。作为机器人的核心部件,精密减速器占整机的三分之一以上[1],谐波减速器因其大传动比、高精度、小体积等优点受到了广泛的关注与研究。比如日本的ASIMO机器人有20多个关节采用了谐波减速器,WABIAN-2机器人的所有关节全部采用了谐波减速器进行传动[2]。
在谐波减速器中,柔轮筒体受波发生器强迫变形后与刚轮进行啮合传动,随着波发生器的旋转,柔轮筒体上产生与旋转周期相对应的交变应力。因此,相较于其他零件,柔轮极易遭到破坏,极大地影响到谐波减速器的性能。目前,柔轮的应力状况受到了研究人员的广泛关注。根据弹性力学知识,只需求得筒体的位移,则其应力也将迎刃而解。但由于柔轮变形的复杂性,柔轮筒体上各点的位移往往难以有较为准确的计算方法。
李秋芳[3]用一对方向相反的径向集中力代替波发生器进行了柔轮的变形力计算,这与实际的接触方式有较大差异,得到的径向变形力过大;杨勇[4]根据柔轮中线不伸长假定,通过对柔轮中线变形前后的弧长积分表达式进行处理,得到了中线上各点的位移转角;邢静忠[5]为减小现有的力学小变形假定下位移叠加产生的偏差,对包角内的中面曲线采用了凸轮等距曲线来确定,对包角外曲线利用曲率连续条件构造样条函数来表示;GRAVAGNO[6]得到了柔轮中面与波发生器轮廓的运动误差表达式,为计算柔轮筒体中面提供了一种思路;MAHANTO B S等人[7]用有限元软件分析了不同波发生器对柔轮的装配应力的影响;阳培[8]通过有限元仿真方法,对柔轮初始变形力与各个参数的关系进行了数值化分析与曲线拟合,有限元软件虽然能较好地反映柔轮的变形的情况,但难以得出各参数对变形的解析结果,只能为每一个模型单独进行建模分析;MA[9]设计了一种用激光位移传感器来测量柔轮筒体径向位移的装置,分析了转速对形变的影响,为柔轮变形理论提供了实验依据。
上述的理论研究中,大多是将柔轮筒体的变形问题当作平面问题来处理,而忽略了筒体沿轴向的位移变化;因此,这种研究结果和柔轮的实际变形必然有着较大的差别。
通过查阅文献和多次的有限元研究结果发现,波发生器与柔轮筒体的接触是一圈很窄的环形范围,相较于一对集中力,一圈径向线载荷能更加适合地来体现波发生器对柔轮筒体的作用力。因此,本文用一圈径向线载模拟波发生器对柔轮的作用,对柔轮中面的位移进行计算,并通过有限元来验证理论计算结果的正确性。
1 柔轮变形模型的建立
由于柔轮齿圈的存在使得直接建立柔轮模型特别复杂,考虑到柔轮筒体壁厚远小于筒体半径,笔者将柔轮筒体简化为一个薄壁圆柱壳,用一圈线载荷来模拟波发生器对柔轮筒体的作用,进行接下来的分析。
柔轮受力模型简化图如图1所示。
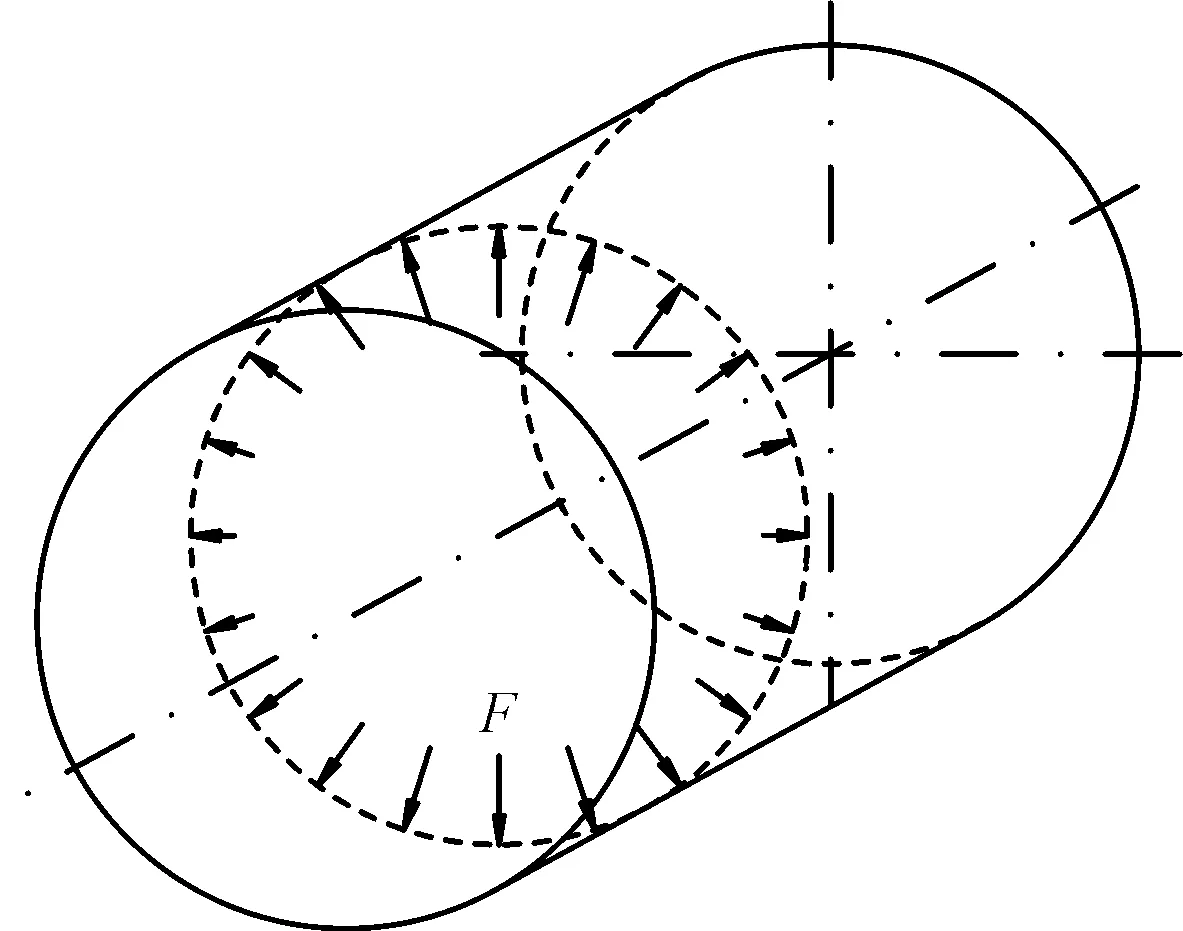
图1 柔轮受力模型简化图
笔者摒弃了以往研究中令中面各向应变为0的小变形设想,做出如下假设:
(1)不考虑加工工艺对柔轮材料的影响,将柔轮视为各向同性体;
(2)波发生器与柔轮的接触视为一圈线接触,边界位于波发生器最深入柔轮的一侧;
(3)柔轮筒体在变形过程中其壁厚不发生改变。
笔者将圆柱壳放在曲线坐标系αβγ中,把α坐标放在柱面母线方向;β坐标放在准线方向,γ坐标放在径向。中面沿α方向曲率k1=0;中面沿β方向曲率k2=1/R,其中,R为柔轮筒体中面半径。
将α为常量的横截面记作α面,将β为常量的横截面记作β面,中面横截面上的内力如图2所示。
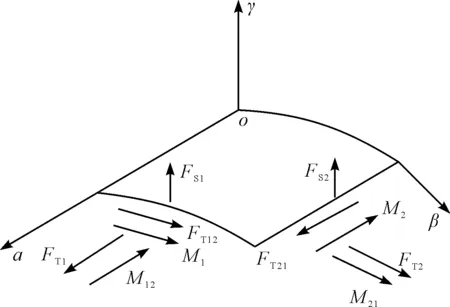
图2 筒体中面横截面内力图FT1—α面上单位长度拉压力;FT2—β面上单位长度拉压力;FT12—α面上单位长度平错力;FT21—β面上单位长度平错力;M1—α面上单位长度弯矩;M2—β面上单位长度弯矩;M12—α面上单位长度扭矩;M21—β面上单位长度扭矩;FS1—α面上单位长度横向剪力;FS2—β面上单位长度横向剪力
根据弹性力学知识,不难得到柱壳中面的平衡微分方程和弹性方程[10]。
其中,微分方程为:
(1)
式中:u,v,w—弹性体内任意一点分别沿α、β、γ的位移分量;μ—柔轮材料的泊松比;E—柔轮材料的弹性模量;b—柔轮筒体壁厚;q1,q2,q3—柱壳分别沿α(纵向)、β(环向)、γ(径向)所受的载荷分量。
弹性方程为:
(2)
式中:D—薄壳的弯曲刚度,D=Eb3/12(1-μ2)。
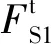
对于柔轮变形问题,柔轮所受的载荷主要是径向载荷,在式中令q1=q2=0;同时,为方便计算,引入位移函数F=F(α,β),把中面位移表示成为:
(3)
则式中的前两个方程总能满足,第3个方程则变为:
(4)
再将该式代入弹性方程中,得到用位移函数F表示的内力表达式:
(5)
因为柔轮筒底变形量很小,将其视为圆形薄板小挠度进行分析;将筒底放置在同一曲线坐标系αβγ中。筒底的各个内力如图3所示。

图3 柔轮筒底中面内力图
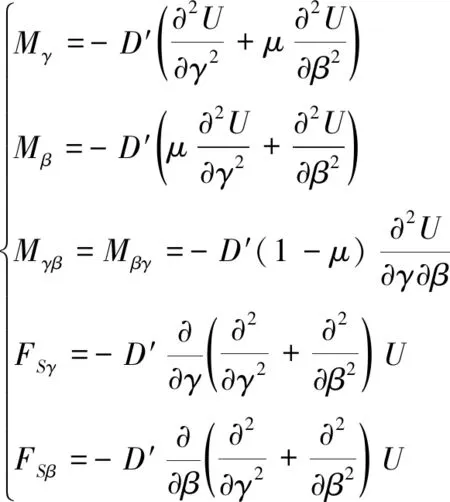
(6)
式中:U—柔轮筒底上各点沿α方向的位移函数;D′—柔轮筒底的弯曲刚度,计算方法和筒体的相同,只需要将厚度b替换成筒底厚度即可。
同样,有筒底的弹性曲面微分方程为:
(7)
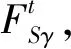
2 位移函数的求解
当圆柱壳受线载荷作用时,径向载荷q3仅作用在α=α0处,而不再是普通问题中的连续函数,所以在式中引入Dirac函数δ(α-α0):
(8)
对于方程不容易求得通解,故笔者通过构造Green函数G(α)来求解。
考虑到柔轮的变形是轴对称的,所以此处位移函数F是一个偶函数。设方程的解为:
(9)
式中:α1—筒体和筒底相交的边界;α2—筒体外口边界。
式(9)可以表示为:
(10)
Green函数的定义为:
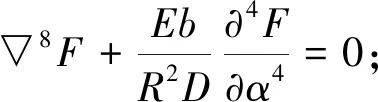
(2)Gn(α,α0)在α1≤α≤α2中,使F(α,β)满足所有的边界条件;
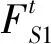
柔轮与椭圆波发生器的接触线载荷分布规律近似余弦分布[11],所以此处假设径向线载荷q3=qcos(2β/R),其中,q为载荷峰值。
由于位移函数F(α,β)是级数形式,此处把上式右侧也展开为级数形式,可得到:

(11)
将其代入到式左侧,可得到:
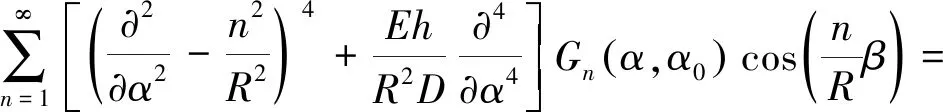
(12)
通过观察式,分析其解应具有的形式后,设G1n为α<α0的Green函数,G2n为α>α0的Green函数,其表达式如下:
(13)

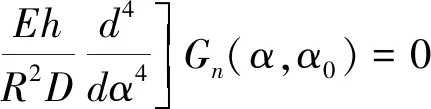
由此得到了与G1n、G2n相对应的位移函数F1和F2。根据Green函数的定义(3)和边界条件可以得到:
(14)
再考虑α1和α2两处的边界条件,笔者将柔轮筒体的两端视为自由端,则在边界上有:
(15)
式(14,15)一共16个方程,用计算机编程联立求解出16个系数关于q的代数表达式,再利用α=α0,β=0处的径向位移w等于理论设计的最大径向变形量这一条件,计算出q的值,将16个系数和q代入式(13)和式(10),就得到了位移函数F1(α,β)和F2(α,β)的初步结果。
从结果可以发现,当n≠2时,式(12)左边恒为0,此时无论16个系数如何取值等式恒成立,所以仅当n=2时该计算有意义,可以用n=2时的位移函数代替整个级数,即F1(α,β)=G12(α)cos(2β/R),F2(α,β)=G22(α)cos(2β/R)。
因为α=α1的边界处壳体并不是完全自由的,该结果是初步结果,还需要进一步对它进行修正。
为保证柔轮筒底和筒体之间的位移协调,有u(α,β)|α=α1=U(γ,β)|γ=γ2,其中:γ2—筒底与筒体重合边所在位置的γ值。所以此处假设:
(16)
式中:g(γ)—关于γ的未知函数。
将式(16)代入式(7)得到一个关于γ的4阶微分方程,再根据4个边界条件U|γ=γ1≡0,∂U/∂γ|γ=γ1≡0,U|γ=γ2=u|α=α1,∂U/∂γ|γ=γ2=∂u/∂α|α=α1就能计算出U(γ,β)的表达式。
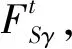
3 实例计算
为验证本文提出的计算模型的准确性,笔者在ABAQUS中以波数为2的谐波减速器柔轮进行变形的有限元仿真分析。
柔轮的结构及相关参数如图4所示。
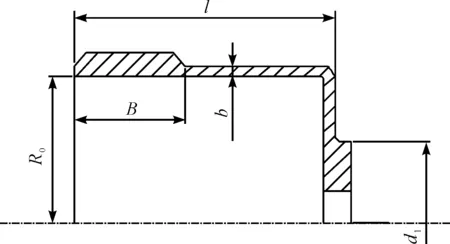
图4 柔轮结构及参数图R0—筒体内径,为36 mm;B—波发生器宽度,为13 mm;b—壁厚,为0.65 mm;d1—筒底法兰外径,为46mm;l—筒长,为72 mm。
柔轮材料弹性模量E取209 000 MPa;泊松比μ取0.3;波发生器设置为刚体,网格类型为C3D20。
令柔轮筒体中面半径R=R0+b/2,将上述相关参数代入式中,得到假设的Green函数G1n与G2n;然后将其代入式(14,15)中进行待定系数的求解。其中,为方便计算,将一圈径向线载荷作用位置α0放置在α=0处,根据筒体总长度l=72 mm,波发生器宽度B=13 mm,则相应地得到α方向的边界分别为α1=-59和α2=13。
在后续的迭代过程中,杯底的边界分别为γ1=d1/2,γ2=R。由此可得到理论计算的位移函数为:
(17)
将柔轮筒体的u、v、w3个方向位移的理论结果和有限元结果分别进行比较,分别如图(5~7)所示。
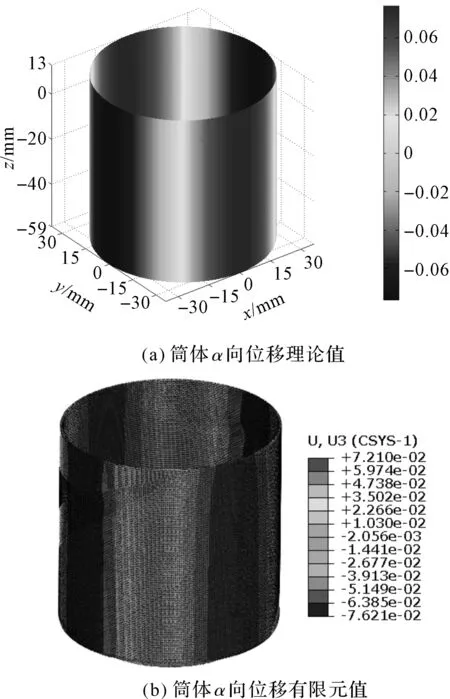
图5 柔轮筒体α向位移
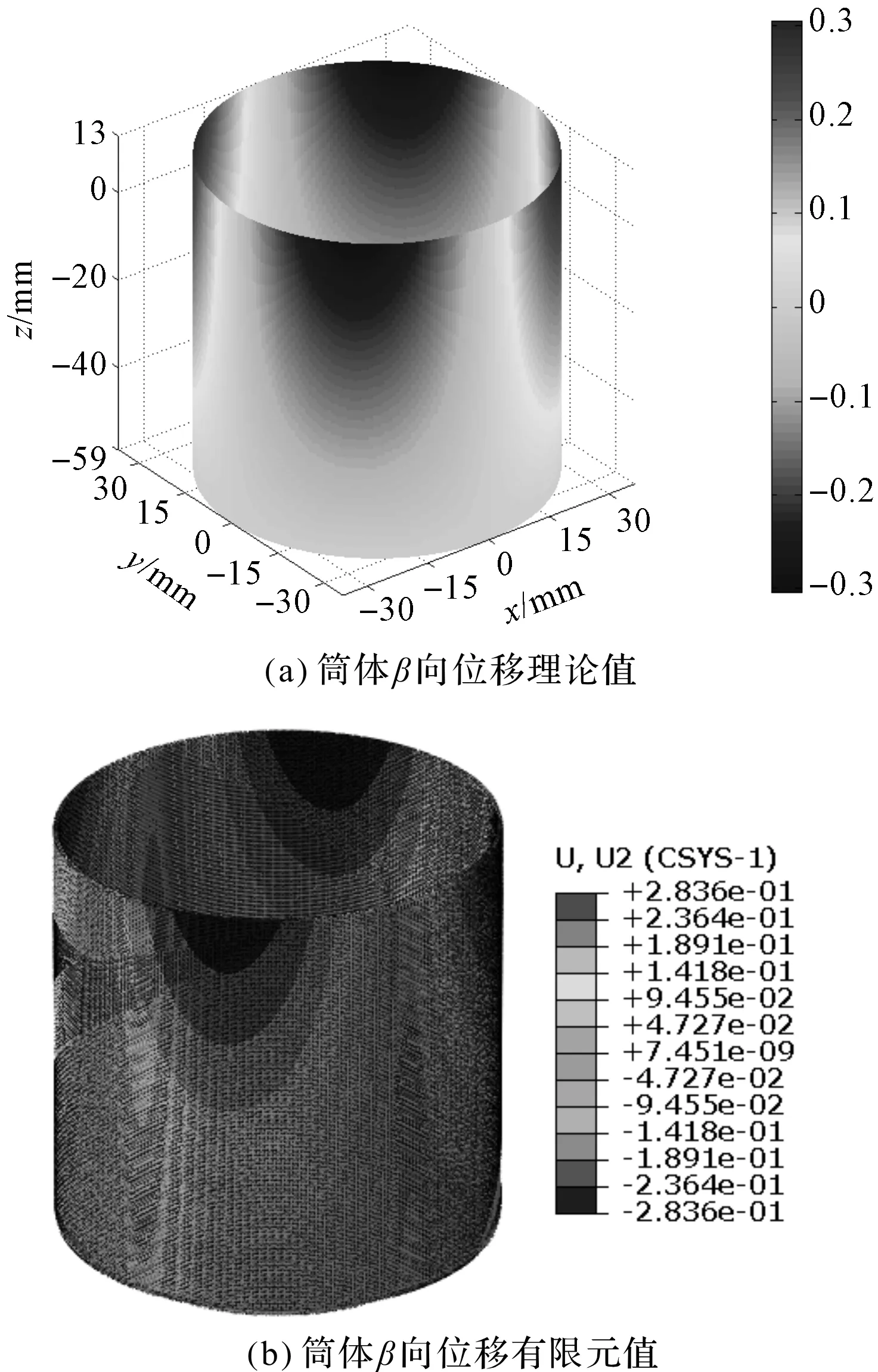
图6 柔轮筒体β向位移
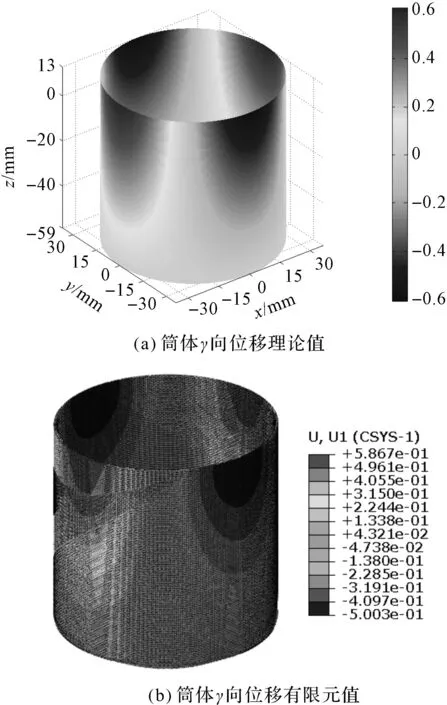
图7 柔轮筒体γ向位移
通过观察图(5~7)可以发现:理论计算出的各方向位移和有限元结果的分布基本完全一致;其中,理论计算的α、β、γ3个方向的中面位移,最大值分别为0.076 mm,0.30 mm,0.60 mm,有限元得到的最大值分别为0.072 mm,0.28 mm,0.58 mm。
由此可以说明本文的计算方法能够有效、准确地计算出柔轮筒体上各位点的位移。
4 结束语
本文对柔轮的受力模型情况进行了简化,用一圈径向线载荷等效波发生器对柔轮筒体的作用力;在此基础上提出了一种考虑轴向变形的柔轮中面各点位移的计算方法。
由该方法得到的理论值与有限元值的最大误差为6.7%,且很好地体现了柔轮轴向变形带来的影响,更加符合实际变形结果。
本文的计算模型适用于各种边界条件下的谐波减速器柔轮;同时,利用本文的结果,可以进一步算出柔轮筒体上各点的总位移及其各向应力大小,从而更加高效、准确地进行柔轮筒体的强度校核与优化设计。
