地基不均匀沉降下大型储罐变形规律和预测方法研究*

陈严飞 马尚 董绍华 娄方宇 孙文勇 赵永涛 孙秉才 倪恒

1中国石油大学（北京）油气管道输送安全国家工程实验室·石油工程教育部重点实验室·城市油气输配技术北京市重点实验室2大连理工大学工业装备结构分析国家重点实验室3中国石油集团安全环保技术研究院

随着大型国家原油储备库不断兴建，原油储罐日趋大型化。大型储罐是一种典型的薄壳结构，在石油工业中被广泛应用于原油及成品油的储存，具有节约建设成本、减少占地面积、便于管理等优点。大部分储罐建在地基条件较差的沿海地区，随着服役年数的增加，储罐地基常会发生不同程度的沉降。过量的地基沉降会导致储罐上部罐壁发生较大变形，严重时会导致浮盘卡盘，影响储罐的正常运行，甚至造成储罐结构发生破坏，引发泄漏事故。因此，地基沉降条件下大型储罐的安全和完整性问题至关重要。

关于地基沉降下大型储罐安全评价，现行标准API 653—2014[1]、SH/T 3123—2017[2]、SY/T 5921—2017[3]等对储罐沉降提出了不同的控制要求。评价指标主要有对径点沉降差、相邻点沉降差、不均匀沉降等，但标准尚未统一，评价结果也不尽相同。近年来，国内外学者从能直接反映沉降下储罐变形情况且便于测量的储罐径向位移入手进行研究，通过探索变化规律和拟合公式对储罐沉降安全评价提出建议。陈冰冰等[4]采用千分表和应变计，实验测量了锥壳圆筒过渡段在内部升压过程中的应变及径向位移变化，总结了内压下薄壁锥壳圆筒过渡段变形特征，为锥壳变形控制准则研究打下基础。蒋鹏程等[5]通过测试充水过程中罐壁应力的变化开展罐壁静态应力的试验研究，证实罐壁上部的抗风圈和加强圈对罐壁径向位移的控制作用。陈志平等[6]依据弹性板壳理论，对设置了加强圈的储罐变形进行力学分析，建立起加强圈设置高度和横截面积大小与罐壁径向位移间的关系；同时，利用该解析解研究不同加强圈横截面积和设置高度对油罐壁板危险区域的环向薄膜内力分布和径向位移的影响。杨志波等[7]开展储罐在充液静压力作用下的静力分析，得到半罐、满罐罐壁径向位移和等效应力的分布及变化规律。MALIK 等[8]、D'ORAZIO 等[9]、KAMYAB等[10]、GODOY等[11]、曹庆帅[12]等学者都对储罐径向位移进行了研究，提出或修正了相应准则。但大多数学者在研究时忽略了储罐几何参数对不均匀沉降下储罐结构响应的影响。而研究表明，储罐几何参数与储罐结构响应密切相关，如果对此考虑不足，将导致公式准则适用性变差，从而降低完整性评价方法的可靠性。为了解决上述问题，本文通过建立变参数大型储罐有限元模型，开展不同敏感参数对地基沉降下储罐罐顶变形影响的研究，提出一种地基沉降条件下等壁厚储罐罐顶径向位移计算方法，可为不均匀沉降下大型储罐完整性评价提供参考。

1 理论基础

1.1 傅里叶分解

目前广泛采用傅里叶分解对储罐基础实测沉降数据进行处理，再将处理结果应用于后续研究。在实际沉降观测中，由布置在罐周基础外侧的若干个水准观测点测量获得的罐周实测沉降离散数据，仅能部分反映储罐基础的沉降情况，而过多设置水准观测点又不具有经济性和实用性。在获得有限个储罐基础实测沉降数据的基础上，MARR、KAMYAB等[13-14]建议采用傅里叶分解方法对其进行处理，可得到罐周任意一点的近似沉降值和形式简洁的各阶谐波沉降形式。罐周沉降对储罐结构的影响十分复杂，而对实测沉降进行傅里叶分解后，既可直接研究组合谐波沉降对储罐的影响，也可先分别研究各阶谐波沉降单独作用时对储罐的影响，再将得到的结果进行线性叠加，获得完整的储罐结构响应。把罐周的实际沉降量u用傅里叶级数进行展开（式1）。

式中：u0为储罐的整体均匀沉降量，mm；un为各阶谐波沉降的幅值，mm；n为谐波沉降的阶数；φ为罐周各点所处的角度，rad；φn为各阶谐波沉降的初始相位角，rad。

选取某实际储罐沉降值，对其进行傅里叶分解得到各阶谐波沉降幅值和初始相位角（表1），后续作为边界条件施加在有限元模型上。

表1 实测沉降傅里叶分解结果Tab.1 Fourier decomposition results of measured settlement

1.2 公式理论解

利用薄膜公式与修正Donnell 公式可推导出等壁厚储罐罐顶径向位移公式（式2、式3）。曹庆帅提出了谐波沉降条件下等壁厚储罐罐顶最大无量纲径向位移的拟合公式（式4）。

式中：[w]x=h为高度h处罐壁径向位移，mm；h为储罐高度，mm；θ为壳体上任一点环向坐标分量，rad；ν为泊松比；r为储罐半径，mm；IG为抗风环梁的周向变曲刚度，mm4；t为储罐罐壁厚度，mm；Iratio为无量钢参数；wn为n阶谐波下罐顶最大径向位移，mm；

对该储罐有限元模型分别施加2～12 阶谐波沉降，计算得到罐顶最大无量纲径向位移，并与薄膜理论解、修正Donnell 公式解及曹庆帅提出的拟合公式结果进行对比（图1）。薄膜理论解仅考虑了壳体的薄膜效应，未考虑壳体的弯曲效应，修正Donnell 公式解则将这两种效应都考虑在内。因此，在谐波阶数较小、壳体弯曲效应表现不明显时，两种理论解差距很小；而在谐波阶数较大、壳体弯曲效应显著时，仅有Donnell 公式解能够真实反映实际情况，薄膜理论解不再适用。学者研究分析表明，储罐在不均匀沉降下的结构响应与其几何参数密切相关[15]，因此，利用薄膜公式与修正Donnell公式推导等壁厚储罐罐顶径向位移公式从结构角度看不尽合理。曹庆帅提出的拟合公式考虑了储罐几何参数，但与两种理论解及有限元计算结果相差较大。其在进行参数敏感性分析时，选择的抗风环梁相对刚度范围为5～60，无法确认该拟合公式在其他条件下的适用性。针对上述情况，需提出一种适用性更好的考虑储罐几何参数的等壁厚储罐罐顶径向位移计算公式。

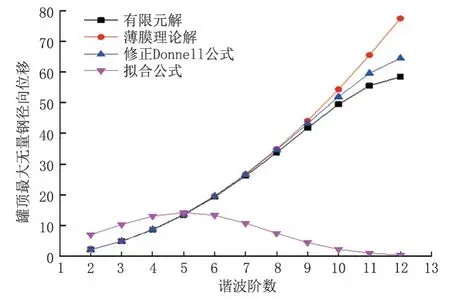
图1 各公式结果及有限元结果对比Fig.1 Comparison of various formula results and finite element results

2 有限元模型

采用我国某10×104m3大型外浮顶储罐的结构数据进行储罐有限元模型建立（图2）。所选储罐直径为80 m，高度为21.7 m，底板的直径为80.4 m，厚度为20 mm。在储罐罐壁顶部设有包边角钢，尺寸为100 mm×12 mm。建立模型时考虑抗风圈、加强圈（图3）。假定储罐所用板材材料为钢，材料参数为：弹性模量E=2.06×1011Pa，泊松比ν=0.3。有限元模型的边界条件为：储罐为空罐；约束储罐底板的径向位移及切向位移，防止储罐发生刚体运动；地基沉降通过在储罐底板底部施加竖向位移进行模拟，储罐底板最外侧沉降量为处理得到的地基沉降；底板中心点的沉降取最外侧沉降的平均值，其余各点的沉降沿半径方向呈线性变化；模型其余各处均为自由边界。

图2 储罐有限元模型Fig.2 Storage tank finite element model

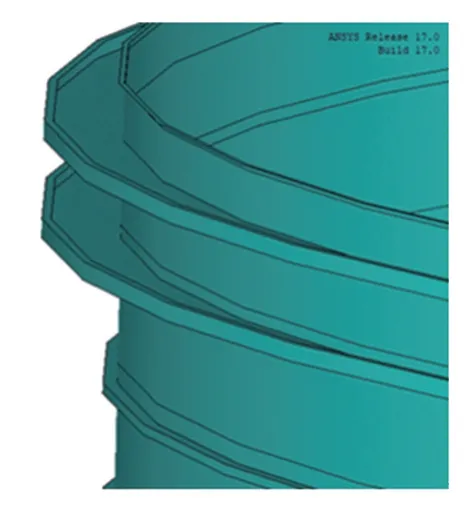
图3 抗风圈、加强圈结构Fig.3 Structure of wind girder and reinforced ring

为确保计算结果准确性，进行模型正确性验证。自行设计搭建小型地基沉降储罐模型实验装置1套（图4），利用升降杆组拉动刚性支撑平台模拟实际不均匀沉降对储罐罐壁的影响。储罐模型直径为610 mm，高为150 mm，罐壁厚度为0.25 mm，储罐材料为 304 不锈钢，弹性模量E=1.95×1011Pa，泊松比ν=0.3。建立与实验装置一致的有限元模型。采用实验时施加的底部位移作为储罐有限元模型的边界条件并进行计算分析，将有限元计算结果与实验结果进行对比（表2），有限元计算结果与实验结果相对误差均小于10%。

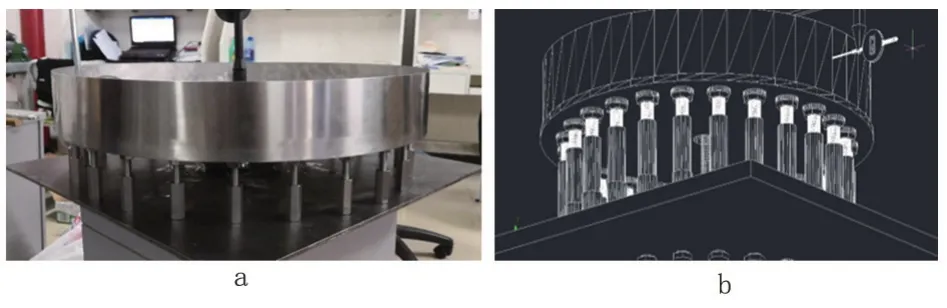
图4 地基沉降储罐模型实验装置Fig.4 Experimental device of foundation settlement storage tank model

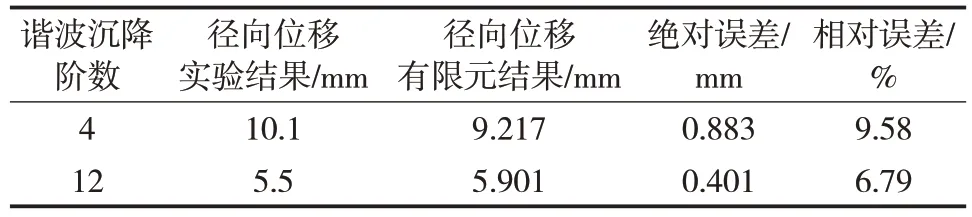
表2 有限元结果与以底部位移作为边界条件的实验结果对比Tab.2 Comparison between finite element results and experimental results taking bottom displacement as the boundary condition

MALIK 等也曾在其研究中搭建过小型地基沉降储罐模型实验装置，该装置中的储罐模型与所建储罐有限元模型结构一致但尺寸不同。采用MALIK等实验时施加的沉降作为储罐有限元模型的边界条件并进行计算分析，将有限元计算结果与实验结果进行对比（表3），有限元计算结果与实验结果相对误差均小于10%。综上所述，储罐有限元模型可用于后续径向位移的分析计算及研究。

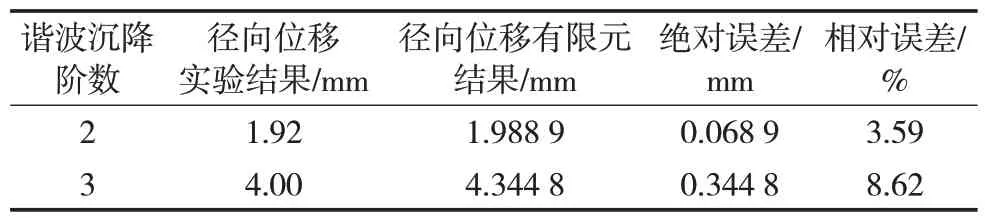
表3 有限元结果与以沉降作为边界条件的实验结果对比Tab.3 Comparation between finite element results and experimental results taking settlement as the boundary conditon

3 参数敏感性分析

3.1 高径比

在保持径厚比与抗风环梁相对刚度不变的基础上改变储罐的高径比，分别计算各阶谐波沉降条件下等壁厚储罐的罐顶最大无量纲径向位移（图5）。在同一高径比下，当谐波阶数在一定范围内时，储罐承受阶数越高的谐波沉降，越容易产生较大的罐顶径向位移；当谐波阶数进一步增大时，储罐对谐波沉降的敏感性开始下降。高径比较大储罐对6～8 阶谐波沉降更为敏感，承受6～8 阶谐波沉降时更易产生较大的罐顶径向位移；而高径比较小储罐则对10～12 阶谐波沉降更为敏感，承受10～12 阶谐波沉降时更易产生较大的罐顶径向位移。

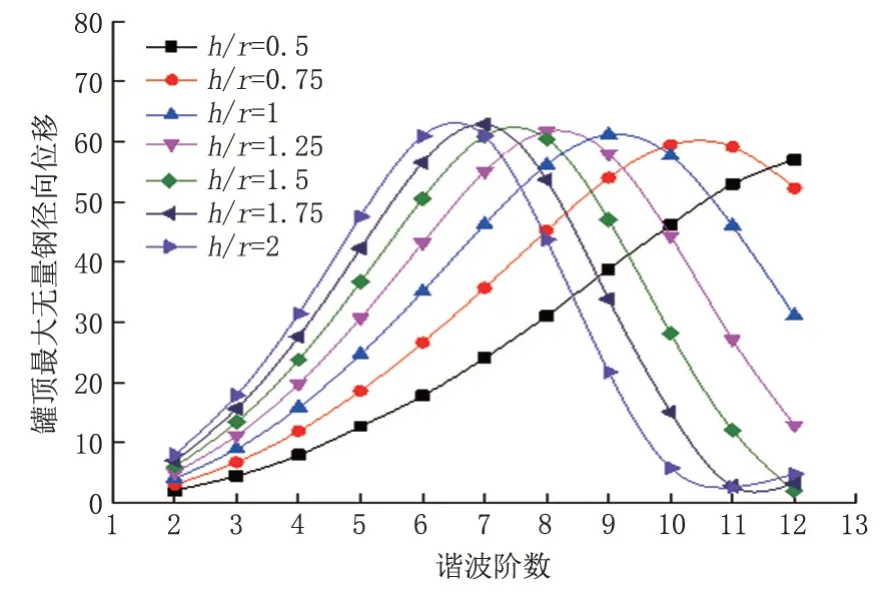
图5 不同高径比下罐顶最大无量纲径向位移Fig.5 Maximum dimensionless radial displacement of tank top under different height-diameter ratios

3.2 径厚比

在保持高径比与抗风环梁相对刚度不变的基础上改变储罐的径厚比，分别计算各阶谐波沉降条件下等壁厚储罐的罐顶最大无量纲径向位移（图6）。在同一径厚比下，当储罐径厚比较小时，罐顶最大无量纲径向位移存在极大值；而当储罐径厚比较大时，谐波沉降阶数对罐顶变形的影响变为单调递增关系，谐波沉降的阶数越高，对罐顶变形的影响越大。储罐径厚比会在一定程度上影响储罐对谐波沉降的敏感程度，径厚比较小储罐对9～11 阶谐波沉降更为敏感，承受9～11 阶谐波沉降时更易产生较大的罐顶径向位移；而径厚比较大储罐对12 阶谐波沉降更为敏感，并且此特性不再随径厚比的改变而变化。

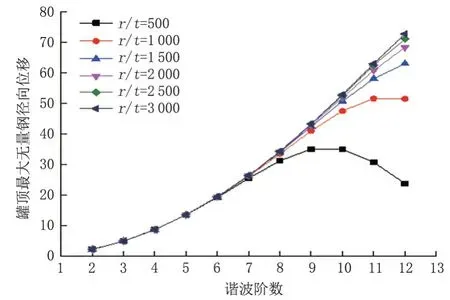
图6 不同径厚比下罐顶最大无量纲径向位移Fig.6 Maximum dimensionless radial displacement of tank top under different diameter-thickness ratios

3.3 抗风环梁相对刚度

在保持高径比与径厚比不变的基础上改变储罐的抗风环梁相对刚度，分别计算各阶谐波沉降条件下等壁厚储罐的罐顶最大无量纲径向位移（图7）。在同一抗风环梁相对刚度下，当谐波阶数在一定范围内时，储罐承受的谐波沉降阶数越高，越容易产生较大的罐顶径向位移；而当谐波阶数进一步增大时，储罐对谐波沉降的敏感性开始下降，不同抗风环梁相对刚度的储罐对谐波沉降阶数的敏感程度是不一样的，但总体上都对较高阶数的谐波沉降更为敏感。随着储罐抗风环梁相对刚度的增大，罐顶最大无量纲径向位移都单调递减，即谐波沉降条件下抗风环梁相对刚度较大的储罐抵抗罐顶变形的能力较强。

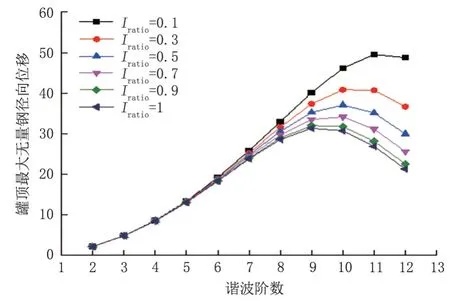
图7 不同抗风环梁相对刚度下罐顶最大无量纲径向位移Fig.7 Maximum dimensionless radial displacement of tank top under relative stiffness of different wind resistant ring beams

4 罐顶最大径向位移计算方法

由图5 至图7 可知，高径比、径厚比、储罐抗风环梁相对刚度对谐波沉降条件下储罐罐顶变形具有显著影响。在提出地基沉降条件下等壁厚储罐罐顶径向位移计算方法时，需将高径比、径厚比、储罐抗风环梁相对刚度皆考虑在内，以保证计算方法的可靠性。回归得到谐波沉降条件下等壁厚储罐罐顶最大无量纲径向位移拟合公式（式5）。

将不同情况下该拟合公式计算得出的罐顶最大无量纲径向位移与有限元结果进行对比（图8），可以看出拟合公式计算结果与有限元结果吻合较好。

将式（5）进行变换可得到谐波沉降条件下等壁厚储罐罐顶径向位移公式（6）。

将各阶谐波沉降作用下的罐顶径向位移公式叠加，即可得到沉降作用下罐顶任意位置径向位移预测值式（7）。

式中：w为实际沉降作用下的罐顶任意位置径向位移预测值，mm；N为储罐沉降周边测点个数。

5 结论

储罐地基不均匀沉降会影响储罐安全运行。通过建立大型储罐数值仿真模型，研究了储罐高径比、径厚比、抗风环梁相对刚度等参数对储罐结构变形的影响规律，提出了不均匀沉降下大型储罐罐顶径向位移预测方法，并由此得出以下结论：

（1）数值仿真计算结果与模型实验结果吻合较好，表明数值仿真是不均匀储罐地基沉降罐壁变形计算的可靠手段。

（2）在同一高径比下，罐顶径向位移随谐波阶数的增大而先增大后减小。在同一径厚比下，径厚比较小时罐顶最大无量纲径向位移存在极大值；当径厚比较大时，谐波沉降阶数对罐顶变形的影响变为单调递增关系。在同一抗风环梁相对刚度下，罐顶径向位移随谐波阶数的增大而先增大后减小。

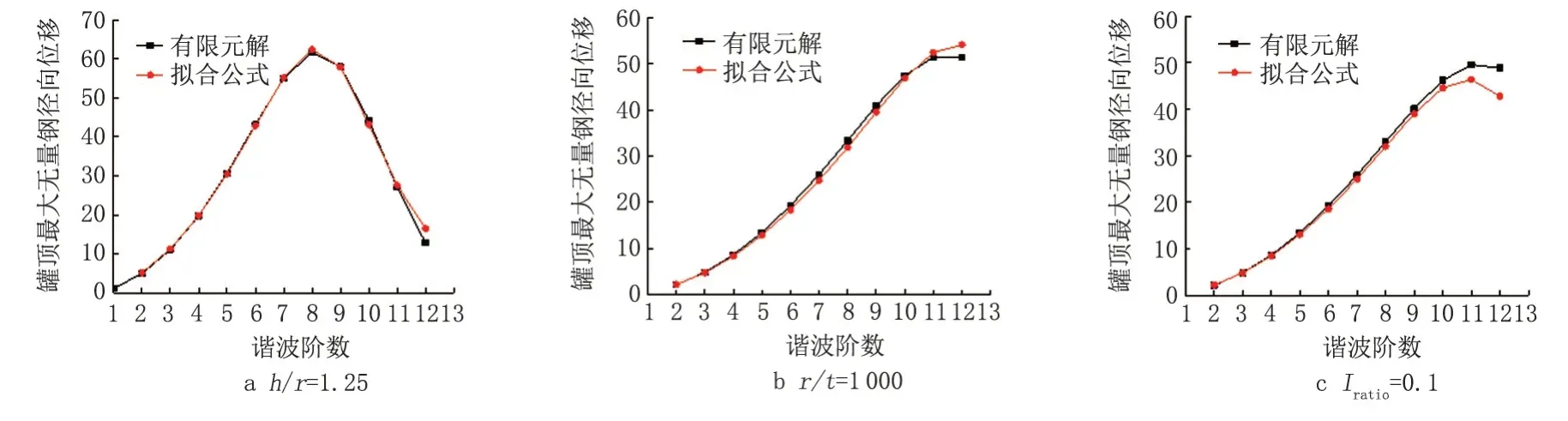
图8 预测方法与有限元结果对比Fig.8 Comparison of prediction methods and finite element results

（3）高径比、径厚比、储罐抗风环梁相对刚度等敏感参数对谐波沉降条件下储罐罐顶变形具有显著影响，提出地基沉降条件下大型储罐罐顶径向位移预测方法，综合考虑了高径比、径厚比、储罐抗风环梁相对刚度等参数的影响。

（4）经对比，本文提出的综合考虑储罐高径比、径厚比及抗风环梁相对刚度等参数的罐顶位移预测方法，可以得到较为准确的结果，为地基不均匀沉降下大型储罐完整性评价提供参考。