关联余割函数的Hilbert 型不等式及其应用

有名辉，范献胜

（浙江机电职业技术学院 数学教研室，浙江杭州310053）

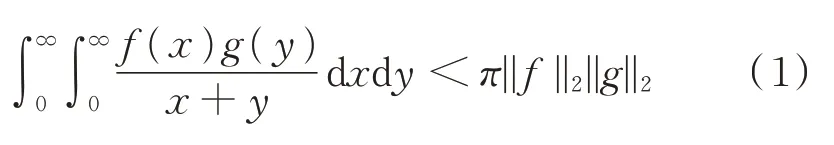
以及

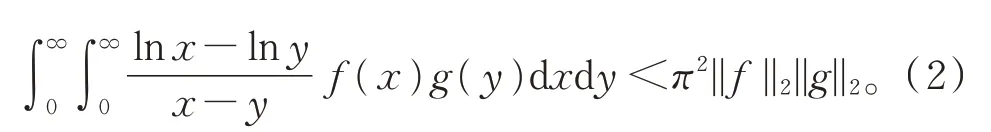
其 中，f(x)，g(y) ≥0，f(x)，g(y) ∈L2(R+)，且π和π2分别是式（1）和式（2）的最佳常数因子。

近年来，Hilbert 型不等式一直是较热门的研究课题。研究者通过引入参数和特殊函数，构造新的核函数，并考虑积分型、离散型、半离散型、齐次型、非齐次型、高维推广、系数加强以及算子表示，构造了大量类似于式（1）和式（2）的新成果［3-11］。这些新成果相互交融，已然形成了一个庞大的理论体系，对分析学的发展和应用起到了重要的促进作用［12］。

易见，核函数非负是研究Hilbert 型不等式的必要条件，而在核函数构造过程中，可能会遇到不恒正因子。为保证核函数为正，一种方式是把两个同号因子相乘，例如式（2）中给出的积分核函数(lnx−lny)(x−y)−1；另一种方式是对负因子加绝对值，如文献［4］中建立的以|x−y|−λ和

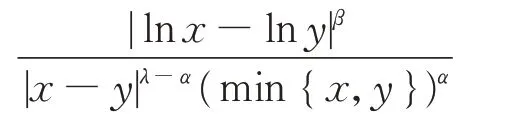
为核函数的Hilbert 型不等式。本文采用第一种方式，构造核函数

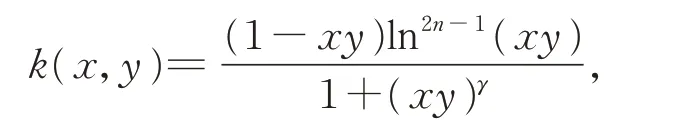
建立相关的Hilbert 型不等式，并通过对参数赋值，得到一些新的有趣的推论。

1 引 理

引 理1设c1，c2＞0，且c1+c2=c，n∈N+，φ(x)=cscx，则

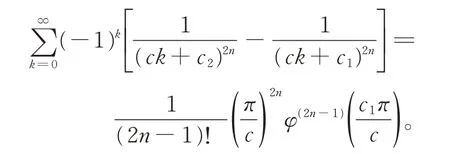
证明利用φ(x)=cscx的部分分式展开（见文献［13］），有

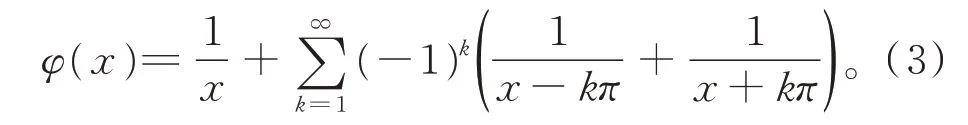
式（3）两边关于x逐项求2n−1 阶导数，得

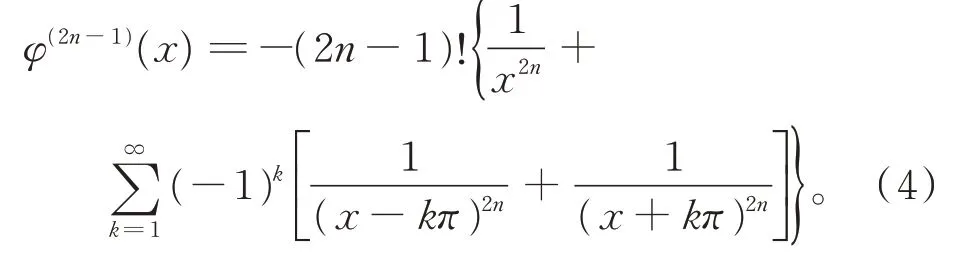
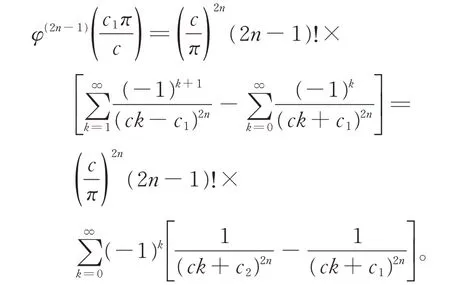
证毕。

引 理2设γ＞1，−1＜β＜γ−2，n∈N+，φ(x)=cscx，且

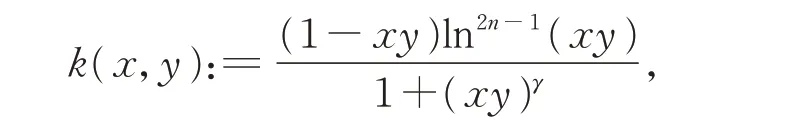
则有

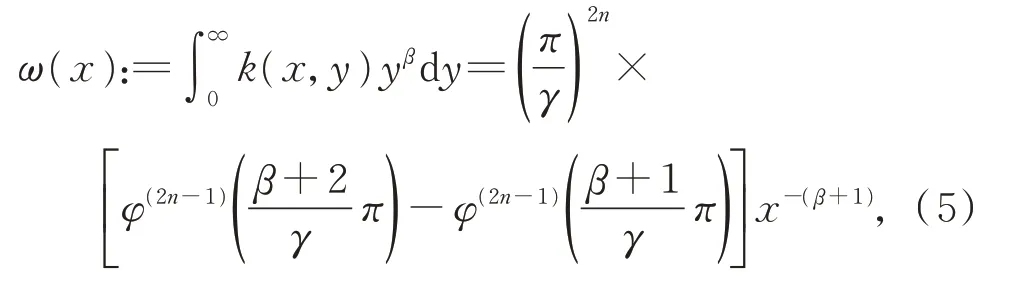
且有

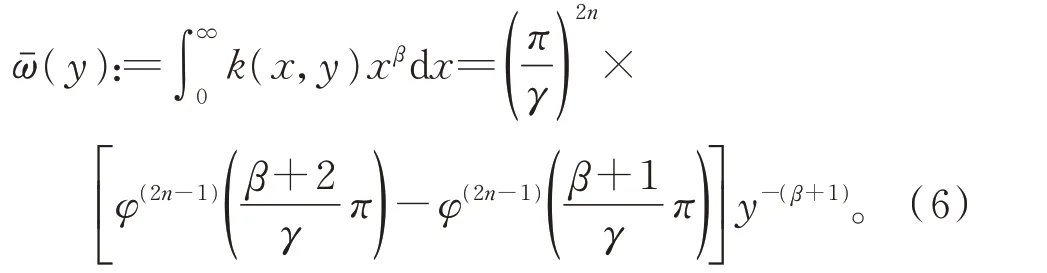
证明令xy=t，则

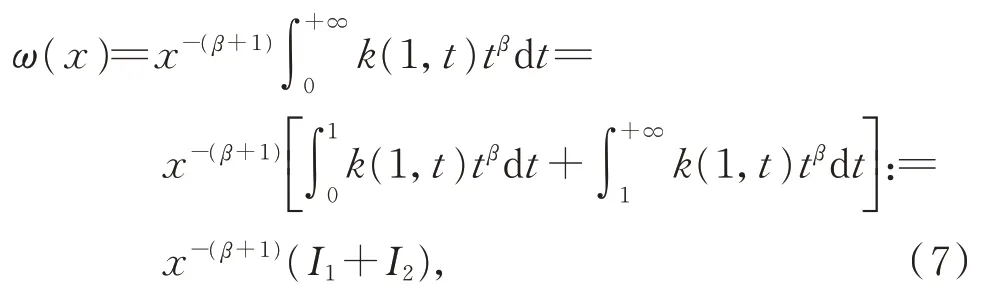
而

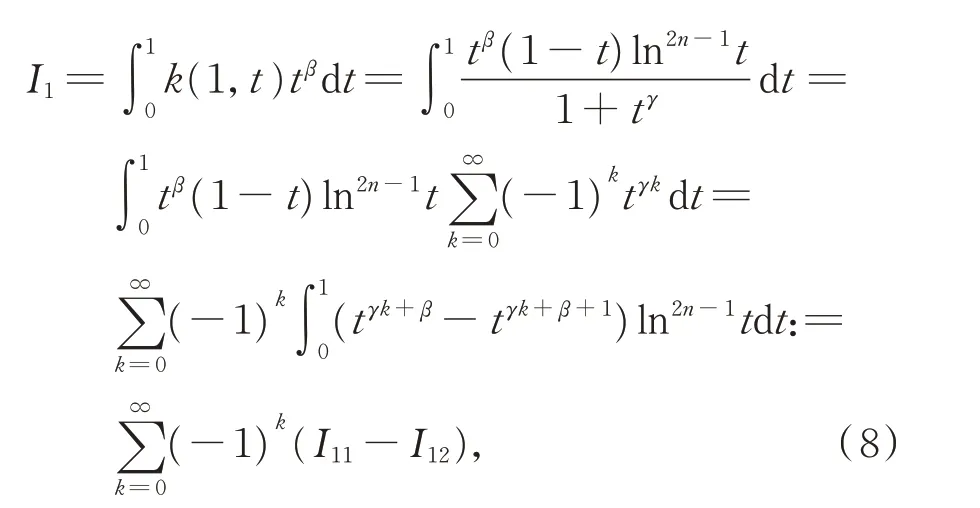
令lnt=，得

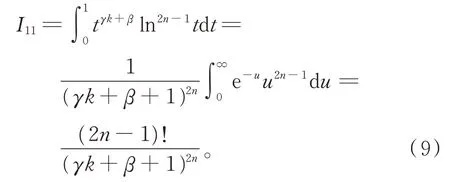
类似地，有

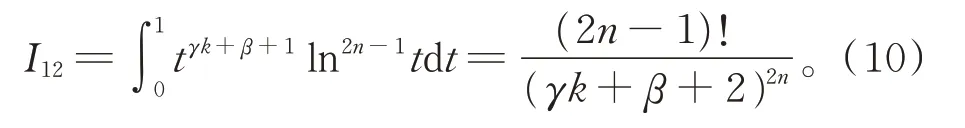
由式（8）～式（10），有

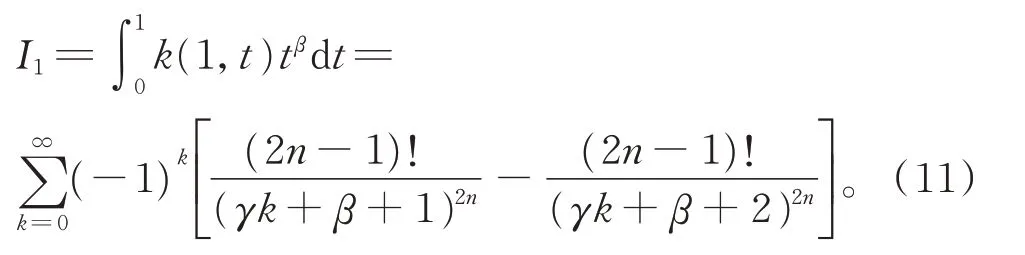
类似可得

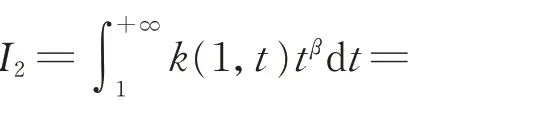
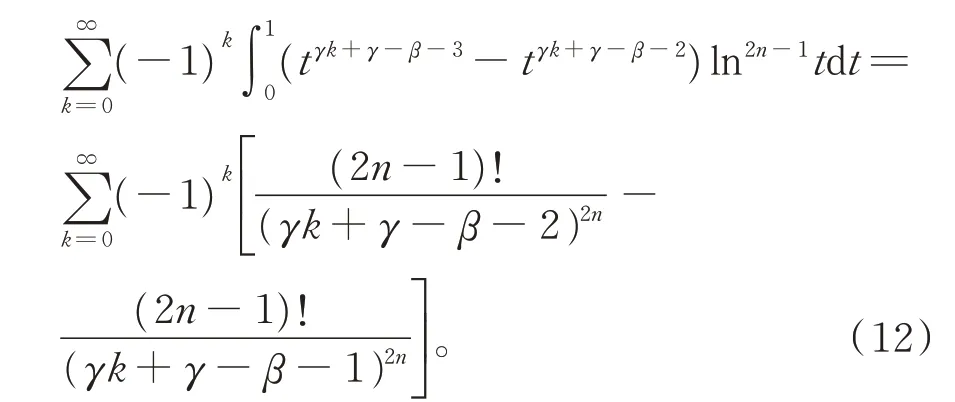
注 意 到，β+1+(γ−β−1) =β+2+(γ−β−2)=γ，结合式（11）和式（12），由引理1，可得

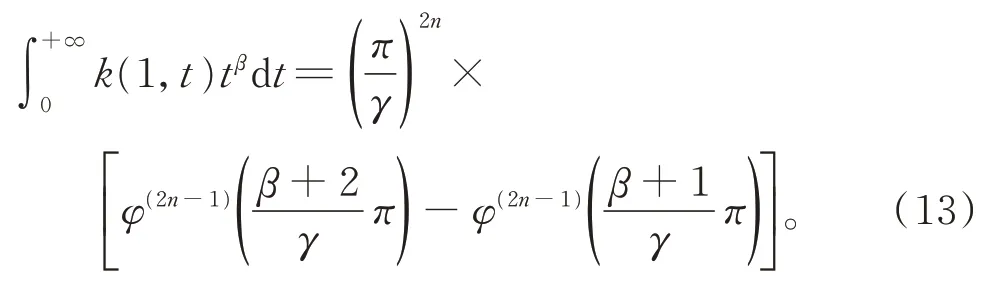
由式（7）和式（13），可得式（5）。同理可得式（6）。证毕。

2 主要结果

定 理1设γ＞1，−1＜β＜γ−2，n∈N+，φ(x)=cscx，k(x，y) 如 引 理 2 定 义，μ(x)=x−(pβ+1)，ν(x)=x−(qβ+1)，且 有f(x)，g(y)≥0，则

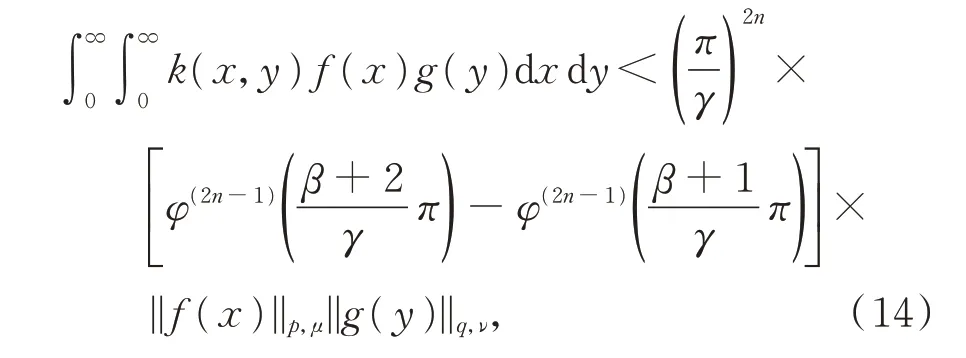
证明由Hölder 不等式［14］及引理2，知

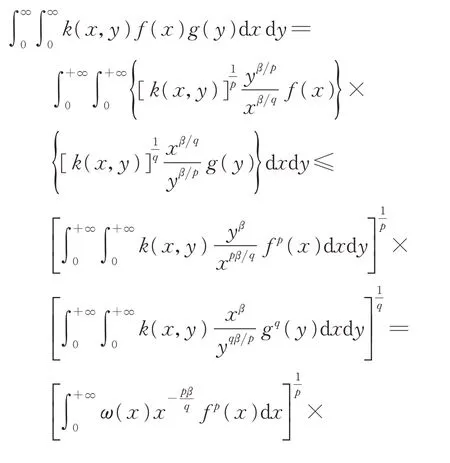
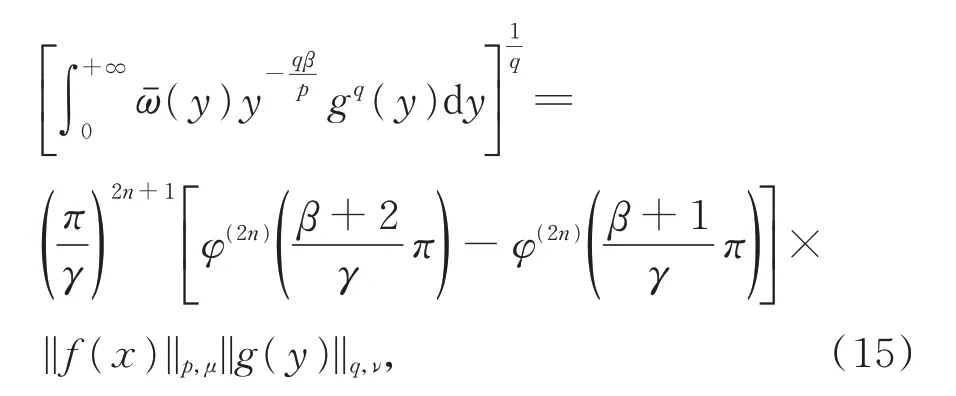
如果式（15）成立，则必存在不全为零的数A1和A2，使得

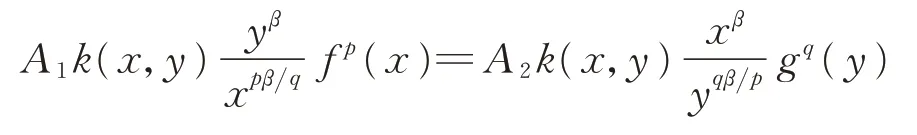
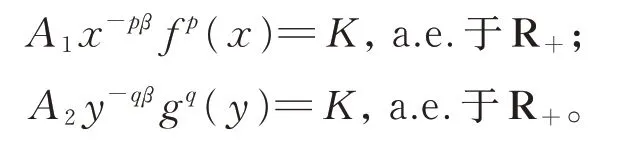
不 妨 设A1≠0，则a.e.于R+，显然与条件矛盾。所以，式（15）取严格不等号。

最后，用反证法证明式（14）中的常数因子为最佳因子。

事实上，若此常数因子不为最佳，则存在更小实数C，

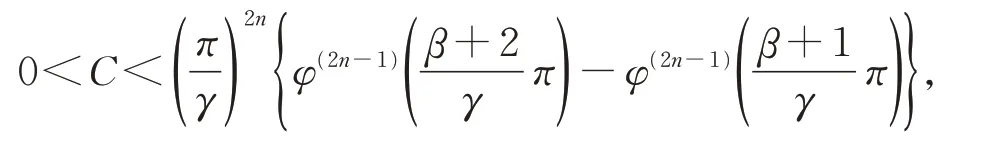
将式（14）中的常数因子换成C后，式（14）仍然成立，即

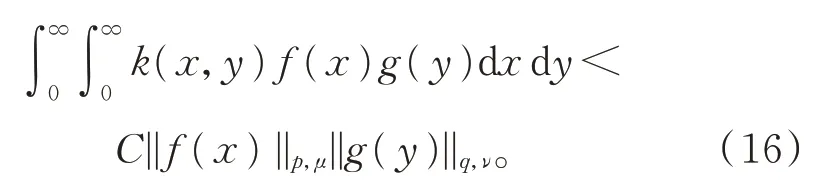
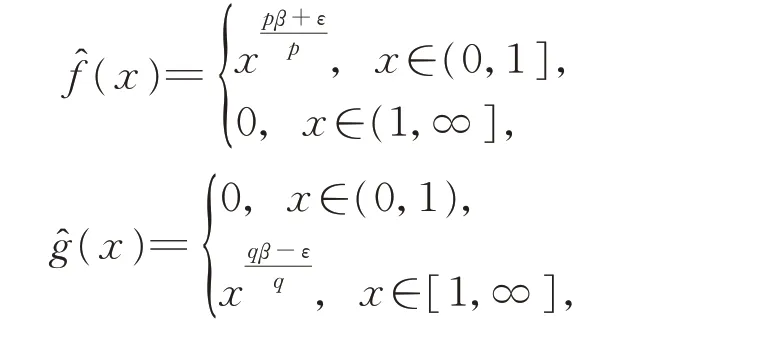
令xy=u，由Fubini 定理，知

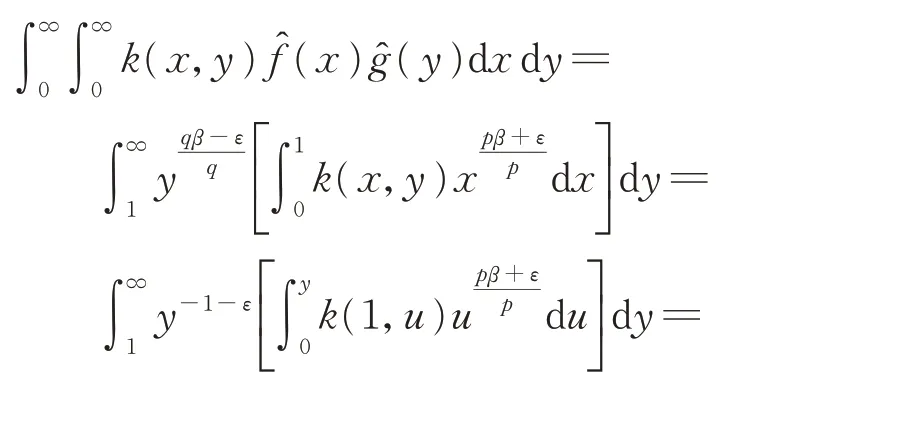
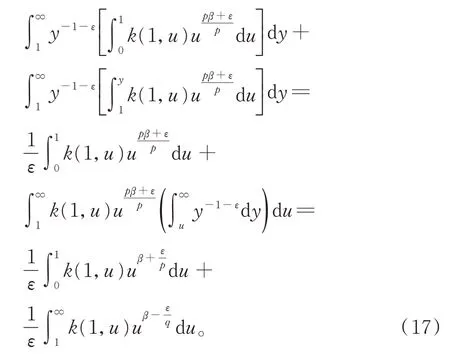
用f(x)和g(y)分别替代式（17）中的由式（16），不难得到

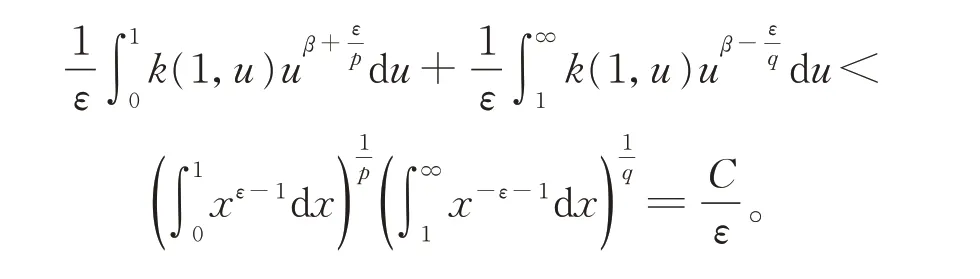
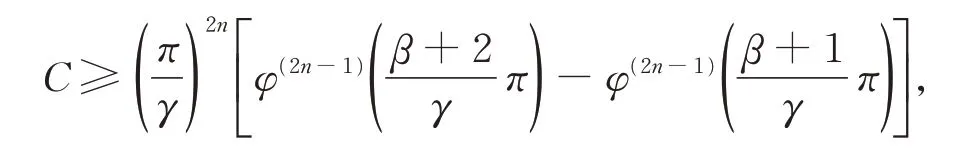
证毕。

推 论 1设γ＞1，n∈N+，φ(x)=cscx，则

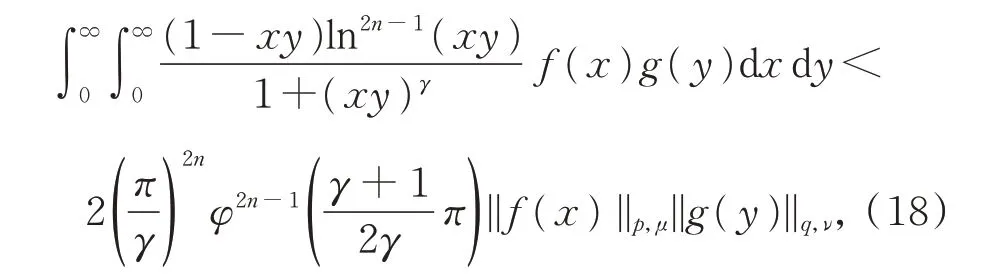
其中，令γ=2，n=1，则此时，式（18）化为

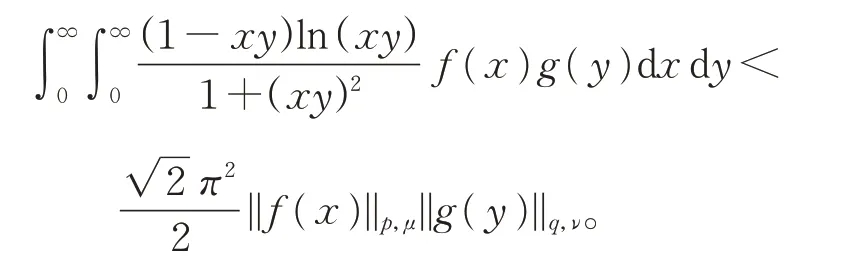
推论2设γ＞2，n∈N+，φ(x)=cscx，μ(x)=则

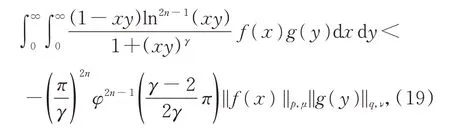
其中，令γ=3，n=1，则此时，式（19）化为