基于拉伸特征的B-Rep→CSG 转换算法及其应用

罗月童，韩承村，杜华，严伊蔓

（1.合肥工业大学计算机与信息学院，安徽合肥 230601； 2.中国科学院 等离子体物理研究所，安徽合肥 230031； 3.国家电投集团科学技术研究院有限公司，北京 100033）

0 引 言

边界表示（boundary representation，B-Rep）法和构造实体几何（construction solid geometry，CSG）法是使用最广泛的2 种实体表示法，其中B-Rep 法已广泛应用于各种商用CAD 软件，借助商用CAD软件强大的造型功能，用户能方便快捷地构建三维B-Rep 模型。也有很多科学计算程序用CSG 法，如粒子输运程序MCNP［1］、cosRMC［2］等，这是因为CSG 法具有对科学计算程序非常重要的稳定、简单等优点。目前市场上能直接构建CSG 模型的成熟软件较少，因此希望借助商业CAD 软件建立B-Rep模型，然后将B-Rep 模型自动转换为CSG 模型，以减轻建模工作量。如面向MCNP、cosRMC 等粒子输 运 程 序 的cosVMPT［3］、MCAM［4］、McCAD［5］等软件，这些软件的核心功能都是将B-Rep 模型转换为CSG 模型，即B-Rep→CSG 转换算法。本文源于自主研发的粒子输运COSINE 可视建模（COSINE visual modelling of particle transport，cosVMPT）软件，旨在基于拉伸特征提升B-Rep→CSG 转换算法的稳定性和速度，以提高cosVMPT 软件对大规模模型的处理能力。

B-Rep→CSG 转换问题备受关注［6］，主要有三类转换方法：（1）半空间分割法［7］，通常利用某些面分割B-Rep 模型，基于面的半空间分割组合获得CSG 表示，其核心是分割面的选择，较常见的做法是从B-Rep 模型中提取分割面。文献［8-9］利用CLoop 环构造分割面以改善分割效果，但CLoop 环的识别比较复杂。（2）交替和差分解法［10］，通过求BRep 模型的凸包并与之做布尔减运算得到差体，继续对差体求凸包并与之做布尔差运算，如此反复循环直至差体为空，将凸包和差体组合得到B-Rep 模型的CSG 表示。（3）单元分解法［11-12］，将B-Rep 模型分解为一组单元体，用优化方法求解相关单元体组合，实现B-Rep→CSG 转换，但此类方法通常存在过分割问题。半空间分割法因其具有直观、易实现等优点广受关注，其中，cosVMPT、MCAM、McCAD 采用的均为半空间分割法。

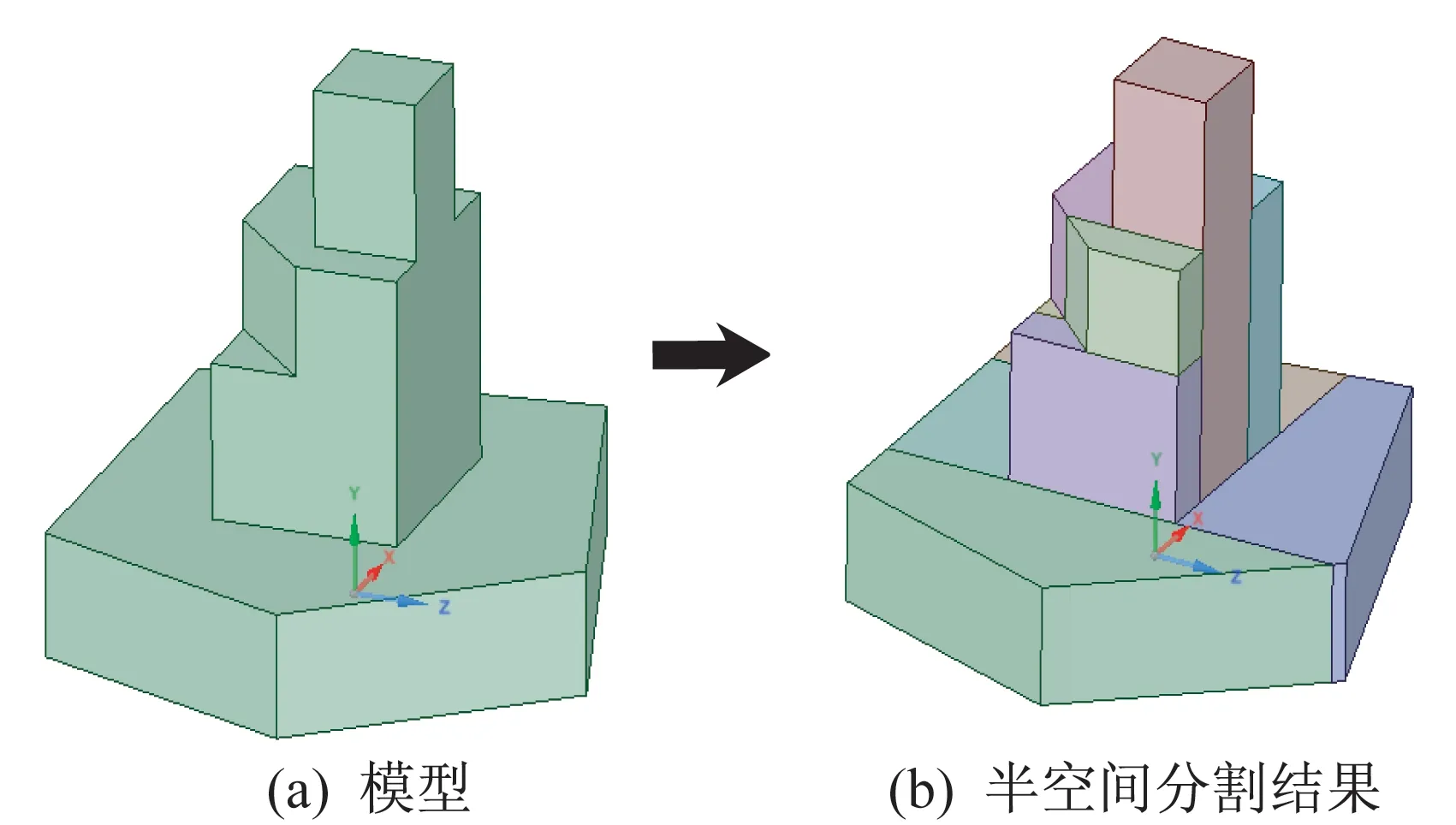
图1 半空间分割法示意图Fig.1 Schematic diagram of half space partition method

半空间分割法，沿一系列面将B-Rep 模型分解为若干简单模型，然后基于简单模型实现B-Rep→CSG 转换，图1 展示的为模型的分割过程。对复杂的B-Rep 模型分割量较大，通常通过造型引擎的布尔交/减运算实现分割，如MCAM 采用商业造型引擎ACIS［13］，cosVMPT 和McCAD 采用开源造型引擎OpenCascade［14］。经过多年发展，虽然ACIS、OpenCascade 引擎已较成熟，但因为布尔运算涉及复杂的数值运算，所以仍然存在布尔运算失败的概率。 笔者在实践中发现，开源造型引擎OpenCascade 失败概率更高，从而降低了B-Rep→CSG 转换算法的稳定性。因为cosVMPT 等软件经常需要一次性转换数万个B-Rep 模型，中国聚变工程 实验堆（China fusion engineering test reactor，CFETR）模型由50 000 多个B-Rep 模型组成，如图2 所示，存在布尔运算失败导致转换失败的概率，因此，在实际应用中，不得不对模型进行预处理，如将复杂的B-Rep 模型预先分解为若干简单的B-Rep模型，这不仅需耗费大量时间，而且对用户的CAD建模技能有很高要求，严重影响cosVMPT 等软件的易用性和友好性。因此，降低B-Rep→CSG 转换算法对布尔运算的依赖性、提升B-Rep→CSG 转换算法的稳定性、改善相关软件的可用性和易用性等研究具有一定的理论意义和实用价值［15-16］。

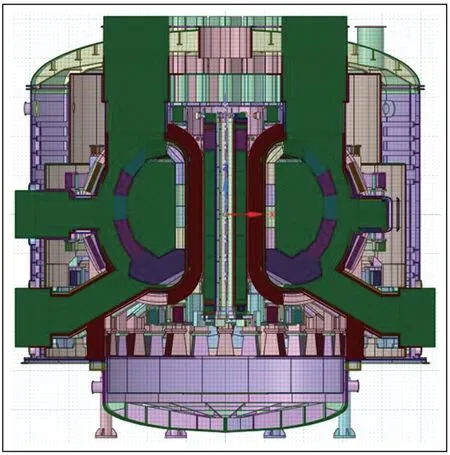
图2 CFETR 聚变堆模型Fig.2 CFETR fusion reactor model

自主研发的cosVMPT 软件常常用于处理裂变堆模型和聚变堆模型，图2 为CFETR 聚变堆模型，图3 为AP1000 裂变堆堆芯模型。笔者观察到这类模型中存在大量扫略体，即二维图形通过拉伸或旋转所形成的三维对象。基于此，提出利用扫略体特点优化B-Rep→CSG 转换：对二维图形进行B-Rep→CSG转换，然后将转换映射至三维模型。因二维图形的B-Rep→CSG 转换不需要布尔运算，通过大幅度减少布尔运算，提升B-Rep→CSG 转换算法的稳定性。扫略体通常包括拉伸体和旋转体，本文以拉伸体为例探讨优化B-Rep→CSG 转换算法。拉伸特征是指单独存在的完整拉伸体、部分拉伸体，或作为模型一部分的完整拉伸体、部分拉伸体，图4 给出了典型拉伸特征的各种存在形式，转换流程的关键是拉伸特征的识别和二维图形的B-Rep→CSG转换。

本文的主要贡献包括：

（1）提出了基于拉伸特征的B-Rep→CSG 转换算法，以减少转换算法对布尔运算的依赖，提升了算法的稳定性；

（2）给出了拉伸特征的定义及其识别方法，解决了基于拉伸特征的B-Rep→CSG 转换算法的关键问题；

（3）将所提算法集成至自主研发的cosVMPT软件，并投入实际应用。

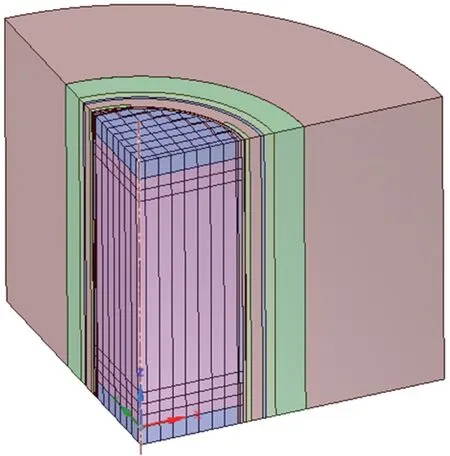
图3 AP1000 裂变堆堆芯模型Fig.3 AP1000 fission core model

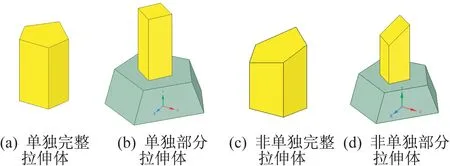
图4 拉伸特征的各种存在形式Fig.4 Various existing forms of stretch feature

1 拉伸特征的识别

由图4 可知，拉伸特征可看作由二维图形沿一定方向拉伸形成的三维图形（本文称其为拉伸体）或其一部分。其中，由二维图形的边拉伸形成的面称为拉伸面，由二维图形的顶点拉伸形成的边称为拉伸边，且所有拉伸边均为直线，如图5（a）所示。

虽然拉伸特征可能是拉伸体的一部分，但本文要求保留拉伸体所有拉伸边的全部或部分。图5（b）中，因为拉伸边被完全切割，所以其为无效拉伸体。拉伸特征包含相应拉伸体的所有拉伸边，可通过拉伸边识别拉伸特征，其核心是提取拉伸特征所包含的一组拉伸边，本文称其为拉伸边集。

图5 拉伸体、拉伸面、拉伸边示意Fig.5 Schematic diagram of extruded body，extruded surface and extruded edge

1.1 拉伸边集特点分析

为准确识别拉伸边集，笔者对拉伸边集进行了观察、分析和总结，得到以下条件。

（1）相互平行性：拉伸边集中的所有边相互平行，拉伸边集由一组平行边构成。

（2）首尾相连性：如果两条边共享一个面，则称这两条边相连。拉伸边集中的任何一条边与且仅与另外两条边相连，拉伸边集中所有边将形成一个首尾相连的环。

（3）方向相反性：按顺时针或逆时针遍历所有边，按遍历顺序定义边的方向。若拉伸边集中的两条边共享一个面，则此两条边方向相反。

（4）唯一连接性：拉伸边集中最多有两条边共享一个面。由拉伸特征的定义可知，两条边共享的面为拉伸特征的侧面，只出现一次。

上述4 条均为拉伸边集的必要而非充分条件，若一组边同时满足上述条件，则构成一个拉伸边集。本文虽然未能给出严格的理论证明，但从大量的观察、实验和实际应用中已得到验证。并基于上述结论设计了拉伸边集提取算法。

对 B-Rep 模 型M=(EM，F)，其 中EM=表示模型M中所有边的集合，F={f1，f2，…，fm}表示模型M中所有面的集合。

提取拉伸边集算法：

（i）从EM中提取所有平行边组：P1，P2，…，PK。因为相互平行性是拉伸边集的必要条件，所以M的所有拉伸边集均包含P1，P2，…，PK，每个Pi可能包含0 个或多个拉伸边集。

（ii）利用拉伸边集的首尾相连性、方向相反性和唯一连接性，从平行边组Pi中提取0 个或多个拉伸边集。

因算法（i）提取平行边组的方法比较成熟，不再赘述，下文主要讨论算法（ii）。

1.2 基于平行边连接图的拉伸边集识别

因为拉伸边集的首尾相连性与图的简单回路特点非常相似，所以采用基于简单回路的算法提取拉伸边集。提出用平行边连接图G=(V，EG)刻画平行边组各元素的连接关系，并在图G=(V，EG)中由拉伸边集的方向相反性和唯一连接性准确提取拉伸边集。

平行边连接图G=(V，EG)的构造过程：

（2）如 果vi，vj∈V所 对 应 的 平 行 边满足：

则创建边(vi，vj)∈EG；

（3）将共享面f作为边(vi，vj) 的属性，即令attr（vi，vj）=f。

如图6（a）所示，B-Rep 模型垂直方向平行边P={A，B，C，D，E，F，G，H}，其中，A-B，B-C，CD，D-A，E-F，F-G，G-H，H-E，A-F，B-E，A-E和B-F共12 对平行边共享某个面，但A-E以及B-F的共享面为f1且方向相同，其对应平行边连接图如图6（c）所示，包括8 个顶点、10 条边及边的属性。

完成平行边连接图G=(V，EG)构建后，按以下步骤提取拉伸边集：

（1）基于深度优先搜索的改进算法［8］求G=(V，EG)中所有简单回路{L1，L2，…，Ln}，其中，回路Li中的节点记为{v1，v2，…，vm}，所有边记为

图6 拉伸特征及其平行边连接图Fig.6 Stretch feature and its parallel edge connection graph

上述步骤可输出0 个或多个平行边集，可以证明，所输出的每个平行边集均满足1.1 节中的4 个条件，因此均构成拉伸边集。

证明过程如下：

（1）相互平行性：因为平行边连接图的所有节点对应模型中的一组平行边，所以输出的边集为一组平行边，满足相互平行性；

（2）首尾相连性：因为这组平行边对应图中的简单回路，所以满足首尾连接性；

（3）方向相反性：由平行边连接图构建方法可知，图中边所连接的两个顶点对应的平行边方向相反，所以满足方向相反性；

（4）唯一连接性：由提取拉伸边集算法（ii），可排除不满足该条件的简单回路，因此，最终输出结果均满足唯一连接性。

图6（c）为平行边连接图，有3 个简单回路{A，B，C，D}、{A，B，E，F}和{E，F，G，H}，如 图6（d）所 示，但 由 于{A，B，E，F} 中，attr(A，F)=attr(B，E)=f1，因此将其剔除，最后只保留有效简单 回 路{A，B，C，D}和{E，F，G，H}，见 图6（e），其分别对应图6（b）中红色和黄色所示的拉伸特征。

2 基于拉伸特征的B-Rep→CSG 转换

如果B-Rep 模型M的部分或全部是一个或多个拉伸特征F1，F2，…，Fn，那么，首先将模型M分解为模型MF1，MF2，…，MFn和MR，其中，MFi表示拉伸特征Fi对应的模型，MR表示分离所有拉伸特征后的剩余部分，图7（a）模型的分解结果见图7（b）。然后对MFi和MR实施B-Rep→CSG 转换获得相应的CSG 表示CSG(MFi)和CSG(MR)，于是B-Rep 模型M的B-Rep→CSG 转换结果可表示为CSG(M) =CSG(MR)+CSG(MFi)。

图7 拉伸特征分解过程示意Fig.7 Schematic diagram of feature decomposition process of stretch

剩余部分MR为一般的B-Rep 模型，因此采用文献［3］所述的B-Rep→CSG 算法。

2.1 基于环收缩的拉伸特征分离

拉伸特征是B-Rep 模型的一部分，可按各种方式与模型其余部分连接，图8（a）中，连接处只有一个平面，较简单，但图8（b）中，连接处涉及多个面，较复杂。无论连接处较简单还是较复杂，拉伸特征体MF和模型M之间的边界都只有一个环，而文献［9］提出基于环收缩的面壳封闭法，可依据环分离B-Rep 模型的多个部分，图8（c）展示的为相关例题，本文用环收缩算法分离拉伸特征。

文献［9］详细介绍了环收缩算法，笔者在前期工作中也已实现环收缩算法［17］。本节主要讨论拉伸特征体MF和模型M连接处环的提取，环提取后即可运用环收缩算法对拉伸特征体进行分类。本文称拉伸特征体MF和模型M连接处的环为分割环。

由图8 可知，拉伸特征边的分割环具有以下特点：

（1）每个拉伸特征有且仅有2 个分割环，分别在拉伸特征体的两端；

（2）分割环由拉伸面的边组成，且不包括拉伸边。

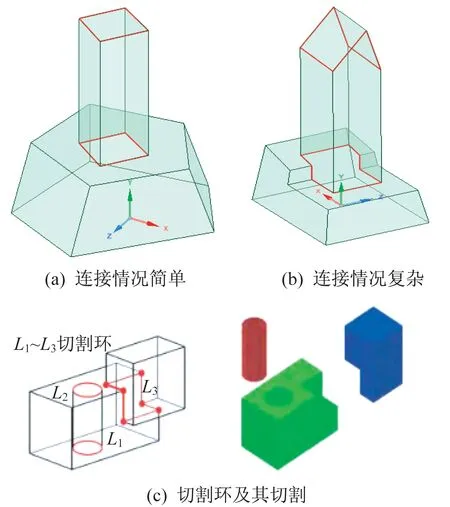
图8 切割环示意Fig.8 Schematic diagram of cutting ring

基于以上观察，对拉伸特征F，如果其拉伸边面集和边集分别为{f1，f2，…，fn}和{e1，e2，…，en}，则提取分割环的过程如下：

（1）提取所有拉伸面的边，组成集合E=其中edge(fi)表示面fi的所有边；

（2）去除所有拉伸边，形成新边集E′=E−{e1，e2，…，en}；

（3）依据E′中边的连接关系，提取分割环。

在如图9（a）所示的模型中，上面黄色部分为拉伸特征，其所对应的分割环如图9（b）所示，运用环收缩分离可获得如图9（c）所示的2 个模型。

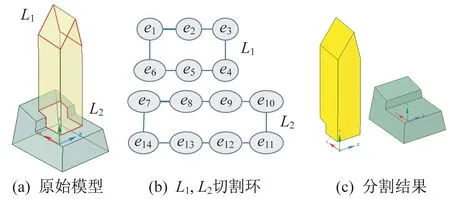
图9 基于环搜索的分割过程Fig.9 Segmentation process based on ring search

2.2 基于拉伸特征的B-Rep→CSG 转换

基于拉伸特征，将二维图形沿一定方向拉伸，将三维拉伸特征的B-Rep→CSG 问题转换为二维图形的B-Rep→CSG 问题。如图10 所示，在采用半空间分割法进行B-Rep→CSG 转换时，可先对二维图形进行转换，然后将转换结果映射至三维空间，如将图10 所示轮廓面的边映射为拉伸特征的面，再添加端面即可获得拉伸特征的CSG 表示。本文采用半空间分解法，其拉伸特征MF的B-Rep→CSG 转换步骤如下：

（1）获取拉伸特征体对应的二维图形，并对二维图形进行B-Rep→CSG 转换，获得二维图形的CSG表示，见图10（b）。

（2）将二维图形CSG 表达式中的边映射至面，如直线映射为平面、圆弧映射为圆柱面，获得两端无界的拉伸体的CSG 表示，见图10（c）。

（3）根据拉伸特征的端面情况，为步骤（2）所得的CSG 表达式添加端面，最终获得拉伸特征的完整CSG 表示，见图10（d）。

因步骤（2）可根据拉伸特征的定义直接完成映射，不再赘述。若拉伸特征的端面为单个平面，则步骤（3）可直接解决，若端面由多个面组成，则比较复杂，笔者在工程实践中采用的是递归半空间分割法。因为本文的核心是拉伸特征的识别和应用，且在工程实践中，端面多为平面，所以仅考虑端面为平面的情况，对步骤（2）和（3）不再做详细讨论。

图10 拉伸特征B-Rep→CSG 转换过程示意Fig.10 Schematic diagram of B-Rep→CSG conversion process of stretch feature

由文献［18］知，在半空间分割方法中，二维图形B-Rep→CSG 转换的难点是如何将复杂的二维图形分解为一组简单图形。如果二维图形是多边形，则将多边形分解为一组凸多边形。因为将任意多边形分解为一组凸多边形是图形学领域的经典问题，有大量优秀成果可以利用，本文仅考虑利用相关算法解决二维图形的B-Rep→CSG 转换问题。文献［19］中的多边形分解算法具有计算量小、分解所得的凸多边形边少等优点，能简化多边形的CSG 表示。如图11（a）所示的复杂多边形，用文献［19］中的基于顶点可见的多边形分解算法，得到如图11（b）所示的结果，而任意分解结果如图11（c）所示，可见文献［19］算法的分解结果更优。

图11 不同多边形分解算法效果对比Fig.11 Comparison of different polygon decomposition methods

因为cosVMPT 软件要求B-Rep 模型只能包含平面、球面、圆柱面、圆锥面和圆环面，所以当拉伸特征的拉伸面为平面或圆柱面时，所对应的二维图形的边为圆弧或直线。如图12 所示，若二维图形M2D中包含圆弧，则可通过以下方法将其转换为多边形，再采用多边形分解算法（不考虑出现自交多边形的情况）：

（1）用弦代替对应圆弧，形成多边形P2D。

（2）记录圆弧和弦包围形成的二维图形，将所有凸圆弧和凹圆弧对应的图形分别记为{conf1，conf2，…，confn} 和{concf1，concf2，…，concfm}。

那么M2D的CSG 表示为

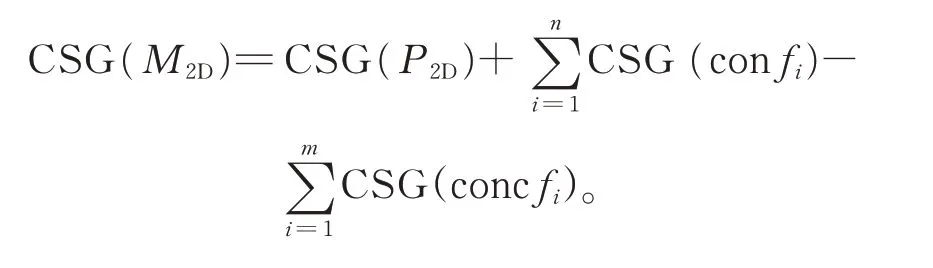
图12 轮廓面的多边形化过程Fig.12 Polygonization process of profile

3 实验与应用

本文算法已应用于我国自主核能设计软件包COSINE 的辅助建模cosVMPT 软件，其主界面如图 13 所示。 该软件基于开源造型引擎OpenCascade 7.3.0，在windows 平 台 采 用visual studio 2017 开发。 本文中的所有实验均基于cosVMPT 完成。

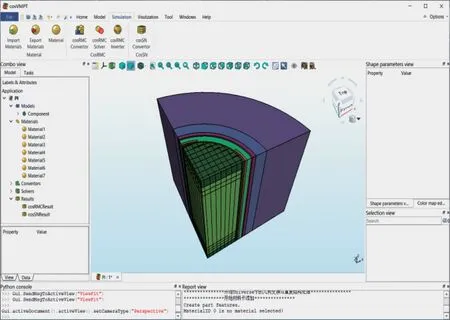
图13 cosVMPT 主界面Fig.13 The main interface of cosVMPT

首先由简单到复杂构造3 个模型，见图14 中的（1）、（2）和（3）。分别对模型进行测试，并对采用本文算法前后的转换时间和转换效果进行比较，见表1 和图14。因为半空间分割法B-Rep→CSG 转换的核心是分解复杂模型，所以图14 未采用最终的CSG表达式，而是以分解结果表示转换效果。

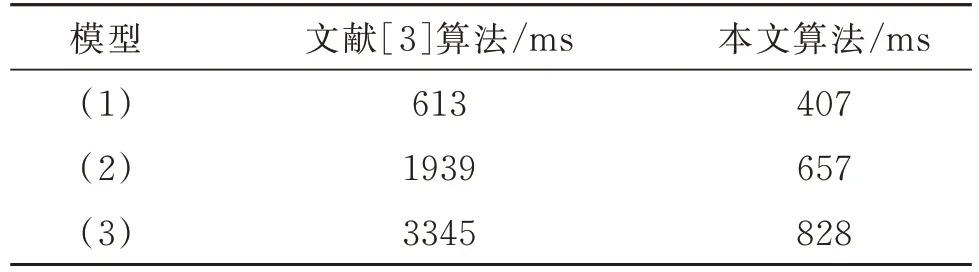
表1 转换时间比较Table 1 Time comparison of conversion

由图14 可知，本文算法的分解结果更简洁或其CSG 表示更简洁。如本文算法可将模型（2）分解为4 个子模型，而半空间分割法则将模型（2）分解为9个子模型，且本文算法分解结果更符合模型的特点，即具有更强的语义性；虽然用半空间分割法分解模型（1），子模型数更少，但其分解结果的CSG 表示更复杂，需要添加辅助分割面。由表1 可知，在转换时间上，本文算法也具明显优势，3 个模型均提速30%以上，且模型越复杂，提速效果越明显。

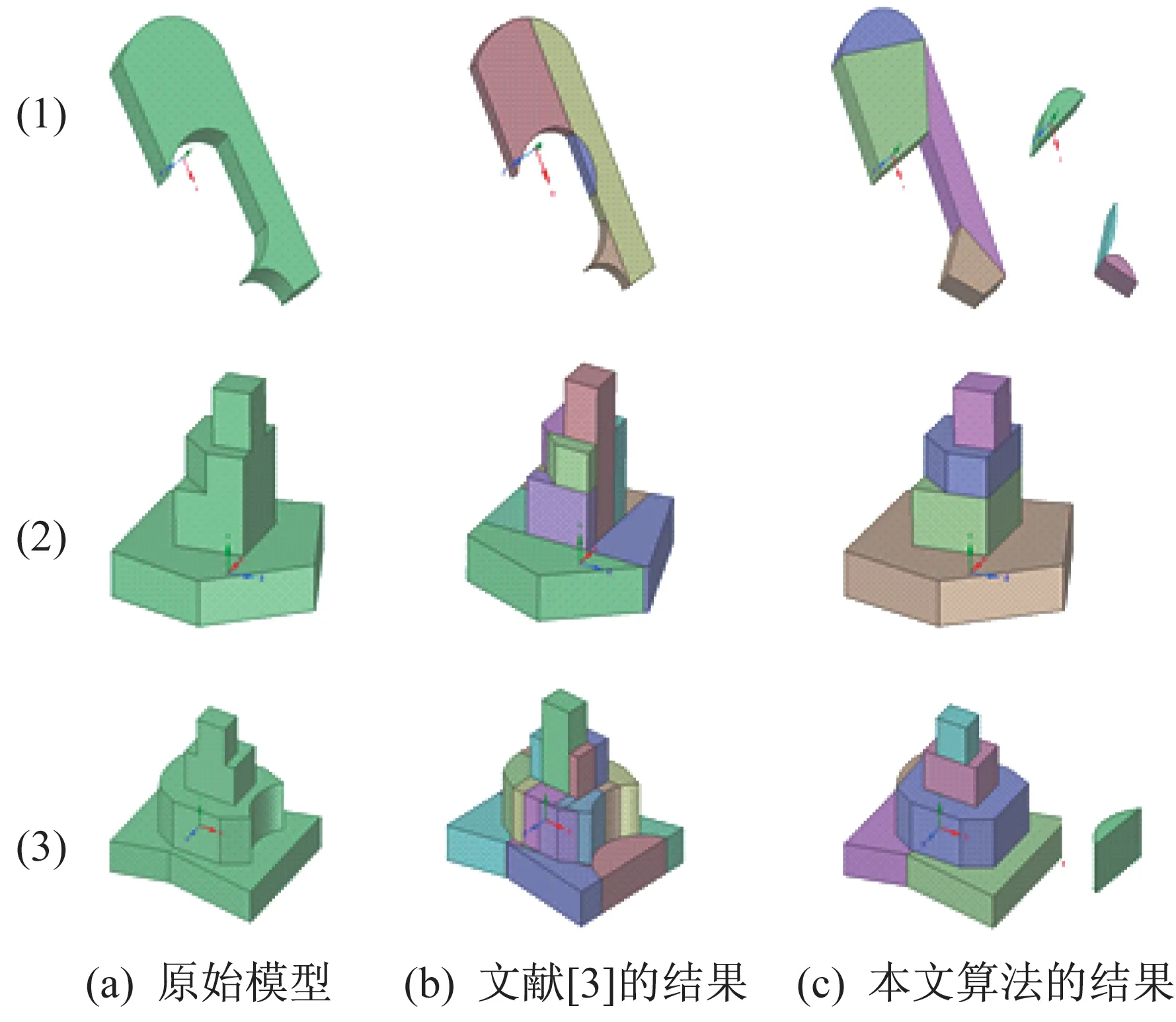
图14 测试分解结果展示Fig.14 Display of test results

用具有代表性的AP1000 裂变堆堆芯模型进行测试（如图3 所示）。AP1000 是我国引进的由美国西屋公司设计的第3 代先进反应堆，其包含665 个B-Rep 模型，所有模型均为拉伸体，采用本文算法后，B-Rep→CSG 转换时间由130 079 ms 降至7 781 ms，速度提升了39%。但由于此案例中的BRep 对象均较简单，尚难体现本文算法的优势。

本文算法的主要优势是降低了对布尔运算的依赖，提高了算法的稳定性。但因布尔运算失败具有偶然性，难以准确复现，本文尚无法用实验证明此优势。

4 结 语

半空间分割法是应用最广泛的B-Rep→CSG转换算法之一，其核心是将B-Rep 模型分解为一组简单模型，在实现过程中，依赖三维造型引擎的布尔运算，但因造型引擎的布尔运算存在失败概率，从而影响B-Rep→CSG 转换算法的稳定性，尤其对批量转换软件，不稳定性会严重影响软件的可用性和友好性。本文利用拉伸特征，将三维B-Rep 模型的B-Rep→CSG 转换问题转变为二维图形的B-Rep→CSG 转换问题，从而降低对布尔运算的依赖，提高转换算法的稳定性，同时提高了转换算法的速度。

提出了基于拉伸边的拉伸特征识别方法，通过观察和总结，得到拉伸边的相互平行性、首尾相连性、方向相反性、唯一连接性4 个特征，在此基础上提出基于平行边连接图的拉伸特征识别算法。在拉伸特征识别算法的基础上，结合基于环收缩的模型分割算法和基于顶点可见的多边形分解算法，实现了三维模型的B-Rep→CSG 转换，并在cosVMPT软件中进行了测试，测试结果验证了算法的有效性和优越性。

本文的拉伸特征识别算法依赖相互平行性、首尾相连性、方向相反性、唯一连接性等实践经验，没能对算法的完备性进行严格证明，有待今后进一步研究；另外，本文讨论的是拉伸特征，在实践中存在大量旋转特征，将旋转特征的三维问题转换为二维问题，也有待下一步研究，以进一步扩大本文算法的应用领域。