δ-BiHom-Jordan-李超代数的阿贝尔扩张和T*-扩张
2021-03-23郭双建
郭双建
(贵州财经大学数学与统计学院,贵州贵阳550025)
作为李代数的推广,Hom-李代数的引入源于物理学和李代数的双重需要,其概念由HARTWIG等在研究拟李代数时引入,并将其作为研究Witt 代数和Virasoro 代数变形的一部分[1-4]。
文献[5]引入了Hom-李超代数的概念,给出了Hom-李超代数的允许分类,验证了Hartwig-Larsson-Silvestrov 定 理 的 分 次 情 形。 随 后,文献[6]研究了Hom-李超代数的表示和上同调理论,计算了Witt 超代数的导子和第二上同调群。文献[7-9]也研究了Hom-李超代数的相关性质。
BiHom-代数是一种其定义结构上的恒等式被2 个同态α,β扭曲的代数。这类代数作为一种范畴方法被引入,是对Hom-代数的推广。文献[10]得到BiHom-代数的基础概念和结果。文献[11]使BiHom-代数得以延续和发展。随后,BiHom-李代数、BiHom-李超代数、BiHom-李着色代数和BiHom-Novikov 代数在文献[12-14]中有更多的应用。
作为Jordan-李超代数的推广[15],文献[16]引入δ-Hom-Jordan-李超代数的定义,并详细研究其表示和T*-扩张。文献[17]引入δ-BiHom-Jordan-李超代数的定义,并研究其表示。本文继续研究δ-BiHom-Jordan-李超代数的性质,引入δ-BiHom-Jordan-李超代数的阿贝尔扩张,证明与任意阿贝尔扩张相关联的表示和2-余循环。利用上同调理论和表示δ-BiHom-Jordan-李超代数的T*-扩张,证明特征不为2 的代数闭域上的有限维幂零二次δ-BiHom-Jordan-李超代数与幂零δ-BiHom-Jordan-李超代数的T*-扩张等距。另外,从上同调角度给出了T*-扩张的等价性。
1 预备知识
定义1[17]δ-BiHom-Jordan-李超代数为由向量超空间L、双线性映射[⋅,⋅]:L⊗L→L和2 个线性映射α,β:L→L组成的四元组(L,[⋅,⋅],α,β),对任意的x,y,z∈L,有
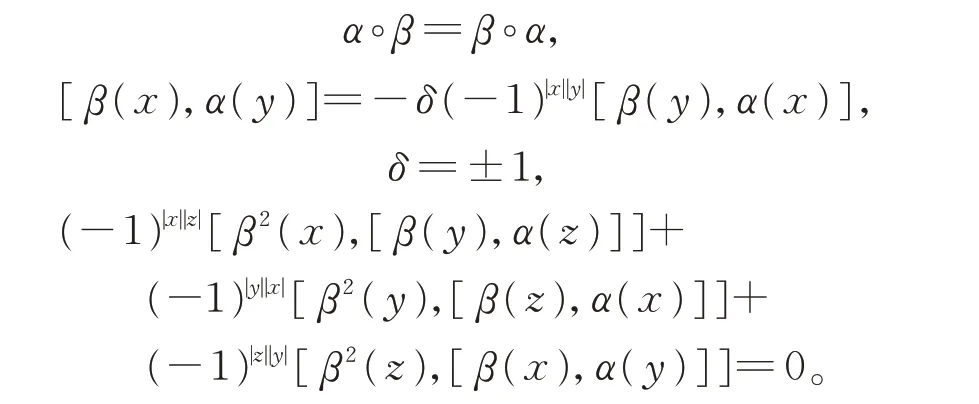
当δ=1 时 为BiHom-李超代数;当δ=−1 时 为BiHom-Jordan-李超代数。
定 义2[17](i)若α和β为代数态射,则称δ-BiHom-Jordan-李代数(L,[⋅,⋅],α,β)是保积的,即对 任 意 的x,y∈L,有α([x,y])=[α(x),α(y)],β([x,y])=[β(x),β(y)]。
(ii)若α和β为代数自同构,则称δ-BiHom-Jordan-李代数(L,[⋅,⋅],α,β)是正则的。
定 义 3[17]设(L,[⋅,⋅ ],α,β) 为 保 积δ-BiHom-Jordan-李超代数。L上的表示为四元组(M,ρ,αM,βM),其中M是线性空间,αM,βM:M→M是2 个交换线性映射,ρ:L→End(M)是线性映射,使得对所有u,v∈L,有设(L,[⋅,⋅],α,β)为正则δ-BiHom-Jordan-李超代数,Ck(L;M)表示L上具有M值的K-上链集,且是从L×…×L(k个)到M的线性映射:
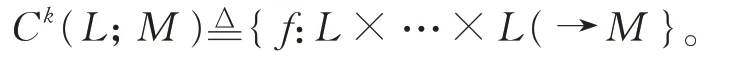
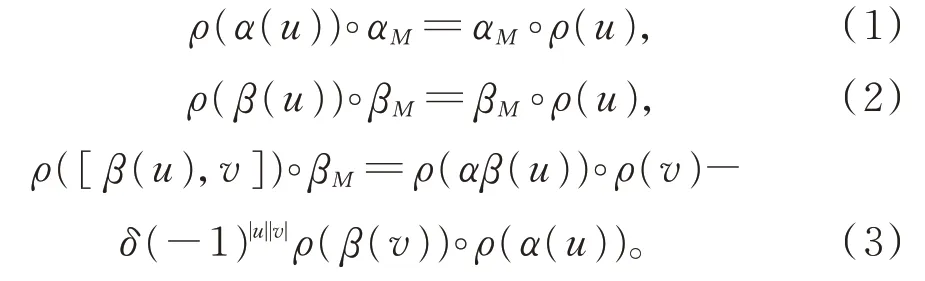
定义L上具有M值的BiHom-上链为K-上链f∈Ck(L;M),使得其与α,β和αM,βM相容,即

所以
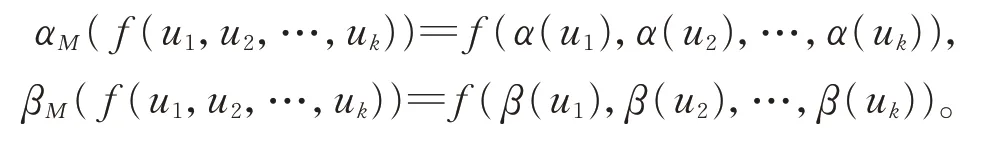

定义线性映射

2 δ-BiHom-Jordan 李超代数的阿贝尔扩张
定 义4设(L,[⋅,⋅],α,β),(V,[⋅,⋅]V,αV,βV)和为δ-BiHom-Jordan 李超代数,为δ-BiHom-Jordan 李超代数的态射 。 如果 Im(i)=Ker(p),Ker(i)=0,且Im(p)=L,则有δ-BiHom-Jordan 李超代数的正合序列:
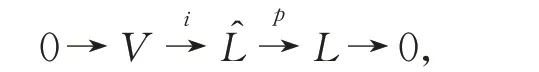
称为L对V的扩张,用表示。如果V是ˆ的阿贝尔理想,即对所有的u,v∈V,有,则称V为阿贝尔扩张。ˆ→L的截面σ由线性映射σ:L→ˆ组 成,使得p∘σ=idL,σ∘α=,σ∘β=。
定义5如果存在δ-BiHom-Jordan 李超代数的态射F:˜,使得

可换,则δ-BiHom-Jordan 李超代数的2 个扩张是等价的。设为L对V的阿贝尔扩张,为截面,则θ:L→End(V)的映射
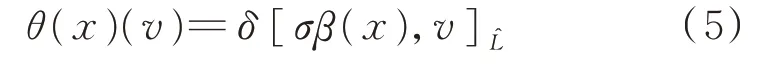
对所有x∈L,v∈V均成立。
定理1设(V,αV)和(L,α)为保积δ-BiHom-Jordan 李超代数,则(V,αV,βV,θ)是(L,α,β)的表示,且不依赖于截面σ的选取。同时,等价阿贝尔扩张有相同的表示。
证明首先,如果选择另一个截面,则存 在u∈V,使得p(σβ(x)−σ′β(x))=β(x)−β(x)=0⇒σβ(x)−σ′β(x)∈V⇒σ′β(x)=σβ(x)+u。 注意到对所有的u,v∈V均成立,所以

表明θ与截面σ的选取无关。
其次,证明(V,αV,βV,θ)是(L,α,β)的 表 示。对任意的x,y∈L,v∈V,有

因此,可得式(1)和式(2)。
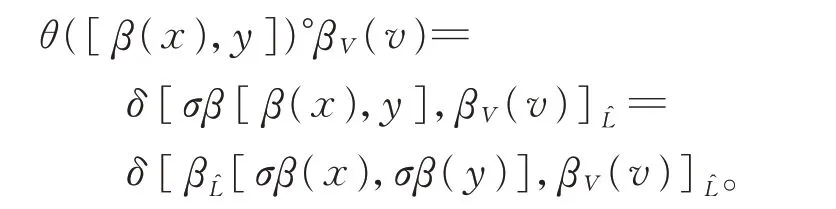
最后,

因此,可得式(3)。
接下来,验证等价阿贝尔扩张有相同的θ。
假 设ELˆ和EL˜是等价的阿贝尔扩张,且是 满 足F∘i=j,q∘F=p的δ-BiHom-Jordan 李超代数态射。分别选取p和q的线性截面σ和σ′,则有qFσ(x)=pσ(x)=x=qσ′(x),因此,

且
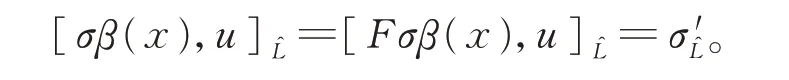

对所有的x1,x2,x3∈L成立。
定 理2设为L对V的阿贝尔扩张,则式(6)中的ω是以V为系数的L上的2-余循环,式(5)中的θ为L上的表示。
证明在式(4)中,令f=ω,ρ=θ,对任意的x,y,z∈L,有

因此,ω是2-余循环。
3 δ-BiHom-Jordan 李超代数的T*-扩张
定理3设(L,[⋅,⋅],α,β)为δ-BiHom-Jordan李超代数,若

为αβ-不变量,对任意的x,y,z∈L,
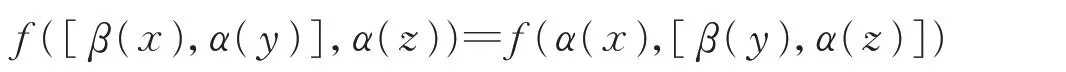
对称,且

则称L上的双线性形式f是非退化的。
若I⊆I⊥,则称L的子空间I是迷向的。
定 义 6设 (L,[⋅,⋅],α,β) 为δ-BiHom-Jordan-李超代数,如果L具有非退化不变对称双线性 形 式f,则 称(L,f,α,β)为 二 次δ-BiHom-Jordan李超代数。
设(L′,[⋅,⋅]′,α′,β′)是 另 一 个δ-BiHom-Jordan李超代数,如果存在δ-BiHom-Jordan 李超代数同构φ:L→L′,使得

则称2 个二次δ-BiHom-Jordan 李超代数等距。
引理1设ad 是δ-BiHom-Jordan 李超代数(L,[⋅,⋅],α,β)的伴随表示,考虑L的对偶空间L∗,定义2 个同态为

则映射π:L→End(L∗),

为L在上的表示当且仅当
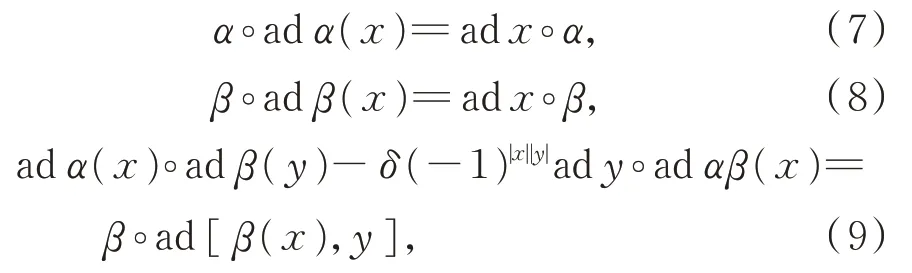
并称π为L的余伴随表示。
证明首先,由于

类似地,有

于是,

则
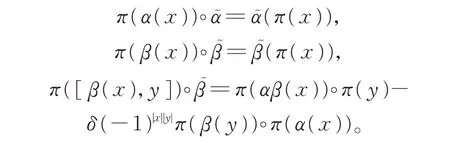
因此,π是L在上的表示。
引 理 2设 (L,[⋅,⋅],α,β) 为δ-BiHom-Jordan-李超代数,ω:L×L→L∗为双线性映射。假设存在余伴随表示

则(L⊕L∗,[⋅,⋅],α′,β′)为δ-BiHom-Jordan-李超代数当且仅当ω:L×L→L∗是2-余循环。
证明对任意的x+f,y+g,z+h∈L⊕L∗,有

类似地,有
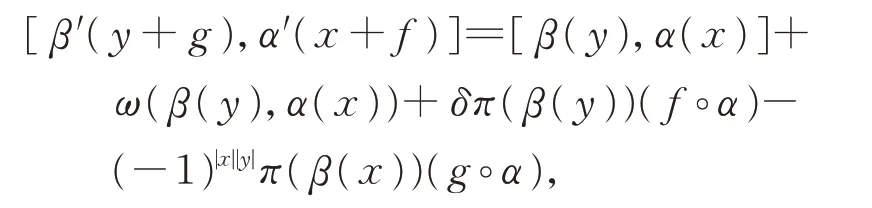
于是
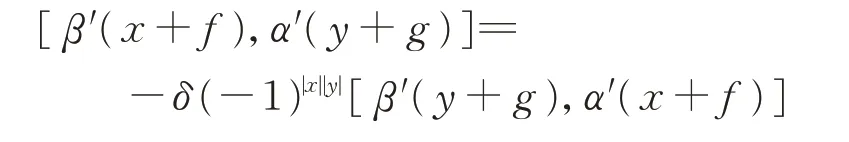
当且仅当

容易验证 Jacobi 等式成立当且仅当δd−1,1ω(x,y,z)=0。
显然,L∗为(L⊕L∗,[⋅,⋅],α′,β′)的交换BiHom-理想,L与L⊕L∗/L∗同构。设qL在L⊕L∗上具有对称双线性形式,对所有x+f,y+g∈L⊕L∗,有
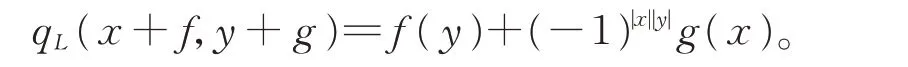
引理3设L,L∗,ω,qL同前,则(L⊕L∗,qL,α′,β′)为二次δ-BiHom-Jordan-李超代数当且仅当ω是Jordan 循环的,即存在x,y,z∈L,使得
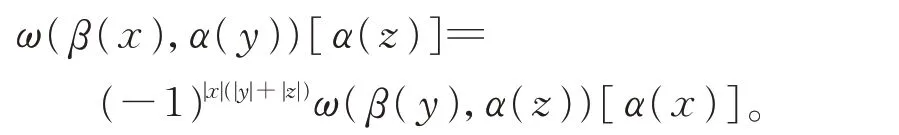
证明如果x+f与L⊕L∗中的元素y+g正交,那么有f(y)=0 和g(x)=0,即x=0 和y=0。因此,对称双线性形式qL是非退化的。
对任意的x+f,y+g,z+h∈L⊕L∗,一方面,

另一方面,

证毕。
对于Jordan 循环的2- 余循环ω,称二次δ-BiHom-Jordan 李超代数(L⊕L∗,qL,α′,β′)为L的T∗-扩张,并用表示。
引理4设(L,[⋅,⋅],α,β)为δ-BiHom-Jordan李超代数 。 定义 导出级数(L(n))n≥0:L(0)=L,L(n+1)=[L(n),L(n)],中 心 递 减 级 数(L(n))n≥0:L(0)=L,L(n+1)=[L(n),L],称L是可解性和幂零性的(长度为k)当且仅当存在(最小)整数k,分别使得L(k)=0 和Lk=0。
定理4设(L,[⋅,⋅],α,β)为δ-BiHom-Jordan李超代数。
(i)如果L可解的长度为k,则T∗-扩张可解(幂零)的长度为r,其中k≤r≤k+1(k≤r≤2k−1)。
(ii)如果L可被分解为L的2 个δ-BiHom-理想的直和,则平凡的T∗-扩张T∗0L也如此。
证明(i)首先,假设L可解的长度为k。由于意 味着由于L∗是阿贝尔的,可得T∗ω L可解的长度为k或k+1。
假设L幂零的长度为k。 由于设
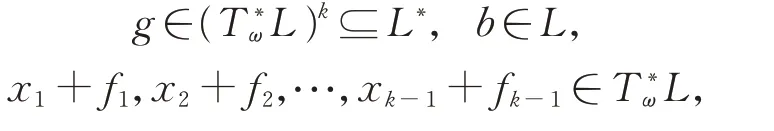
有

(ii)假设0 ≠L=I⊕J,其中I和J为L的2 个δ-BiHom-理想。令I∗(或J∗)表示在J(或I)上等于零的L∗中所有线性形式的子空间。由
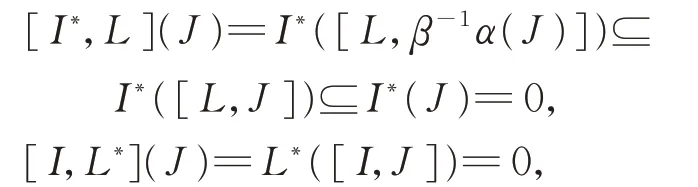
那么

则是L的BiHom-理想,也如此。
证毕。
为证明δ-BiHom-Jordan 李超代数的T∗-扩张准则,需要以下引理。
引理5设(L,qL,α,β)为维数为n(偶数)的二次δ-BiHom-Jordan 李超代数,I是L迷向的n/2 维子空间。 如果I是L的 BiHom- 理想,则[β(I),α(I)]=0。
证 明由 于dimI+ dimI⊥=n/2+ dimI⊥=n,I⊆I⊥。如果I是L的BiHom-理想,那么

则[β(I),α(I)]=[β(I),α(I⊥)]⊆α(L)⊥=0。
引理6设(L,qL,α,β)为特征不等于2、维数为n的二次δ-BiHom-Jordan 李超代数,则(L,qL,α,β)与(,qB,α′,β′)是等距的当且仅当n是偶数且(L,qL,α,β)包含维数为n/2 的迷向的BiHom-理想I。特别地,
证明充分性。由于dimB= dimB∗,dim是偶数,则dimqB(B∗,B∗)=0,即B∗⊆(B∗)⊥和B∗是迷向的。
必要性。假设I为L上一个n/2 维迷向的BiHom-理想。由引理5,有[β(I),α(I)]=0。设和p:L→B是典范投影 。 由 于char(K)≠2,在L中取一个迷向的补子空间B0,即L=B0+I和B0⊆B0⊥,则有B0=B0⊥。
设满足
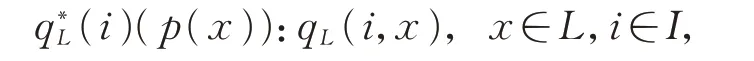
容易验证是线性同构的。此外,具有以下性质:

定义齐次线性映射:ω:B×B→B∗,

设φ:L→B⊕B∗,

容易验证φ是代数同构的。
下证φ是等距的。事实上,
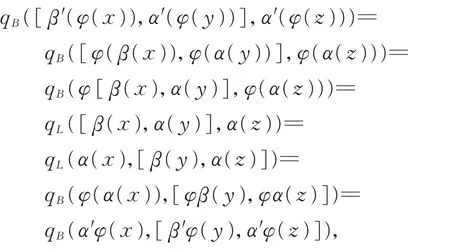
表明qB是一个非退化不变对称的双线性形式,因此(B⊕B∗,qB,α′,β′)是 二 次δ-BiHom-Jordan 李 超 代数,从而可得B的T∗-扩张,于是有(L,qL,α,β)与是等距的。
设(L,[⋅,⋅],α,β)为δ-BiHom-Jordan 李超代数,ω1:L×L→L∗和ω2:L×L→L∗是2 个不同的Jordan 2-余循环。如果δ-BiHom-Jordan-李超代数的同构是BiHom-理想L∗上的恒等式,并由此导出因子δ-BiHom-Jordan 李超代数上的恒等式,则称T∗-扩张是等价的。如果T∗-扩张和等价,且φ等距,则称它们是等距等价的。
引理7设(L,[⋅,⋅],α,β)为特征不等于2 的δ-BiHom-Jordan 李超代数,ω1和ω2是2 个 不同 的Jordan 2-余循环,则有
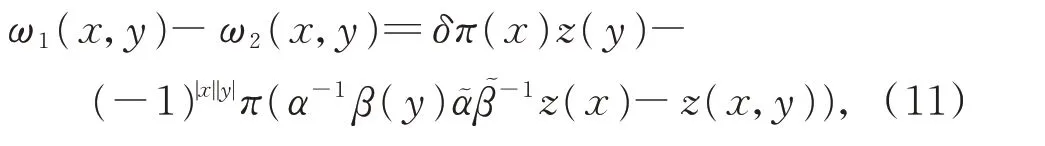
则z的对称部分定义为
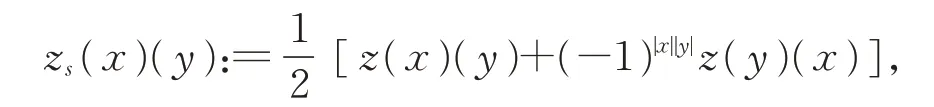
zs可诱导出L上的对称不变双线性形式。
(ii)与等距等价当且仅当z∈C1(L,L∗)使得式(11)成立,且z的对称部分zs等于零。
证 明(i)与等价当且仅当δ-BiHom-Jordan 李超代数的同构
满足Φ|L∗=1L∗和x−Φ(x)∈L∗,x∈L。

另一方面,

由于Φ同构,则式(11)成立。
必要性。如果存在z∈C1(L,L∗),满足式(11),定义

满足Φ(x+f):=x+z(x)+f。
易证Φ是δ-BiHom-Jordan 李超代数的同构,存在x∈L,使得Φ|L∗=1L∗,x−Φ(x)∈L∗,则与等价。
考虑由zs诱导的对称双线性形式
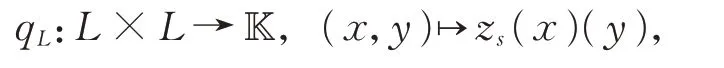
且


由于ω1和ω2都是Jordan 2-余循环,所以此两个方程的右边相同。因此
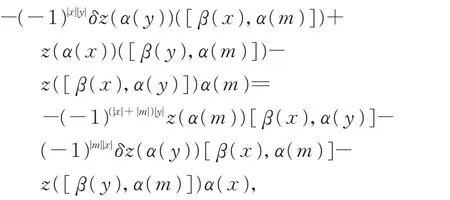
即

由于char(K)≠2,因此
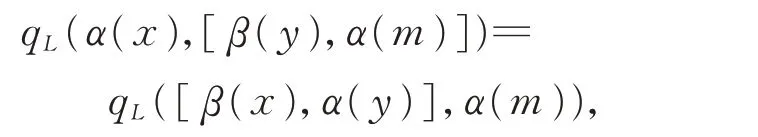
即证明了zs诱导的对称双线性形式qL是不变性的。
(ii)同构Φ的定义同(i),对任意的x+f,y+g∈L⊕L∗,有
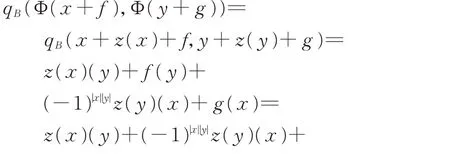

因此,Φ是等距的当且仅当zs=0。
