光滑函数实根计算的渐进显式公式
2021-03-23祝平陈小雕马维银姜霓裳
祝平,陈小雕,*,马维银,姜霓裳
(1.杭州电子科技大学计算机学院,浙江杭州 310018; 2.香港城市大学 机械工程学系,中国香港; 3.杭州电子科技大学理学院,浙江杭州 310018)
0 引 言
求根在计算机辅助几何设计[1]、计算机图形学[2-3]、机器人技术[4]及地磁导航中具有广泛应用。理论上,利用结式等消元方法,可将多项式方程组转化为一元多项式方程。本文只讨论单变量方程的求根问题,线性方程组的其他求解方法可参见文献[1,5-6]等。
计算稳定性与计算效率是求根的2 个关键问题。效率因子(efficiency index,EI)常用于衡量算法的计算效率。设某算法的收敛阶为p,需进行n次函数计算(functional evaluation,FE),则对应的EI 定义为p1/n。文献[7]猜想:任何需要n次FE 的求根方法对应的收敛阶都不会超过最优次数2n-1。
下文着重介绍求解光滑函数实根的3 种方法。
(1) 类牛顿法,包走 Newton,Halley 和Ostrowski 法[8-10]。从初始值开始,获得近似于根的点序列,通常用第k个点的信息计算第(k+1)个点,计算性能取决于初始值的选取,当初始值选取错误时,易发散。文献[9-10]以收敛阶8 得到了最佳效率指数,但不易扩展至更高收敛阶[11]。理论上相应的区间方法可提高计算稳定性,但将耗费更多的计算时间[12-13]。基于笛卡尔法则与Sturm 定理的多项式求根方法虽具有较好的计算稳定性,但收敛速度较低。
(2)基于Bernstein-Bézier 形式的裁剪法[1,14-17]。利用Bernstein-Bézier 形式具有的系数扰动稳定性特点,通过不断裁剪不包含实根的小区间,获取较好的计算稳定性[18],收敛速度通常优于Sturm方法[19]。
(3)渐进法[20-21]。从包含根的初始区间开始,利用前k个点(而非仅第k个点)的信息渐进式计算第(k+1)个点。其基本思想是利用分子的线性多项式逼近给定的光滑函数,从而逼近多项式对应的实根,得到较精确的解。对于区间内只包含一个根的情况,逼近多项式的实根被限制在给定区间,且近似效果渐进式递增,即使没有好的初始值也可确保收敛。
本文提出了一种基于重新参数化方法(reparamaterization-based method,RBM)的非线性方程求根方法,直接寻求重新参数化函数并给出实根的渐进式近似公式,得到了较现有渐进法更高的计算效率,并兼具渐进法的计算稳定性。
1 RBM
非多项式函数的实根隔离是一项艰巨的工作,超出了本文的讨论范围,当f(t)为多项式时,可通过实根隔离方法使每个区间只含有一个实根[1,13,22-23]。本文假设函数f(t)在给定区间[a,b]内具有唯一单根t*。
1.1 思路及算法原理
首先 ,设函数Ri(t) 插值f(t) 于t=t0,t1,…,ti∈[a,b],即
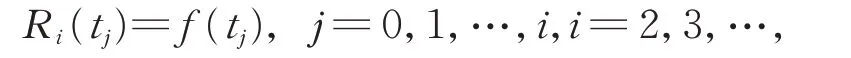
其中,t0=a和t1=b。
则Ri(t)和f(t)对应的无穷级数在区间[a,b]内收敛,即
通过渐进式插值更多的点可得到更小的逼近误差。
设φi(s)为重新参数化函数,使得φi(sj)=tj且
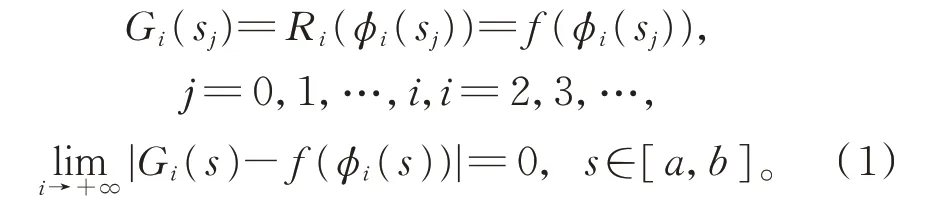
若s*∈[a,b]满足Gi(s*)=0,则类似于式(1),可得

由式(2),φi(s*)可作为t*的近似值。
然后,做以下技术处理,以方便高效地获取相应的s*和重新参数化函数φi(s):
(ⅰ)用有理多项式L(s)/gi(s)作为Gi(s)的形式,其中L(s)为满足L(a)=f(a)和L(b)=f(b)的一次多项式,则s*对应为L(s)的根,可较方便地求解相应值。
(ⅱ)用重新参数化函数φi(s)作为次数为i的多项 式,并 用(s/gi(s),L(s)/gi(s))插 值(t,f(t))。于是,每 给 定 一 个tj,由(sj/gi(sj),L(sj)/gi(sj))=(tj,f(tj)),可得

式(3)是关于sj的一次多项式,可方便地求解sj对应的值。给定t0,t1,…,ti,由式(3),可得到对应的s0,s1,…,si。进而由i+1 个线性方程:

确定相应的多项式φi(s)。
最后,由式(2),得φi(s*)的近似实根t*。
本文方法无需计算gi(s)的表达式,计算效率比现有的渐进法更高,且兼具渐进法良好的计算稳定性。
1.2 算法概述
引入文献[24]中的定理3.5.1,即
定理1令w0,w1,…,wr为区间[a,b]内的r+1个不同点,并且n0,w1,…,wr为r+1 个大于0 的整数,令N=n0+n1+…+nr,假设g(t)是次数为N的多项式,使得g(i)(wj)=f(i)(wj),i=0,1,…,nj−1,j=0,1,…,r。存在ξ0(t)∈[a,b],使得
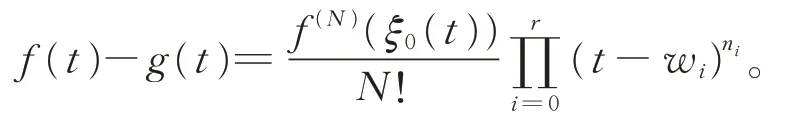
设t0=a,t1=b,可验证

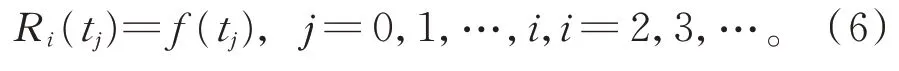
求解式(6),得到ti+1。
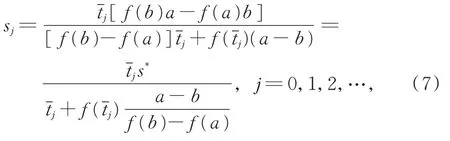
其中,s0=t0,s1=t1,sj为线性方程
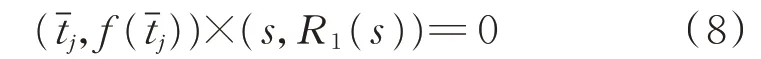
的实根。令φi(s)为i次多项式,i=1,2…,使得


由式(7)和式(9),得到渐近式
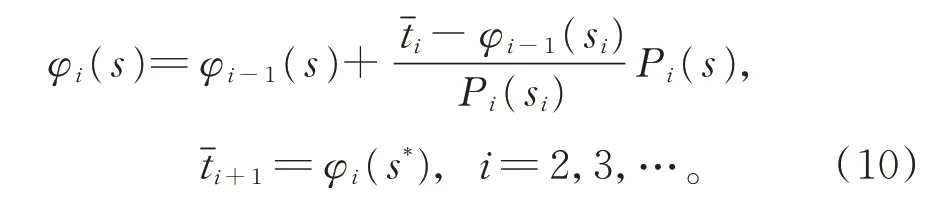
式(10)的求根步骤为
算法1求解区间[a,b]内f(t)的实根t*。
输入函数f(t)、区间[a,b]和误差精度ε。
输出实根t*的近似值。
步骤 1令t2,i=2。
步骤2若转步骤4。否则,转步骤3。
步骤3由式(10),计算φi(s)和并令i=i+1,转步骤2。
步骤4输出即t*的近似值。
1.3 收敛阶
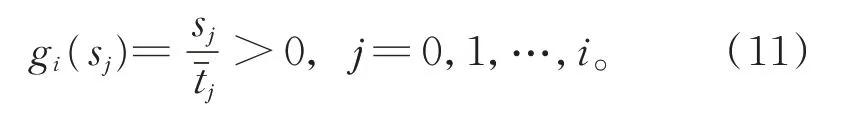
由式(8)和式(11),可得
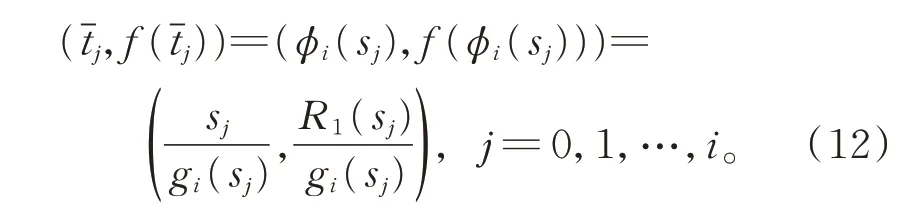
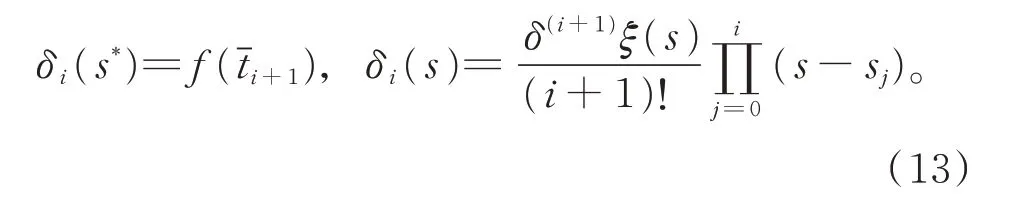
定理2设则有

其中,h=b−a,为区间[a,b]的长度。
证明由式(13),有

由式(15),当i=2 时,有

由式(7),可得
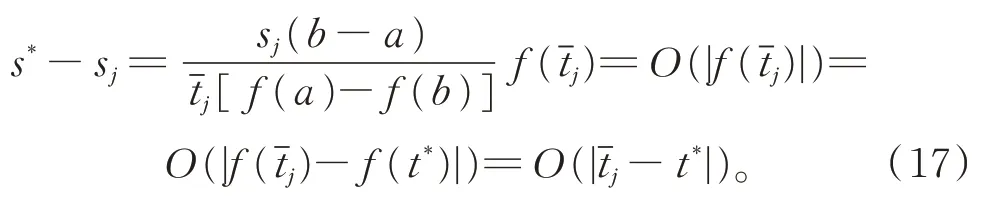
由式(15)和式(17),可得
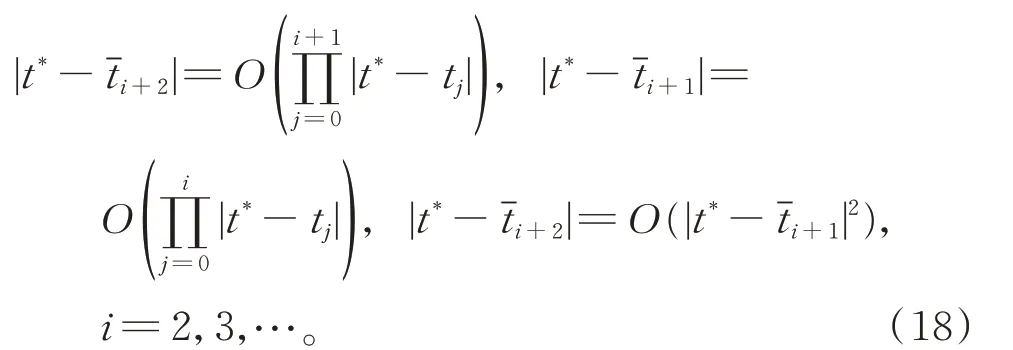
由式(16)和式(18),可得式(14)。
证毕。
定 理3设κ1,κ2∈[a,b],若2|κ2−t*|<|κ1−t*|,则2κ2−κ1和κ1将包住t*。
证明不失一般性,不妨设κ1<κ2,则有

即

由κ1<κ2和式(19),可得
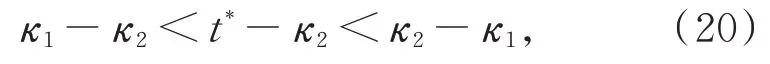
式(20)等价于

即2κ2−κ1和κ1包住了t*。
证毕。
注1在式(10)中,所有ti和si(i=2,3,…)应落在给定区间[a,b]内,但在某些情况下,ti或si可能落在区间[a,b]外。由定理3 知,通过获得更小的子区间,并用算法1 得到相应的实根t*。
1.4 RBM 示例
先用简单且方便验证的例子说明本文算法。
例 1令f1(t)=(t−0.25)(2 −t)(t+5)2,t∈[0,1],在区间[0,1]内有一个单根t*=0.25。令可得线性函数L(s)=−12.5+39.5s及s*=由式(3),可得由式(6)和式(3),可分别得到t3=φ2(s*)≈0.040 274,s3≈0.041 84。
更多ei=|ti−t*|的值(i=3,4,…,9),见表1。本例中,精度设置为小数点后100。

表1 例1 中不同i 值下逼近误差ei=|ti−t*|的对应结果Table 1 The corresponding results of the approximation error ei=|ti−t*|in example 1 when different i
2 不同方法的定性比较
表2 给出了3 类方法的符号,本节将对此3 类方法进行定性比较。所有示例均在具有12 GB 内存和4 核2.2 G CPU 的PC 上 用Mathematica 软 件 进 行 测试,时间单位为ms。
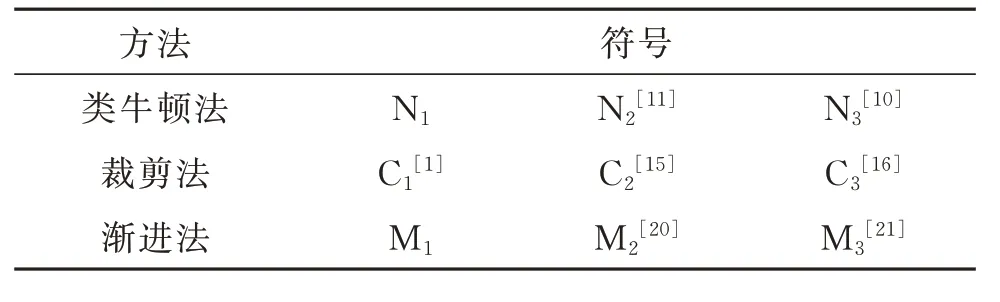
表2 3 类方法的符号Table 2 Symbols of three types of methods
首先,比较不同方法的渐进效率因子(AEI)。AEI 与EI 类似,通常用于测量算法的计算效率,其含义为每增加一次FE 所对应的收敛阶,AEI 越大效率越高。表3 为不同方法的计算效率比较,其中nfe、CR、AEI 分别表示FE 次数、收敛阶和渐近效率因子。表3 中,从第2 步或第3 步开始,渐进法M1,M2和M3每增加一次FE 可获取的收敛阶为2。结果表明,渐进法较类牛顿法和裁剪法具有更高的计算效率。
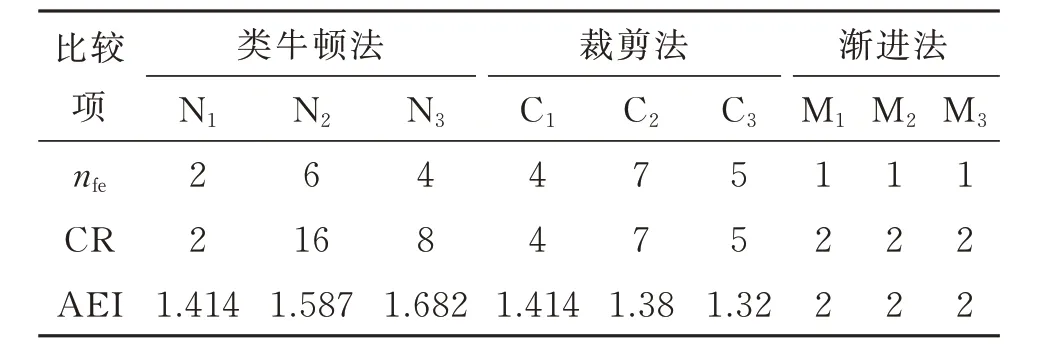
表3 3 类方法的计算效率比较Table 3 Comparisons of computational efficiency of three types of methods
其次,表4 中,nfe为不同方法达到收敛阶为16 时所对应的FE 次数。理论上,C1,C2和C3分别需花费4n,7n和5n次FE 才能获得收敛阶4n,7n,5n,且每步裁剪将分别增加4,7 和5 次FE;而本文方法M1花费n次FE 可 达 到 的 收 敛 阶 为3 ⋅2n−2(n=3,4,…),每增加一次FE 可达到的收敛阶为2。因此,M1较Ci(i=1,2,3)更灵活和高效。
最后,表5 为AEI 为2 时不同渐进法Mi(i=1,2,3)在第n步的计算成本比较,其中nfe,na,nm分别表示FE 的次数、加(减)法运算的次数和乘(除)法运算的次数。由表5 可知,M1比M2和M3的计算效率更高,且当n较大时越为有利。

表4 收敛阶为16 时对应的FE 次数的比较Table 4 Comparison results on FE times under convergence rate 16

表5 AEI 为2 时Mi在第n 步的计算成本比较Table 5 Comparison of computational cost of the n-th step in Mi under AEI 2
3 实例及讨论
用3 个实例,对不同方法进行了比较。总体来说,M1具有与裁剪法相当的计算稳定性和更高的计算效率、比类牛顿法更高的计算稳定性和更高的计算效率、与渐进法相当的收敛阶和更高的计算效率。
3.1 M1与裁剪法的比较
对M1与裁剪法C2[15]和C3[16]进行了比较。理论上,C2和C3可以计算多项式在给定区间内的所有实根。计算多项式在某个区间内的唯一单根,M1的效果更好,可将其作为裁剪法的补充。C2[15]和C3[16]在每个裁剪步骤中分别需要7 和5 次FE,并且第i个裁剪步骤子区间的长度为ei(i=1,2,…)。表6 中,M1每步需花费5 次FE,第i个误差ei映射至|t5i−1−t*|,使得M1中有5i次FE。平均计算时间与精度有关,在本文中,若无特别说明,精度为小数点后20 位。为更准确地测试对应的收敛阶,将最大精度设置为小数点后3 000 位。
例2测试以下4 个多项式函数:

区间[0,1]内分别有1 个单根1/4,1/5,1/3 和2/3。表6 为4 个多项式函数的近似误差和计算时间,其中,计算时间和CR 分别表示每个迭代步骤的平均计算时间(精度为小数点后100 位以下,单位为ms)和平均收敛阶。M1、C2和C3的收敛阶CR 分别为32,7,5。M1每步的计算效率是C2、C3的10~50 倍。对于f2(t),M1的e3可达5.1×10−2011,对应的有效精度位数为[20,3 000]。结果表明,M1的性能较C2和C3更佳。
给定误差为10−16,测试了例2,结果见表7。其中,nc表示所需的(裁剪)步数,Tc表示总的计算时间(ms)。表明M1,C2和C3可在2 个(裁剪)步骤内达到给定的误差(10-16)要求,并且M1的计算效率更高,约为C2和C3的7~30 倍。由于M1为渐进法,在获取tk时,可随时在任意k处停止,所需步骤较少,因此计算效率较高。
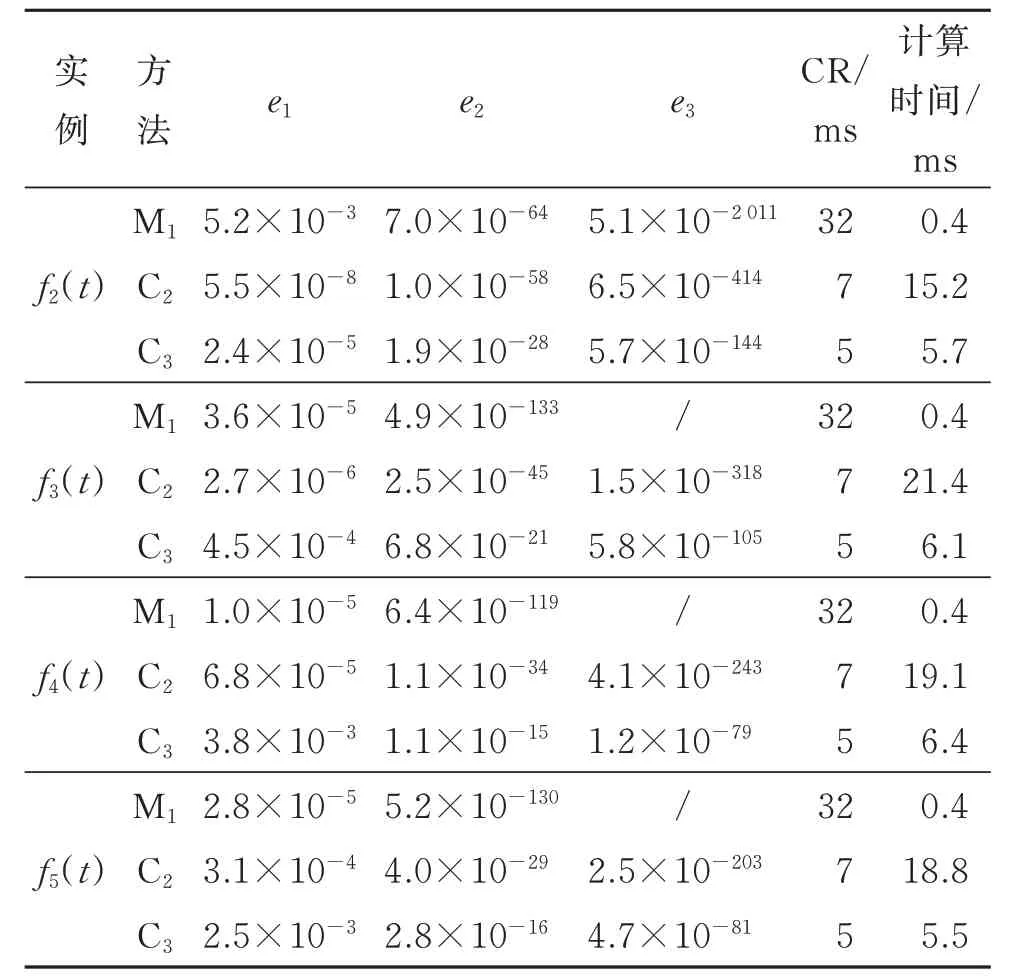
表6 例2 中4 个多项式函数在不同方法下的误差和计算时间比较Table 6 Comparisons of the error and computational time of 4 polynomial functions in different methods of example 2
3.2 渐进法与类牛顿法的比较
将渐进法(M1,M2[20]和M3[21])与类牛顿法(N2[11]和N3[10])进 行 了 比 较。N2和N3的每个迭代步分别需花费6 和4 次FE,渐进法每个迭代步需花费6 次FE,总共需化费12 次FE。
例3测试3 个非多项式函数,比较渐进法M1,M2,M3和类牛顿法N2,N3。3 个 非多项式函数分别为f6(t)=(t−1/2)[esin(10(t−π))+4(t−π)−1],t∈[3,3.3],f7(t)=tanh(2t−π/25),t∈[−0.5,0.5],f8(t)=−1/t+sin(t)+1,t∈[0.01,1.3]。其单根分别为由定理3知,可用一个初始值得到一个包含实根的小区间。表8 所列为每步的逼近误差和收敛阶。由表8 可知,对于f6(t)和f7(t),N2和N3收敛至正确结果;而对于f8(t),N2在ta=5.334 7 附近发散,N3则收敛至错误解tb=16.933。3 种情况下,渐进法均能收敛至正确结果。因此,渐进法M1,M2和M3的收敛阶相差不大,且均较类牛顿法N2和N3的收敛速度快得多。表9为在不同有效位数下运行12 次FE 的总计算时间。由表9 可知,M1,N2和N3的计算效率相当,均较M2和M3好。M1在相同时间内获得最小的逼近误差,并在给定的相同误差下,计算效率最高。

表7 4 个多项式函数在不同方法下的裁剪步数nc和计算时间Tc比较(误差精度为10−16)Table 7 Comparisons of clipping steps nc and computational time Tc of 4 polynomial functions under different methods(error tolerance is 10−16)
上述结果表明,在方法M1,M2,M3,N2和N3中,M1性能最好。

表8 3 个非多项式函数在不同方法下的逼近误差比较Table 8 Comparisons of approximation errors of 3 non-polynomial functions in different methods
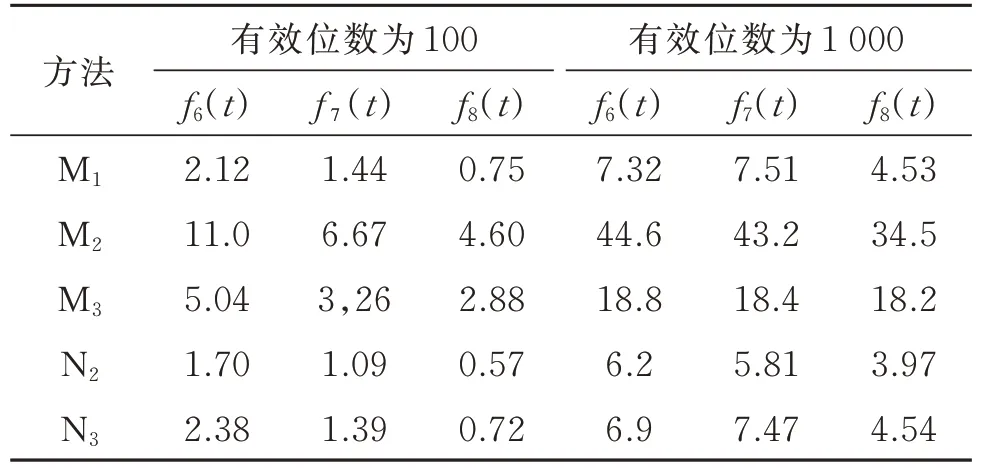
表9 3 个非多项式函数在不同方法下运行12 次FE 的时间比较Table 9 Comparisons of the computational time of three functions with cost of twelve functional evaluations under different methods 单位:ms
3.3 多根情况讨论
(1)考虑如何获取包含一个根的区间。设在初始值x0下,x1通过牛顿法或其他迭代方法得到。若2|x1−t*|<|x0−t*|,t*是f(t)的根,由定理3,t*被x0和2x1−x0所包围。因此,通过选取适当的初始值x0可得到一个包含实根的小区间。
(2)考虑区间内包含重根的情况,k为实根的重数,k≥2。若k为偶数,利用Ai(s)=(s/gi(s),L(s)/gi(s))逼近C1(t)=(f(t),f′(t));否则,利用Ai(s)逼近C2(t)=(f′(t),f(t))。理论上,估算k值且利用Ai(s)逼 近(f(k−2)(t),f(k−1)(t))是最好的选择,有利于提高收敛阶。
(3)考虑区间内可能包含2 个或多个根的情况。若给定多项式函数,则一种可行的方法是将其转换为Bernstein-Bézier 形式,并利用其控制多边形的零点将给定的区间分为若干个子区间;对每个子区间,用与(1)相同的方法进行实根隔离。对于非多项式情况,可将区间采样为多个较小的子区间,并用与(1)相同的方法将其迭代拆分为若干个包含一个根的子区间。
例4用RBM 计算Wilkinson 多项式

在区间[0,25]内的实根。该Wilkinson 多项式有20个实根Wi,i=1,2,…,20(参见文献[15]中的例6)。首先,计算相应控制多边形的零点,即{0.27,1.55,2.83,4.11,5.38,6.65,7.92,9.19,10.46,11.73,13.007,14.27,15.54,16.81,18.07,19.34,20.61,21.87,23.14,24.40},并将区间[0,25]划分为20 个子区间,其中有16 个子区间包含W(t)的1 个或2 个根。本文选取其中的3 个子区间Λ1=[0.27,1.55]、Λ2=[2.83,4.11]、Λ3=[16.81,18.07]用以说明更多细节。此3 个子区间分别包含1 个、2 个、2 个根。可将RBM 直接应用于Λ1,因为W(t)在其2 个端点的函数值异号;对于Λ2和Λ3,可选择区间中点作为分界点,将每个区间拆分为2 个子区间,每个子区间都包含1 个根。然后,将RBM 应用于子区间,由注1的方法获得优化区间。本例中,区间[0.27,1.55]、[2.83,4.11]、[16.81,18.07]对应的优化区间为Γ1=[0.99,1.0034]、Γ2=[2.83,3.004]、Γ3=[17.988,18.07]。如表10 所示,在误差ei映射到重新参数化函数φi(t)的情况下,RBM 的效果较好,表明用RBM 处理多根情形也具有较好的计算稳定性。
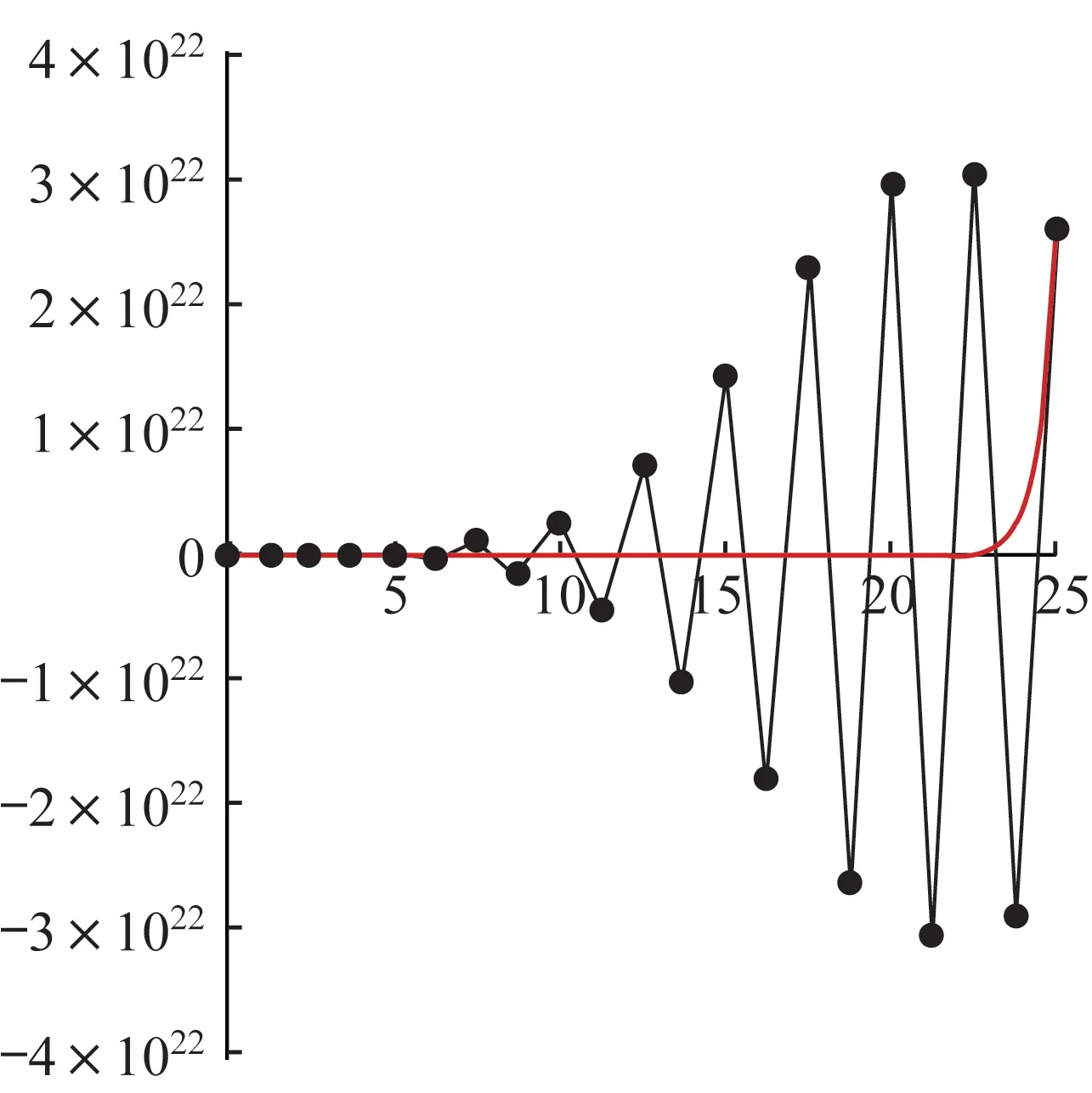
图1 Wilkinson 多项式的形状Fig.1 The plots of Wilkinson polynomial

表10 例4 中M1在3 个子区间内的逼近误差Table 10 The approximation errors of M1 in the three sub-intervals of example 4
4 结 论
提出了一种基于RBM 的高效求根方法,用于计算光滑函数在给定区间的实根。提供了一种能找到重新参数化函数的简单方法,实现渐进式逼近精确实根。与渐进法M2和M3相比,本文方法M1具有与之相同的收敛阶、更高的计算效率。与类牛顿法N2和N3相比,在相同的FE 下,本文方法M1的计算时间与之相近,逼近误差更小、收敛阶更高、计算稳定性更高。结合裁剪法C2和C3的优点(可以隔离给定区间内多项式的所有实根),M1可用于计算给定函数在某给定区间内的所有实根,并具有更高的计算效率和更高的收敛阶。
未来的工作,包括进一步扩展RBM,选取合适的初始值,并将其应用于非线性方程或方程组的求根。
感谢匿名专家对本文的审理和提供的宝贵意见!
