On the spectrum of a new join of two graphs
2021-03-23LIUJianpingWUXianzhangCHENJinsong
LIU Jianping,WU Xianzhang,CHEN Jinsong
(College of Mathematics and Computer Science, Fuzhou University, Fuzhou 350116, China)
Abstract:Given graphs G1 and G2,let E(G1)={e1,e2,…,em1} be the edge set of G1,the graph G1⊙G2 can be obtained from one copy of G1 and m1 copies of G2 by adding a new vertex corresponding to each edge of G1, letting the resulting new vertex set be U={u1,u2,…,um1}, and joining ui with each vertex of i-th copy of G2 and with the endpoints of ei,for i=1,2,…,m1.We can determine: (i) the adjacency spectrum of G1⊙G2 for G1,G2 are both regular graphs, or G1 is regular graph, but G2 is a complete bipartite graph; (ii) the Laplacian spectrum of G1⊙G2 when G1 is a regular graph and G2 is an arbitrary graph; (iii) the signless Laplacian spectrum of G1⊙G2 for both G1 and G2 are regular graphs.As applications, we construct infinitely many pairs of A-cospectral graphs, L-cospectral graphs and Q-cospectral graphs.and determine the number of spanning trees and the Kirchhoff index of G1⊙G2,where G1 is a regular graph.
Key Words: spectrum;cospectral graphs;spanning trees;Kirchhoff index
0 Introduction
All graphs described in this paper are simple and undirect.LetGbe a connected graph with vertex setV(G)={v1,v2,…,vn} and edge setE(G)={e1,e2,…,em}.The adjacency matrix ofGisA(G)=(aij)n×n,withaij=1 ifviis adjacent tovj,andaij=0 otherwise.LetD(G)=diag(d1,d2,…,dn) be the diagonal matrix of vertex degrees ofG.The Laplacian matrix and the signless Laplacian matrix are defined asL(G)=D(G)−A(G) andQ(G)=D(G)+A(G),respectively.The characteristic polynomial ofA(G) is defined asfG(A:x)=det(xEn−A),whereEnis the identity matrix of ordern.The roots offG(A:x)=0 is called the eigenvalues ofG.The eigenvalues ofL(G) andQ(G) are called the Laplacian eigenvalues and the signless Laplacian eigenvalues (in short,L-eigenvalues orQeigenvalues) ofG, respectively.SinceA(G),L(G)andQ(G) are real symmetric matrices, their eigenvalues are all real numbers.Their eigenvalues are conventionally denoted and arranged asλ1(G)≥λ2(G)≥…≥λn(G),μ1(G)≥μ2(G)≥…≥μn(G)andγ1(G)≥γ2(G)≥…≥γn(G),respectively.The set of all the eigenvalues (L-eigenvalues orQeigenvalues) together with their multiplicities is called the spectrum (L-spectrum orQ-spectrum) ofG.GraphsG1andG2are calledA-cospectral (Lcospectra orQ-cospectral) if they have the same adjacency spectrum (L-spectrum orQ-spectrum).The incidence matrixR(G) ofGis a (0,1) matrix with rows indexed by vertices and column indexed by edges,whereRve=1 when the vertex is an endpoint of the edge,and 0 otherwise.Undefined terminology and notations may refer to paper [1].
Spectral graph theory is a fast growing branch of algebraic graph theory and it concerns an interwind tale of properties of graphs and spectrum of related matrices.Calculating the spectra of graphs as well as formulating the characteristic polynomials of graphs is a fundamental and very meaningful work in spectra graph theory.The characteristic polynomial and spectra of graphs help to investigate some properties of graphs such as energy[2-3],the Kirchhoff index[4-6],the Laplacian-energy-like invarients[7-8]and so on.Until now,many graph operations such as the disjoint union,the corona,the edge corona and the neighbour corona have been introduced,and their spectrum are computed[9-15].For more results on spectral graph theory,see paper[16-17].
In this paper,we define a new join of two graphs and determine the following:
The adjacency spectrum ofG1⊙G2forG1,G2are regular graphs,and for a regular graphG1and a complete bipartite graphG2; the Laplacian spectrum ofG1⊙G2for a regular graphG1and an arbitrary graphG2; and the signless Laplacian spectrum ofG1⊙G2forG1,G2are regular graphs.
As applications, we construct infinitely many pairs ofA-cospectral graphs,L-cospectral graphs andQ-cospectral graphs.Moreover, the number of spanning trees and the Kirchhoff index ofG1⊙G2are determined,whereG1is a regular graph.
1 Preliminaries
In this section, we define a new join of two graphsG1andG2and list some known results for later use.
Definition 1Given graphsG1andG2withn1,n2vertices respectively, letE(G1)={e1,e2,…,em1} be the edge set ofG1,the graphG1⊙G2can be obtained from one copy ofG1andm1copies ofG2as follows.Firstly, we add a new vertex corresponding to each edge ofG1, the resulting new vertex setU={u1,u2,…,um1}.Then joinuiwith each vertex ofi-th copy ofG2and with the endpoints ofei, fori=1,2,…,m1.
Note that the graphG1⊙G2in definition 1 containsn1+m1(n2+1) vertices.Consider the graphsG1=C4,G2=P3.Fig.1 describes the graphC4⊙P3.
The symbols 0nand 1n(resp.,0m×nand 1m×n)denote the length-ncolumn vectors (resp.,m×nmatrices) consisting entirely of 0′s and 1′s respectively.The ΓA(x) of the square matrixAis defined to be the sum of entries of the matrix (xEn−A)−1[14].This can be calculated as ΓA(x)= 1T(xEn−A)−11.The Kronecker productA⊗Bof two matricesA=(aij)m×nandB=(bij)p×qis themp×nqmatrix which obtained fromAby replacing each elementaijbyaij B.
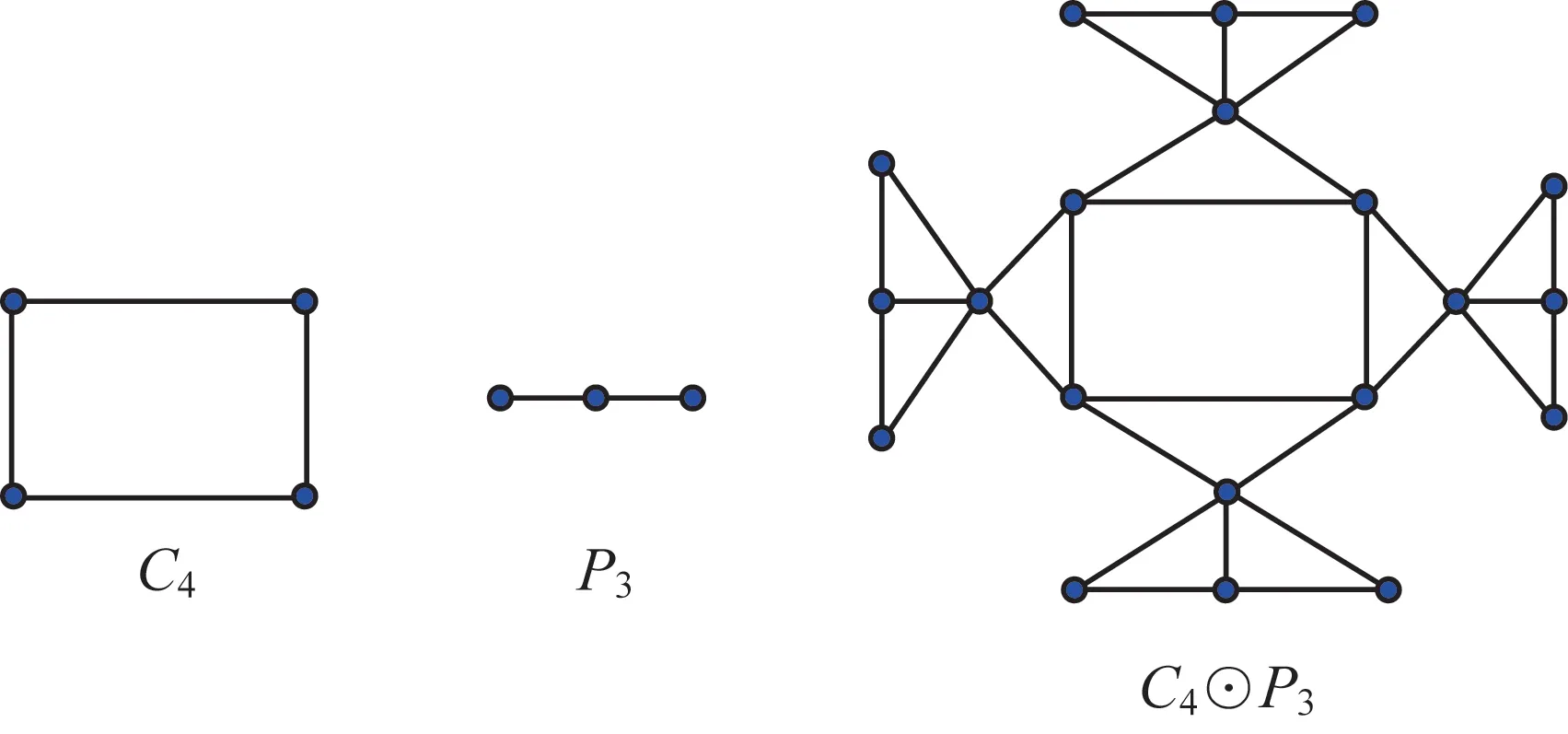
Fig.1 Graph C4⊙P3
Lemma 1[18]LetA,B,C,Dbe four arbitrary matrices, then the Kronecker product has the following properties:
(i) If the productsACandBDexist, then(A⊗B)T=AT⊗BTand (A⊗B)(C⊗D) =AC⊗BD,
(ii) IfAandBare nonsingular matrices, then(A⊗B)−1=A−1⊗B−1,
(iii) IfAandBare square matrices of ordernandp,then det(A⊗B) =(detA)p(detB)n.
Lemma 2[19]LetGbe anr-regular graph withnvertices andmedges,and letA,Rbe its adjacency matrix and incidence matrix, respectively, thenRRT=A+rEnandRTR=A(GL)+2Em, whereGLis the line graph ofG.
Lemma 3[20]LetM1,M2,M3,M4bep×p, p×q,q×p,q×qmatrix, respectively, withM1andM4are invertible,then
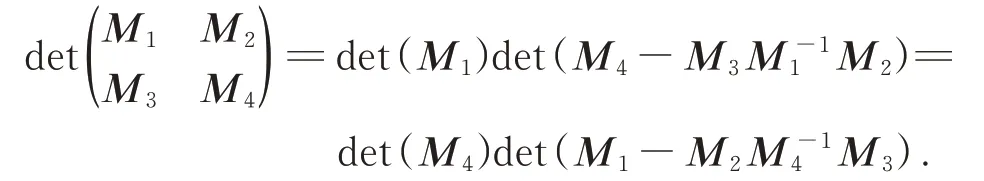
Lemma 4[14]LetGber-regular withnvertices and letAbe the adjacency matrix ofG,then

Lemma 5[14]LetGbe the complete bipartite graphKp,qand letAbe the adjacency matrix ofG,then
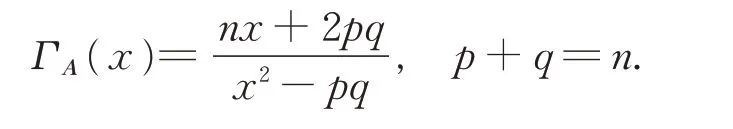
2 Spectrum of the graph G1⊙G2
In this section,motivated by the above works,we determine the adjacency spectrum,the Laplacian spectrum and the signless Laplacian spectrum ofG1⊙G2.
2.1 Adjacency spectrum of the graph G1⊙G2
In this subsection,we present the characteristic polynomial and the adjacency spectrum ofG1⊙G2forG1,G2are regular graphs,and for a regular graphG1and a complete bipartite graphG2.Moreover, we construct infinitely many pairs ofA-cospectral graphs.
Theorem 1LetGibe anri-regular withnivertices andmiedges,and letAi,Ribe the adjacency matrix and incidence matrix ofGifori=1,2,respectively.Then the characteristic polynomial of the adjacency matrixAofG1⊙G2is

ProofBy a proper labelling of vertices, the adjacency matrixAofG1⊙G2can be written as
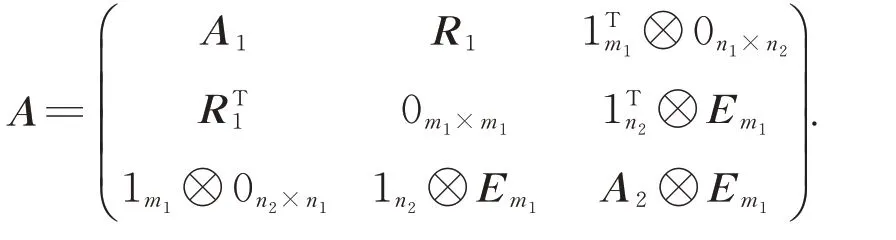
It follows that the characteristic polynomial ofG1⊙G2is
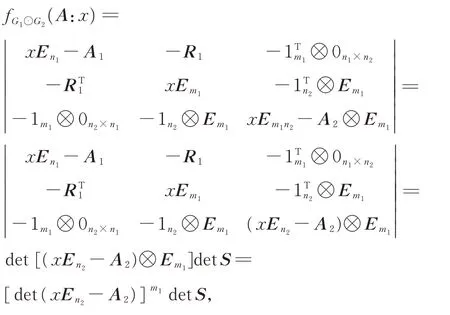
where
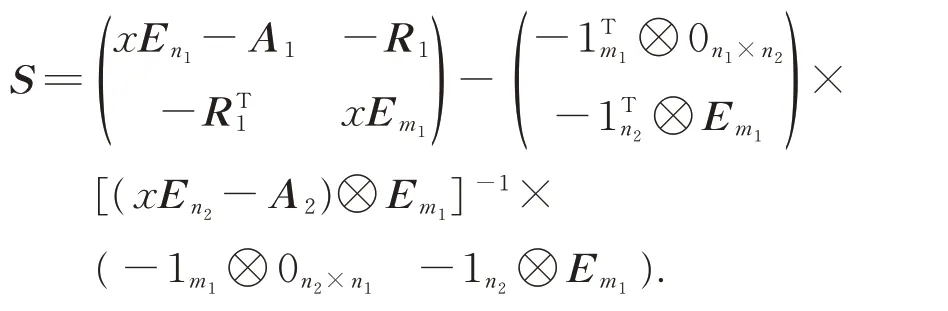
By the Kronecker product properties,we have

thus,we have

then we get
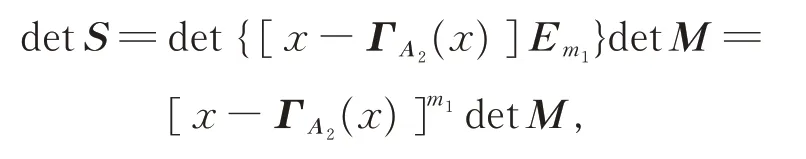
where

then,we get
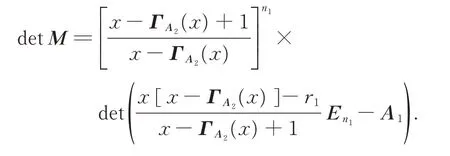
It follows from the above argument,
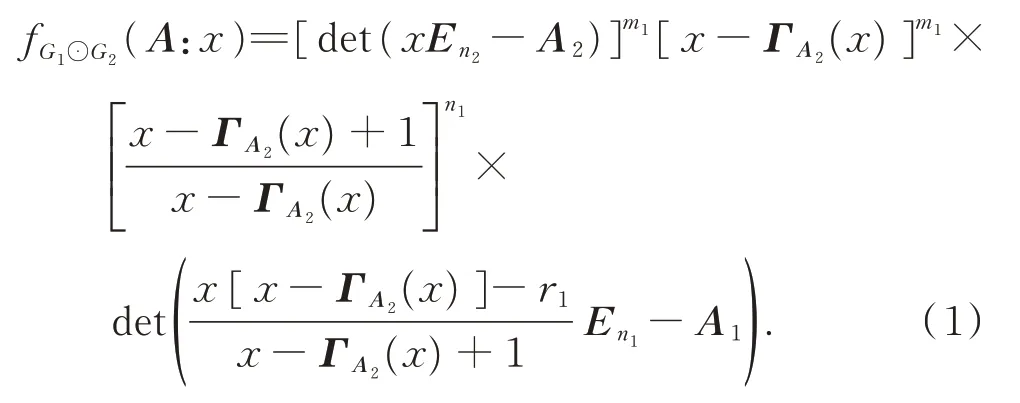

Directly from theorem 1,we have the following corollary.
Corollary 1LetGibe anri-regular withnivertices andmiedges,letAibe the adjacency matrix ofGi,wherei=1,2.Then the adjacency spectrum ofG1⊙G2consists of
(i)λi(A2),repeatedm1times fori=2,3,…,n2.
(iii)Three roots of
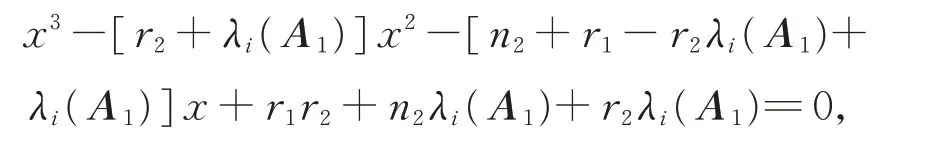
fori=1,2,…,n1.
Theorem 2LetGbe anr1-regular withn1vertices andm1edges,letKp,qbe a complete bipartite graph withn2=p+qvertices, and letA,A1,A2be the adjacency matrix ofG⊙Kp,q,G,andKp,q,respectively,then
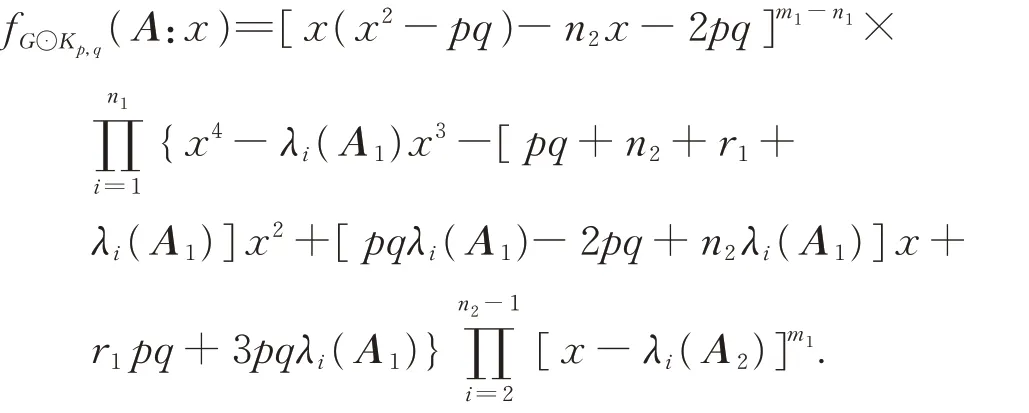
ProofBy equation (1), we have
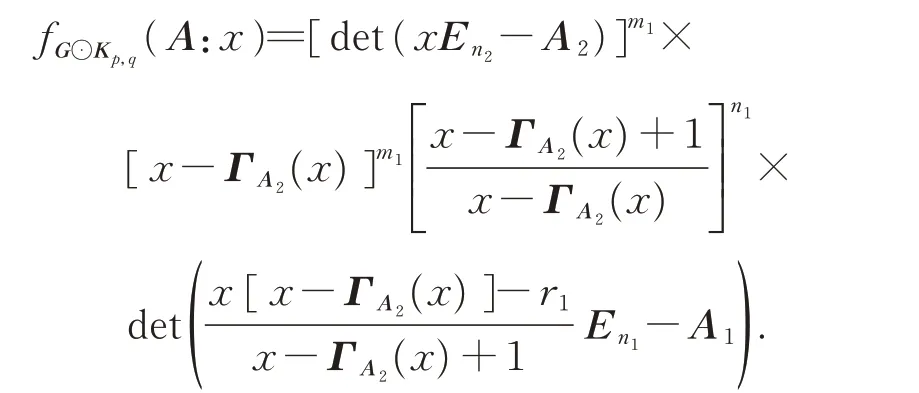


SinceA2has eigenvalueswith multiplicity one, we yield the following equations:

Directly from theorem 2, we have the following corollaries.
Corollary 2LetGbe anr1-regular withn1vertices andm1edges,Kp,qbe a complete bipartite graph withn2vertices,and letA1,A2be the adjacency matrix ofGandKp,q,respectively,then the adjacency spectrum ofG⊙Kp,qconsists of
(i)λi(A2), repeatedm1times fori=2,3,…,n2−1.
(ii) Three roots ofx(x2−pq)−n2x−2pq=0,each root repeatedm1−n1times.
(iii)Four roots of
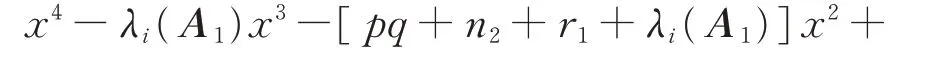

Corollary 3IfGis anr-regular graph,H1andH2areA-cospectral graphs withΓA(H1)(x) =ΓA(H2)(x), thenG⊙H1andG⊙H2areA-cospectral graphs.
ProofBy equation (1),we have
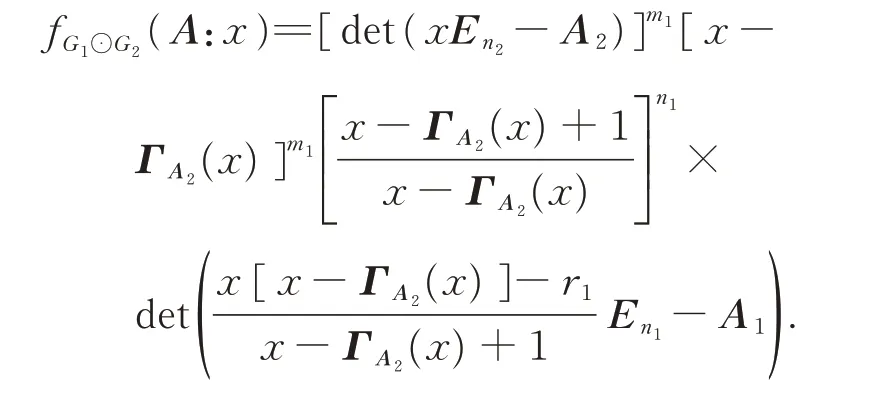
IfΓA(H1)(x) =ΓA(H2)(x), then

Hence,G⊙H1andG⊙H2areA-cospectral graphs.
2.2 Laplacian spectrum of the graph G1⊙G2
In this subsection, we present the Laplacian characteristic polynomial and the Laplacian spectrum of the graphG1⊙G2,whereG1is a regular andG2is an arbitrary graph.Moreover, many pairs ofLcospectral graphs are constructed infinitely,also the number of spanning trees and the Kirchhoff index ofG1⊙G2for a regular graphG1are determined.
Theorem 3LetG1be anr1-regular withn1vertices andm1edges,G2be an arbitrary graph withn2vertices andm2edges,and letLi,Ribe the Laplacian matrix and incidence matrix ofGifori=1,2,respectively,then

ProofThe Laplacian matrixLofG1⊙G2can be written as
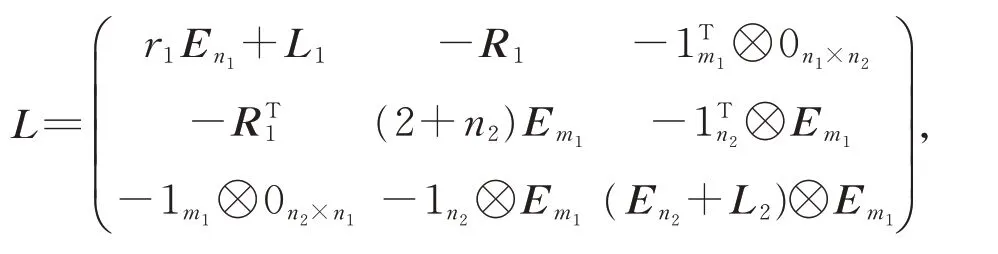
then the Laplacian characteristic polynomial ofG1⊙G2is
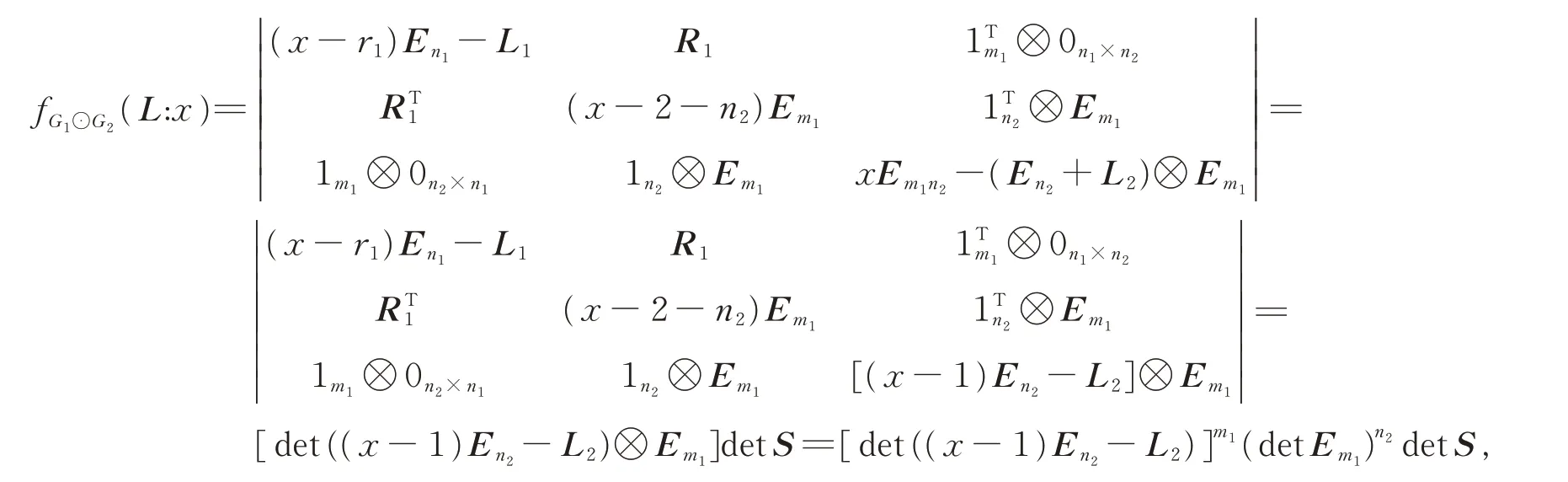
where
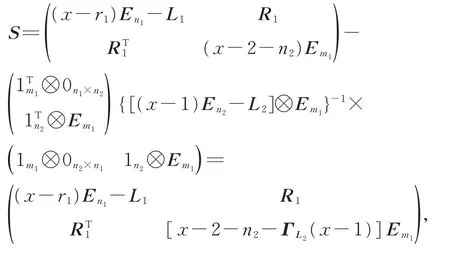
thus,
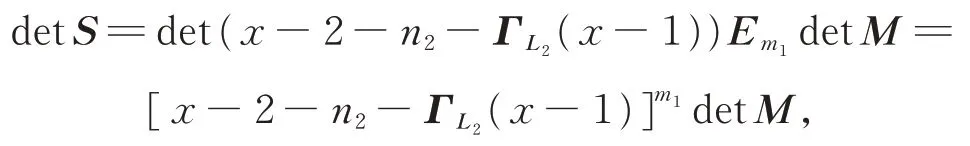
where
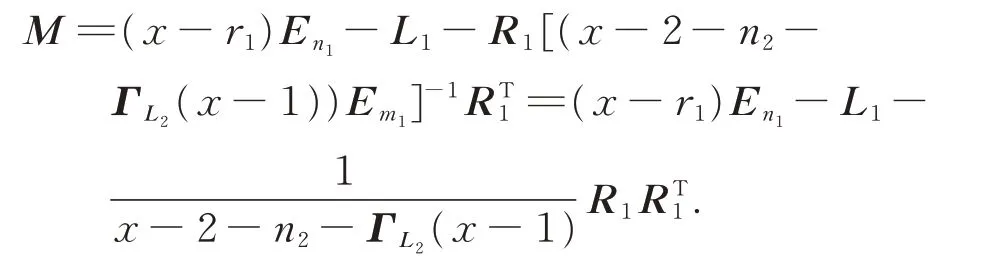
SinceG1isr1-regular,2r1En1,thus,we have
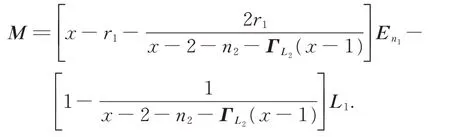
then,we get

It follows from above argument,


Since the Laplacian matrix ofG2has a constant row sum 0,we have.By direct calculation,we obtain
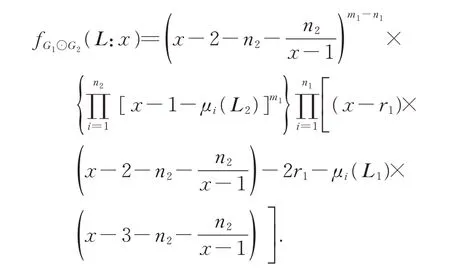
SinceL2has an eigenvalue 0,thus
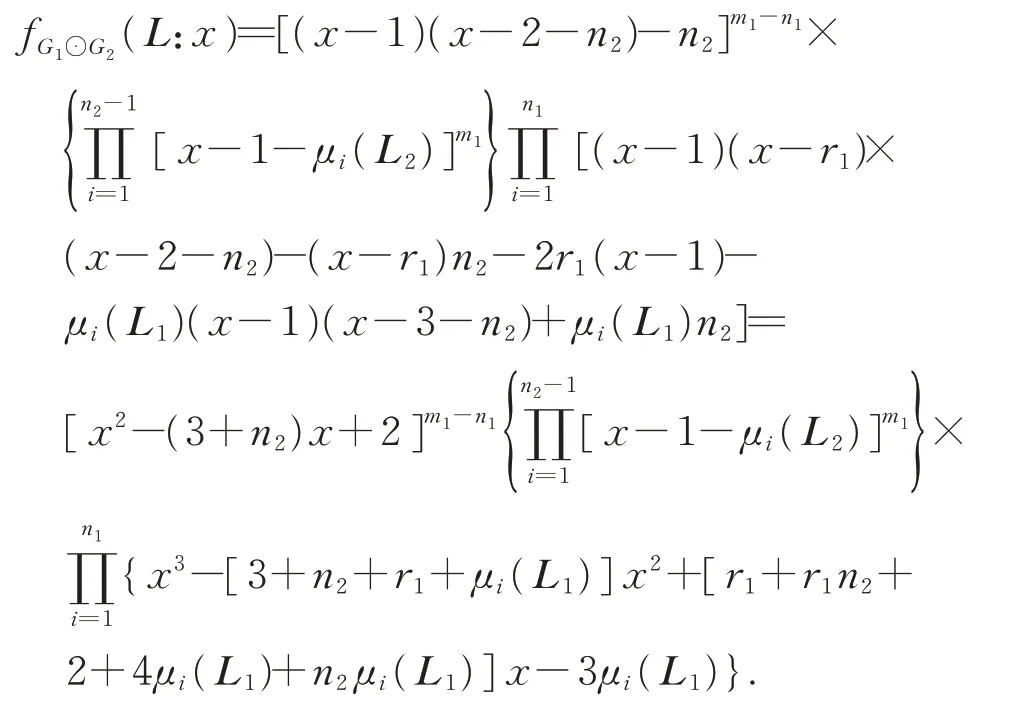
Immediately from theorem 3, we have the following corollaries.
Corollary 4LetG1be anr1-regular withn1vertices andm1edges,G2be an arbitrary graph withn2vertices andm2edges,and letLibe the Laplacian matrix ofGifori=1,2, respectively.Then the Laplacian spectrum ofG1⊙G2consists of
(i) 1+μi(L2), repeatedm1times fori=1,2,…,n2−1.
(iii)Three roots of
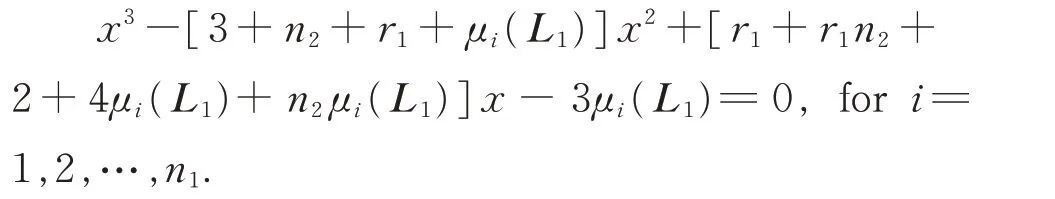
Corollary 5IfGis anr-regular graph,andH1andH2areL-cospectral graphs withΓL(H1)(x−1)=ΓL(H2)(x−1), thenG⊙H1andG⊙H2areLcospectral graphs.
ProofBy equation (2),we have
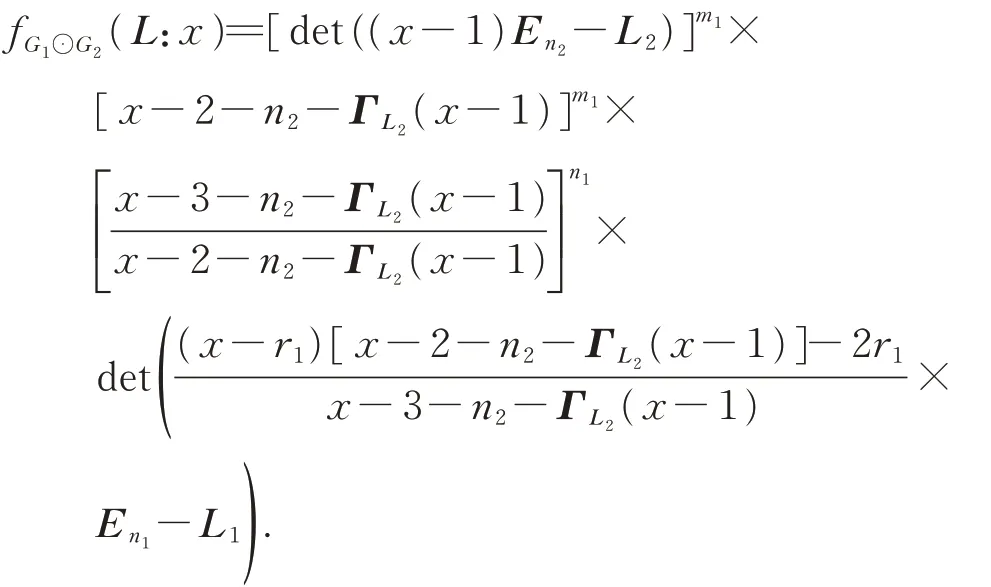
then
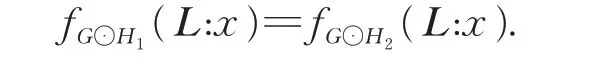
Hence,G⊙H1andG⊙H2areL-cospectral graphs.
From the matrix-tree theorem[21],the number of spanning trees of a connected graphGwithnvertices is
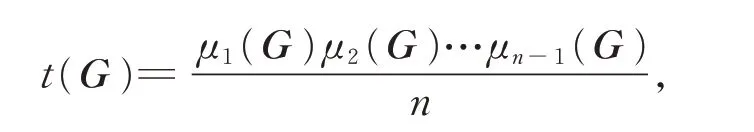
whereμ1(G),μ2(G),…,μn−1(G) are the non-zero Laplacian eigenvalues ofG.Recall thatμ1(G)μ2(G)…μn−1(G) is equal to the absolute value of the coefficient ofxin polynomialfG(L:x).As an application of theorem 3, we present the number of spanning trees for
Corollary 6LetG1be anr1-regular graph withn1vertices andm1edges,G2be an arbitrary graph withn2vertices andm2edges,and letLibe the Laplacian matrix ofGifori=1,2,respectively.Then
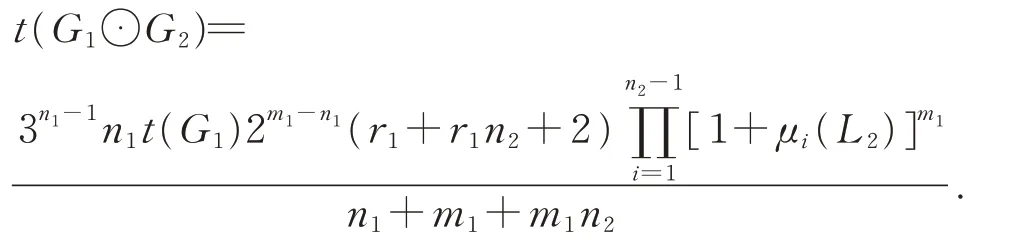
ProofUsing theorem 3 and the matrix-tree theorem,notice thatt(G1⊙G2) is a positive integer,we obtain
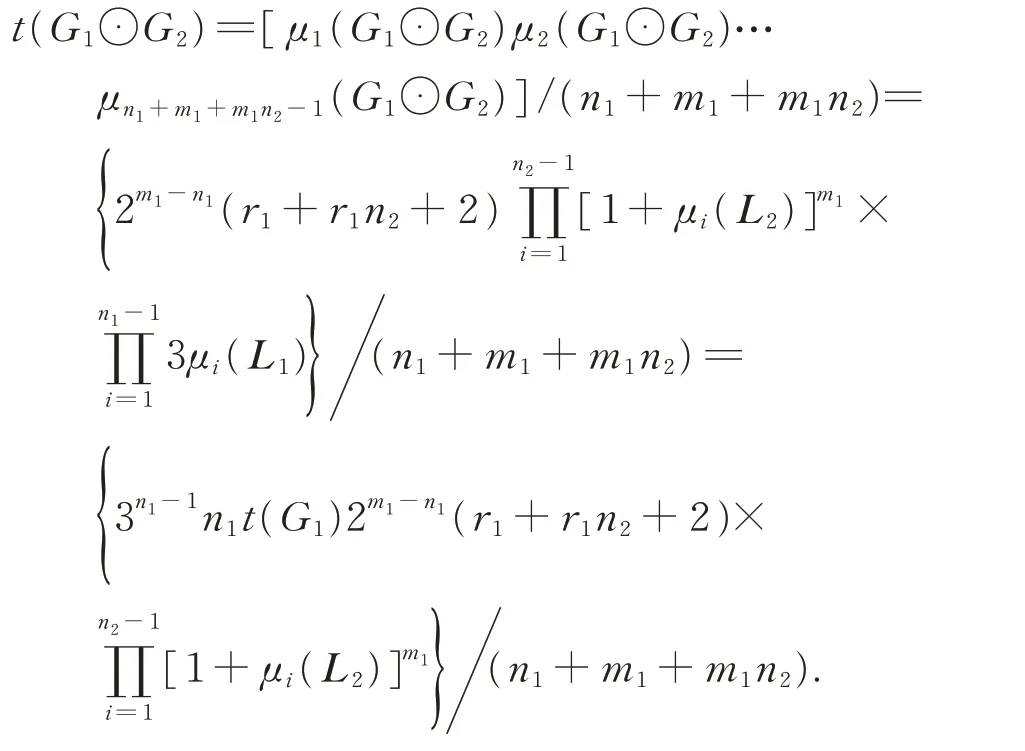
The Kirchhoff index of a graphG,denoted byKf(G),is defined as the sum of resistance distances between all pairs of vertices[15,22].At almost exactly the same time,GUTMAN et al[23]and ZHU et al[24]proved that the Kirchhoff index of a connected graphGwithn(n≥2)vertices can be expressed as
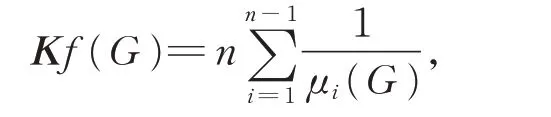
whereμ1(G),μ2(G),…,μn−1(G) are the non-zero Laplacian eigenvalues ofG.
Now we consider the Kirchhoff index of the graphG1⊙G2.
Corollary 7LetG1be anr1-regular connected graph withn1vertices andm1edges,G2be an arbitrary graph withn2vertices andm2edges,and letLibe the Laplacian matrix ofGifori=1,2,respectively.Then
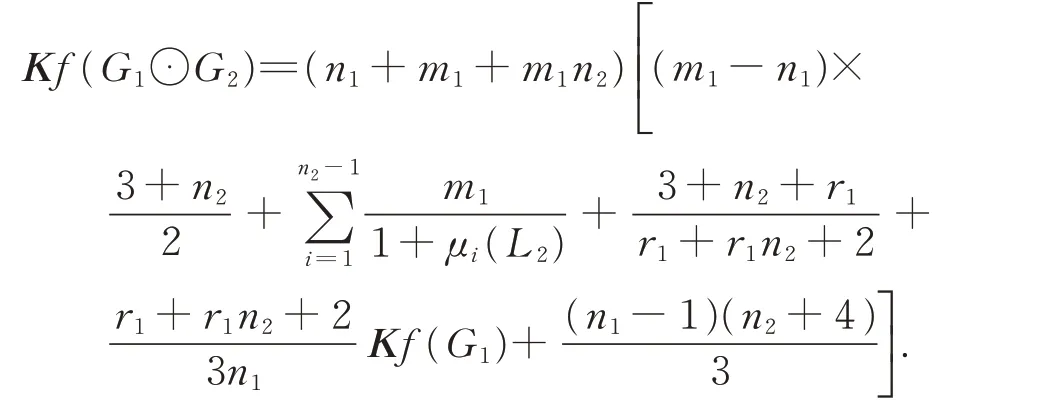
ProofRecall thatG1⊙G2hasn1+m1+m1n2vertices.By theorem 3,we obtain

2.3 Signless Laplacian spectrum of the graph G1⊙G2
Now we consider the signless Laplacian characteristic polynomial and the signless Laplacian spectrum ofG1⊙G2forG1andG2are regular graphs.Furthermore,we construct infinitely many pairs ofQcospectral graphs.
Theorem 4Fori=1,2, letGibe anri-regular withnivertices andmiedges,and letQi,Ribe the signless Laplacian matrix and incidence matrix ofGi,respectively.Then,
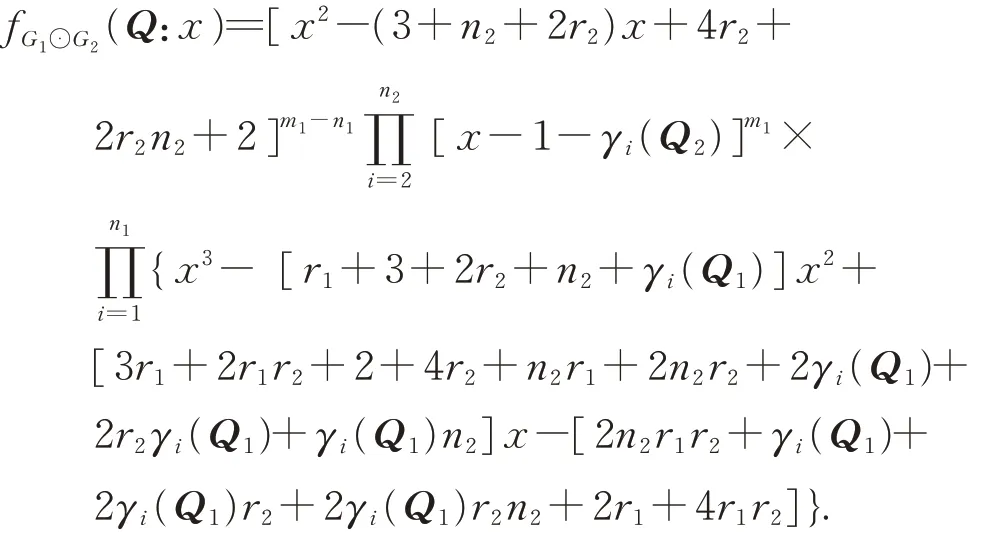
ProofThe signless Laplacian matrixQofG1⊙G2can be written as

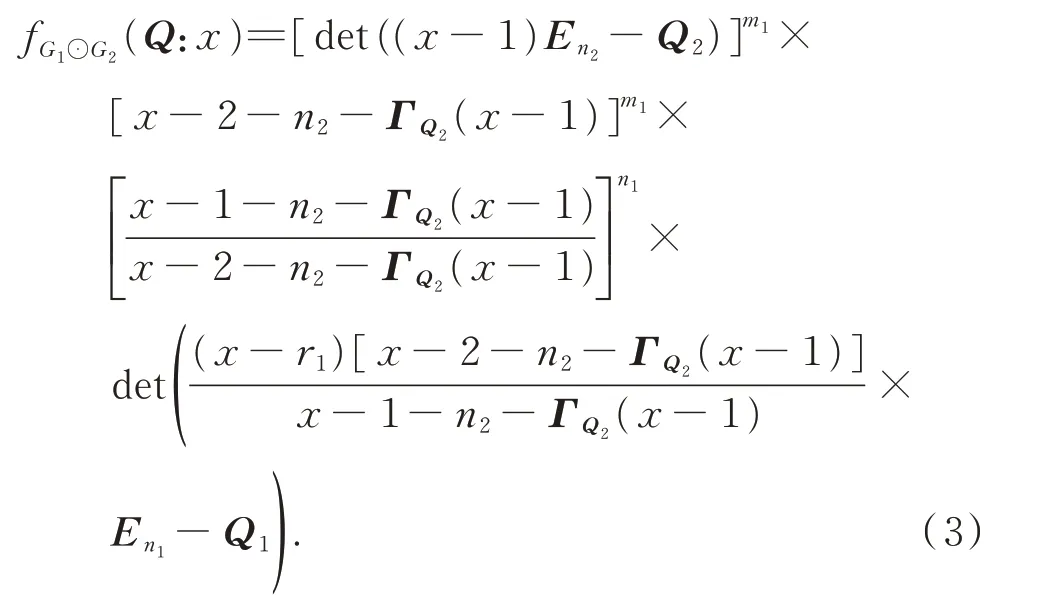
SinceG2isr2-regular,Q2has a constant row sum 2r2,thusBy direct calculation,we obtain that
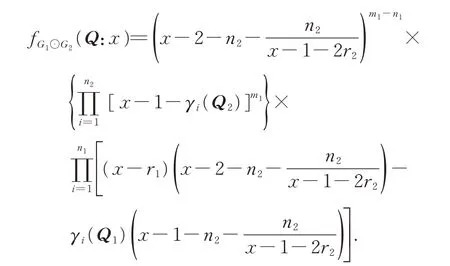
SinceQ2has an eigenvalue 2r2,which yields the following equations:
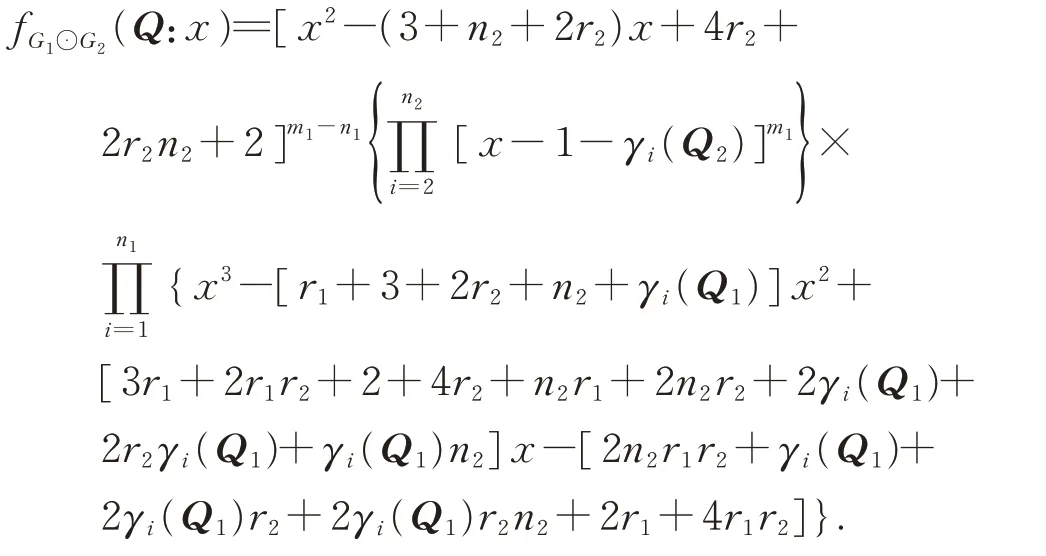
Directly from theorem 4,we have the following corollaries.
Corollary 8LetGibe anri-regular withnivertices andmiedges fori=1,2.Then the signless Laplacian spectrum ofG1⊙G2consists of
(i) 1+γi(Q2), repeatedm1times fori=2,3,…,n2.
(iii)Three roots of
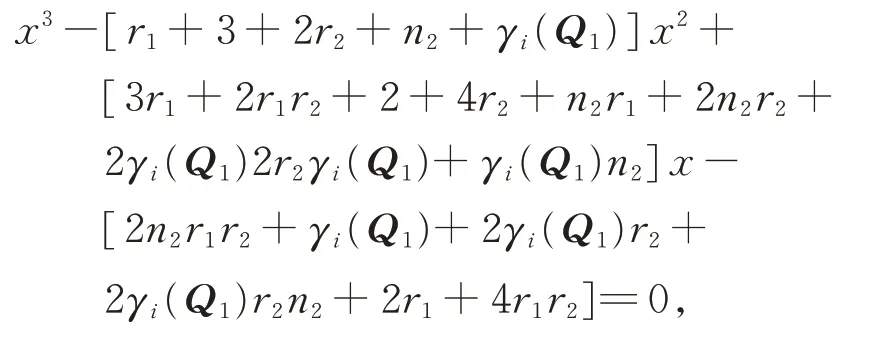
fori=1,2,…,n1.
Corollary 9IfGis anr-regular graph,andH1andH2are theQ-cospectral graphs withΓQ(H1)(x−1)=ΓQ(H2)(x−1).ThenG⊙H1andG⊙H2areQ-cospectral graphs.
ProofBy equation (3),we have
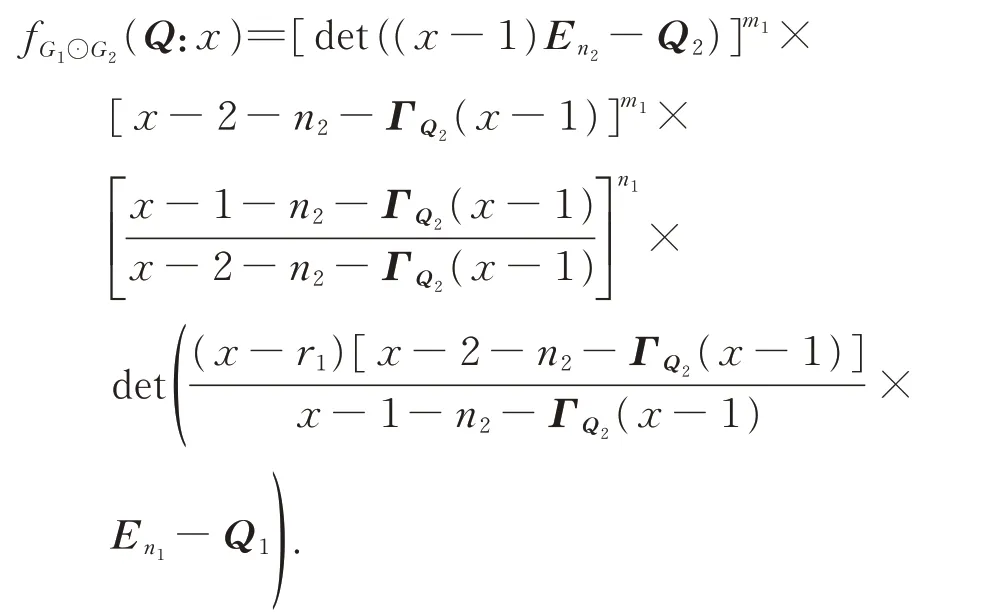
IfΓQ(H1)(x−1)=ΓQ(H2)(x−1),then
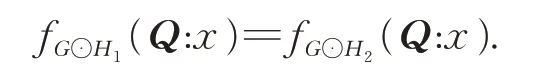
Hence,G⊙H1andG⊙H2areQ-cospectral graphs.
