砂卵石地层不同结构型式大跨无柱地铁车站的抗震动力响应分析

李岩龙

(1.中铁第一勘察设计院集团有限公司， 710043， 西安； 2.陕西省铁道及地下交通工程重点实验室， 710043， 西安∥工程师)

地铁车站设计方案已日趋成熟。无柱车站的出现，实现了车站舒适、实用、美观的协调统一[1-3]。在进行结构设计时，因无柱车站缺少框架梁等耗能构件，加上砂卵石地层条件下地震特性的离散性，车站的抗震性能分析显得尤为重要[4-5]。国内最先采用无柱结构的车站是站台宽达8 m的上海轨道交通1号线衡山路站。随后广州地铁2号线、上海轨道交通7号线、深圳地铁9号线也相继建有无柱车站。上述无柱车站均采用矩形平顶直墙结构，结构标准段净宽小于16.25 m。相比于有柱车站，无柱车站增加了构件截面尺寸，尚可满足结构受力的要求。但随着客流日趋增长，部分线路设计时采用了12 m宽站台及A型列车，导致车站标准段的净宽达19.7 m。

根据《建筑抗震设计规范》，18 m以上的结构属大跨结构。考虑到工程经济性及大体积混凝土浇筑等诸多问题，对于大跨结构不建议采取无限增厚截面的方式，拱形车站的出现较好地解决了这一问题。

目前，国内外学者针对地下大跨地铁车站抗震展开了大量研究，并已取得显著成果[4-6]。然而，既有研究对不同结构型式大跨无柱车站的抗震响应对比分析却鲜有报道，尤其是因拱形结构不同的矢跨比导致车站结构内力、位移、层间位移角及相对位移时程曲线发生显著变化的报道更少。因此，本文在既有9 m宽站台无柱车站抗震分析研究的基础上，对比分析不同结构型式大跨无柱车站的受力特点、内力变化规律及结构抗震动力响应，据此对大跨无柱地铁车站的结构选型提出建议。

1 工程概况

本文依托成都轨道交通某大跨无柱地下车站进行结构抗震动力响应分析。 为对比不同结构型式的动力响应，设计了4种结构型式方案：方案1为矩形平顶直墙结构；方案2为折线拱结构，矢跨比为0.15；方案3为三圆拱结构，矢跨比为0.21；方案4为单圆拱结构，矢跨比为0.26。方案2～4的底部仰拱矢跨比均为0.1。各结构型式汇总如表1所示。

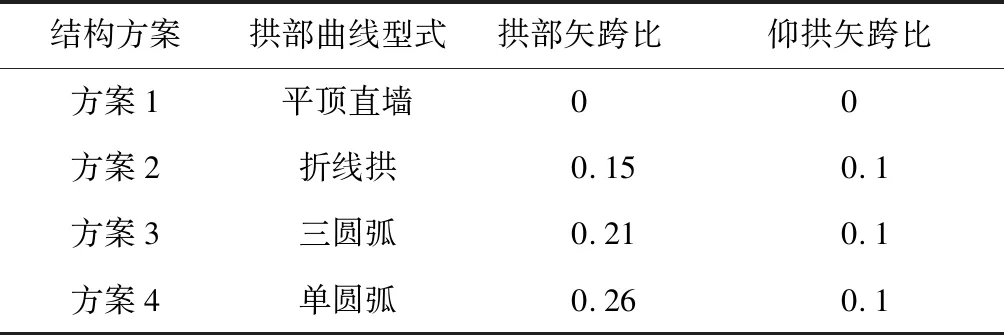
表1 4种结构型式汇总表

将各构件截面尺寸进行统一：顶板取1 300 mm，中板取800 mm，底板取1 400 mm，侧墙取1 300 mm。这4种结构型式站台的宽度均为12 m，结构板跨均为19.7 m，覆土厚度均为4 m。车站断面如图1所示。

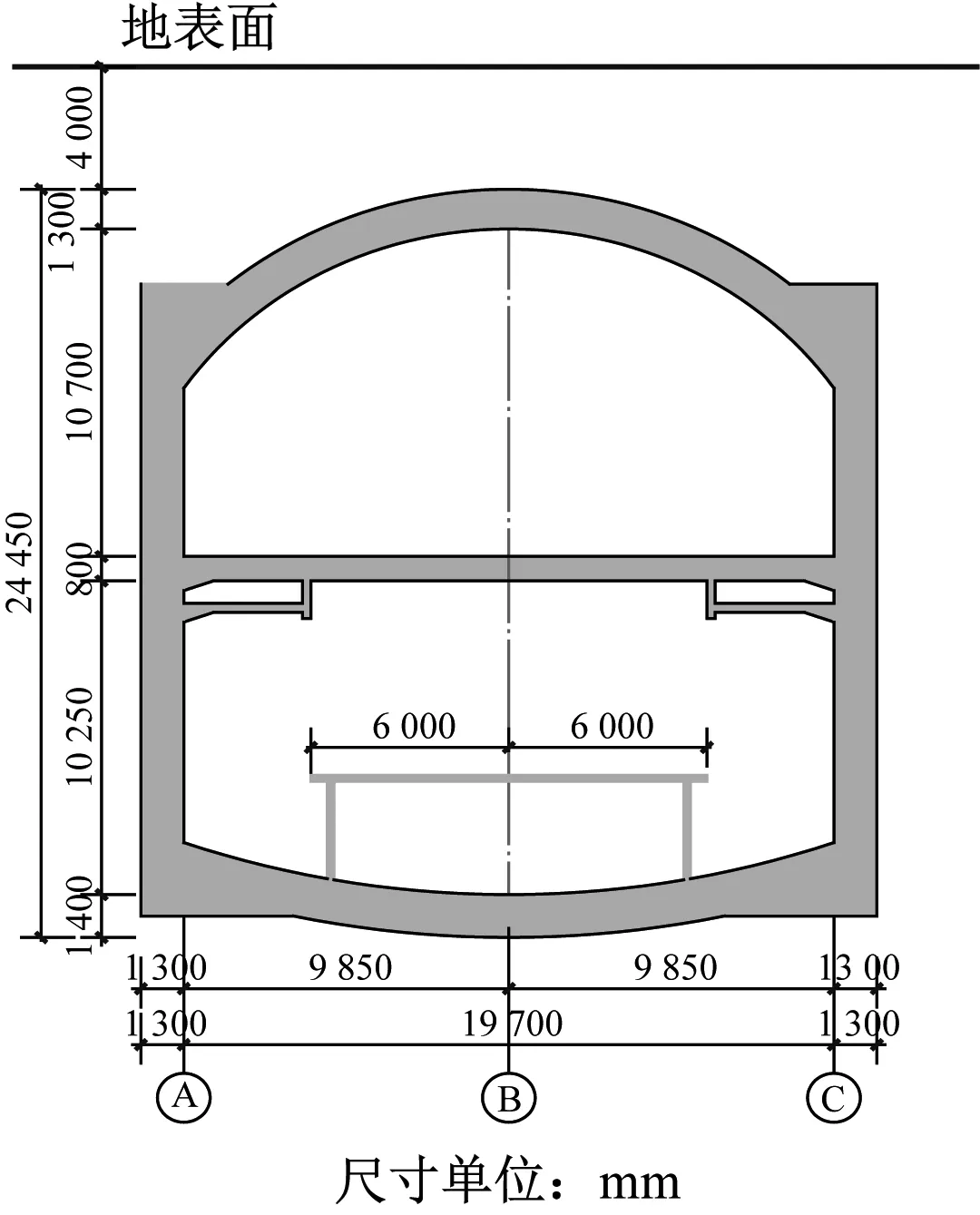
图1 大跨无柱地铁车站典型断面

2 抗震计算数值模拟及对比分析

2.1 抗震计算模型设计

采用有限元分析软件GTS NX对4种不同结构型式无柱车站进行抗震动力响应分析，其典型断面有限元分析模型如图2所示。

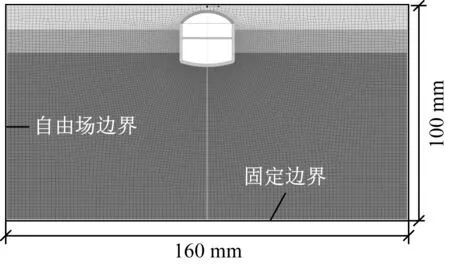
图2 典型断面有限元分析模型

模型采用时程分析法进行抗震动力响应计算[9-11]。边界采用人工边界进行处理[12]，根据《城市轨道交通结构抗震设计规范》[13]，人工边界宽度取结构有效宽度的3倍，底部采用固定边界，设计地震作用基准面取在场地覆盖土层70 m深度土层位置。土体采用Mohr-Coulomb本构模型进行平面应变单元模拟。结构采用线弹性本构模型、Beam梁单元模拟。土体与结构单元间通过节点耦合连接。动力计算采用瑞利型力学阻尼，阻尼矩阵C与质量矩阵M和刚度矩阵K的关系为：

C=αM+βK

式中：

α，β——分别为与质量和刚度成比例的阻尼常数。

动力时程分析法的计算模型如图3所示。

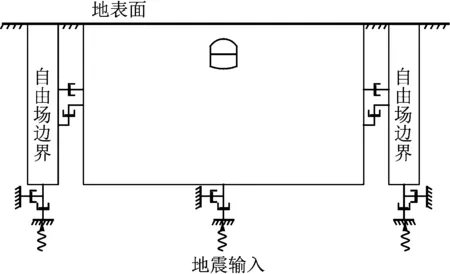
图3 动力时程分析法计算模型

2.2 地震波的选取

该模型选取地震加速度峰值为0.1g的EL-Centro波作为地震动输入，持时12 s，时间步距为0.02 s。地震动入射方向与车站的纵轴垂直，施加地震荷载前通过Seismo Signal软件进行滤波及基线校正。加速度时程曲线及其傅里叶变换如图4所示。

2.3 计算参数的选取

本文选取成都市较为典型的砂卵石地层进行分析。该地层从上之下各土层及车站结构的主要物理力学参数如表2所示。

a) 加速度时程曲线

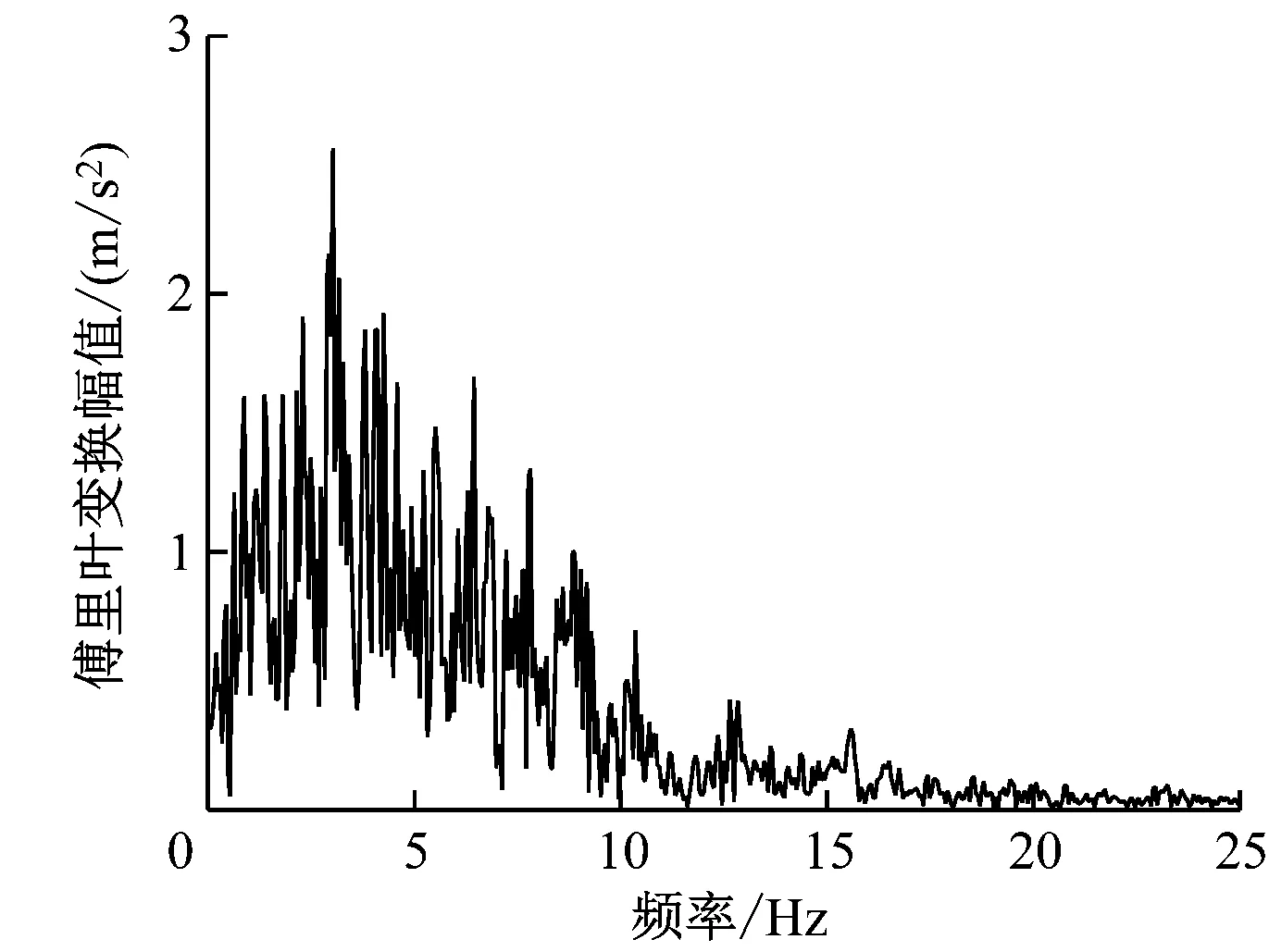
b) 傅里叶变换

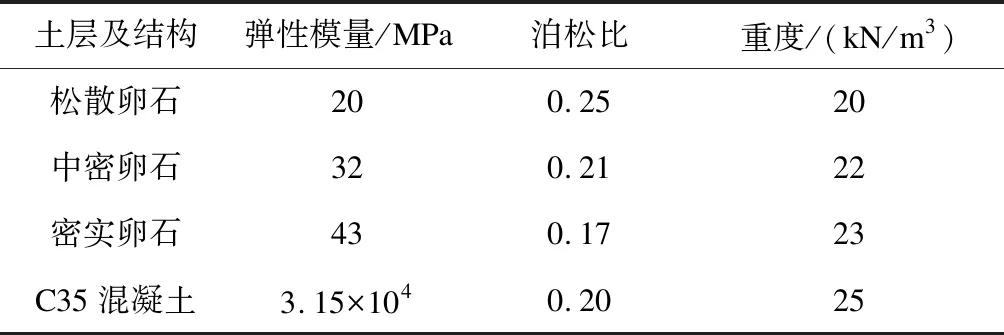
表2 土层与车站结构的主要力学参数表

2.4 不同结构型式无柱车站的抗震动力响应分析

为研究不同结构型式无柱车站在竖向荷载及周围土体侧压力荷载下的结构抗震响应，选取结构顶板、底板发生最大相对位移差时的内力(弯矩、轴力、剪力)及层间位移角等参数进行对比分析。其中，弯矩以结构外侧受拉为正，剪力以使截面顺时针转动为正，轴力以拉力为正。

2.4.1 弯矩计算分析

图5为不同结构型式无柱车站在竖向荷载及周围土体侧压力荷载下的弯矩计算。由图5可知，不同结构型式的车站弯矩大致呈“对角双曲线”形分布，其最大正弯矩出现在结构拱顶与拱肩跨中位置附近，最大负弯矩出现于结构底板与侧墙交界处位置。

由表3可知，与矩形平顶直墙结构的弯矩值相比，折线拱、三圆拱、单圆拱结构在顶板处的弯矩值分别减少了24.4%、31.0%、34.6%，在底板处的弯

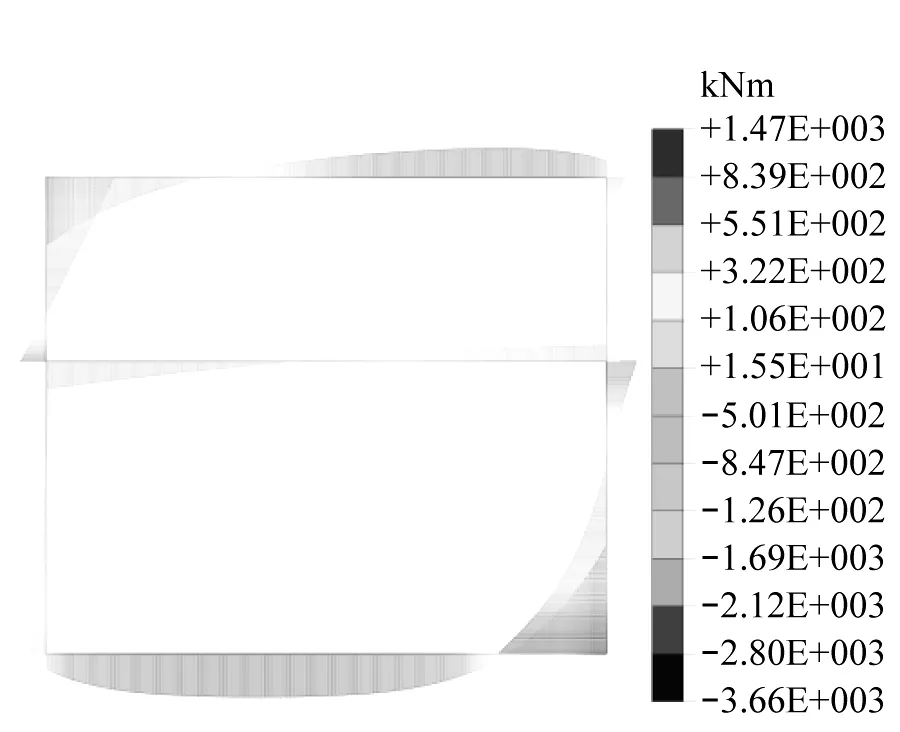
a)平顶直墙

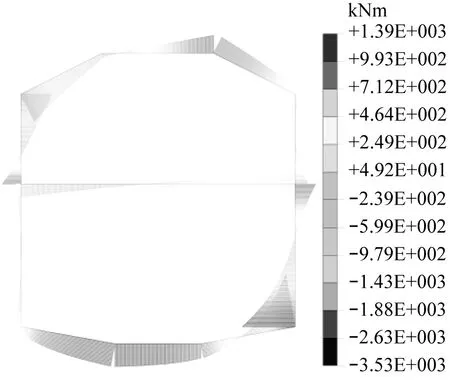
b)折线拱

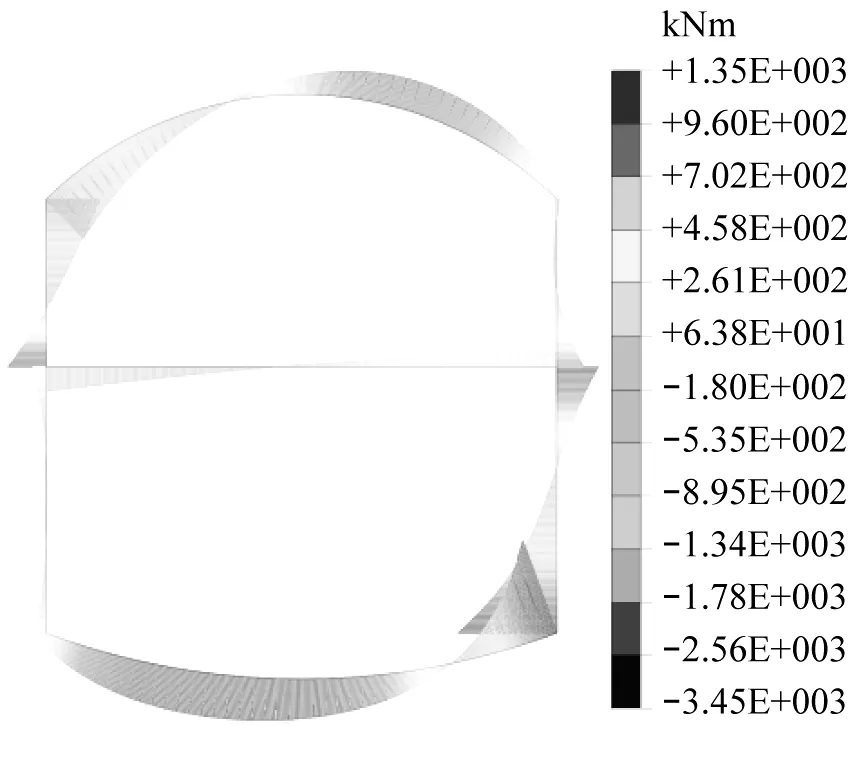
c)三圆拱

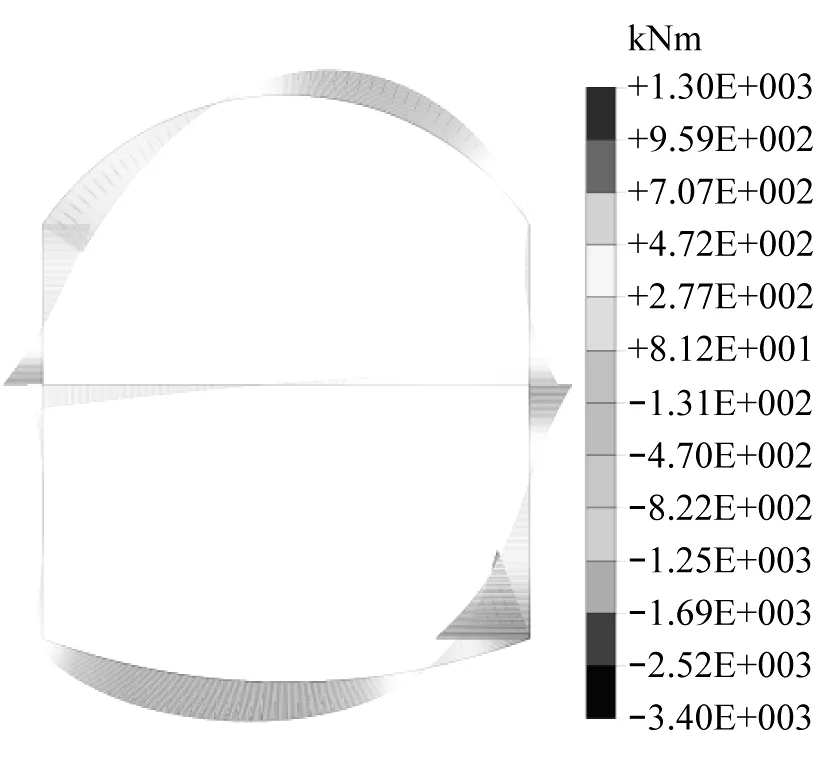
d)单圆拱

矩值分别减少了6.1%、14.0%、14.5%，结构受力得到显著改善。随着结构矢跨比增加，弯矩降幅逐渐趋于平缓。

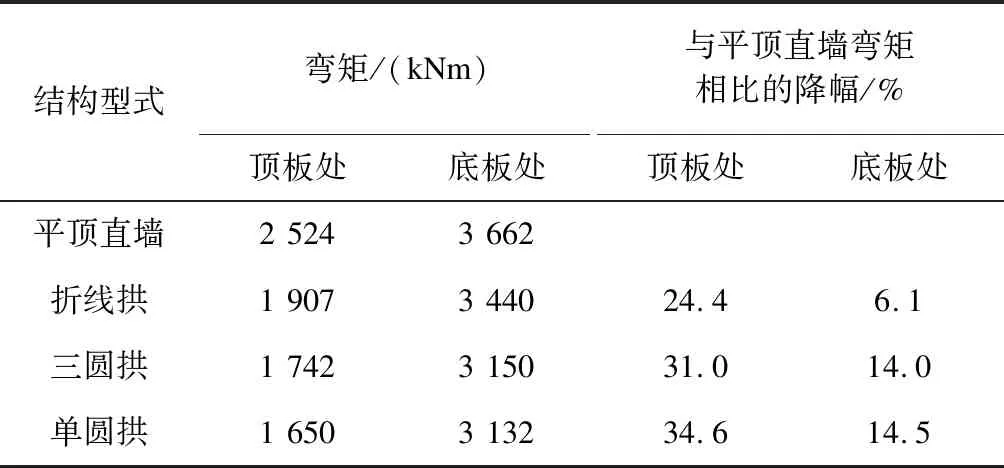
表3 不同结构型式无柱车站顶板和底板处的弯矩值对比

2.4.2 轴力和剪力分析

结构顶板、底板处的轴力和剪力分别如表4、5所示。由表4、5可知，随着结构矢跨比增加，结构顶、底板的轴力逐渐增加，剪力逐渐减少。与矩形平顶直墙结构的轴力相比，折线拱、三圆拱、板单圆拱结构在顶板处轴力分别增大了32.6%、77.0%、84.9%，在底板处轴力分别增大了33.2%、57.6%、60.8%；与矩形平顶直墙结构的剪力相比，折线拱、三圆拱、板单圆拱结构在顶板处剪力分别减少了20.2%、40.5%、50.7%，在底板处剪力分别减少了12.2%、23.8%、25.3%。可见，结构受力得到显著改善。

2.4.3 层间位移面计算分析

图6为不同结构型式下的车站相对位移。根据图6的计算结果，得到不同车站结构层间位移角，如表6所示。由表6可知，随着结构矢跨比增加，相比

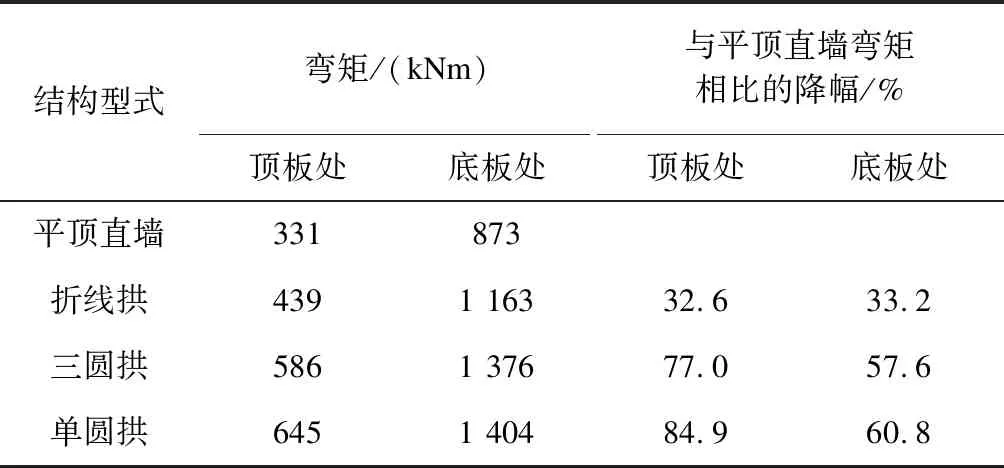
表4 不同结构型式无柱车站顶板和底板处的轴力值对比

表5 不同结构型式无柱车站顶板和底板处的剪力值对比

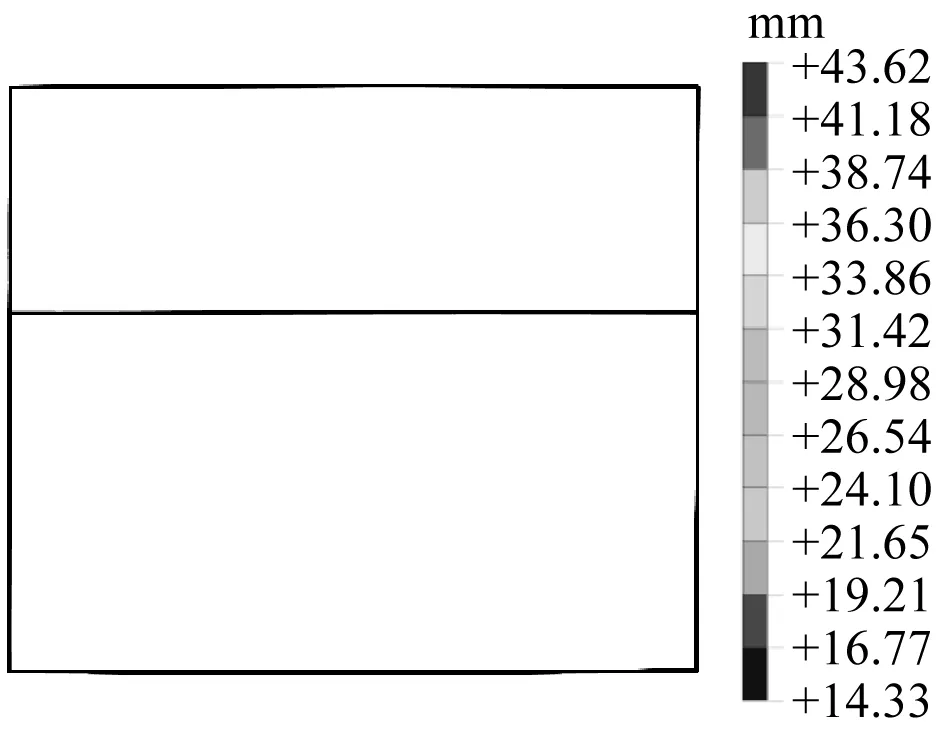
a)平顶直墙

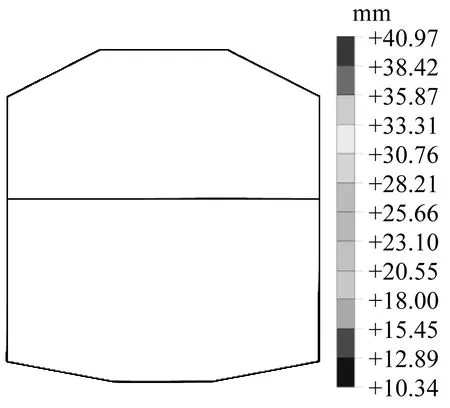
b)折线拱

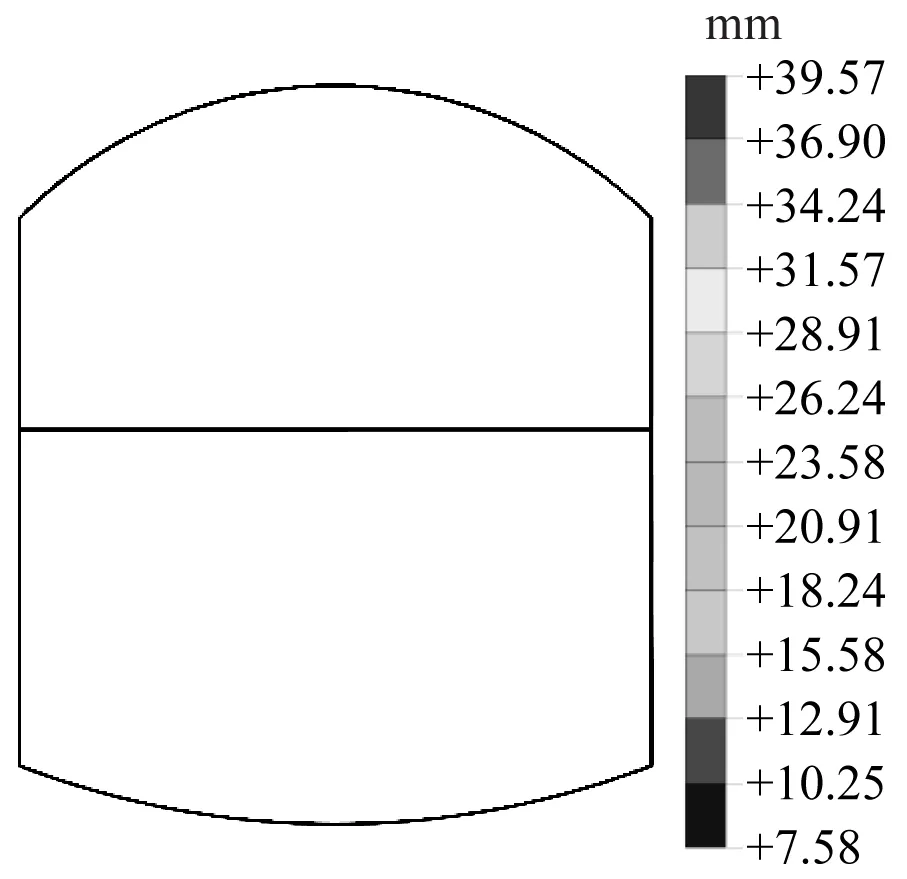
c)三圆拱

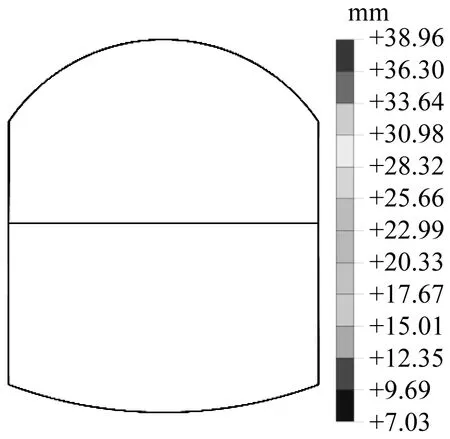
d)单圆拱

于矩形平顶直墙结构的层间位移角，折线拱、三圆拱、单圆拱结构的层间位移角分别减少了21.5%、25.7%及29.4%。

2.4.4 抗震动力响应计算结果分析

为对比拱顶位置不同矢跨比下结构弯矩及层间位移角影响的敏感性，选取折线拱、三圆拱、单圆拱结构的弯矩变化幅度及层间位移角变化幅度进行对比，如图7所示。可见，随着结构矢跨比增大，弯矩及层间位移角变化幅度呈递增趋势。

由上述结构抗震动力响应计算可知：① 在地层

表6 不同结构型式无柱车站的层间位移角值对比

图7 不同结构型式无柱车站的弯矩、层间位移角

及竖向荷载作用下，结构轴力值增幅较为明显，部分竖向荷载通过拱结构转化为轴力，结构顶板弯矩值得以明显改善。② 拱部矢跨比越大，拱顶及拱脚弯矩越小，受力越有利。当矢跨比为0.26时，拱部弯矩可减少约35%。③ 折线拱结构相较平顶直墙结构内力有明显改善，且比曲拱(三圆拱、单圆拱)结构相较折线拱结构的内力改善更为显著。随着结构矢跨比增大，车站结构层间位移角整体呈降低趋势。因此大跨无柱车站进行结构设计时，应遵循“尽量起拱”的原则。

2.5 不同结构型式无柱车站的抗震横向相对位移分析

为对比不同结构型式下车站的抗震横向相对位移时程曲线，选取矢跨比具有代表性的平顶直墙结构和单圆拱结构进行对比，如图8所示。由图8可知，横向相对位移最大值位于车站的顶板处，最小值位于车站的底板处。随着矢跨比增加，结构的横向相对位移逐渐减少，抗震动力响应得到显著改善。

3 结语

本文针对不同结构型式的大跨无柱地铁车站，采用时程分析法进行了抗震动力响应计算，并对其结果进行对比分析，主要结论如下：

1) 在地层及竖向荷载作用下，部分竖向荷载通过拱形结构转化为轴力。相较于矩形平顶直墙结构，结构起拱后的弯矩值可减少约35%，结构顶板>处弯矩值得以明显改善，受力性能显著提升，具有较好的抗震特性。

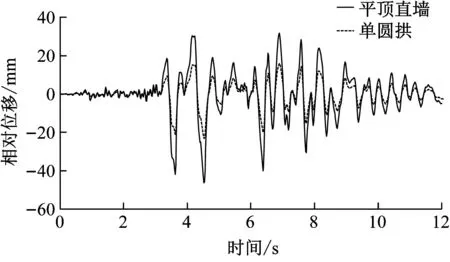
a) 顶板处

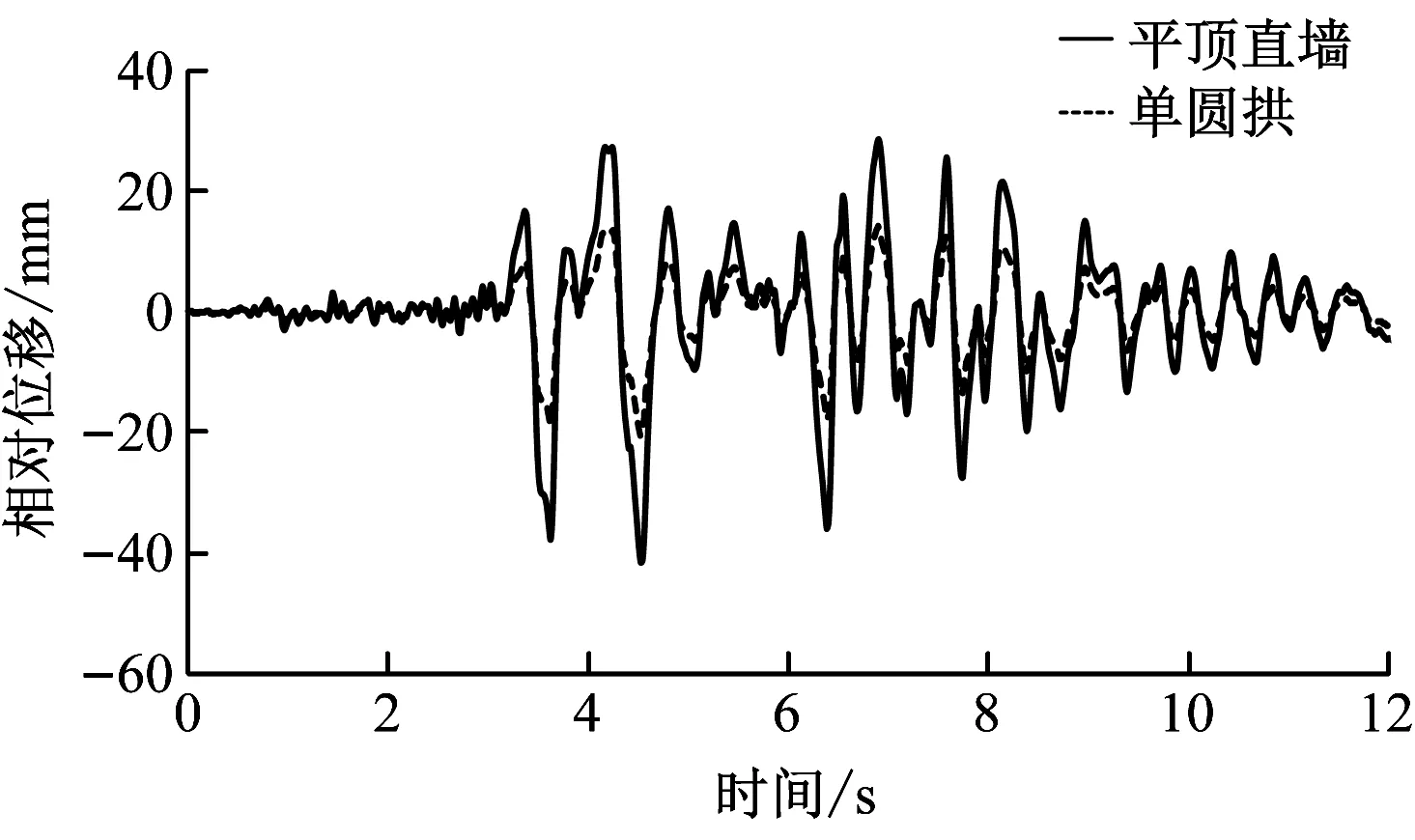
b)侧墙处

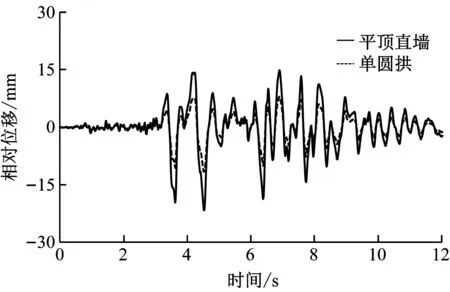
c)底板处

2) 对于拱形车站，拱顶不同矢跨比对结构内力及层间位移角影响的敏感性表明，随着结构矢跨比的增大，结构层间位移角整体呈递减趋势。其中，折线拱较平顶直墙结构降幅较大，曲拱较折线拱结构降幅较小。当矢跨比大于0.25时，层间位移角降幅逐渐趋于平缓。

3) 不同结构型式下车站的内力极值出现在板墙相交位置附近，该处为抗震薄弱点。相比框架结构地铁车站，大跨无柱车站缺少框架梁等主要耗能构件，因此在设计时应针对性地强化其抗震薄弱位置的抗震构造措施，以提高结构在地震作用下的抗剪和抗弯承载能力。

4) 考虑到车站内部结构及轨行区回填混凝土等有利荷载，车站底板设置仰拱方案相较车站顶板起拱方案，受力改善不明显。在卵石地层条件下，仰拱矢跨比为0.1时已能基本满足浅埋明挖无柱车站的底板受力需求。

对大跨无柱地铁车站的设计和施工提出建议如下：① 无柱地铁车站矢跨比的选择宜结合站内管线综合需求及建筑装修效果统筹考虑。在满足其他专业需求的条件下，顶板结构的选择宜趋于合理拱轴线。② 当无柱车站采用预制构件时，考虑到拼装节点位置及工艺与现浇混凝土车站不同，其结构抗震动力响应及抗震薄弱环节可能存在一定变化，因此可开展针对预制构件的结构抗震动力响应分析及选型研究。