基于剩余寿命可靠度的地铁车辆设备多部件趋近机会维修策略*
2021-03-22杨艳娟徐永能董瑞超
杨艳娟 徐永能 董瑞超
(南京理工大学自动化学院, 210094, 南京∥第一作者, 硕士研究生)
在保证列车安全性、可靠性的基础上如何减少维修费用,对车辆设备全寿命周期内的维修周期进行优化[1],对不同车辆部件实施统筹维修,成为现阶段一个值得深入研究的问题。学者们对城市轨道交通车辆的维修周期进行了深入研究,特别是以预防维修模式为出发点,考虑了关键部件的可靠性,优化维修周期模型[2-4]。本文主要是在对地铁车辆设备全寿命分析的基础上,建立以全寿命周期单位维修费用最小化为目标函数、以设备剩余寿命可靠度为约束条件的预防性维修周期模型,并对多部件整体维修提出趋近机会维修策略。
1 地铁车辆设备全寿命分析
本文将设备末次预防性维修后的时间纳入到设备全寿命范围内,利用地铁车辆设备大多服从威布尔分布这一特征,推导设备在末次预防性维修后的剩余寿命时间。
定义地铁车辆设备的可靠度函数为R(t),寿命分布函数为F(t),则R(t)的计算公式为:
R(t)=1-F(t)=P{X>t},t≥0
(1)
式中:
t——设备的运行时间;
P{X>t}——在规定条件下时刻t以前设备正常工作的概率。
对于服从威布尔分布的产品,其可靠度为:
R(t)=exp(-(t/η)β),(η,β>0)
(2)
式中:
η——尺度参数;
β——形状参数。
根据寿命期望值(MTTF)含义定义设备平均寿命为E(t),其计算公式为:
(3)
对于服从二参数威布尔分布的设备其剩余寿命函数μ(t)的计算公式为:
(4)
则设备的全寿命函数Tz可以表示为:
(5)
式中:
i——预防性维修的次数;
N——设备全寿命周期内的预防性维修总次数;
Ti——设备的第i次维修时距上次维修的时间间隔;
μ(t)——第N次预防性维修后设备的平均剩余寿命。
2 预防性维修周期优化模型
本模型在充分考虑车辆设备可靠性水平的基础上,建立了以单位时间维修费用最低为目标的预防性维修周期模型。
2.1 模型假设
由于地铁车辆设备是由多个部件组成,假定各部件均有以下几个性质:① 部件投入使用时是全新的;② 部件的故障率是独立的,遵循威布尔分布,且只考虑部件之间的维修周期与经济相关性;③ 预防性维修使部件的故障率下降到偶然故障阶段的故障率(即修复如新),但同时增大了故障率函数的变化率;④ 对于预防性维修周期内发生的故障只采取故障维修措施,不改变部件的故障率及其故障率函数;⑤ 部件可靠性随着役龄时间增加而下降。
2.2 剩余寿命可靠度约束
根据可靠性函数的含义,可以定义设备剩余寿命可靠性函数Rt(u)如下[5]:
(6)
式中:
Xt——设备已服役时间t后的剩余寿命时间。即:设备在t时刻进行了一次上述规定的预防性维修后,再经过时间u,在时刻t+u正常工作的概率。
当设定剩余寿命可靠度应大于或等于某一阈值α时,Rt(u)可在式(6)的基础上表示为:
(7)
式中:
α——剩余寿命可靠度阈值。
求解上述方程,可求得u的值。当设备寿命服从二参数威布尔分布时,预防性维修周期的求解方程为:
(8)
式中:
TN——待求的下一次维修周期。
2.3 预防性维修周期的确定
在地铁车辆设备的全寿命服役期间,其总维修费用CZ主要由五部分组成:预防性维修费用C1、在预防性维修周期内出现的故障维修费用C2、因进行预防性维修而造成的损失C3、因进行故障维修而造成的损失C4和在拆卸故障部件时造成的间接损失费用C5。总维修费用及其组成费用的计算公式为:
CZ=C1+C2+C3+C4+C5
(9)
(10)
C2=CemF
(11)
(12)
(13)
C5=CwF
(14)
式中:
Cep——每次预防性维修的费用;
φ——故障率递增因子;
ti——第i次预防性维修所花费的时间;
Cem——预防性维修周期内每次故障维修的费用;
F——设备全寿命周期内预期发生的故障维修总次数;
Cl——因预防性维修而使设备停用造成的单位时间损失;
Cq——因故障维修而使设备停用造成的单位时间损失;
tj——第j次故障维修所花费的时间;
Cw——因故障维修而拆卸故障部件造成的间接经济损失,最主要的包括拆卸费用。
其中,Cl、Cq和Cw根据经验法取其理想情况,假设每次造成的经济损失为一固定值。
(15)
混合式故障率需要考虑综合役龄递减因子ω和故障率递增因子φ两种因子,在每次预防维修后设备故障率减小到维修前的某一水平,然后以更快的速度增长[6]。这两个参数取文献[6]所取数值。根据混合式故障率函数的递推关系,可以得第i次预防维修周期内的故障率λi(t)为:
λi(t)=φλi-1(t+ωTi-1)
(16)
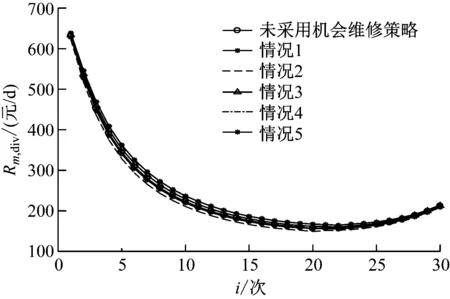
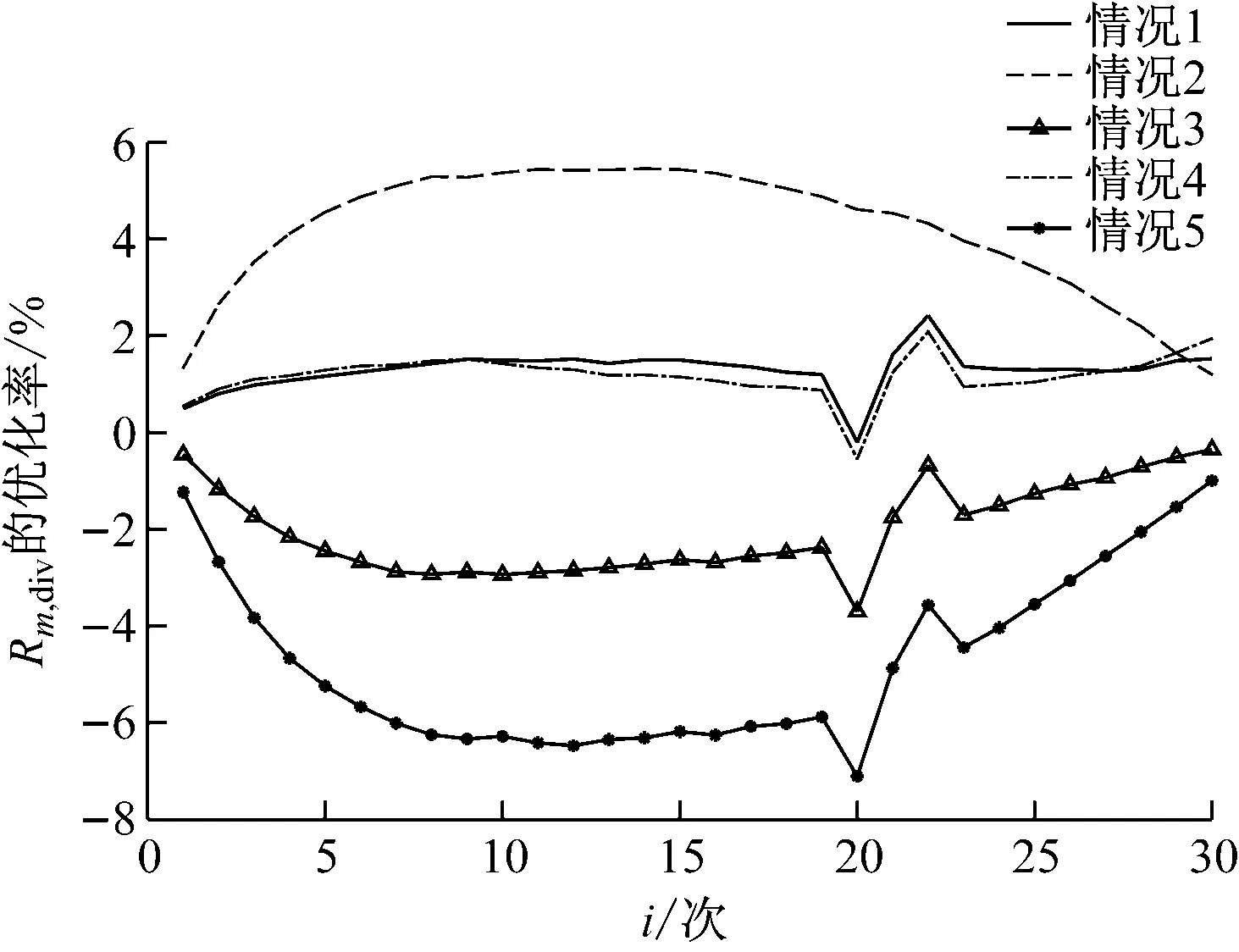
其中,i=1,2,…,N;0 式中: λi(t)——第i次预防性维修周期内的故障率。 机会维修策略的特点是可以整合多个部件,对于具有相同维修间隔的两个或多个部件,进行整体维修。但是,这种维修策略必须建立在各部件维修时间已经确定的基础上[7]。 本文的策略是在建立预防性维修周期的同时,考虑机会维修的策略,将机会维修的“被动性”转变为“主动性”。趋近机会维修策略具体流程如下: 步骤1:计算不同α情况下各部件相关函数,改变剩余寿命可靠度约束的阈值α,可以得到不同α值的各部件预防性维修周期Tb(i)、全寿命周期平均费用Rb(i)和已运行时间Tb,add(i)。其中:参数b表示相应的部件(b=1,2,…,S),S表示设备的部件总数。 步骤2:选取各部件的初始相关函数,根据专家系统法,得到部件b的初始α以及允许的阈值改变绝对值Δα。计算初始α情况下的Tb(i)、Rb(i)、Tb,add(i),所得结果分别作为最优维修周期Tb,best(i)、最优全寿命周期平均费用Rb,best(i)和每个部件的最优已运行时间Tb,add_best(i)。 步骤3:初始化m=1,m表示第m个方案(m=1,2,…,S),即趋近第m个部件维修周期时进行整体维修的情况。 步骤4:初始化i=1。 步骤5:选择情况m下的最优相关参数,即Tm,best(i)、Rm,best(i)和Tm,add_best(i)。 步骤6:初始化z=min(Z),Z为不包含第m个部件的其他部件的集合(z表示第z个部件的维修周期趋近部件m的维修周期,用来判断其余S-1个部件是否趋近m情况)。 步骤7:计算当前的维修周期,根据Δα计算Tz,αmin(i)和Tz,αmax(i),计算Tm,addbest(i)和Tz,add(i-1)的差值得到Tz,m(i)。其中,Tz,m(i)表示部件z在方案m的情况下第i次维修,判断Ti,(z,m)是否位于Tz,αmin(i)和Tz,αmax(i)之间,如果满足要求,则Tz,m(i)正确;否则判断Tz,m(i)与Tz,αmin(i)和Tz,αmax(i)之间的欧几里得距离,选择欧几里德距离最小值。 步骤8:判断z是否等于集合Z中最后一个部件。如果满足,进行下一步;否则,z指向集合Z中的下一个部件,返回步骤7。 步骤9:判断i是否为最大维修次数。如果满足要求,则进行下一步;否则i=i+1,执行步骤5。 步骤10:计算方案m下的Rm,div(i)(Rm,div(i)为将所有部件看作整体考虑时机会维修的平均费用)。 步骤11:判断m是否满足全部情况。如果是,执行下一步;否则m=m+1,执行步骤4。 步骤12:选择Rm,div(i)的最小值为最优结果。 以地铁车辆转向架的轴承、轮对、轴箱、减震装置、抗侧滚扭杆等5个关键部件[8]为例,将部件分别编号为1#、2#、3#、4#、5#,构成一个串联结构,各部件服从威布尔分布的具体参数如表1所示。本算例仅考虑理想情况,转向架各部件的故障率服从威布尔分布,且各部件均以全新的状态运行。部件的相关单位维修费用均采用平均值,设Cep为1 500元/次、Cem为2 000元/次、Cl为1 500元/d、Cq为750元/d、Cw为600元/次。 表1 地铁车辆转向架各部件维修参数 采用剩余寿命可靠度方法,计算部件b的预防性维修周期Tb(i)、全寿命周期平均维修费用Rb(i)。以部件1#为例,其仿真结果如图1所示,图中Tb(i)表示部件1#第i次的预防性维修周期,Rb(i)表示部件1#前i次的全寿命周期平均维修费用。 a)预防性维修周期 b)全寿命周期平均维修费用 从图1 a)可以看出,在α值固定的情况下,部件1#的预防性维修周期Tb(i)随着维修次数i的增加而降低,并且Tb(i)降低的速率也随着维修次数i的增加而降低;在i相同的情况下,部件1#的Tb(i)随着α的增加而降低,降低的速率基本维持在某一固定值;从图1 b)可以看出,在α值固定的情况下,部件1#的全寿命周期平均维修费用Rb(i)随着维修次数i的增加呈现先减少后增加的趋势,Rb(i)的最小值对应的维修次数即为部件1#的最佳维修次数Nb,best(i);在α值由小变大的过程中,i相同的情况下Rb(i)在逐渐增大,但是部件1#的最佳维修次数也在增加。 仿真发现,部件2#~5#的特征与部件1#相似,这里就不再赘述。在部件b初始α值的选取上,本文采用专家系统法,将Rb(i)和Nb,best(i)的权重各设为0.5,从而得到的初始α值为0.85。 根据专家系统法,选取各部件允许的维修策略α值的变换范围。基于初始α值为0.85,本文选择α值的范围为[0.83,0.87]。当初始α值为0.85时,转向架各部件的仿真结果如图2所示。 图2 各部件的全寿命周期平均维修费用(α=0.85时) 从图2可以看出,当5个部件互不相关时,其Rb(i)可满足实际要求。而在实际维修过程中,通常把相关的部件看作一个整体,在计算多部件整体的全寿命周期平均费用Rm,div(i)时,通常考虑机会维修策略。本文对该转向架采用趋近机会维修策略进行整体维修,将趋近第m个部件维修周期进行整体维修的情况,表示为第m个方案,看作情况m,例如情况1表示,部件2#、部件3#、部件4#、部件5#趋向部件1#维修周期的情况,分别趋近于部件1#、部件2#、部件3#、部件4#、部件5#等5种情况的多部件整体全寿命周期平均维修费用Rm,div(i),如图3所示。 图3 不同情况的趋近机会维修策略的全寿命周期平均维修费用(α=0.85) 将每种情况得到的全寿命周期平均费用与不采用机会维修策略进行对比分析,计算出不同情况的优化结果如图4所示。 图4 全寿命周期平均维修费用的优化率结果 从图4可以看出: 1) 情况1和情况4相比于不采用机会维修策略的优化结果相似。当N达到22或23时,得到的最大优化率为2%左右。在设备整体的最佳维修次数Nbest为20时,情况1和情况4基本没有优化; 2) 情况2所对应的Rm,div(i)优化最大,其优化率随着维修次数呈现先增后减的趋势:在N达到15时,其优化率达到最高,约为5%;当Nbest为20时,情况2的优化率在4%左右; 3) 情况3和5相比于不采用机会维修策略费用有所上升。当维修次数达到Nbest为20时,情况5多消耗了约7%的费用的,情况3多消耗了约4%的费用。 通过上述结果可以看出,情况2的优化效果最好,在Nbest为20时,优化率高达4%左右,即全寿命周期平均费用降低了约4%。因此,对地铁车辆的多部件采用趋近机会维修策略,可在保证其安全可靠性的基础上,减少全寿命周期平均费用,提高维修效率。 在城市轨道交通车辆设备制定维修计划时,选择科学合理的维修策略可以帮助运营公司节约时间与成本。本文基于剩余寿命可靠度,建立了地铁车辆设备的预防性维修周期模型,并针对多部件维修提出了趋近机会维修策略。通过算例仿真可以看出,该预防性维修周期模型能得到合理的部件维修周期,选择合适的趋近情况可以降低多部件整体全寿命周期的单位时间维修费用,其费用优化率最高可达5%,从而验证了趋近机会维修策略的合理性和有效性。3 地铁车辆的多部件趋近机会维修策略
4 算例分析
4.1 设置车辆转向架的关键部件参数
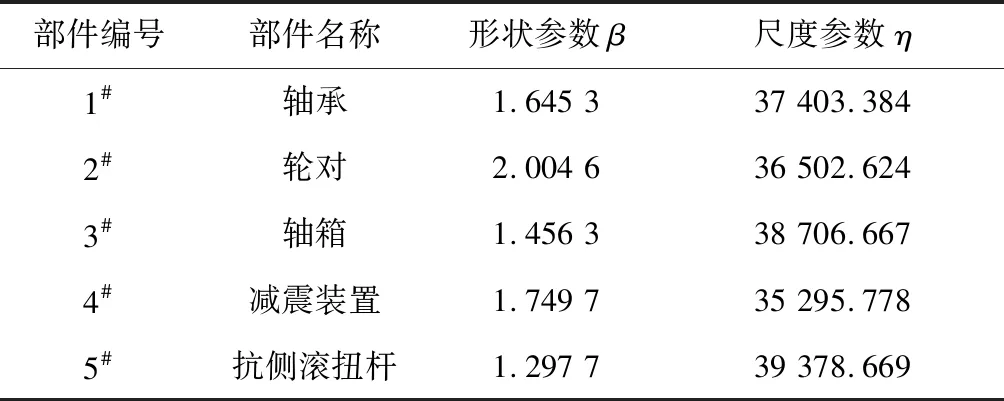
4.2 确定各部件预防性维修周期的初始α值
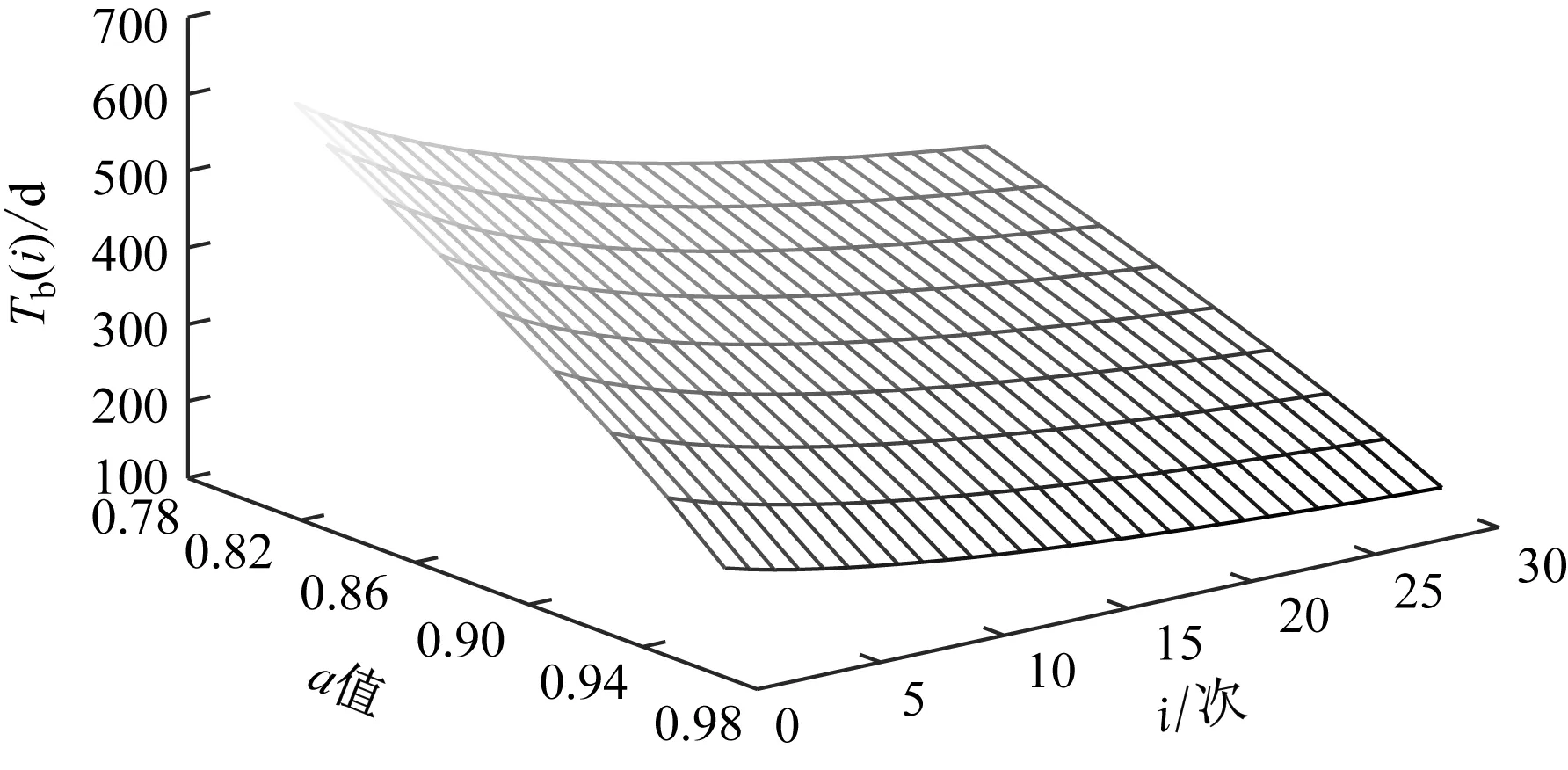
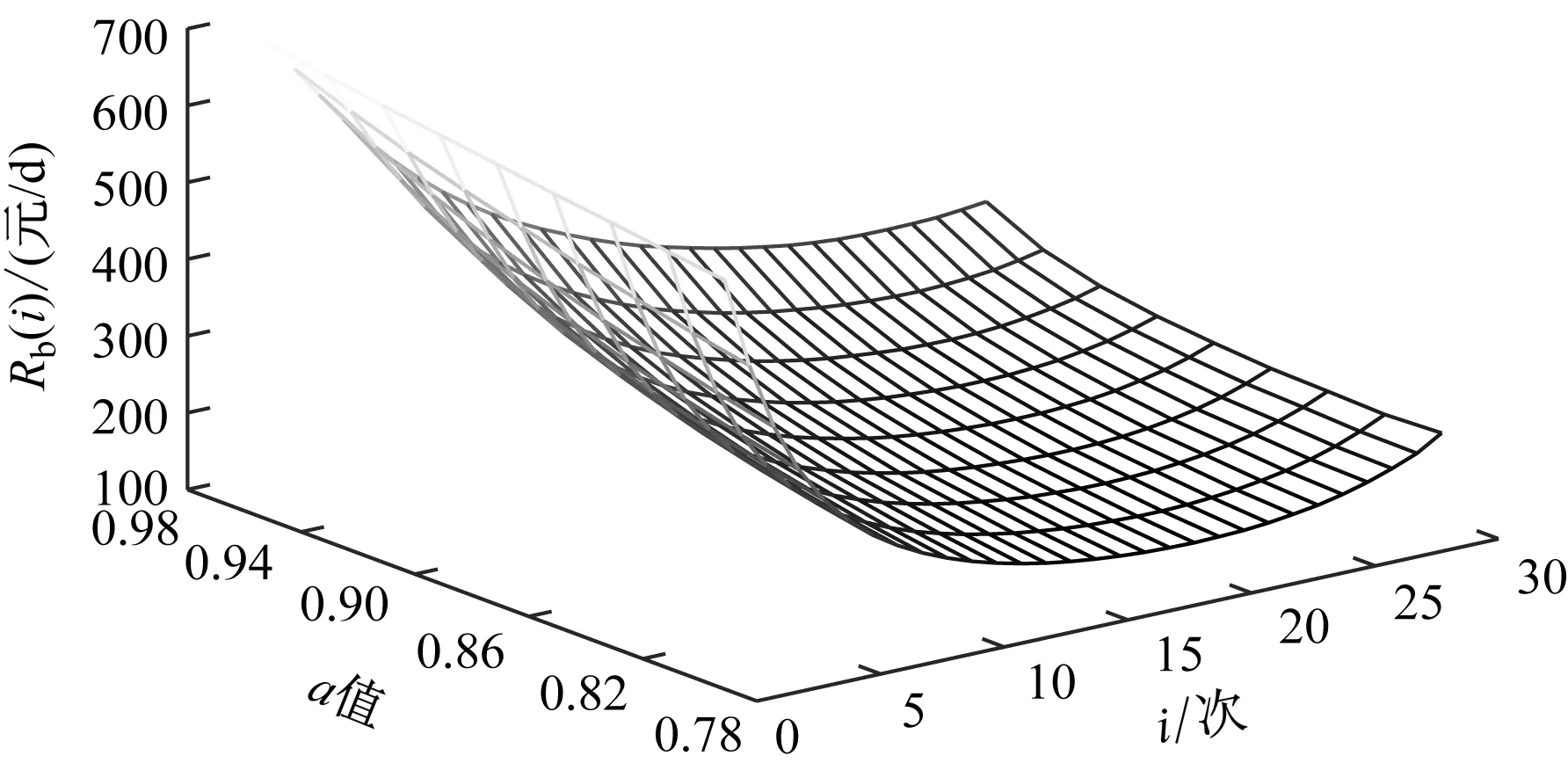
4.3 转向架各部件趋近机会维修策略仿真
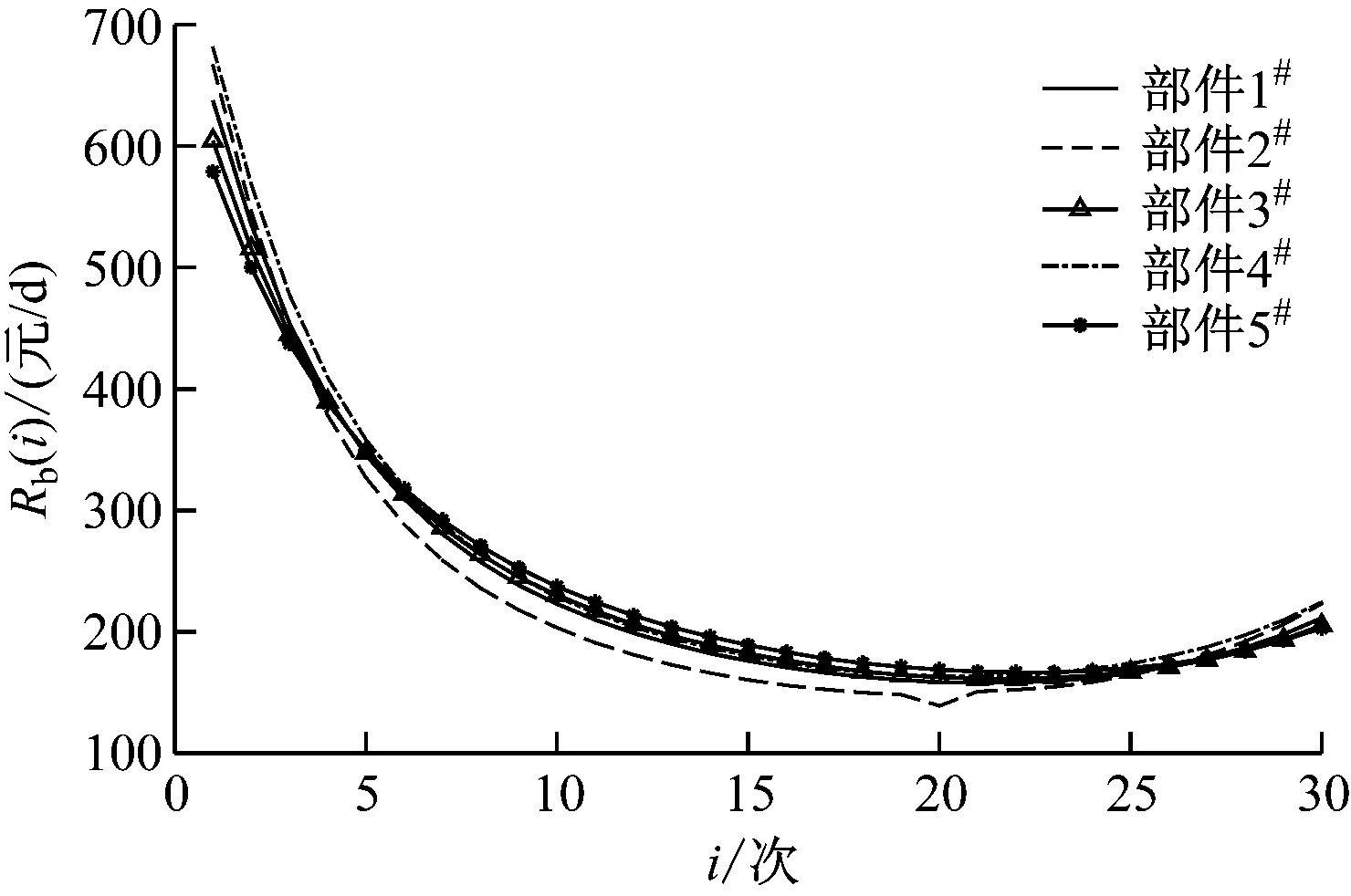
5 结语
