平均发展速度概念及误区分析
2021-03-22王贵虎
王贵虎
(工业和信息化部电子第五研究所, 广东 广州 510610)
0 引言
个人和企业在年度总结或做经济分析的时候,通常用发展速度来说明成绩或实际现状, 尤其是对一段时间或比较长一段时间通常用平均发展速度来做描述发展的概括, 但很多人在使用这个概念时通常存在误区, 本文结合实例介绍和分析了关于动态发展速度存在的误区。
1 发展速度的几个概念
发展速度是说明报告期水平已发展到基期水平的若干倍或百分之几, 它是根据两个不同时期发展水平对比而得到的, 用倍数或百分数表示。发展速度由于对比的基期不同可分为环比发展速度和定基发展速度。
1.1 环比发展速度
环比发展速度是指报告期水平与前一期水平之比, 其说明的是某一现象较前一期发展的程度。
环比发展速度=ai/ai-1
1.2 定基发展速度
定基发展速度是指报告期水平与某一固定时期水平(通常为最初水平) 之比, 其说明的是现象在较长时期内总的发展速度, 因此又称“总速度”。
定基发展速度=ai/a0
1.3 两种发展速度的关系
a) 定基发展速度等于相应各个环比发展速度的连乘积。
b) 相邻两个定基发展速度之比等于后一期的环比发展速度。
2 增长速度的几个概念
增长速度是说明报告期水平比基期水平增长了若干倍或百分之几, 它是增长量与基期水平之比, 用倍数或百分数表示。
增长速度=发展速度-1 (或100%), 当发展速度大于1, 增长速度为正值, 称为增长率; 当发展速度小于1, 增长速度为负值, 称为降低率。 增长速度由于对比的基期不同可分为环比增长速度和定基增长速度。
2.1 环比增长速度
环比增长速度是逐期增长量与前一期水平之比。
环比增长速度=环比发展速度-1 (或100%)。
2.2 定基增长速度
定基增长速度是累计增长量与某一固定时期水平之比, 其表明的是某种现象在较长时期内总的增长速度。
定基增长速度=定基发展速度-1 (或100%)。
2.3 增长速度与发展速度关系的实例分析
已知某厂的产量2 007 年比2001 年增长了120%, 2008 年比2001 年增长了175%, 请计算2008 年比2007 年增长多少?
由于a07/a01=1+120%, a08/a01=1+175%, a08/a07=(a08/a01) /(a07/a01) =2.75/2.2=125%, 由此可知发展速度为125%, 增长速度为25%。
3 平均发展速度
平均发展速度是各个时期环比发展速度的序时平均数, 它说明的是某种现象在一个较长时期内逐期发展的平均程度[1-3]。 计算平均发展速度有着重要的实际意义, 通过它可以比较和说明某种现象在各个时期中的一般发展情况。
3.1 误区
平均发展速度很容易被理解为先分别求出各期的发展速度, 然后对各期的数据求算数平均值或加权平均值。 其实平均发展速度的计算按应用场合的不同分为几何法和方程法[4-5]。
3.2 几何法
几何法侧重于考察现象在一段时间内最后一期达到的水平。 其实质是从最初的水平a0出发,每期按照相同的速度(x) 发展, 经过n 期后, 便可达到最末水平an。 即an=a0xn, 此法成为“水平法”, 它适用于如产品产量、 社会商品零售额、 人口和工资等非累积指标计算。
如果现象发展的过程分为几个时期(阶段),同时又具备各个时期(阶段) 的平均发展速度指标, 要求全过程的平均发展速度, 则要以各个时期(间隔数) 为权数, 按加权几何平均数计算。例如: 某厂利润2010-2013 年平均增长18%,2014 年比2013 年增长17%, 2015-2020 年平均增长16%, 如何计算从2010 年到2020 年利润平均增长多少? 应该为[(1+18%)3× (1+17%) × (1+16%)6]1/10=118.5%, 即年均增长18.5%, 而不是(18%×3+17%+16%×6) /10=17.7%。
3.3 方程式法
方程式法侧重于考察现象在整个研究时期发展水平达到的累计数。 其实质是从最初水平a0出发, 每期按照相同的速度(x) 发展, 各期计算水平之和等于各期实际水平之和。 适用于基建投资额、 造林面积和新增固定资产投资额等累计性指标。 设a0, a1, a2, ……an-1, an是各期水平。 a1/a0=M1, a2/a1=M2……an/an-1=Mn, a1=a0M1a2=a1M2=a0M1M2……an=an-1Mn=a0M1M2…Mn, 用平均发展速度(x) 代替各期环比发展速度得出: a1=a0x a2=a1x=a0x2……an=a0xn, 因此各期发展水平之和为a0(xn+xn-1+…+x2+x1)。 因此得到以下方程式:
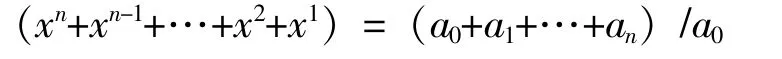
用计算机解以上方程便可求出平均发展速度,也可用查表法得出平均增长速度。 例如: 某地区2015-2020 年原油产量如表1 所示。

表1 原油产量单位: 万吨
采用方程式法计算年平均发展速度的步骤如下所述。
a) 判断增减
(a1+a2+a3+a4+a5) /5>a0为递增, 通过计算可得(a1+a2+a3+a4+a5) /5=8 370.2, 其中8 370.2>6 122,因此判定是增长。
b) 计算总的发展速度
(a1+a2+a3+a4+a5) /a0= (6 755+7 539+8 395+9 281+9 861) /6 122=683.62%
c) 解方程或查表可得平均增长速度为10.6%,发展速度为110.6%。
4 结束语
在写年度总结或现象分析的过程中, 要针对统计指标的特性, 选择合适的方法来计算发展速度和增长速度, 使得计算或分析更加科学、 可靠和可信, 给有关人员或上级决策辅助更精准。
