一类带有时滞脉冲的分数阶微分方程解的存在唯一性

周东鹏，周 霞

（桂林电子科技大学 数学与计算科学学院，广西 桂林541004）

分数阶微分方程在药物动力学、电磁学、控制论、多孔介质等[1-6]科学领域能更好地对系统的动力学行为进行建模。因此分数阶动力系统的研究在最近的几十年里受到了广泛地关注[7-15]。一般而言，需要对系统的解的研究，首先研究的问题是解的存在唯一性问题。关于分数阶脉冲微分方程解的存在唯一性问题已有报道：Wang 等[16]利用Banach 不动点定理得到了Hadamard 型导数的脉冲微分方程解存在性条件；Chalishajar 等[17]研究了一类分数阶脉冲积分微分方程解的存在性问题；Liu[18]利用迭代方法得到了脉冲分数阶柯西问题解的存在唯一性条件；Wu 等[19]通过分段函数给出了一类脉冲分数阶微分方程的精确解；李耀红等[20]利用Leray-Schauder 不动点研究了一类Caputo分数阶脉冲微分方程柯西问题解的存在性。已有文献所研究系统的脉冲是不含时滞的，然而在实际应用中，发生突变时刻的系统状态不仅与当前时刻有关还与过去时刻有关。因此，本文考虑脉冲时刻含有时滞的情况，研究带有时滞脉冲的分数阶微分方程解的存在唯一性。

考虑带有时滞脉冲分数阶非线性微分方程：

1 预备知识

符号说明：Z+表示一切正整数的集合，N 表示一切自然数的集合，Rn表示n 维实数空间。

定义1[21]函数 f:[0,T]×Rn→Rn的a＞0 阶Riemann-Liouville 分数阶积分定义为

其中算子Ja是满足半群性质的，即存在a，b＞0 使得JaJbf(t,x(t))=Ja+bf(t,x(t))。

定义2[21]函数x(t) 的0 ＜a ＜1 阶Caputo 阶分数阶积分为

为了得到方程(1)解的存在唯一性条件，假设如下条件成立。

(H1)函数f:[0,T]×Rn→Rn和I:Rn→Rn满足Lipschitz 条件，即存在非负常数L1和L2使得如下不等式成立:

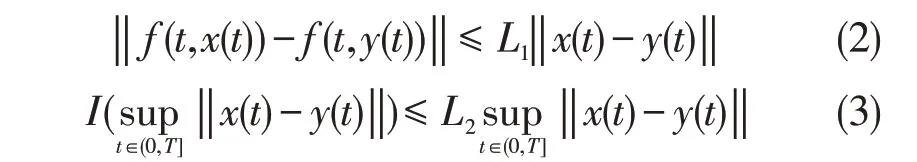
(H2)脉冲函数I:Rn→Rn是线性映射，即存在常数a 和b 使得

定理1 若(H1)，(H2)成立，并且存在非负常数L1,L2,T,τ 使得

成立，则方程(1)的解存在且唯一。

显然π 在每个t ∈(tk，tk+1]，k ∈N 区间上都是连续算子。下面分区间来讨论。由上式和(H1)可得，当t ∈(0，t1]时，

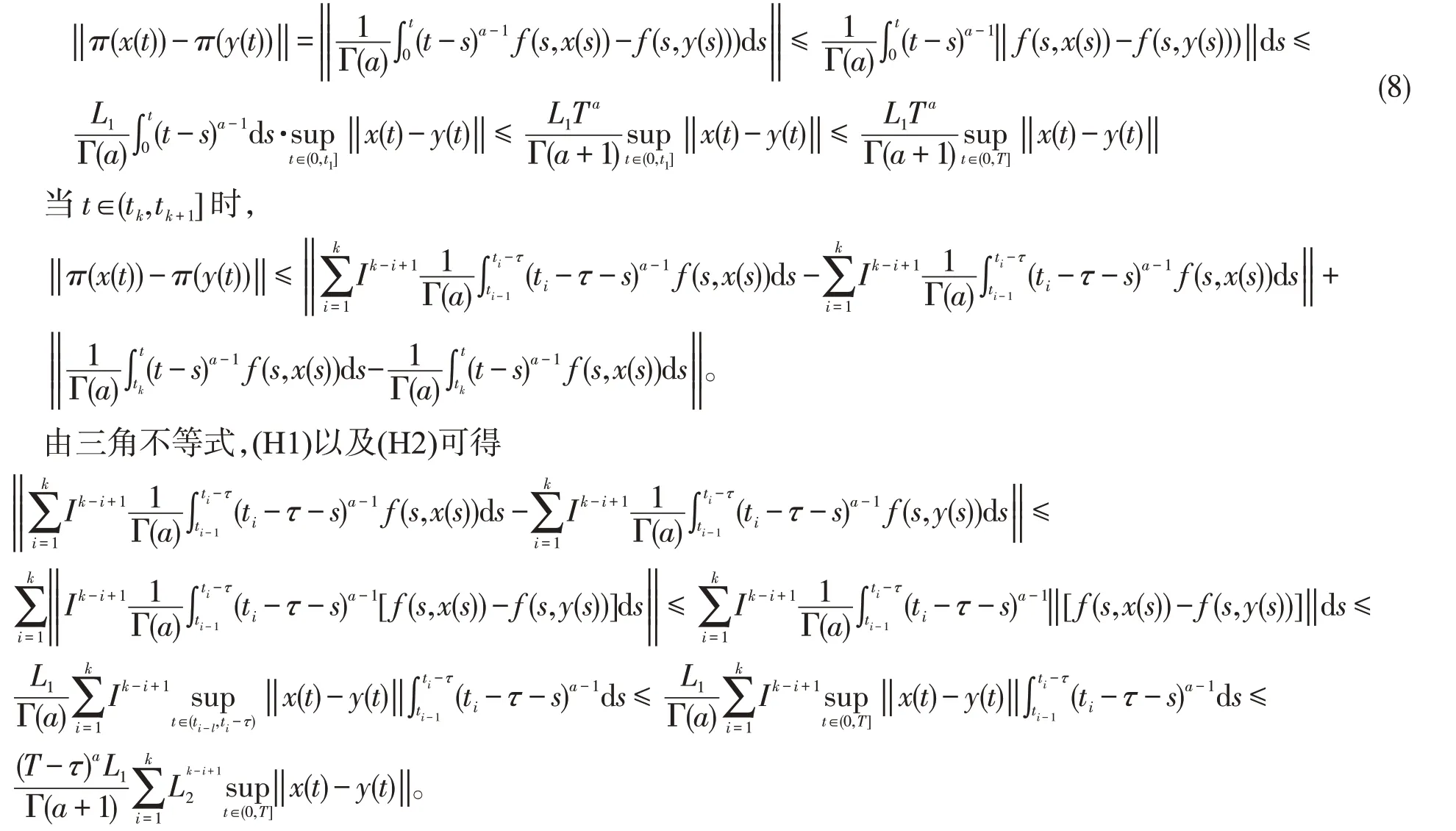
同理可得

结合不等式(5)，(6)，(8)以及Banach 不动点定理可知，对任意的k ∈N，方程(1)的解存在且唯一。

当方程(1)中的时滞项τ=0 时，方程(1)退化为如下不含时滞的脉冲分数阶微分方程：

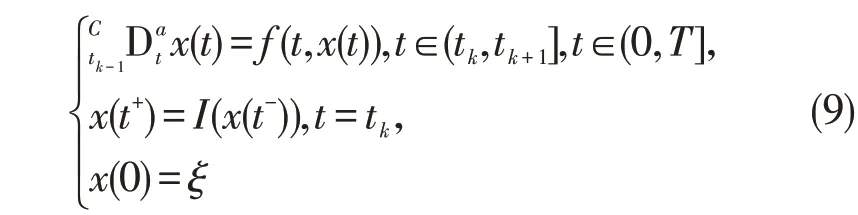
推论1 假设(H1)，(H2)成立，若存在非负常数L1,L2,T 使得

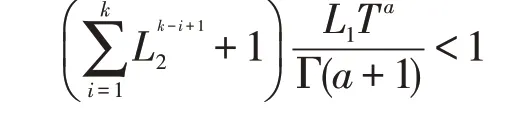
成立，则方程(9)的解存在且唯一。

注1 在文献[20]中，李耀红等利用Leray-Schauder 不动点研究系统(9)解的存在性问题，注意到该系统是本文τ=0 时的一种特殊情形，因此从这一方面而言，本文的结果更具有一般性。

2 数值实例

图1 系统(10)的数值解

3 小结

本文利用Banach 不动点定理，研究了一类带有时滞脉冲的分数阶微分方程解的存在唯一性问题，得到了对应柯西问题解存在唯一性的充分条件。与文献[16-20]相比，本文考虑的脉冲是带有时滞的，并本文结果可以推广到脉冲时滞为0 的情形或者脉冲项为0 的情形。同时，本文条件更具有一般性，因此应用范围也更加广泛。